基于道路行駛工況辨識的重型載貨汽車排氣制動系統主動控制研究*

史培龍，趙 軒，陳子童，余 強

（1.長安大學汽車學院，西安 710064；2.北京理工大學機械與車輛學院，北京 100081）

前言

為降低行車制動系統在下坡路段的熱負荷，不依賴于摩擦制動的發動機制動、排氣制動和緩速器制動廣泛應用于商用車中，但是因為駕駛人路況不熟悉和經驗不夠豐富等因素未及時開啟排氣制動、緩速器制動引發制動器熱衰退造成的重特大交通事故時有發生，因此載貨汽車制動安全問題一直是熱門話題。

近年來，關于制動控制研究多集中在新能源汽車領域，純電動汽車充分利用電機制動回收制動能量而增加續駛里程，大多采用制動意圖辨識的策略［1-4］；混合動力汽車針對電機制動力不足的問題，利用電機制動、發動機制動、摩擦制動協調控制策略，實現提高制動安全和經濟性的雙重目的［5-10］。商用車方面，許世維等［11］以制動踏板位移和制動踏板位移變化率為輸入設計了制動意圖的模糊推理規則，并建立了基于LQV 神經模糊系統的制動意圖識別模型，在制動力分配要求、電機再生制動約束、蓄電池約束等條件下研究了機-電復合制動控制策略，但是僅考慮了單次制動工況和中國典型城市公交工況（CCBC工況）；韓云武等［12］提出一種滿足駕駛人主觀意圖、確保下坡安全性和提高制動能量回收性能的混合動力汽車下坡輔助控制方法，研究了下坡輔助控制啟動與退出策略、電機單獨制動、電機-發動機聯合制動和電機-發動機-液壓聯合制動的轉矩分配策略；韓云武等［13］針對下坡工況下混合動力汽車輔助制動控制退出過程中的安全隱患提出了基于駕駛員主觀意圖和行車安全的輔助制動退出控制方法。

傳統的燃油商用車方面，馬建等［14］為了縮短制動距離提出了基于神經網絡的緩速器停車距離控制系統；余強等［15］為了解決發動機制動力不足的問題，提出了發動機制動與緩行器聯合作用的持續制動方式，有效地減少汽車連續下坡行駛時由于主制動器過熱而造成的交通事故；張焱等［16］研究了緩速器不同擋位制動力利用率與路面附著系數的關系，提出盡量避免緩速器長時間工作于最高擋進行下坡制動控制；趙迎生等［17］建立了汽車下坡的動力學模型和主制動器與電渦流緩速器的熱力學模型，利用制動力模糊分配器控制緩速器和行車制動器之間動態分配關系改善緩速器的制動熱負荷；趙迎生等［18］通過建立聯合制動系統制動力分配的優化模型獲得制動力分配系數與道路坡度的函數關系，從而對緩速器和行車制動器進行動態控制。上述關于電動汽車和混合電動汽車研究的文獻中，目前主要集中在制動能量回收和電機制動與傳統制動系統之間的動態協調控制問題，傳統的控制系統需要手動啟動而高度依賴駕駛經驗和技能，未考慮駕駛人山區路段的制動行為特性。

輔助制動系統在商用車領域應用較為廣泛，但是由于駕駛人經驗不足和路況不熟而引發的制動安全事故時有發生，因此本文對排氣制動系統的主動啟動和退出控制策略進行研究。依據車輛控制器局域網絡中的制動踏板開度和加速踏板參數，在線辨識車輛行駛工況，主動控制排氣制動系統開啟和關閉。該方法不需要增加額外傳感器，利用車輛CAN總線數據，經車輛控制單元運算后給排氣制動系統發送信號進行開啟和關閉，主動控制輔助制動系統而降低行車制動系統熱負荷，避免因駕駛人錯誤操作而引發制動安全事故，降低了駕駛人的疲勞強度，提高了重型載貨汽車下坡路段行駛安全性。

1 行駛工況建模與辨識

1.1 行駛工況特征參數

為了建立下坡路段行駛工況模型，文中以六軸半掛汽車為研究對象，選取京昆高速雅安-西昌段K25-K174 左線和右線駕駛人自由駕駛車輛試驗數據進行建模分析。該路段總長298 km，垂直落差將近1 600 m，最大縱向坡度5%，大于2%縱向坡度道路占比58.14%，大于3% 縱向坡度道路占比27.49%，屬于典型的山區長大下坡路段。

經統計分析，車輛在京昆高速雅安-西昌段K25-K174 左線和右線行駛過程中采取行車制動次數達461 次，制動器作用總時間為6 569.3 s，占行駛總時間的35.36%，平均每次制動時間為14 s，具體見表1。由此可見，山區長下坡路段行駛的重型載貨汽車制動踏板作用時間及比例明顯高于其他路段。

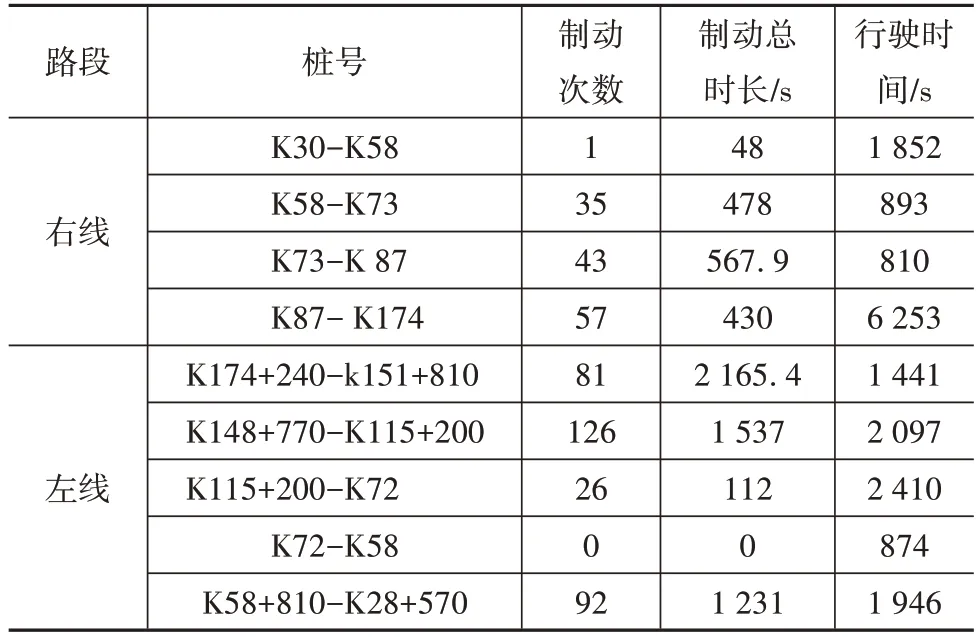
表1 長下坡路段制動數據統計

為了描述制動踏板在一定時間段內的動作行為，文中引入了時間窗T，用時間窗內的制動踏板平均開度、制動踏板作用時間和制動踏板作用比例pi為特征參數構建行駛工況。如式（1）～式（3）所示。

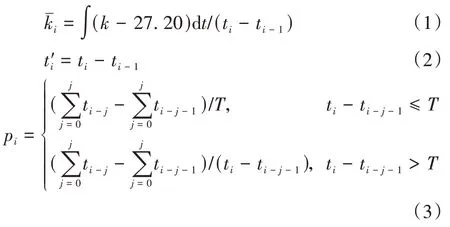
式中：k為制動踏板開度；ti和ti-1為兩次制動相鄰時刻；ti-j和ti-j-1為第j個時間窗制動相鄰時刻。

1.2 隱馬爾可夫模型

考慮駕駛人制動行為和道路特征的因果關系，且具有一定時間歷程，因此利用時間尺度建立行駛工況識別的隱馬爾可夫模型，特征參數選取時間窗內的制動踏板平均開度、制動踏板作用時間和制動踏板作用比例pi。

根據馬爾可夫狀態識別前向-后向算法，前向向量α(t，j)和后向向量β(t，j)的迭代如式（4）和式（5）所示。

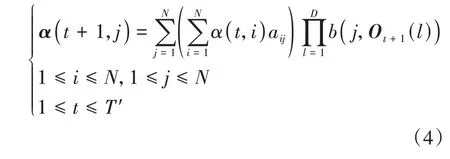
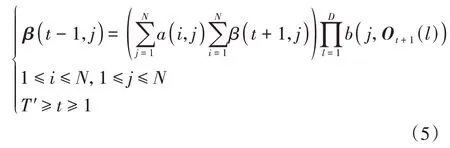
式中：Ot(l)為第t個觀測序列的多因素觀測矩陣，長度為D；T′為觀測矩陣的長度；b(j，Ot(l))為j狀態時刻在狀態Qt的出現概率，根據l的取值范圍可以將b(j，Ot(l))分成D個狀態矩陣B1，B2，...，BD，分別表示隱含狀態下出現不同觀測對象的概率矩陣。

隱含狀態到觀測值狀態的概率矩陣［19］為

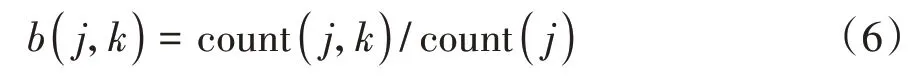
式中：count(j)為觀測序列中狀態j出現的次數；count(j，k)表示在一個觀測類中j狀態下出現觀測值k的次數。

多維馬爾科夫模型不能直接應用于隨時間連續變化的量，觀測序列表述需要用多個高斯函數組成的混合高斯模型的輸出概率來表示。每一種隱含狀態都用一個混合高斯模型來描述，通過不同的權重高斯函數組成混合高斯模型。觀察值概率矩陣B是混合高斯模型輸出觀測序列的概率。此時模型的概率密度函數可表示為

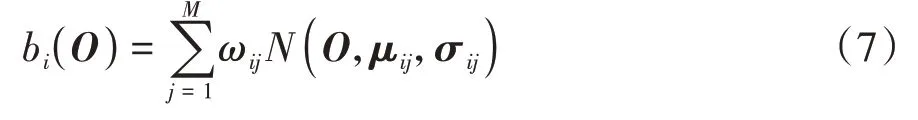
式中N(O，μij，σij)表示在狀態i中第j維高斯概率密度函數。

假設εt(i，j)為狀態t時刻狀態i觀測序列中第j個混合高斯函數的概率，則時刻t馬爾可夫鏈處于狀態i而時刻t+1處于狀態j的概率如式（8）所示。

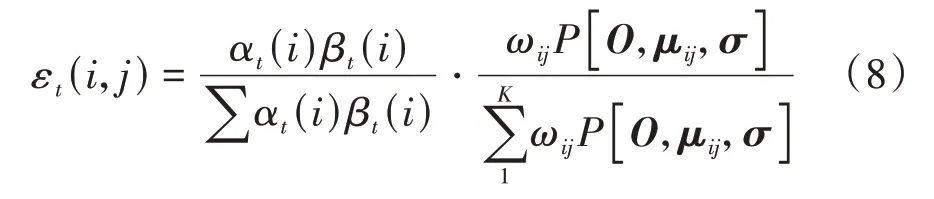
式中：μij為混合高斯函數的均值矩陣；σ為不同識別參數和不同高斯函數的混合協方差矩陣；ωij為不同混合高斯函數輸出概率的權重。

根據混合高斯模型對馬爾科夫混合高斯參數重估，如式（9）～式（11）所示。

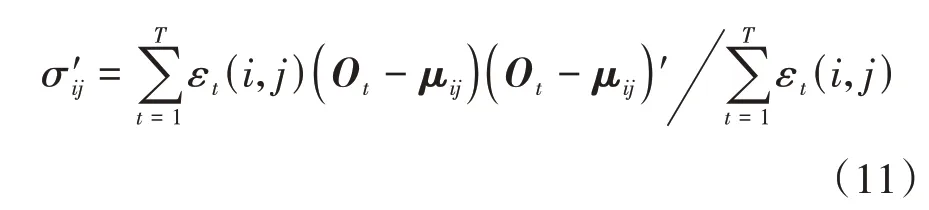
依據確定特征參數，觀測序列可表示為

1.3 模型訓練及辨識驗證

考慮到用最大值或平均值不能準確描述山區路段下坡制動動作行為，為此，文中采用時間窗分割法［20］，如圖1 所示。首先將采集參數劃分成時間窗片段，其次對每個片段內參數均值進行離散化處理［21］，最后獲得基于時間窗的連續變化序列數。為了研究不同時間窗長度對識別效果的影響，文中時間窗長度T分別設置為30、60、90和120 s。

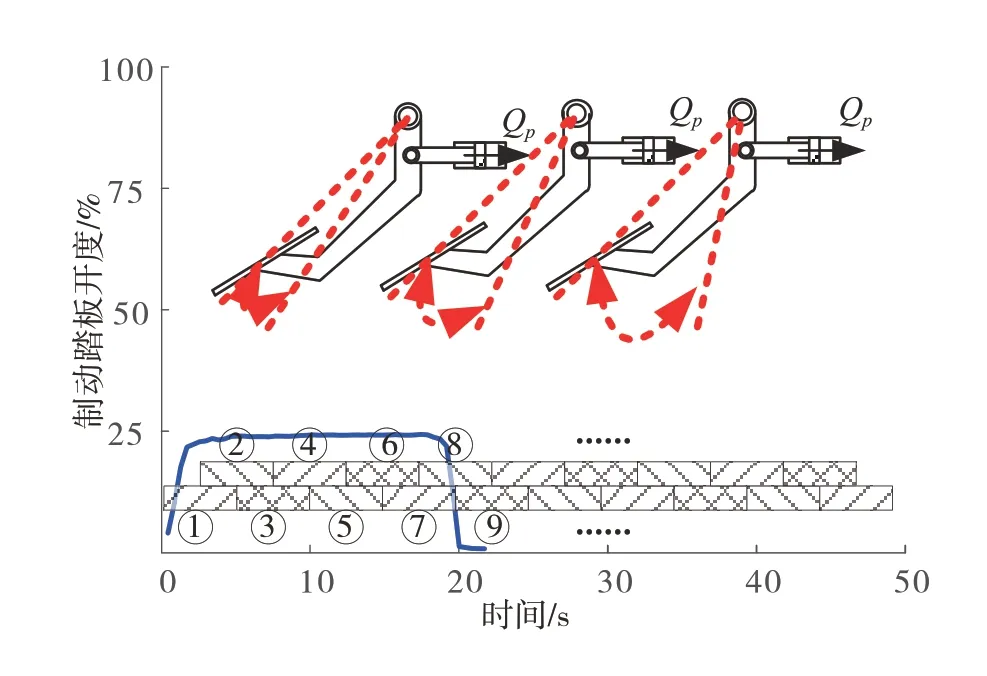
圖1 時間窗分割示意圖

依據道路特征提取長下坡道路和一般道路制動踏板動作數據，見圖2。

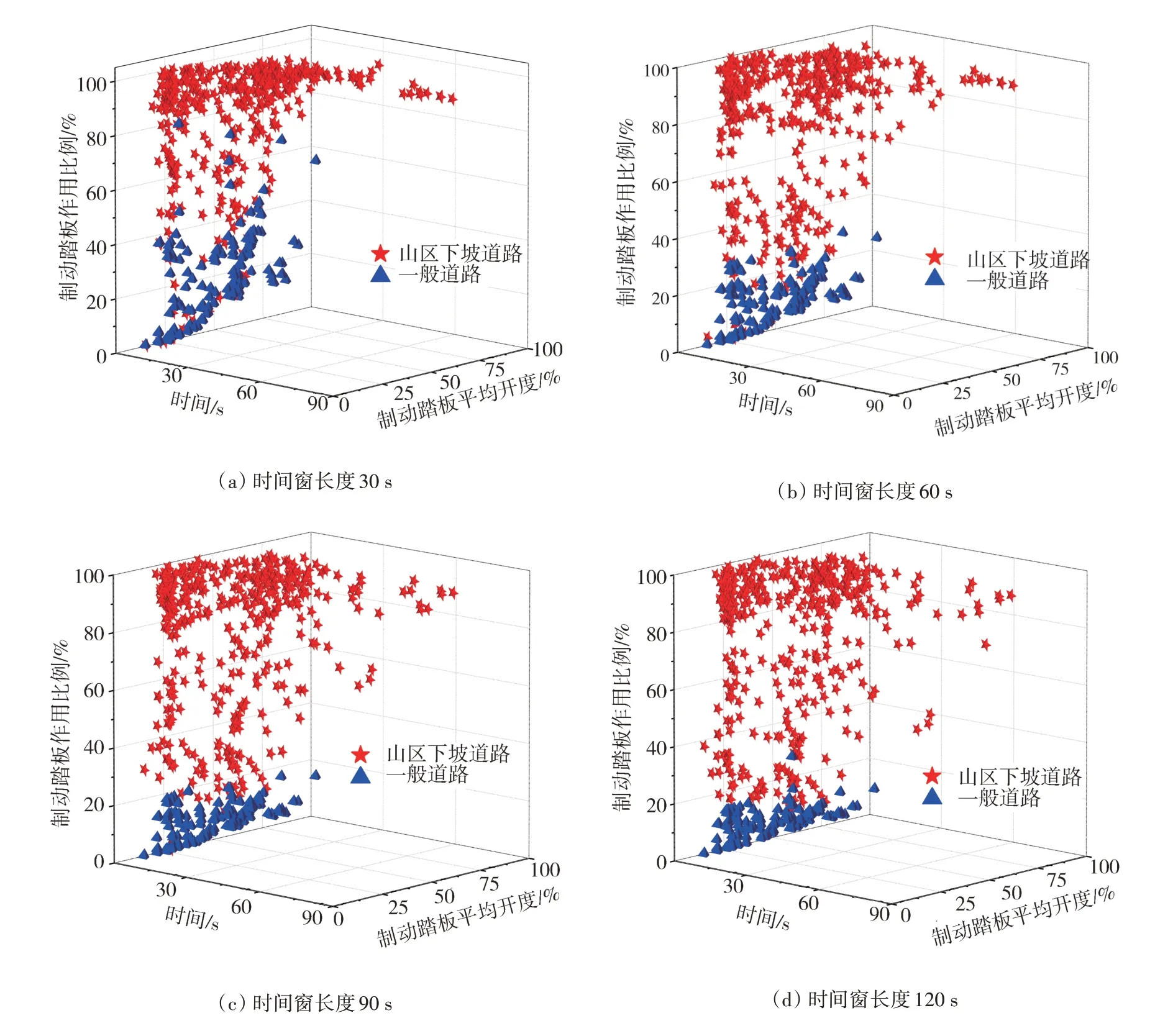
圖2 不同時間窗長度訓練數據

圖2（a）時間窗長度為30 s，兩種工況時間窗內制動踏板作用比例邊界不是很明確，在20%-40%范圍內有交叉；圖2（b）時間窗長度為60 s 時，20%-40%范圍內交叉數據明顯減少；時間窗長度為90和120 s時，長下坡道路和一般道路工況數據相對集中，邊界較為清晰。剔除異常數據，分別訓練長下坡道路和一般道路工況模型。

為驗證兩種行駛工況模型的準確性，提取1 000 s山區公路行駛制動踏板動作數據，見圖3，制動踏板作用時間接近50%，制動踏板作用時平均開度大于40%。制動踏板作用時不同時間窗辨識率為100%，見圖4，行駛工況辨識結果見圖5。

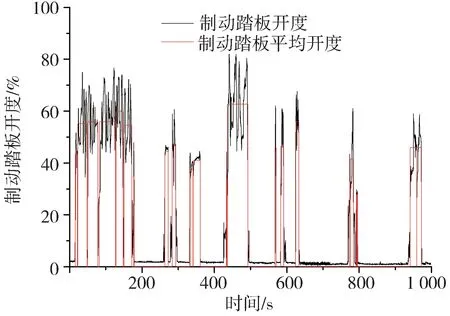
圖3 行駛工況辨識驗證制動踏板數據

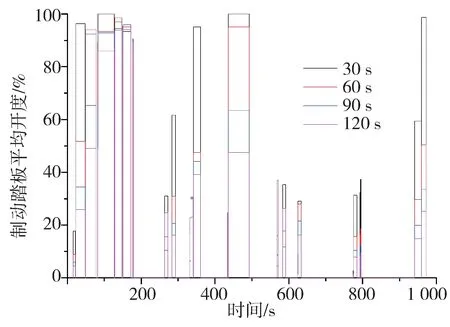
圖4 不同時間窗辨識結果

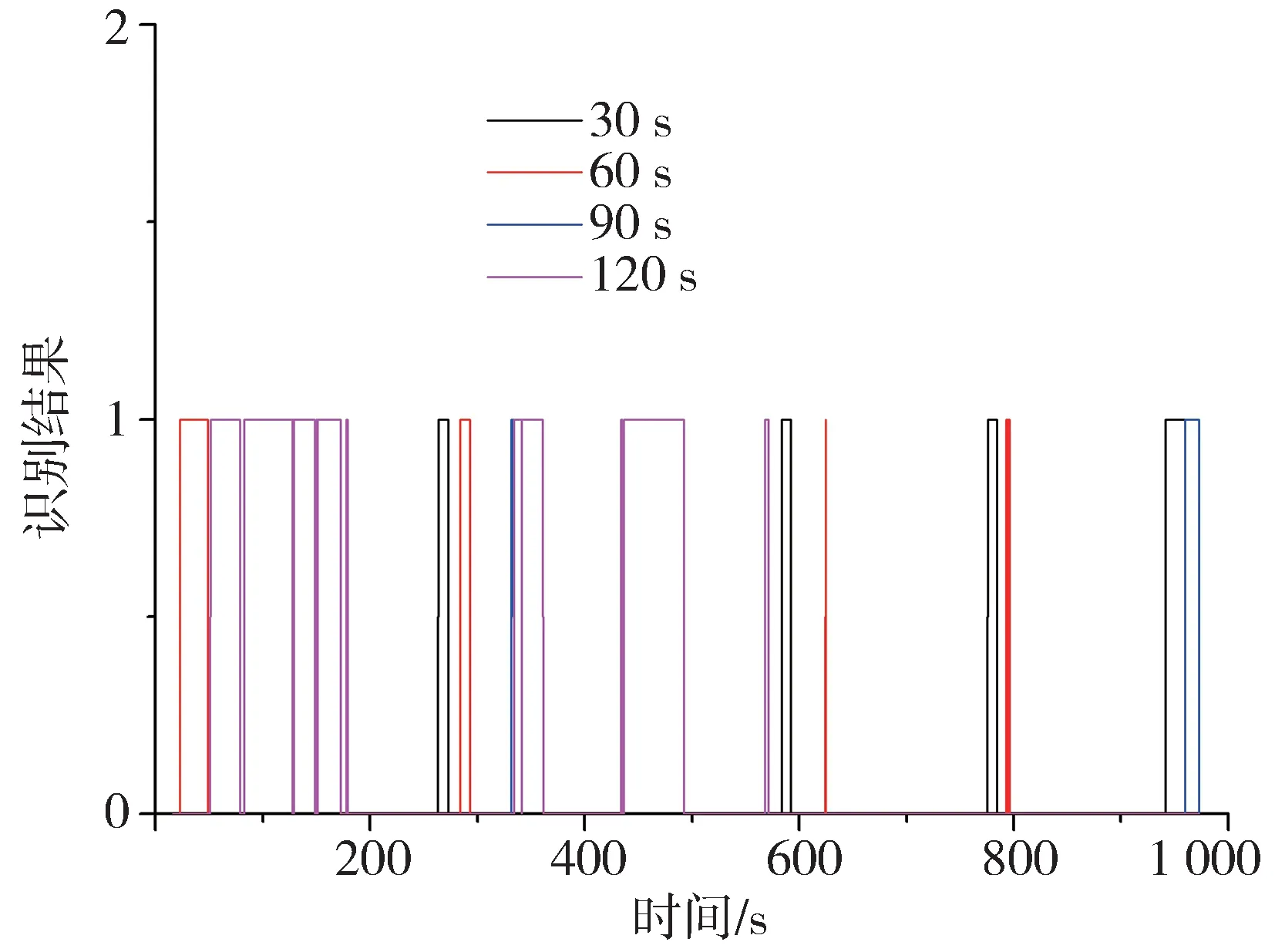
圖5 行駛工況辨識結果

時間窗為30 和60 s 時，模型對制動踏板動作較為敏感，持續作用較短時間即識別為長下坡制動工況，降低了模型識別的準確率。與前兩種時間窗尺度相比，90 s 時間窗對制動踏板動作敏感度降低。時間窗長度為120 s時，模型對制動踏板持續作用時間短的動作敏感度最低，長下坡制動工況識別準確率提高，但是容易忽略了制動踏板頻繁作用對制動系統效能恒定性的影響，因此時間窗長度選擇90 s為宜。

2 排氣制動系統控制策略

排氣制動系統通過增加發動機排氣阻力，倒拖發動機曲軸旋轉而將制動力傳遞給驅動輪，制動過程不依賴行車制動系統，因此長大下坡路段能夠降低行車制動系統熱負荷。但是，目前排氣制動系統開啟由駕駛人手動控制，常常因為駕駛經驗不足或路況不熟悉等原因引發不必要的制動器熱衰退事故，為此本文提出基于道路行駛工況辨識的重型載貨汽車排氣制動系統主動控制方法。

為研究排氣制動系統主動控制方法，文中依據典型長下坡路段道路試驗的方法，用不同時間窗尺度的時間窗內的制動踏板平均開度、制動踏板作用時間和制動踏板作用比例為特征參數，構建了長大下坡道路和一般道路行駛工況，建立隱馬爾可夫工況辨識模型用于在線辨識。當系統感知到制動踏板動作時，在線辨識車輛行駛狀態，判別車輛是否處于頻繁或者持續制動狀態。當系統識別車輛處于長下坡制動工況時，排氣制動系統自動介入工作；當車輛速度降低（轉速降低，輸出制動力受到限制）到安全范圍或者加速踏板介入工作時，自動解除排氣制動系統，控制策略如圖6所示。

圖6 長下坡制動工況持續制動控制策略

3 控制策略驗證

3.1 車輛模型構建

為了驗證本文提出的控制策略，建立了車輛動力學模型和制動系統模型，根據車輛系統動力學理論［22］，當車輛處于制動狀態時，驅動力為0。

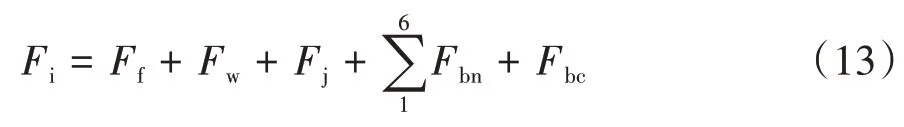
式中：Fbn為制動器制動力；Fbc排氣制動制動力，作用于驅動軸；Fj為加速阻力；Fi為坡度阻力；Ff為滾動阻力，Fw為空氣阻力，滾動阻力和空氣阻力之和由道路試驗獲得。

依據儲氣筒壓力變化建立制動系統模型［23］，制動氣室壓力與儲氣罐壓力的關系為

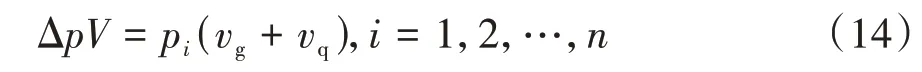
式中：Δp為儲氣罐壓降，kPa；V為儲氣罐體積；vg為制動管路體積；vq為制動氣室容積。

制動氣室通過膜片彈簧推桿作用與車輪的制動力可表示為

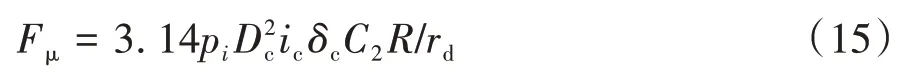
式中：pi為制動氣室的氣壓；Dc為制動氣室的有效直徑；δc為制動凸輪支撐的傳動效率；C2為制動器效能因數；rd為輪胎動負荷半徑；ic為制動凸輪的力傳動比。

鼓式制動器溫度模型［24］可以表示為

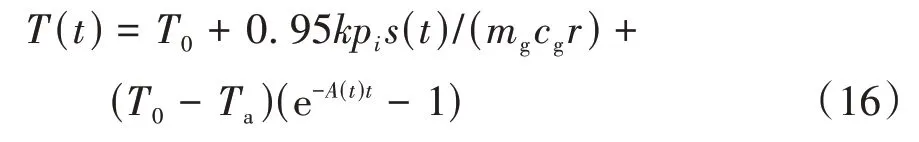
式中：A(t)=(5.224+1.5525v(t)e-0.0027785v(t))A2/(mgcg)；T(t)為制動鼓溫度；T0為制動鼓初始溫度；s(t)為制動距離；Ta為制動鼓外側空氣溫度；k為制動器結構參數；mg為制動鼓質量；cg為制動鼓比熱容；r車輪滾動半徑；A2制動鼓外表面面積。

3.2 控制策略驗證及對比

為驗證文中提出的控制策略，在雅康高速分別進行了發動機制動、排氣制動試驗，并進行仿真對比。試驗車速60 km/h，道路平均坡度2.3%，試驗路段長6 km，結果如圖7和圖8所示。

圖7 發動機制動試驗

圖8 排氣制動試驗

發動機制動試驗過程中行車制動系統持續工作，試驗結束掛車制動器溫度升高值較高，第4 軸和第6 軸溫度分別升高了40.63 和62.54 ℃，牽引車第2軸和第3軸升高了30.39和36.77 ℃。采用30、60、90和120 s時間窗都能夠準確識別制動踏板動作，并分別于150.3、180.2、210.1 和240.2 s 判定為長下坡道路行駛工況。

排氣制動試驗開始階段，駕駛人手動打開排氣制動系統，一直持續到試驗結束，制動踏板動作15次，制動總時長僅占試驗時間的22.35%，制動器溫度大幅降低，第4 軸和第6 軸溫度僅升高了20.56 和24.12 ℃，牽引車第2 軸和第3 軸僅升高了17.16 和26.41 ℃。

為了驗證文中提出主動控制策略的效果，建立了車輛動力學模型、制動系統模型和制動器溫度模型，分別仿真30、60、90 和120 s 時間窗控制效果。仿真結果統計見表2，不同時間窗主動控制策略制動器作用時間均長于排氣制動手動控制，制動器作用次數接近，但是均能避免因駕駛人頻繁制動而忽略排氣制動控制。工況識別過程制動踏板頻繁作用導致制動器溫度上升較快，90和120 s時間窗較為明顯，90 s 時間窗識別階段第6 軸溫度升高了18 ℃，其余軸略低于18 ℃，排氣制動開啟后溫度上升較為緩慢，仿真試驗結束第3 軸和第6 軸溫度分別升高了28.48 和32.38 ℃，其余兩軸升高值略低。以90 s 時間窗進行工況識別主動控制仿真，仿真結果見圖9。

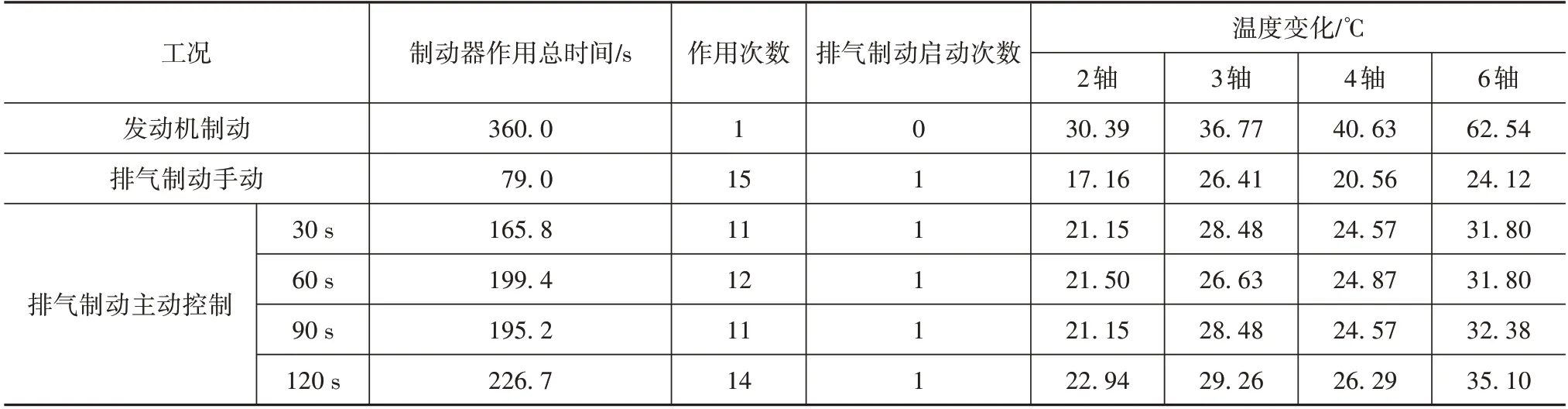
表2 控制策略試驗驗證與仿真對比

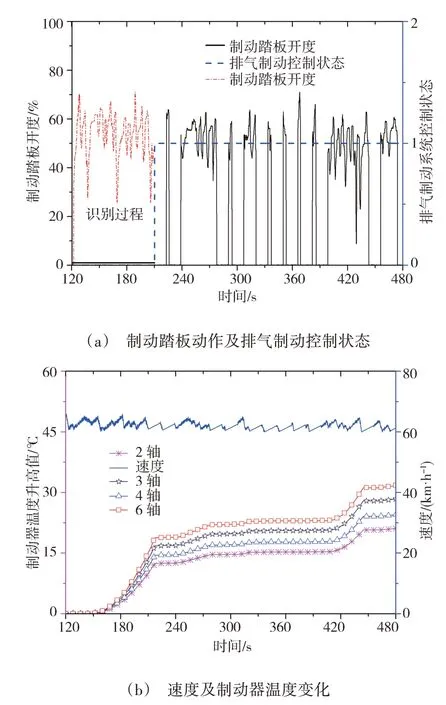
圖9 主動控制系統仿真（90 s時間窗）

4 結論

（1）利用滾動時間窗的方法構建了包含制動踏板平均開度、制動器作用時間和制動踏板作用時間比例參數的重型載貨汽車長下坡道路和一般道路的行駛工況，該工況能夠準確表征車輛行駛的實際狀態。時間窗的長度不宜過長或過短，否則會影響控制效果或者造成工況表達不完整。

（2）高斯函數組成的混合高斯模型能夠解決多維馬爾科夫模型不能直接應用于隨時間連續變化的量的問題，提高了工況辨識的適用性和準確性。

（3）受道路條件的限制，缺乏頻繁開啟制動踏板制動工況的驗證和評價，時間窗長度等參數需要進一步優化。