多元特征融合的渦扇發動機剩余壽命預測

蔣朝云 李 亞 朱貴富 王海瑞

（昆明理工大學信息工程與自動化學院）

設備或系統在運行與非運行過程中，都會在各種因素的作用下發生退化，當退化量積累到某個臨界點，就會發生故障，甚至失效。 發動機作為動力系統的“心臟”，一旦失效，將會給環境、人員安全及經濟等方面造成不可挽回的損失，故其穩定性、可靠性、維修性和安全性一直是行業關注的焦點。

為提高發動機的相關性能、 降低維修成本，提高系統維護的可承受性，發動機剩余使用壽命（Remaining Useful Life，RUL） 已成為當前研究的熱點［1］。在現有的研究中，關于設備或系統在退化建模與壽命預測方面的探索已有眾多研究成果，包括不同的方法和技術。 王璽等采用非線性Wiener過程對發動機進行性能退化建模并實現了RUL的預測［2］。 王國鋒等研究了基于Gamma過程的諧波減速器性能退化過程［3］。主要方法為：首先基于設備性能退化數據構建退化模型，其次根據實時監測數據實現對模型參數的實時更新，進而結合RUL概率密度函數進行RUL的預測。 在此類方法中，大多采用單一傳感器在單一工況下的研究方法，這種方法僅在特定情況下有效。 劉帥君分別從單監測參數與多監測參數兩方面對發動機退化過程進行了描述［4］。近年來，隨著傳感器技術的飛速發展，對目標設備的監測往往采取同時多個傳感器監測的方式，該方式引導了學者采用多傳感器數據進行實驗研究，但也只運用了單一特征提取方式對多傳感器數據進行性能退化描述。 郭慶和李印龍利用專家經驗并結合核主成分分析（Kernel Principal Component Analysis，KPCA）對多傳感器數據建立了航空發動機退化健康指標［5］。 劉幗巾等利用自編碼器對狀態監測數據進行特征提取并構建了健康指標［6］。 洪驥宇等利用降噪自編碼器提取出有利于評估剩余壽命的數據特征［7］。隨著工業程度不斷提高，設備的結構也日益復雜，針對不同的預測對象以及數據類型需要根據其失效機理的認知程度以及數據量的大小來選擇特征提取方式，如果選擇錯誤可能會導致預測結果發生較大誤差甚至失敗。 故依賴單一特征提取方式并不足以準確描述系統的潛在退化機制，單一特征提取方式的局限性導致了預測精度的局限性。

特征提取方法多種多樣，不同方式各有其側重點，側重點不同導致其存在不同的特性［7］。為避免主觀選擇特征提取方式導致結果的偏差，可以采用組合方式對數據進行特征提取，即分別采用不同的特征提取方式對原始數據進行特征提取然后進行特征融合，使各類方式揚長避短，較大限度地發揮各類方式的長處。 此外，眾多研究結果表明，Wiener過程能夠較好地描述系統的退化過程［8］，該模型在設備剩余使用壽命預測領域中得到了廣泛應用。

在此，筆者提出一種多元特征融合的渦扇發動機RUL預測方法： 將多種特征提取方式所得特征向量線性融合構建一個能夠準確表征發動機退化情況的復合健康指標（Composite Health Indicators，CHI）；利用預測壽命與真實壽命均方誤差最小化方法確定各特征向量的融合系數；采用線性Wiener過程對CHI進行退化建模， 實現發動機RUL的實時預測。 最后通過渦扇發動機退化仿真數據集驗證筆者所提方法的有效性。

1 多元特征提取

1.1 數據預處理

考慮到數據在時間上的相關性，采用改進后的指數平滑法（Exponential Smoothing，ES）對渦扇發動機多傳感器數據進行降噪處理［9］，即：

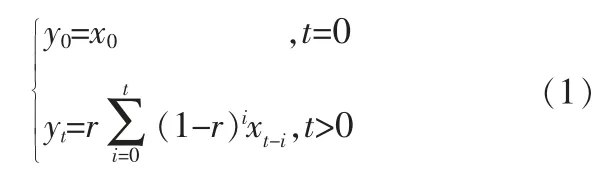
其中，x0、y0分別為初始時刻（t=0）的原始數據值與平滑處理后的值；yt為xt經過平滑處理后的值；衰減因子r=2/（b+1），b=20。該方法在保留原始數據變化趨勢的同時， 達到了平滑與降噪的目的，其根本思想是對歷史數據賦予指數衰減的權重并相加得到當前時刻平滑后的觀測值。

采用歸一化方法將平滑處理后的數據限定在［0，1］之間，即：

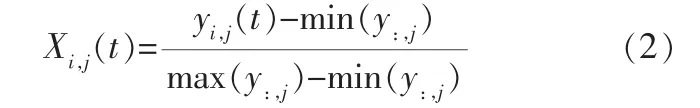
其中，Xi，j（t）為yi，j（t）經過歸一化后的觀測值；max（y：，j）、min（y：，j）分別為N臺訓練發動機中第j個傳感器監測數據的最大值與最小值。 同時，為防止歸一化后數據值過大或過小導致的溢出問題，采用如下方法進行處理：若Xi，j（t）＞1，則Xi，j（t）=1；若Xi，j（t）＜0，則Xi，j（t）=0。 由于經過歸一化后的數據無量綱，所以實驗部分的數據也無量綱。

1.2 特征提取

為融合多種特征提取方式的優點，且考慮到發動機各項性能參數的非線性關系，筆者采取自編碼器（Autoencoder，AE）與KPCA分別對各傳感器數據進行特征提取，為融合CHI做準備。

1.2.1 AE非線性降維

AE［10］在訓練時無需設置標簽，是以輸入作為輸出，能夠對輸入數據進行非線性降維。 AE由編碼器和解碼器兩部分組成，其中編碼器實現輸入數據向隱含層的非線性映射，即：

其中，h為非線性映射關系；g（·）為非線性激活函數；w1、b1為輸入層與隱含層之間的權值和偏置。

解碼器將隱含層特征重構為原始數據，即：

其中，w2、b2為隱含層與輸出層之間的權值和偏置。

網絡以輸入和輸出的誤差為損失函數，即：

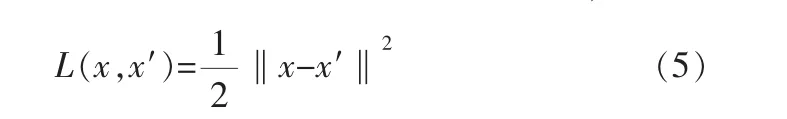
通過L函數的反向傳播不斷調整網絡參數，使其達到最小。

1.2.2 KPCA非線性降維

KPCA是一種非線性主成分分析方法［11］。 令X（t）=（x1，x2，…，xm）表示處理后的傳感器數據，并通過φ（x）映射得到高維空間矩陣Φ（X）=（φ（x1），φ（x2），…，φ（xm））。 其協方差矩陣C為：

對C進行特征值分解得到特征值λ和特征向量W，其中W=（w1，w2，…，wn），且滿足λW-CW=0，進一步有：

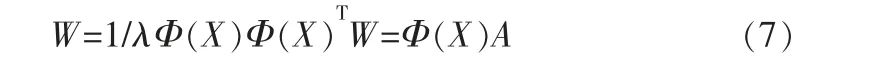
其中，A=（a1，a2，…，am），且ai=1/λiφ（xi）T。

將式（6）代入式（7），并取核函數k（xi，xj）=φ（xi）Tφ（xj）與核矩陣K，可得：

其中，核矩陣K有Kij=k（xi，xj），取高斯核函數：

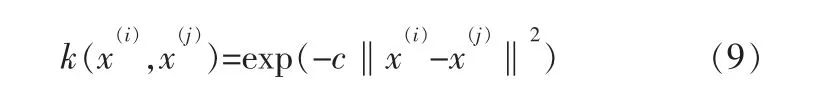
本研究中c取1/20000。

對于任意參數樣本，在特征空間中主元上的投影為：

選取累計貢獻率大于85%的主成分表征發動機退化特性。

2 復合健康指標的構建

2.1 構建CHI

令chii（t）為第i（i=1，2，…，N）個發動機在t時刻的復合健康指標，其計算式為：

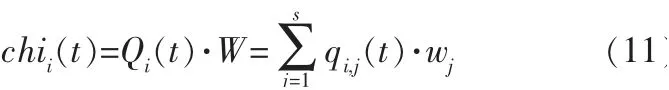
其中，Qi（t）為第i個發動機經過多種特征提取方式整合的特征向量集，Qi（t）=［qi，1（t），qi，2（t），…，qi，s（t）］，qi，j（t）表示第i個發動機第j個特征向量在t時刻的觀測值，s為特征向量個數；W=［w1，w2，…，ws］T為融合系數向量；wj為第j個特征向量的融合系數，表征了該特征向量在融合過程中的權值。

2.2 確定失效閾值

鑒于發動機在實際應用中由于退化過程的不確定性，不同發動機在失效時所對應的退化量有一定偏差。 因此，同類型發動機在相同失效模式下，可以通過待定失效閾值與每個發動機真實失效時刻所對應退化量的方差最小化方法來確定其失效閾值［12］，即有：

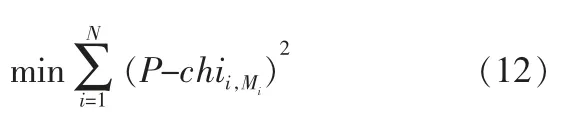
其中，P為發動機待定失效閾值；chii，Mi為第i個發動機在失效時刻tMi時的融合退化量， 由此可得發動機的平均失效閾值為：

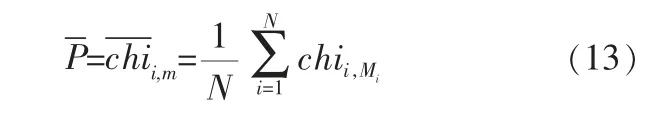
由式（13）得出的平均失效閾值即為式（12）中P的最優解。

2.3 基于線性Wiener過程的退化建模

根據數據特點，采用線性Wiener［13］過程對CHI進行退化建模分析，其過程如下：

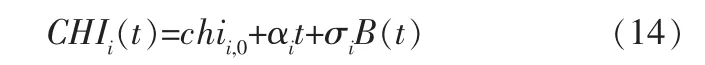
其中，chii，0為第i個發動機的初始退化量；αi表示第i個發動機的漂移系數，描述該發動機的退化率；σi為第i個發動機的擴散系數， 描述發動機在退化過程中的隨機性；B（t）表示標準布朗運動；CHIi（t）為第i個發動機在t時刻的復合退化量。

2.4 求解融合系數

2.4.1 參數估計

其中，Mi為第i臺發動機測量的運行周期數目。

2.4.2 發動機壽命預測

根據線性Wiener隨機退化過程與首達時間（First Hitting Time，FHT）的性質［14］，若發動機性能退化量首次達到或者超過其失效閾值P時， 即判定發動機失效，其壽命Ti可定義為：

2.4.3 確定融合系數

確定融合系數后，便可通過式（11）得到各渦扇發動機的復合健康指標。

3 發動機剩余使用壽命評估

3.1 參數估計

3.1.1 離線參數估計

3.1.2 在線參數估計

對于具體運行的發動機， 需要對漂移系數αi進行實時更新，使模型與發動機實際運行情況更加吻合。根據式（11），某發動機從t=0時刻到t=tk時刻融合健康指標的觀測數據為chi1：k={chi（tr），0=t1≤tr≤tk}。

3.2 在線壽命預測

由式（18）可知第i個發動機在tk時刻的剩余壽命為：

綜上所述，筆者所提的渦扇發動機剩余壽命預測方法流程如圖1所示。

圖1 渦扇發動機RUL預測流程

具體步驟如下：

a.多元特征融合。 首先對發動機多傳感器數據進行降噪、歸一化處理，然后采用不同特征提取方式分別對處理后的數據進行特征提取，再根據多元特征融合公式，以預測剩余壽命與真實剩余壽命均方誤差最小為目標函數得到融合系數。

b.參數估計。 通過數據集離線估計漂移系數α與擴散系數σ，并確定出參數α的初始值，然后結合Bayesian公式實現模型參數αi的在線更新。

c.RUL預測。 結合模型，通過式（27）、（28）獲取發動機的RUL。

d. 方法論證。 將采用單一特征提取方式的RUL預測方法與筆者所提方法進行對比驗證。

4 實驗驗證

4.1 數據集

實驗采用美國宇航局提供的商用模塊化航空推進系統仿真（CommercialModularAero-propulsion System Simulation，C-MAPSS）數 據 集［16］，該 數 據 集為航空渦扇發動機RUL預測領域被廣泛使用的基準數據。 筆者采用該數據集中的FD001數據集進行對比實驗驗證。FD001數據集包含100個同類型發動機的訓練集、測試集和測試集當前所對應的RUL。 其中，訓練集和測試集各包含100個發動機的全壽命歷史監測數據與部分壽命測試數據，每組數據共26列（第1列為發動機號，第2列為運行周期數，第3～5列為運行條件，后21列為機身21處傳感器監測數據）。

4.2 構建健康指標

根據前文所述方法，對渦扇發動機多傳感器數據進行降噪、歸一化處理，然后分別進行自編碼器降維與核主成分分析，得到能表征發動機退化性能的特征向量。

通過AE將多傳感器數據降至一維數據，稱為健康指標1（HI1）；通過KPCA對多傳感器數據進行主元分析，其中部分主成分的相關信息見表1。從表1中可以看出， 第1個主成分的貢獻率高達87.64%（大于85%），其在一定程度上能夠較好地表征發動機性能退化趨勢， 將其稱為健康指標2（HI2）。

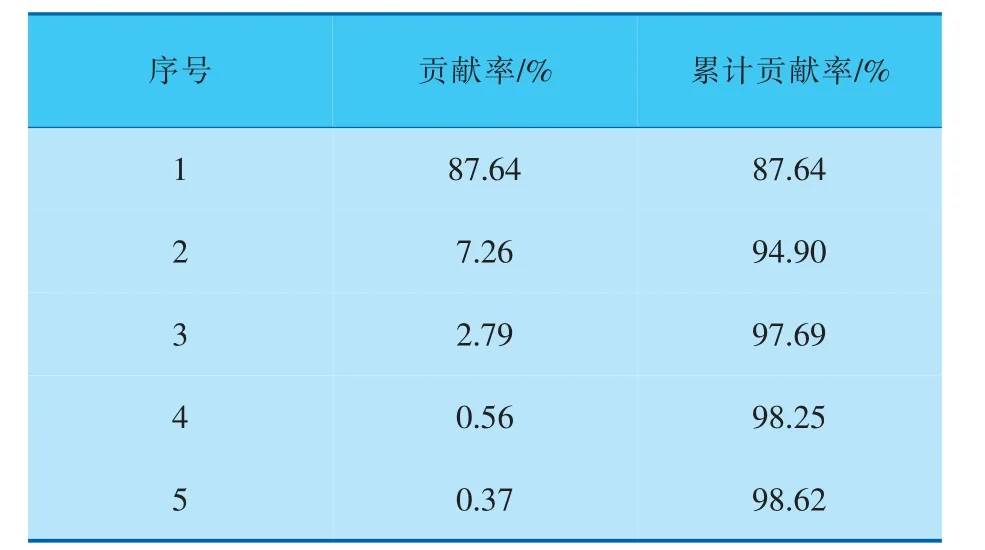
表1 部分主成分的貢獻率分析表

通過筆者所提構建CHI方法， 得到HI1與HI2的融合系數為W=［1.9513 -0.9513］。 由此可得到CHI的觀測數據如圖2所示（發動機運行時間的單位是運行周期數），CHI的閾值P=4.7245， 得到部分發動機的健康參數如圖3所示。

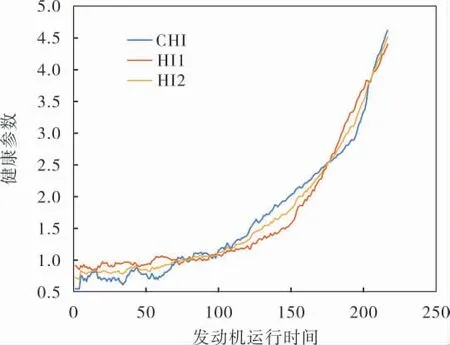
圖2 健康指標觀測數據

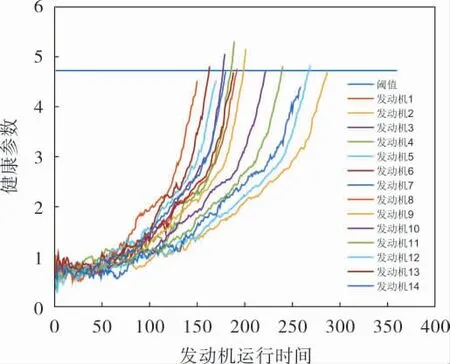
圖3 部分發動機的健康參數

4.3 RUL預測精度對比分析

為體現多元特征融合方法在RUL預測領域的有效性，需對CHI以及HI1、HI2的監測數據分別采用線性Wiener過程進行退化建模分析， 不同方法的模型參數見表2。

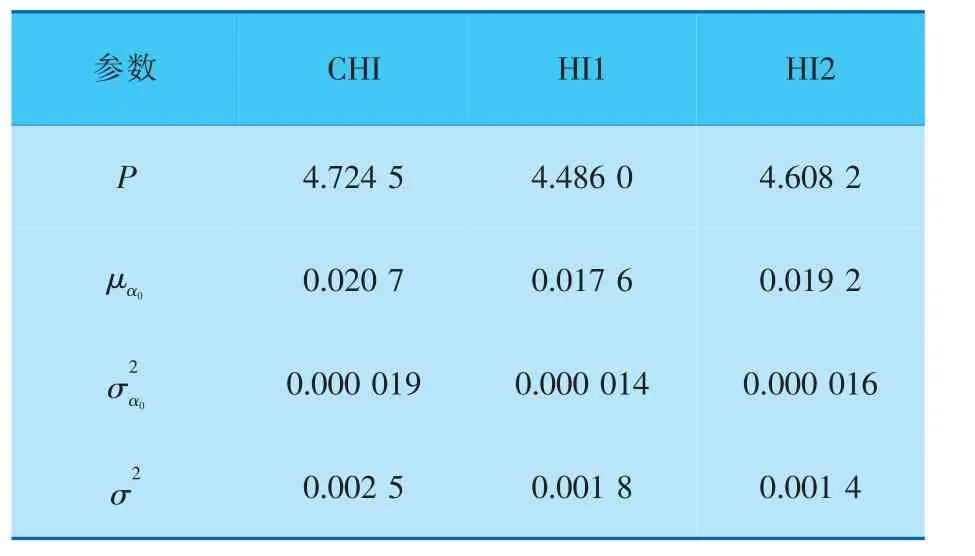
表2 不同方法的模型參數

考慮到根據歷史退化數據估計所得的參數，會隨著實時監測數據的增加而更加貼合發動機退化過程中的真實參數，故實驗選擇發動機最后12個壽命周期進行壽命預測， 得到3種健康指標下的RUL預測結果如圖4所示 （剩余壽命預測時刻、發動機剩余壽命的單位是運行周期數）。

圖4 3種健康指標的RUL預測結果

根據圖4的實驗結果， 可以計算剩余預測壽命的均方根誤差（Root Mean Square Error，RMSE）來量化其預測精度。 RMSE在tk時刻的值可定義為：

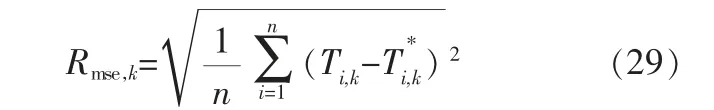
由此可得3種健康指標下發動機在相同運行條件下的Rmse，k值如圖5所示。 從圖5可以看出，隨著發動機運行周期數目的增加，CHI、HI1與HI2下的Rmse，k值都在逐漸變小，且CHI的Rmse，k值最小，相較于HI1與HI2而言整體分別下降了24.93%與8.76%。 實驗結果驗證了基于多元特征融合的渦扇發動機剩余壽命預測方法能夠有效融合多種特征提取方式的優勢， 并提高了RUL預測的準確性。

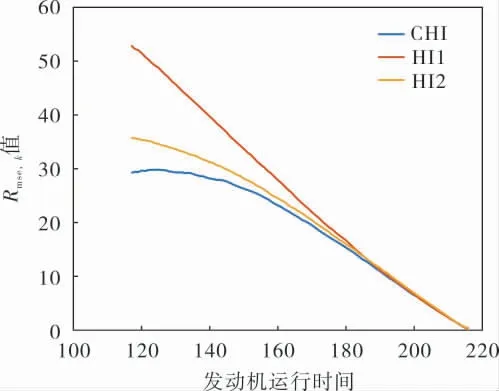
圖5 不同監測點3種健康指標的Rmse，k值

5 結論

5.1 筆者所提方法采用了多種特征提取方式對發動機多傳感器數據進行了深層挖掘，提高了對數據的利用率，增強了特征提取率。

5.2 CHI由多種特征提取方式所得特征融合而成，該健康指標構建方法可以克服基于單一特征提取方式的RUL預測方法在應用中因主觀選擇特征提取方式錯誤而面臨失敗的難題。

5.3 通過對比實驗驗證表明，采用多元特征融合的方法相較于特征融合前均方根誤差整體分別下降了24.93%與8.76%。