初中數學課堂導入方式的探究
江蘇省南京師大附中樹人學校 王 磊
如果說教育是一門藝術,那么課堂導入就是一種創造[1].課堂伊始,利用新穎方法導入能有效喚醒學生的智力情緒,讓學生產生濃厚的學習興趣,使得課堂漸入佳境.因此,導課方式不僅體現了教師的教學基本功,還能活躍課堂氣氛,推進課程進展.
一本引人入勝的好書往往有著精彩的序言,一篇好的文章往往有個好的開頭.同樣,數學課堂的導入,也需要有新穎、引人入勝的方法,以激起學生的學習熱情,讓學生以最好的狀態投入到新知的學習中.因此,精彩的課堂導入既能體現教育的藝術,又能體現數學獨有的創造力.
1 開門見山,直擊目標
隨著新課改的推進,課堂中出現了很多新穎的教學手段.教師要有一雙火眼金睛進行甄別,以確定什么時候該采取哪種教學方式更為妥當.實踐告訴我們,對于有些知識,與其繞一個大圈子去吸引學生的注意力,還不如開門見山地直接呈現來得效果好.
開門見山地直接導入需建立在學生對教學目標有所認識的基礎上,教師將本節課的教學內容直接呈現給學生,讓學生將注意力都集中到知識的學習與探索中,從而提高學生的專注力與自主力[2].
案例1“有理數減法”的教學
“有理數的減法”是七年級的教學內容,學生之前對有理數已經有了比較完整的認識,并掌握了其加法運算的法則.減法的學習對于初中生來說,難度并不大,本節課教學重點是將減法轉化為學生所熟悉的加法即可.因此,也可以簡單地理解為有理數的減法是加法的延伸.
為此,筆者首先帶領學生回顧了有理數加法的運算,要求學生完成以下幾個計算:(-9)+(-4);(+4)+(-2);(-8)+2;(-5)+65;(+5)+(+5).
學生順利解題后,教師直接揭示有理數減法的法則:減某一個數,等于加這個數的相反數,即a-b=a+(-b).
大部分學生對這個定義充滿了探究興趣,幾個活躍的學生表示這個運算法則有點意思,迫不及待地想要嘗試.筆者精選了幾道計算題,供學生試試身手.
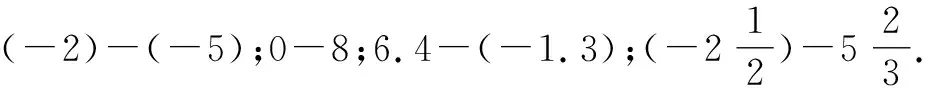
此時,教師高度贊揚學生一點就會的聰慧,同時鼓勵學生思考:有理數減法與加法之間具有怎樣的關系?
學生在自主思考中逐漸完成本節課的教學目標,并在不知不覺中就突破了教學重點與難點.開門見山的課堂導入方式不僅沒有讓學生產生厭煩感或枯燥感,反而有效地激起了學生自主探究的欲望,為培養學生的學力奠定了堅實的基礎.由此可見,課堂導入并非花樣越多越好,而應根據實際教學內容,進行合理選擇,有時最簡單的反而是最合適的.
2 數學故事,引人入勝
我們接觸到的數學知識均是經過歷史的洗禮,逐漸抽象而來.每個知識都經歷了一段又一段的歷史演變與發展的過程,尤其是一些令人欽佩、值得頌揚的數學小故事能刷新學生的認知,為培養學生形成良好的思維品質與人生觀奠定基礎[3].因此,在教學中,可精選一些催人奮進的故事與學生分享,以調動學生學習的積極性,并在數學教育中滲透德育教育,以提升學生的數學核心素養.
案例2“平面直角坐標系”的教學
“平面直角坐標系”是一個對數學學習具有重要影響的知識點,但這又是一個相對枯燥與抽象的知識點.因此,正式授課之前,筆者以笛卡兒的故事吸引學生的注意力,讓學生先對此知識產生良好的情感傾向,以削弱學習的枯燥與乏味.
故事情境:年輕的笛卡兒是一位軍人,一天他在睡夢中看到許多數學家,有阿基米德、畢達哥拉斯、歐幾里得、希伯索斯等.他們正在一起討論“如何將一個平面內的點和數聯系到一起”,因為討論得太投入,竟然沒有人注意到笛卡兒這個不速之客.此時,笛卡兒撿起地上的一把鑰匙,輕輕打開了屋內的一扇門,正當他走進去時,夢竟然醒了.(學生都被笛卡兒的夢境所吸引,一個個興致盎然地期待教師繼續說接下來發生了什么.)醒來的笛卡兒迷迷糊糊地睜開眼,看到月光投射到墻角的一張蜘蛛網上,突然靈光一閃,一個念頭劃過腦際:若蜘蛛是一個點,它可沿著蜘蛛網上下左右來回移動,那么蜘蛛網豈不是縱橫交錯的線?蜘蛛爬到哪個位置,就可以用兩個數字來表示了.由此,馳騁于數學界的平面直角坐標系就產生了.
每個學生都被笛卡兒神奇的夢境與偉大的發明所震撼,趣味性的歷史故事快速吸引了學生的注意力.在接下來的學習中,因學生對平面直角坐標系有著一定的情感傾向,導致學習進程尤為順利,每個學生對該知識的學習都倍感親切,從而積極主動地參與探索與思考.因此,利用歷史小故事的課堂導入,不僅給課堂增添了趣味性,還有效地拉近了學生與知識的距離.
3 活動開展,引發探究
心理學與教育學共同研究表明,人類對新知的認識與建構,主要是在實踐過程中思維呈螺旋式上升而達成.因此,這就要求教師在教學中,設置一些落在學生最近發展區的操作活動,讓學生在充足的時間與空間內通過實踐操作,完成對知識的認識與理解.如此,則能讓學生更加具體、深刻地理解教學內容,掌握所學知識.
案例3“立體圖形與平面圖形”的教學
立體圖形與平面圖形的內容比較抽象,若教師以傳統的授課模式講解,學生很難從根本上理解立體圖形展開后,如何獲得相應的平面圖形.因此,筆者以活動導入的方式,讓學生在直觀操作中充分認識二者之間的聯系.
活動準備:立方體紙盒、剪刀、水彩筆、磁吸、立體圖模型、多媒體等.
活動設計:運用小組合作學習方式讓學生在自主操作、觀察中探究、感知數學活動的樂趣,體驗成就感.
活動過程:
(1)要求學生將正方體的相對面分別涂上相同的顏色,每個對立面之間的顏色不一樣.
(2)獨立將自己手中的正方體剪開,按照自己的想法去剪,剪開后的圖為一整張圖形即可.
(3)以小組為單位,觀察組內成員的展開圖,同時思考兩個問題:①有多少種不同的展開方式?有沒有一定的規律性?②觀察展開圖中相對的面是否存在某種規律?
師:哪個小組愿意展示一下本組的正方體展開圖?
組1:如圖1,我們組展開后得到六種圖形.

圖1
師:大家看看這六組圖形與你們組的一樣嗎?
組2:有一樣的,也有不一樣的,我們組還出現了以下三種圖形,如圖2.

圖2
組3:除了以上九種之外,還有兩種圖形他們兩組都沒有展示.
師:哦?哪兩種?
(組3展示圖3)

圖3
師:還有補充的嗎?
(眾生搖頭)
師:我們來觀察這些圖,看看是否存在什么規律?
生1:我們可以把圖形重新排列.四格在一條線上的排在一起,如圖4;其他的排一起,如圖5 .

圖4
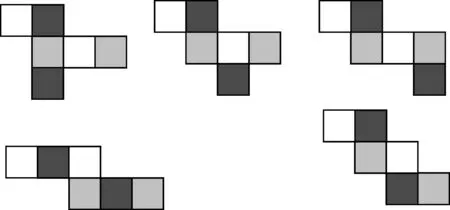
圖5
觀察可得以下規律:①四方一線兩相望;②一馬單腿兩階梯.
師:很好!相對的面之間存在什么規律?
生2:同一行或列中間隔一個其他的顏色,若不在同一行或列的,就沒有公共的頂點.
…………
此活動的導入既尊重了學生之間的認知差異性,又有效地發展了學生多元化的數學思維.每個學生按照自己的習慣剪開正方體紙盒,并通過小組合作學習的機會觀察同伴的展開成果,發現一個普通的正方體展開后竟然有多種不同的圖形;再觀察圖形相對面的規律,以對展開后的圖形產生深刻認識;同時,學生在合作中也積累了良好的活動經驗,有效地提升了自身的數學理解能力與實際操作能力.
總之,為了適應時代需求,教師需結合授課內容與學生實際情況,靈活選擇合適、合理的課堂導入方式,以激發學生的探究興趣,為課堂的有效性奠定基礎.

