2022年高考“概率與統計”試題分析及復習建議

張 琥(正高級教師 特級教師)

(北京外國語大學附屬蘇州灣外國語學校)

1 考試內容分析

概率與統計是中學數學課程中的主要內容之一,?普通高中數學課程標準(2017年版2020年修訂)?對這部分內容的設置較?普通高中數學課程標準(實驗)?有所增加.2022年高考全國卷中概率與統計試題重在對基礎知識的考查,突出對數學思想方法、統計與概率的基本原理的理解和應用.2022年高考全國卷中考查概率與統計的主要內容如表1所示.

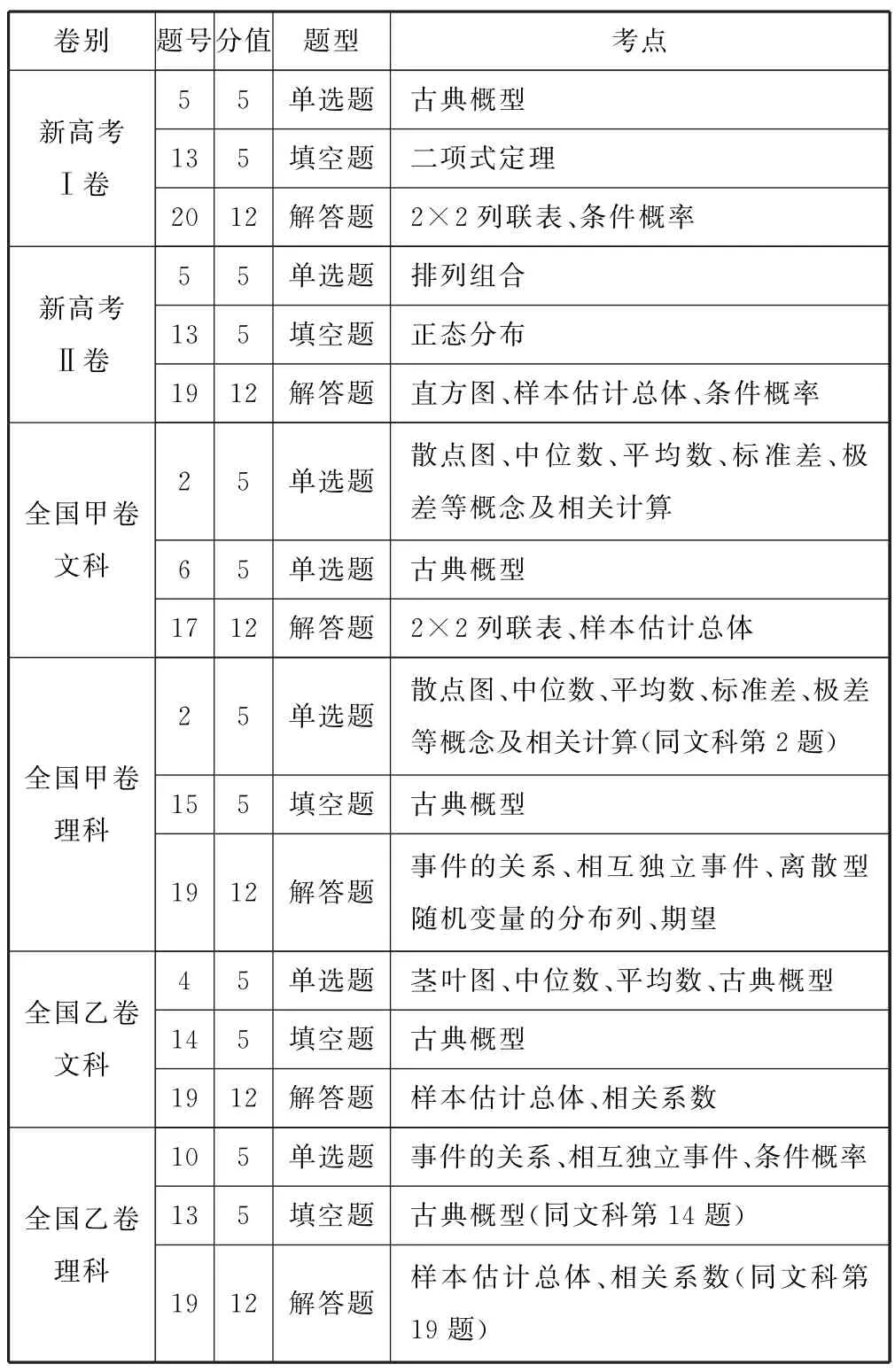
表1

從表1可以看出,在6份全國卷中,對統計與概率知識的考查,題型均是2 道小題和1 道大題,共3道題,所占分值均是22分.新高考Ⅱ卷考查了條件概率,其他5份試卷均考查的是古典概型;新高考Ⅱ卷、全國(甲、乙)卷文科、全國乙卷理科均考查了用樣本的數字特征估計總體的數字特征.

2 試題特點分析

6份全國卷中的概率與統計題特點鮮明,涉及知識點有排列組合、二項式定理、古典概型、樣本平均數、樣本方差、線性回歸、正態分布、獨立性檢驗等.在以統計知識為背景下考查概率問題,還常常在與函數知識的交會處命題,命題背景多與生產生活聯系,體現一定的綜合性和應用性.

2.1 知識考查重理解

例1 (2022年全國甲卷理15)從正方體的8個頂點中任選4 個,則這4 個點在同一個平面的概率為________.

2.2 方法考查重積累

例2(2022年新高考Ⅱ卷19)在某地區進行流行病學調查,隨機調查了100 位某種疾病患者的年齡,得到如下的樣本數據的頻率分布直方圖(如圖1).

圖1

(1)估計該地區這種疾病患者的平均年齡(同一組中的數據用該組區間的中點值為代表);

(2)估計該地區一位這種疾病患者的年齡位于區間[20,70)的概率;

(3)已知該地區這種疾病的患病率為0.1%,該地區年齡位于區間[40,50)的人口占該地區總人口的16%.從該地區中任選一人,若此人的年齡位于區間[40,50),求此人患這種疾病的概率(以樣本數據中患者的年齡位于各區間的頻率作為患者的年齡位于該區間的概率,精確到0.0001).

(2)由頻率穩定于概率的原理,用樣本的頻率作為概率的估計值,設A＝{一人患這種疾病的年齡在區間[20,70)},根據對立事件的概率公式P(A)＝1－P(ˉA),可求出年齡位于區間[20,70)的概率為0.89.

(3)根據條件概率公式即可求出此人患這種疾病的概率約為0.0014.

2.3 技能考查重熟練

例3(2022年北京卷18)在校運動會上,只有甲、乙、丙三名同學參加鉛球比賽,比賽成績達到9.50m以上(含9.50m)的同學將獲得優秀獎.為預測獲得優秀獎的人數及冠軍得主,收集了甲、乙、丙以往的比賽成績,并整理得到如下數據(單位:m).

甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;

乙:9.78,9.56,9.51,9.36,9.32,9.23;

丙:9.85,9.65,9.20,9.16.

假設用頻率估計概率,且甲、乙、丙的比賽成績相互獨立.

(1)估計甲在校運動會鉛球比賽中獲得優秀獎的概率;

(2)設X是甲、乙、丙在校運動會鉛球比賽中獲得優秀獎的總人數,估計X的數學期望E(X);

(3)在校運動會鉛球比賽中,甲、乙、丙誰獲得冠軍的概率估計值最大? (結論不要求證明)

(2)求解出X的分布列,從而可計算出X的數學期望為

(3)計算出甲、乙、丙得最高成績的概率,再根據其最高成績可判斷出丙獲得冠軍的概率估計值最大.

3 解題分析

例4(2022年新高考Ⅰ卷5)從2至8的7個整數中隨機取2個不同的數,則這2個數互質的概率為( ).

例5(2022年全國甲卷文6)從分別寫有1,2,3,4,5,6的6張卡片中無放回地隨機抽取2張,則抽到的2 張卡片上的數字之積是4 的倍數的概率為( ).

例6(2022年新高考Ⅱ卷5)有甲、乙、丙、丁、戊5 名同學站成一排參加文藝匯演,若甲不站在兩端,丙和丁相鄰,則不同排列方式共有( ).

A.12種 B.24種 C.36種 D.48種

例7(2022年全國乙卷文14、理13)從甲、乙等5名同學中隨機選3名參加社區服務工作,則甲、乙都入選的概率為________.

例9(2022年北京卷8)若(2x－1)4＝a4x4＋a3x3＋a2x2＋a1x＋a0,則a0＋a2＋a4＝( ).

A.40 B.41 C.－40 D.－41

例10(2022年全國甲卷文、理2)某社區通過公益講座以普及社區居民的垃圾分類知識.為了解講座效果,隨機抽取10位社區居民,讓他們在講座前和講座后各回答一份垃圾分類知識問卷,這10 位社區居民在講座前和講座后問卷答題的正確率如圖2 所示,則( ).

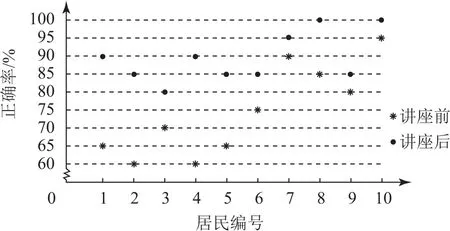
圖2

A.講座前問卷答題的正確率的中位數小于70%

B.講座后問卷答題的正確率的平均數大于85%

C.講座前問卷答題的正確率的標準差小于講座后正確率的標準差

D.講座后問卷答題的正確率的極差大于講座前正確率的極差

例11(2022年全國乙卷文4)分別統計了甲、乙兩位同學16 周的各周課外體育運動時長(單位:h),得到如圖3所示的莖葉圖,則下列結論中錯誤的是( ).

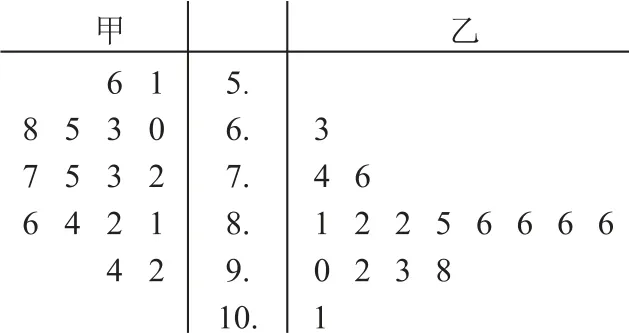
圖3

A.甲同學周課外體育運動時長的樣本中位數為7.4

B.乙同學周課外體育運動時長的樣本平均數大于8

C.甲同學周課外體育運動時長大于8的概率的估計值大于0.4

D.乙同學周課外體育運動時長大于8的概率的估計值大于0.6

綜上,選C.

例12(2022年新高考Ⅱ卷13)已知隨機變量X服從正態分布N(2,σ2),且P(2＜X≤2.5)＝0.36,則P(X＞2.5)＝________.

例13(2022年新高考Ⅰ卷20)一醫療團隊為研究某地的一種地方性疾病與當地居民的衛生習慣(衛生習慣分為良好和不夠良好兩類)的關系,在已患該疾病的病例中隨機調查了100例(稱為病例組),同時在未患該疾病的人群中隨機調查了100人(稱為對照組),得到如表2所示的數據.

表2

(1)能否有99%的把握認為患該疾病群體與未患該疾病群體的衛生習慣有差異?

(2)從該地的人群中任選一人,A表示事件“選到的人衛生習慣不夠良好”,B表示事件“選到的人患有該疾病的比值是衛生習慣不夠良好對患該疾病風險程度的一項度量指標,記該指標為R.

(ⅱ)利用該調查數據,給出P(A|B),P(A|ˉB)的估計值,并利用(ⅰ)的結果給出R的估計值.

表3

又P(K2≥6.635)＝0.01,24＞6.635,所以有99%的把握認為患該疾病群體與未患該疾病群體的衛生習慣有差異.

(2)(ⅰ)因為

例14(2022 年全國乙卷理10)某棋手與甲、乙、丙三位棋手各比賽一盤,各盤比賽結果相互獨立.已知該棋手與甲、乙、丙比賽獲勝的概率分別為p1,p2,p3,且p3＞p2＞p1＞0.記該棋手連勝兩盤的概率為p,則( ).

A.p與該棋手和甲、乙、丙的比賽次序無關

B.該棋手在第二盤與甲比賽,p最大

C.該棋手在第二盤與乙比賽,p最大

D.該棋手在第二盤與丙比賽,p最大

記該棋手在第二盤與乙比賽,且連勝兩盤的概率為p乙,則

記該棋手在第二盤與丙比賽,且連勝兩盤的概率為p丙,則

即p甲＜p乙,p乙＜p丙,則該棋手在第二盤與丙比賽,p最大,所以D 正確,B 和C 錯誤.p與該棋手與甲、乙、丙的比賽次序有關,所以A 錯誤.

綜上,選D.

例15(2022年全國乙卷文、理19)某地經過多年的環境治理,已將荒山改造成了綠水青山.為估計一林區某種樹木的總材積量,隨機選取了10棵這種樹木,測量每棵樹的根部橫截面積(單位:m2)和材積量(單位:m3),得到如表4所示的數據.

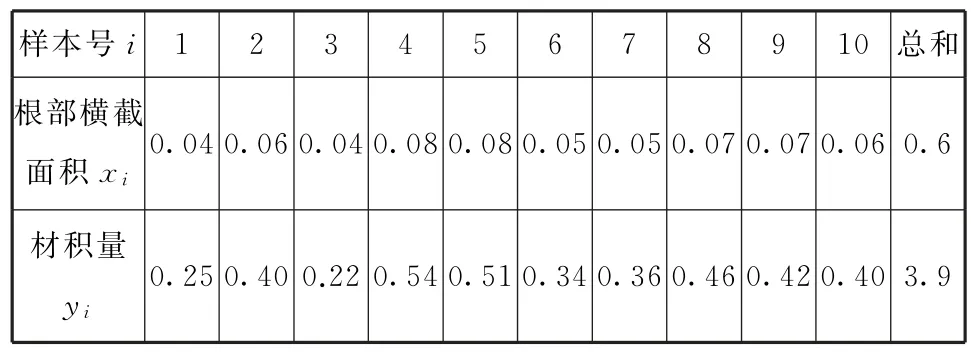
表4

(1)估計該林區這種樹木平均一棵的根部橫截面積與平均一棵的材積量;

(2)求該林區這種樹木的根部橫截面積與材積量的樣本相關系數(精確到0.01);

(3)現測量了該林區所有這種樹木的根部橫截面積,并得到所有這種樹木的根部橫截面積總和為186m2.已知樹木的材積量與其根部橫截面積近似成正比,利用以上數據給出該林區這種樹木的總材積量的估計值.

(3)設該林區這種樹木的總材積量的估計值為Ym3,又已知樹木的材積量與其根部橫截面積近似成正比,可得解得Y＝1209 m3,則該林區這種樹木總材積量估計為1209m3.

例16(2022年全國甲卷文17)甲、乙兩城之間長途客車均由A和B兩家公司運營,為了解這兩家公司長途客車的運行情況,隨機調查了甲、乙兩城之間的500個班次,得到列聯表如表5所示.

表5

(1)根據上表,分別估計這兩家公司甲、乙兩城之間的長途客車準點的概率;

(2)能否有90%的把握認為甲、乙兩城之間的長途客車是否準點與客車所屬公司有關?

表6

(2)列聯表如表7所示.

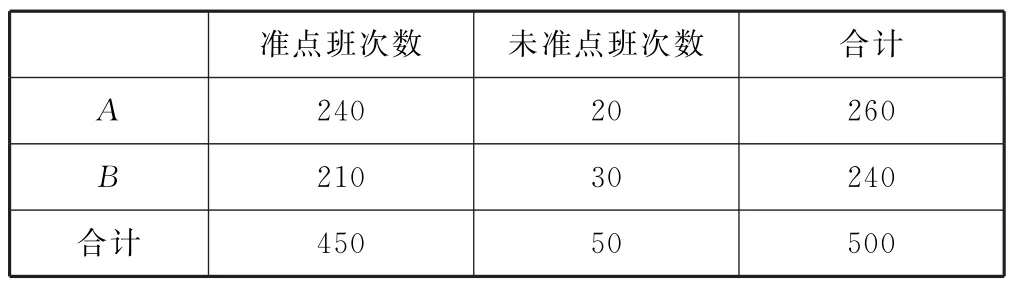
表7

根據臨界值表可知,有90%的把握認為甲、乙兩城之間的長途客車是否準點與客車所屬公司有關.

例17(2022年全國甲卷理19)甲、乙兩個學校進行體育比賽,比賽共設三個項目,每個項目勝方得10分,負方得0分,沒有平局.三個項目比賽結束后,總得分高的學校獲得冠軍.已知甲學校在三個項目中獲勝的概率分別為0.5,0.4,0.8,各項目的比賽結果相互獨立.

(1)求甲學校獲得冠軍的概率;

(2)用X表示乙學校的總得分,求X的分布列與期望.

(2)依題可知,X的可能取值為0,10,20,30,所以

即X的分布列如表8所示.

表8

4 命題趨勢

通過對近年全國高考卷,特別是近三年新高考卷的分析與研究,我們預計2023年高考對概率與統計的考查將繼續秉持新高考卷的命題風格,強調對基本概念和基本公式的理解、應用,突出對運算求解能力和數據處理能力的考查.

4.1 考查排列組合的內容

排列組合部分仍會突出對兩個計數原理、排列組合等基本知識的考查,多以選擇題、填空題為主,如2021年全國乙卷理科第6題.

4.2 考查二項式定理的內容

高考中對二項式定理的考查主要是基礎知識和基本運算,以小題形式出現,沒有難題.因為二項式定理的應用比較廣泛,在復習過程中,我們還要關注與二項展開式中的系數有關的最值和二項式定理的逆用的問題.

4.3 考查概率的內容

概率部分試題形式基本穩定,考點比較集中,以傳統優秀文化、生產生活實際為背景的概率問題屢見不鮮.古典概型、隨機事件概率的計算和正態分布等考點均會出現在客觀題中,2021年新高考Ⅰ,Ⅱ卷中是以多選題形式出現,考查的重點還是古典概型.如2019年全國Ⅰ卷理科第7題就是從我國古代典籍?周易?中的“卦”演變而來,需要考生認真審題與閱讀,抓住概率類型,運用古典概型公式快速求解.條件概率、隨機變量的分布列與數字特征、二項分布、超幾何分布、正態分布仍然是命題的重點,且多以解答題形式出現.如2022年新高考Ⅰ卷第20 題,新高考Ⅱ卷第19題,全國甲卷理科第19題等對條件概率、隨機變量分布列與數字特征、二項分布都進行了深入的考查.

4.4 考查統計的內容

統計思想與原理的廣泛應用是數學與生產生活實際聯系的重要紐帶.在近幾年的高考卷中,有關統計方面的試題更多關注時代熱點,如新農村建設、醫療衛生、藥品安全、質量檢測等.如2018年全國Ⅰ卷理科第3題就是典型的新時代新農村經濟建設問題,要求考生對現有數據進行分析與處理.

以頻率分布直方圖為背景考查離散型隨機變量的概率分布列與期望的計算,突出考查學生應用數學意識解決實際生活問題的能力.以莖葉圖為背景考查概率知識、2×2列聯表考查獨立性檢驗與概率知識等,這些問題著重考查學生從圖表中獲取信息、處理數據的能力.此類題在全國卷中多次出現,如2022年新高考Ⅰ卷第20題,以概率與統計模型為背景的創新題今后還會考查,值得我們關注.統計與函數相結合的概率統計題綜合性強、難度大,最近出現的一次是2017年全國課標Ⅲ卷第19題.純粹的統計學問題,如2016年全國課標Ⅲ卷文、理科第18題考查了生活垃圾無害化處理問題.

5 復習建議

概率與統計的知識點錯綜復雜又環環相扣,試題一般不是單獨考查某一個知識點,而是對多個知識點的綜合考查.因此在復習時,我們既要準確理解概念、公式與定理的含義,又要建構知識網絡,厘清概念、公式與定理之間的邏輯聯系.如概率的基本性質是基于事件關系這一個前提建立的,所以我們在學習概率的基本性質前必須理解隨機事件這一基本概念.如果弄不清事件的關系,那么就難以正確理解和運用概率的基本性質,同時也會影響對二項分布、超幾何分布的學習.

5.1 加強對概率、統計概念的精準理解,提升辨析概念的基本能力

概念是數學的細胞,是思維的載體,是創新的源泉.概念學習是學習數學的核心環節,整個數學知識體系是建立在概念基礎之上的.因此,我們要注重對統計與概率知識的再挖掘.深入理解統計學原理,領悟統計學思想,不能只停留在記住結論、公式上,要弄清結論所反映的原理是什么、公式又是如何推導的.高考中往往以“統計”為背景考查“概率”,因而概率知識是不可忽視的,概率題的突破可以從概率模型入手,分概率模型訓練.

5.2 重視閱讀理解訓練,培養數據處理及運算能力

圖表中信息的讀取、數據的處理是解決統計與概率問題的關鍵所在.在統計與概率試題中,一般題干文字較多、信息量較大、符號圖表密集、參考數據冗長.讀不懂題意是造成概率統計試題失分的主要原因之一,因此,我們要加強對閱讀理解的訓練,要學會三讀:一讀從統計圖表中能直接看到的信息,二讀經過簡單分析后能得到的信息,三讀超越數據本身的信息,在讀的過程中學會歸納、分析、總結、反思.

5.3 注重回歸教材與真題訓練,提高解決實際問題的應用能力

教材是教學之本,不少高考題的原型都源自于教材中的例題、習題.學生在復習中一定要注重對教材例題、習題的探究和利用,同時,還要加強對高考真題的適時訓練,并能從中發現試題的特點,悟出命題規律,進行有效復習.概率統計源自生產生活,同時又能解決生產生活中的實際問題.這些問題的設置要求考生對所給數據進行分析與處理,運用所學知識來解決實際問題,考查學生的應用能力.

(完)