強基計劃數學備考系列講座(12)
——組合計數

王慧興(正高級教師 特級教師)

(清華大學附屬中學)

組合計數是強基計劃校考的必考題目,但現行高中數學課標弱化了組合計數的教學要求.滿足于常態數學學習難以應對強基計劃校考,因此學生在強基備考時很有必要系統地掌握組合計數問題的探究、求解策略.

1 知識與技能

1.1 知識梳理

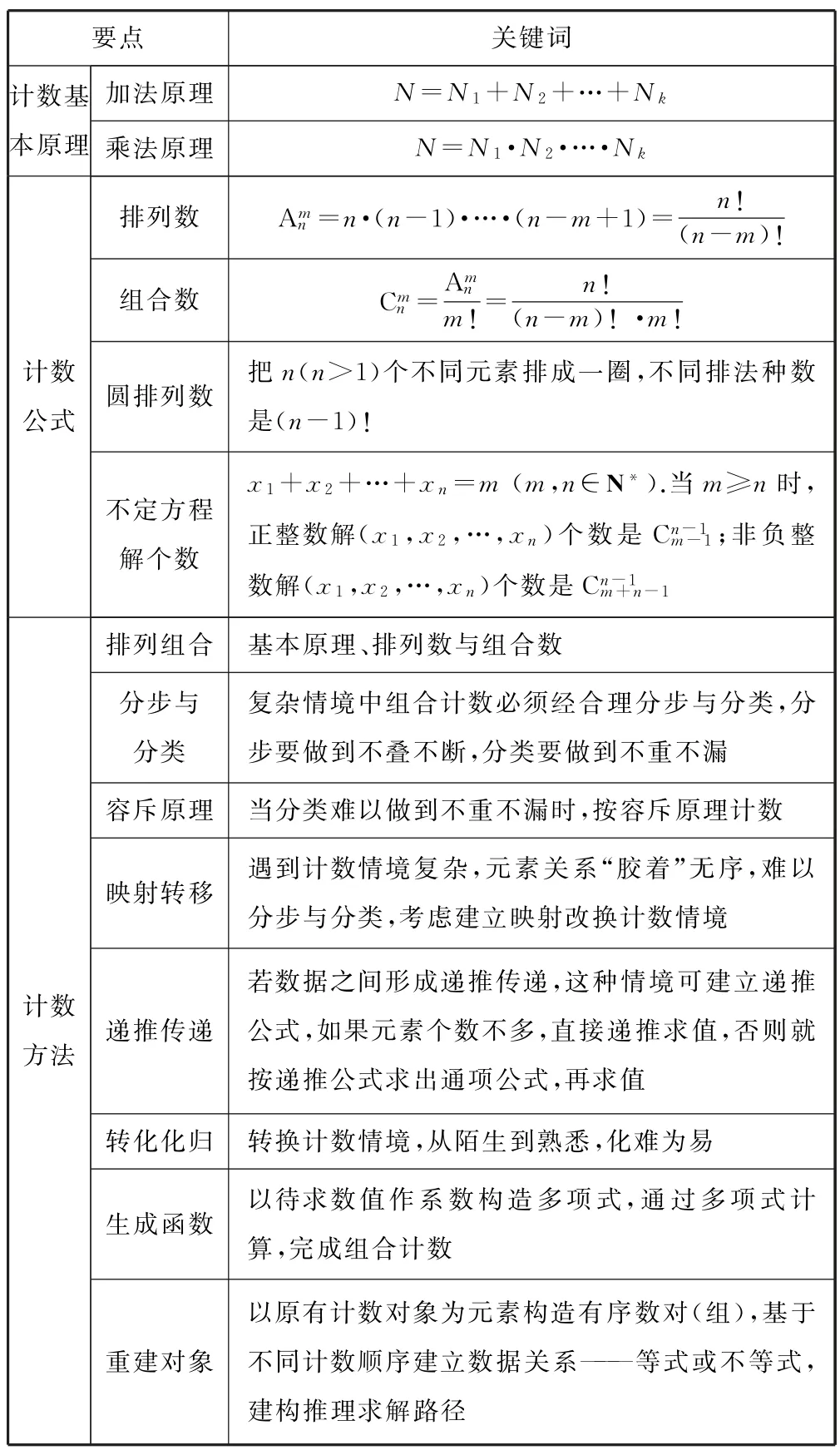
表1

1.2 要點解析

(1)滿足不定方程x1＋x2＋…＋xn＝m(m,n∈N?)的一個有序數組(x1,x2,…,xn),稱為其一個解,其正整數解(xi∈N?,i＝1,2,…,n)與非負整數解(xi∈N,i＝1,2,…,n)可以相互轉化.現探求其正整數解個數,這里先給出一種求法——插板法.

把m＝1＋1＋…＋1想象成沒有區別的m個小球,把變量x1,x2,…,xn想象成n個不同的盒子,轉化為求把這m個相同的小球裝入n個不同的盒子里的不同裝法數.

我們先把m個相同的小球排成一行,只有1種方法,再從m－1個空隙里任選n－1個空隙插入沒有區別的隔板,把小球分成n段,最后逐段依次定序裝入n個盒子里,這種不同裝法數就等于分段方法數,因此,按照方程對變量x1,x2,…,xn賦值得到的方程的正整數解(x1,x2,…,xn)個數就是,其中m＞n.

對方程x1＋x2＋…＋xn＝m的任一非負整數解(x1,x2,…,xn),由x1＋x2＋… ＋xn＝m,得(x1＋1)＋(x2＋1)＋…＋(xn＋1)＝m＋n,令xi＋1＝yi(i＝1,2,…,n),則(x1＋1,x2＋1,…,xn＋1)就是方程y1＋y2＋…＋yn＝m＋n的一個正整數解.這就給出原方程的非負整數解與新方程的正整數解之間的一一對應關系,所以原方程的非負整數解的個數是

(2)容斥原理:有限集合X的元素個數記作|X|,則n個有限集合Ai(1≤i≤n)的并集元素個數算法為

這個算法稱為容斥原理,當其中任意兩個集合交集都是空集時,就是加法原理.

(3)映射轉移:兩個有限集合A,B之間的映射f:A→B,如果f是單射,則|A|≤|B|;如果f是滿射,則|A|≥|B|;如果f是雙射,則|A|＝|B|;倍數映射——B中每個元素在A中都恰有k個原像,則|A|＝k|B|.

(4)轉化化歸:情境轉化是組合計數常態,通過情境轉化,在新情境中計數對象之間邏輯關系清晰,使得分步、分類變得容易,便于整體把握,從根本上化難為易.“轉化化歸”是一種思想、觀點,“映射轉移”就是一種典型的具體策略,“插板法”又是映射轉移方法的一種具體表現.由于計數情境的多樣性,轉化化歸不僅表現多樣,而且往往富有技巧性.下面再給出探究上述不定方程兩類解的個數的另一種轉化方法.

記方程x1＋x2＋…＋xn＝m(m＞n)的所有正整數解構成集合A.任取(x1,x2,…,xn)∈A,則

換元,令(x1,x1＋x2,…,x1＋x2＋…＋xn－1)＝(y1,y2,…,yn－1),則得到一個定序排列1≤y1＜y2＜…＜yn－1≤m－1,記所有這種定序排列的集合為B,則這種換元建立了一個雙射f:A→B,故方程的正整數解的個數為

記x1＋x2＋…＋xn＝m的所有非負整數解構成一個集合A′,任取(x1,x2,…,xn)∈A′,則

等價轉化為

換元,令x1＋x2＋…＋xi＋i－1＝yi(1≤i≤n－1),得1≤y1＜y2＜…＜yn－1≤m＋n－1,所有這種定序排列構成的集合記作B′,得到雙射f:A′→B′,故上述方程的非負整數解的個數為

(5)生成函數:又稱母函數,把計數方法與特定多項式中某種項形成對應,但通常是多對一,甚至是所有方法與同一種項對應,因此所求計數結果等于所構造的多項式中對應項的系數.因此,母函數方法本質上也是轉化化歸思想的一種具體表現.讀者可結合下文例15理解.

2 典例精析

2.1 計數基本技能

計數對象之間關聯簡單,計數邏輯清晰,分步與分類簡單易行,歷練這些方法是促進思維進階、發展計數高階思維必經環節.

1)窮舉法

窮舉法是一項基本技能,常用于元素不多的情境中.古典概型概率計算本質上是兩個計數之比,但現行高中數學課標卻要求先學習古典概型,后續再學習排列組合,就是強調教學必須重視引領學生歷練、掌握窮舉法.

例16位同學在畢業聚會活動中進行紀念品的交換,任意兩位同學之間最多交換一次,進行交換的兩位同學互贈一份紀念品.已知6位同學之間共進行了13 次交換,則收到4 份紀念品的同學人數為( ).

A.1或3 B.1或4 C.2或3 D.2或4

由于|V|＝6,稱圖G(V,E)為6階簡單圖,如果其中每兩個頂點之間都連一條邊,則稱之為完全圖,記作K6,其邊數應當是,但這里|E|＝13,所以圖G(V,E)可以從完全圖K6中去掉兩條邊得到,而去掉兩條邊的方式有兩種,如圖1所示.

圖1

在圖1-甲中,從K6中刪除有公共頂點的兩條邊A1A3,A1A5,得到圖G(V,E),其度數(每個頂點引出的邊的條數)序列為(d1,d2,d3,d4,d5,d6)＝(3,5,4,5,4,5);在圖1-乙中從K6中刪除無公共頂點的兩條邊A1A3,A2A4,得到圖G(V,E),其度數序列為(d1,d2,d3,d4,d5,d6)＝(4,4,4,4,5,5).

綜上,本題5階簡單圖G(V,E)中度數是4的點數是2或4,故選D.

2)先組合后排列

例2安排3名志愿者完成4項工作,每人至少完成1項,每項工作由1人完成,則不同的安排方式共有( ).

A.12種 B.18種 C.24種 D.36種

3)特殊元素優先安排

例3用0,1,…,9十個數字,可以組成有重復數字的三位數的個數為( ).

A.243 B.252 C.261 D.279

4)相鄰元素捆綁處理

例4把5件不同產品擺成一排.若產品A與產品B相鄰,且產品A與產品C不相鄰,則不同的擺法有_________種.

第一步,捆綁A,B整合成一個“新產品”的方法數是;第二步,把C之外的2件產品與“新產品”排成一列的方法數是;第三步,再把產品C插入已排好的4件產品之間的方法數都是(無論A在何處)種方法.由分步乘法原理,滿足題意的5件產品擺放方法數是

5)隔離問題插空處理

例5某次聯歡會要安排3個歌舞類節目、2個小品類節目和1個相聲類節目的演出順序,則同類節目不相鄰的排法種數是( ).

A.72 B.120 C.144 D.168

第一類,把2個小品類節目與1個相聲類節目排入3個舞蹈節目的兩個空隙與兩端之一,共有種方法.

第二類,把1個相聲節目與兩個小品類節目之一重組在一起使之相鄰,重組的方法共有,再以兩個元素排入3個舞蹈節目之間的兩個空隙有種插入方法,這一類不同方法數是.

6)分排問題直排處理

例6如圖2所示,在一次射擊比賽中,有8個泥質靶子掛成3列,一位神槍手按如下規則打掉所有靶子:首先選擇將要有一個靶子被打掉的一列;然后在被選列中打掉尚存的最下面一個靶子.求打掉這8個靶子共有多少種不同的順序.

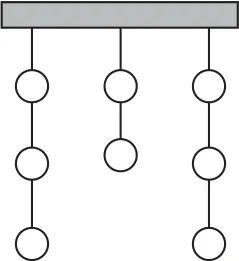
圖2

7)正難則反,轉化情境

例7把5件不同產品擺成一排.若產品A與產品B相鄰,且產品A與產品C不相鄰,則不同的擺法有________種.

因為A,B已經相鄰,所以總控數據匯總C與A相鄰的情形一定是B位于A,C之間的ABC或CAB兩種固定結構,以這兩種固定結構之一與另外兩個自由產品任意排成一列的擺法是,所以總控數據中A與C相鄰的擺法是.

綜上,分離出滿足題設條件的產品擺法是

2.2 分步與分類

計數對象之間“膠著糾纏”“不獨立”,難以用一個組合數或排列數直接給出算法,分步與分類就成為求解組合計數問題的常態技能.

例8定義“規范01數列”{an}如下:{an}共有2m項,其中m項為0,m項為1,且對任意k≤2m,a1,a2,…,ak中0的個數不少于1的個數.若m＝4,則不同的“規范01數列”共有( ).

A.18個 B.16個 C.14個 D.12個

第一類,前4項都是0,后4項都是1,這樣的“規范01數列”個數只有1個.

第二類,前4項中a2,a3,a4恰有1個1,后4項中a5,a6,a7恰有1個0,這樣的“規范01數列”個數是

第三類,前4項中恰有2個1,這2 個1 只能是a2＝a4＝1或a3＝a4＝1,因此,前4項安排方法數是;后4項中恰有2個0,這2個0只能是a5＝a6＝0或a5＝a7＝0,后4項安排方法數是,因此,這樣的“規范01數列”個數是

綜上,由分類加法原理,滿足題設條件的“規范01數列”個數是,故選C.

例9(北京大學)將不大于12的正整數分為6個兩兩交集為空集的二元集合,并且每個集合中的兩個元素互質,則不同的分法有________種.

因為C＝{2,4,6,8,10,12}中任意兩個元素都不互質,所以這6個數分別屬于6個不同的子集,記

其中i∈Ai(i∈C).其余元素1,7,11可以任意放入每一個子集中,但5?A10,3和9?A6∪A12.分類計數:

情形一,5∈A6∪A12,這時3 和9∈A2∪A4∪A8∪A10,1,7,11 任意放,所以這一類的劃分個數為

情形二,5?A6∪A12,則5∈A2∪A4∪A8,3和9含于A2,A4,A8不含5的另外2個連同A10之中,1,7,11可以任意放,所以這一類劃分的個數為

2.3 容斥計數

例10(上海交通大學)在小于1000的正整數中,既不是5 的倍數也不是7 的倍數的整數個數是________.

2.4 映射轉移

計數對象之間“膠著”,關聯性強,算法邏輯不清晰,計數情境轉換就成為探求復雜計數問題的方法.

例11(清華大學)已知集合A,B,C?{1,2,…,2020},且A?B?C,則有序集合組(A,B,C)的個數是________.

由分步乘法原理,這種映射的個數是42020,所以滿足題設條件的有序集組(A,B,C)的個數是42020.

2.5 遞推傳遞

例12(中國科學技術大學)設k(k≥3)個人進行互相傳球游戲,每個拿球的人等可能地把球傳給其他人中的任何一位.若初始時,球在甲手中,則第n次傳球后,球又回到甲手中的概率為________.

2.6 重建模型

重建模型是積極地改進算法,追求更為快捷、清晰的算法的永恒追求,也是映射轉移計數的一種具體表現.

例13(上海交通大學)兩條異面直線稱為一個異面直線對,連接正方體的8個頂點得到的所有直線中,異面直線對的個數是_________.

因為任一四面體ABCD的六條棱都可以構成3個異面直線對“AB與CD、AC與BD、AD與BC”,而從正方體的8個頂點中任取4個頂點所得的個四點組中共有個不共面四點組,這些四點組都可以作為四面體的四個頂點,也就是四面體的個數,故所求異面直線對個數是

下面用古典概型計算幾何概型,這是基于對稱性處理重建模型、改善計數情境轉化的一種常用策略.

例14(中國科學技術大學)在圓周上獨立隨機取n個點,求此n個點可被半圓周覆蓋的概率P.

2.7 生成函數

例15(上海交通大學)從2個紅色球、3個黑色球、5個白色球(同色球完全相同)中任意取出6個,則不同取法種數是________.

因為展開式通項為xixjxk,其中i∈{0,1,2},j∈{0,1,2,3},k∈{0,1,2,3,4,5},所以x6的系數就是方程i＋j＋k＝6滿足條件“i≤2,j≤3,k≤5”的非負整數解(i,j,k)的個數.

按i∈{0,1,2}枚舉可得這種有序非負整數三元組(i,j,k)的個數是3＋4＋4＝11,故滿足題設條件取出6個球的方法數是11.

2.8 化歸轉化

例16(清華大學)給定一個圓周上十個等分點Ai(1≤i≤10),則取其中的四個,得到等腰梯形的四個頂點的取法數是( ).

A.60 B.45 C.40 D.50

上面定義的正整數有序三元組(x,y,z)由條件確定,枚舉可得所有(x,y,z)共有6個:(1,1,7),(2,1,6),(3,1,5),(1,2,5),(2,2,4),(1,3,3),所以可以得到等腰梯形四個頂點的取法數是10×6＝60,故選A.

例17(復旦大學)方程18x＋4y＋9z＝2021的正整數解(x,y,z)的個數是________.

模9,得4y≡5(mod9),即y≡－1(mod9),y＝9y′－1(y′∈N?),所以原方程化為18x＋4(9y′－1)＋9z＝2021 ?2x＋4y′＋z＝225,從而z是奇數,記z＝2z′－1(z′∈N?),方程繼續轉化為x＋2y′＋z′＝113,從而x＋z′必為奇數,即x,z′一奇一偶,由對稱性,這兩種情形的解數一樣多.

不妨設x是奇數,記x＝2x′－1,z′＝2z″(x′,z″∈N?),繼續轉化上述方程,得x′＋y′＋z″＝57,該方程的正整數解(x′,y′,z″)的個數是,對應地確定個原方程的正整數解(x,y,z)＝(2x′－1,9y′－1,4z″－1),故原方程的正整數解(x,y,z)個數是

2.9 換序計數

例18給定正整數n,集合S＝{1,2,…,10}的所有有序子集組(A1,A2,…,An)構成一個集合T,則的值是_________.

另一方面,對任一a∈S,含這個a的所有有序子集組(A1,A2,…,An)的個數是

因此,所有n＋1元組(A1,A2,…,An,a)的個數為

由①②,得

3 實戰演練

1.從1,3,5,7,9中任取2個數字,從0,2,4,6中任取2個數字,一共可以組成_________個沒有重復數字的四位數(用數字作答).

2.把5個不同的小球裝入4個不同的盒子,要求每個盒子至少裝入1個球,則不同裝法有________種.

3.某臺小型晚會由6個節目組成,演出順序有如下要求:節目甲必須排在前兩位,節目乙不能排在第一位,節目丙必須排在最后一位,該臺晚會節目演出順序的編排方案共有( ).

A.36種 B.42種 C.48種 D.54種

4.(北京大學)已知五項正整數數列{an}:a1,a2,a3,a4,a5,滿足|ak＋1－ak|≤1(k＝1,2,3,4),其中存在一項的值是3,則這種數列的個數為_________.

5.(復旦大學)某公司安排甲、乙、丙等7人完成7天的值班任務,每人負責1天.已知甲不安排在第一天,乙不安排在第二天,甲和丙安排在相鄰兩天,則不同安排方式的種數是_________.

6.(上海交通大學)2 條拋物線最多分平面為7份,3條最多分16份,則4條拋物線最多把平面分成_________份.

7.(復旦大學)方程3x＋4y＋12z＝2020的非負整數解(x,y,z)的個數是________.

8.(北京大學)如果一個十位數F的各位數字之和等于81,則稱F為一個“好數”,則所有好數的個數為________.

9.(北京大學)現有7把鑰匙,用這些鑰匙隨機開鎖,則D1,D2,D3這三把鑰匙不能打開對應的鎖的概率是_________.

10.(北京大學)從一個六元集合到一個三元集合的滿射個數是________.

答案1.1260. 2.240. 3.B. 4.211. 5.1128 .6.29. 7.14365. 8.48619. 9.

(完)