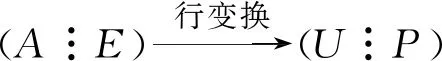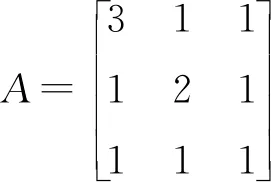矩陣分解思想解題意義探究
——高等代數北大第五版
孫銘均
(遼寧師范大學 116000)
數學家在探索線性方程時曾發現解方程的規律,即方程組的解只跟未知量系數及常數項有關,與其它的內容無關,于是提出將方程組的系數及常數項單獨提煉出來,寫成一個整齊的數據表,而這一數據表用括號表示出來,就是矩陣分解的來源.本次研究首先從矩陣分解的思想角度說明它如何簡化了大型線性方程組的計算,然后從矩陣的和式分解及應用和矩陣的乘積分解及應用說明如何有針對性地應用矩陣分解的思想解決特定約束條件下大型線性方程組問題的方法.
1 矩陣分解概述
定義:設
將這兩個s×n矩陣相加,則可得
C=(cij)=(aij+bij)sn
兩個矩陣相加的和可以記為C=A+B.
矩陣的和式分解就是將以上相加的過程逆推過來,呈現C=A+B的矩陣分解后的矩陣和原矩陣是相同的.
2 矩陣的和式分解及應用
2.1 矩陣的和式分解
定理1:任意一個n×n矩陣都可表示為一對稱矩陣與一反對稱矩陣之和.
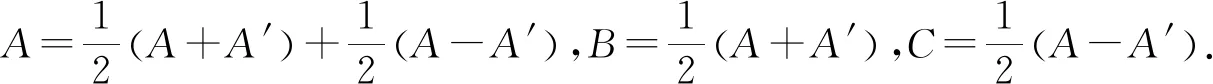
定理2:秩等于r的對稱矩陣可以表成r個秩等于1的對稱矩陣之和.
證明:設A是秩為r的n階實對稱矩陣,那么存在可逆矩陣P,使得

2.2 矩陣和式分解的應用
現在假設一個矩陣A可以分解成兩個或兩個以上矩陣的和的形式,那么就能夠應用這種方式來計算與該矩陣A可交換的矩陣,及矩陣A的方冪等.

3 矩陣的乘積分解及應用
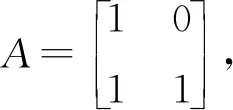
3.1 矩陣的LU分解及應用
LU分解:設A=(aij)是n階可逆矩陣,假設A的對角線下(上)方的元素全為零,那么即可視為當i>j時,aij=0(當i 定理3:LU分解定理 設A是n階可逆矩陣,那么可知存在唯一的單位下三角矩陣L和上三角矩陣U,A=LU的充分必要條件是A的所有順序主子式均非零,那么可得: 解1應用上面的定理對矩陣(A?E)作初等行變換可得 由以上的案例可以看到矩陣的和式分解的應用思想,就是把一個較為復雜的線性方程,以把它變成矩陣的方式,把方程結構變得簡單,讓它降冪降次以令數學計算簡化;而矩陣的乘積分解的思路,就是利用矩陣分解過程中條件的約束和計算的關系來構建新的矩陣,而這個矩陣是一個簡化了的,能夠反映出已知條件和解關聯特征的方程.