二重積分概念與性質課程思政教學設計

鄧明香 馮永平

(廣東省廣州大學數學與信息科學學院 510006)

二重積分是多元函數微積分學應用的一個主要內容,是在解決實際問題的實踐中不斷抽象出來的,是一元函數定積分、多元函數曲線積分的推廣.結合課程思政相關元素,本文主要從學情分析、教學目標、教學方法、教學策略、教學設計幾方面探討了二重積分的概念教學中如何隱性地融入課程思政元素,達到教書育人的目的.

1 學情分析及教學目標分析

本節課程選自理工類專業必修課《高等數學Ⅱ2》,為一節新授課程, 第8章《二重積分》第1節“二重積分的概念與性質”,教材選用林偉初，郭安學,高等數學(經管類下冊，第1版),北京大學出版社,2018.07, 面向我校一流專業地理科學專業 211、212、213班開設.

本節課程學習前,學生已掌握了一些規則立體圖形的體積求法,如長方體、圓柱體、錐體等;已學完一元微積分學、空間解析幾何及多元函數的微分學等高等數學內容;掌握了定積分概念及相關數學思想,能熟練使用分割、近似、求和、取極限四個步驟求解曲邊梯形面積問題.在學習中，學生對推廣后的求解曲頂柱體體積問題能給出粗略方案,但精確化比較困難,特別是對最后如何從近似轉向精確的極限手法難以理解;學生對概念中涉及的積分區域和重積分符號的抽象性和復雜性有畏懼感,容易排斥抽象的概念課.

本節課程的教學目標為以下幾個方面.

知識與能力方面：掌握二重積分的概念、性質; 學會用極限思想分析具體問題,能靈活使用“分割,近似,求和,取極限”處理二元函數的相關問題;掌握從實例形成概念定義的重要方法.

過程與方法方面：通過類比定積分,引導學生回顧“以直代曲”在解決定積分問題中起到的關鍵作用,為整節課架設一個基本思維框架,讓學生明確學習內容;借助熟悉的“頂面為平面的體積計算問題”“密度均勻分布平面薄片質量計算問題”,引導學生學會從特殊到一般,從具體到抽象的數學方法,實現能力目標的培養.

情感方面：借助引例直觀體會“以直代曲”和“逼近”的思想,學習歸納、類比的推理方式,體驗從特殊到一般、從具體到抽象、化歸與轉化的數學思想;從實踐中創設情境,滲透“化整為零、積零為整”的辨證唯物觀,培養學生的創新意識和科技服務于生活的人文精神.

本課程用“問題驅動”教學理念的統領指導實施課程教學,力求在課程教學中實現培養學生具備“用數學的眼光觀察世界, 用數學的思維分析世界,用數學的語言表達實現世界”的最終能力素養目標.

2 教學過程

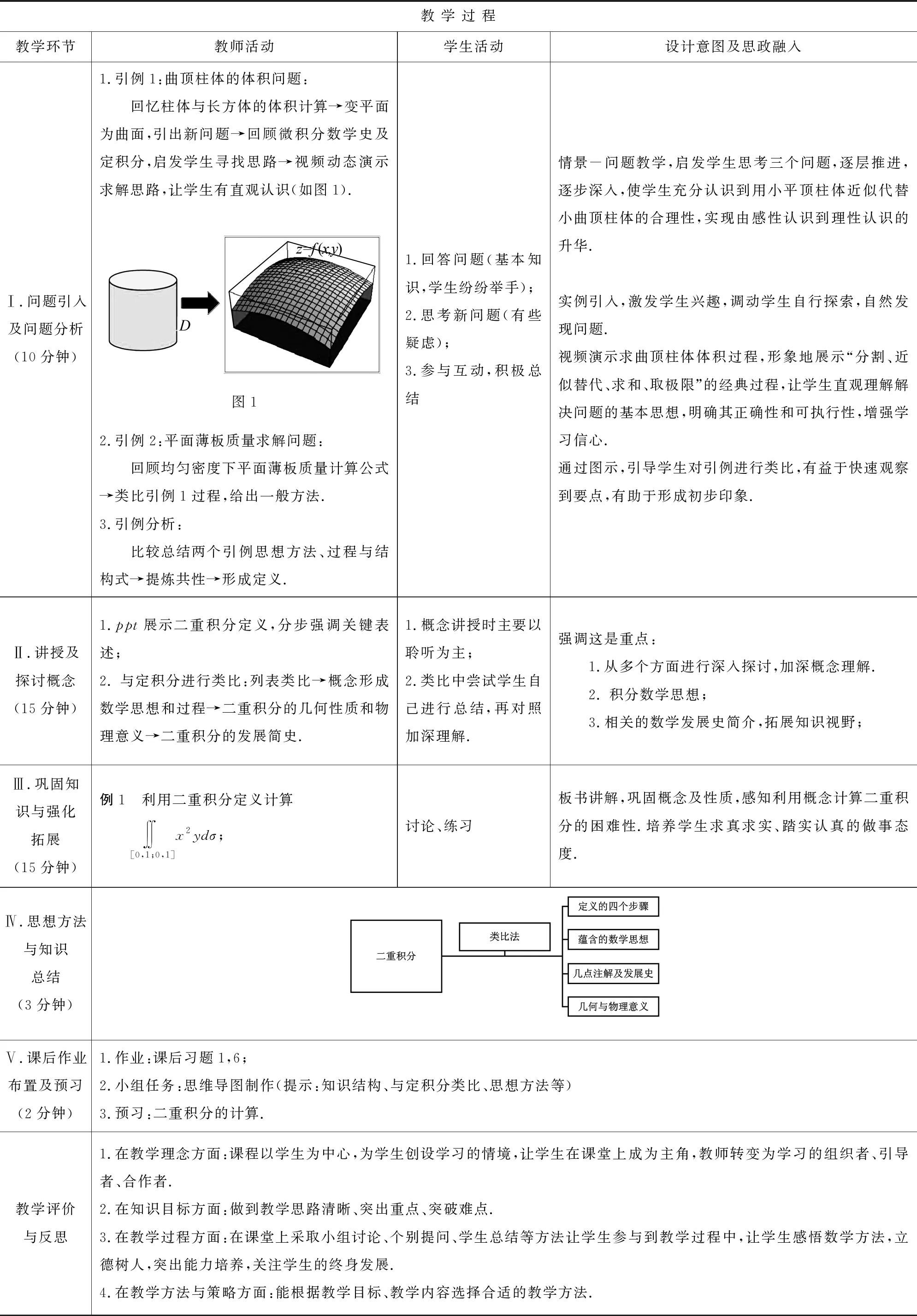
教 學 過 程教學環節教師活動學生活動設計意圖及思政融入Ⅰ.問題引入及問題分析(10分鐘)圖11.引例1:曲頂柱體的體積問題:回憶柱體與長方體的體積計算→變平面為曲面,引出新問題→回顧微積分數學史及定積分,啟發學生尋找思路→視頻動態演示求解思路,讓學生有直觀認識(如圖1). 2.引例2:平面薄板質量求解問題:回顧均勻密度下平面薄板質量計算公式→類比引例1過程,給出一般方法.3.引例分析:比較總結兩個引例思想方法、過程與結構式→提煉共性→形成定義.1.回答問題(基本知識,學生紛紛舉手);2.思考新問題(有些疑慮);3.參與互動,積極總結情景-問題教學,啟發學生思考三個問題,逐層推進,逐步深入,使學生充分認識到用小平頂柱體近似代替小曲頂柱體的合理性,實現由感性認識到理性認識的升華.實例引入,激發學生興趣,調動學生自行探索,自然發現問題.視頻演示求曲頂柱體體積過程,形象地展示“分割、近似替代、求和、取極限”的經典過程,讓學生直觀理解解決問題的基本思想,明確其正確性和可執行性,增強學習信心.通過圖示,引導學生對引例進行類比,有益于快速觀察到要點,有助于形成初步印象.Ⅱ.講授及探討概念(15分鐘)1.ppt展示二重積分定義,分步強調關鍵表述;2. 與定積分進行類比:列表類比→概念形成數學思想和過程→二重積分的幾何性質和物理意義→二重積分的發展簡史.1.概念講授時主要以聆聽為主;2.類比中嘗試學生自己進行總結,再對照加深理解.強調這是重點:1.從多個方面進行深入探討,加深概念理解.2. 積分數學思想;3.相關的數學發展史簡介,拓展知識視野;Ⅲ.鞏固知識與強化拓展(15分鐘)例1 利用二重積分定義計算?[0,1;0,1]x2ydσ;討論、練習板書講解,鞏固概念及性質,感知利用概念計算二重積分的困難性.培養學生求真求實、踏實認真的做事態度.Ⅳ.思想方法與知識總結(3分鐘)Ⅴ.課后作業布置及預習(2分鐘)1.作業:課后習題1,6;2.小組任務:思維導圖制作(提示:知識結構、與定積分類比、思想方法等) 3.預習:二重積分的計算.教學評價與反思1.在教學理念方面:課程以學生為中心,為學生創設學習的情境,讓學生在課堂上成為主角,教師轉變為學習的組織者、引導者、合作者.2.在知識目標方面:做到教學思路清晰、突出重點、突破難點.3.在教學過程方面:在課堂上采取小組討論、個別提問、學生總結等方法讓學生參與到教學過程中,讓學生感悟數學方法,立德樹人,突出能力培養,關注學生的終身發展.4.在教學方法與策略方面:能根據教學目標、教學內容選擇合適的教學方法.