微溝槽織構對膨脹錐摩擦性能影響的數值模擬*
王鑫 郭慧娟 徐丙貴 趙運才 王宏偉 鄭彬
(1. 江西理工大學機電工程學院 2. 中國石油集團工程技術研究院有限公司 3.攀枝花學院智能制造學院)
0 引 言
膨脹錐作為膨脹管技術(SET)的主要工具之一,在膨脹過程中表面受到極大的接觸應力。在超長段膨脹管膨脹過程中,膨脹錐表面將逐漸被磨損,其最大有效膨脹直徑將縮小,導致膨脹管膨脹后內徑達不到要求,影響后續鉆采作業[1-2]。在膨脹過程中,膨脹錐表面漸進性磨損發生在膨脹錐膨脹區。該磨損涉及接觸面之間的機械和化學相互作用,在很大程度上受潤滑狀態、膨脹速度、膨脹錐和膨脹管材料硬度的影響[3-5]。因膨脹錐表面受力極大,在確保膨脹率的前提下,膨脹錐的材質、錐角及表面形貌等因素對自身摩擦性能有重要影響。在膨脹管管材、膨脹錐結構和選材都確定的前提下,影響膨脹錐摩擦性能的主要因素是界面接觸狀態和接觸壓力。界面接觸狀態受潤滑液/潤滑脂和接觸表面形貌影響,而接觸壓力受膨脹管材料力學性能影響。
目前對膨脹錐減摩耐磨研究從潤滑機理和表面涂層技術入手取得了較多成果。劉強等[6]采用摩擦模擬試驗的方法,研究二硫化鉬鋰基脂、鉛基潤滑脂和沒有潤滑脂的3種條件下普通 N80膨脹管材料的摩擦性能;試驗結果表明,在有潤滑脂存在的條件下,膨脹管膨脹過程中的摩擦因數和磨損量會顯著降低,并且磨損機理由磨粒磨損變為黏著磨損。魏松波等[7]采用噴涂技術在膨脹錐部分表面制備厚度約為 200 μm的碳化物硬質涂層,通過摩擦磨損試驗研究涂層和無涂層試樣的摩擦性能;結果表明,硬質涂層可以明顯減小試樣的摩擦力,減輕試樣的表面磨損。
傳統機械觀點認為,兩摩擦副接觸表面越光滑摩擦因數越小,所以摩擦力和磨損率也會減小。但學者們對仿生學的研究表明,相比光滑表面,具備一定非光滑特征的摩擦表面具備更好的摩擦特性,即摩擦副接觸表面并非越光滑越好。近年來,通過機械加工、電解、激光等方式在摩擦副表面加工表面微織構實現減摩耐磨開展了眾多研究,理論和試驗結果都顯現出微織構在減摩耐磨上有突出優點。DENG J.X.等[8]對WC/Co硬質合金刀具前刀面進行不同幾何特征的表面織構分析,并在織構后刀面上填充二硫化鉬固體潤滑劑,通過織構化刀具和常規刀具干切削對比試驗驗證織構性能;結果表明,與傳統加工方法相比,前刀面織構化后的刀具,其工作時的切削力、切削溫度以及刀屑界面摩擦因數均顯著降低。赫冬等[9]為了研究微織構幾何形貌及排布方式對發動機氣缸套摩擦副減摩耐磨的作用,采用激光加工技術在CKS活塞環上進行微織構化處理;通過摩擦磨損試驗得出活塞環表面微織構可改善摩擦磨損性能,減小磨損率;其原因是微織構能儲存潤滑油、收集磨屑以及減小活塞環和氣缸套的接觸面積。
目前評價膨脹管技術主要從膨脹管膨脹質量上來考慮,忽略了對膨脹錐摩擦性能的分析。筆者首先根據膨脹管彈塑性理論,建立膨脹錐受力模型,再進行無織構膨脹錐的膨脹過程有限元模擬,旨在分析無織構膨脹錐的摩擦性能,為后續織構化膨脹錐分析提供參考對比。因當前將織構應用到膨脹錐表面來增強其耐磨性的研究還較少,筆者通過有限元的方法對微溝槽膨脹錐進行了膨脹模擬。微溝槽形狀是三角溝槽,相對于傳統圓形、方形等微織構,三角微溝槽織構可以產生較好的楔形效應[10-11]。所研究的微溝槽織構是45°斜線走向溝槽和正弦型走向溝槽。筆者通過比較無織構與織構化膨脹錐模擬結果,從應力角度分析表面微溝槽織構膨脹錐的干摩擦性能,以期為膨脹錐減磨研究應用表面微溝槽織構提供理論依據。
1 膨脹錐受力模型
1.1 膨脹管彈塑性力學分析
在膨脹過程中,隨著內壓的逐漸增大,膨脹管先進入彈性階段,然后是彈塑性階段,最后是塑性流動,發生塑性變形[12]。在該過程中,膨脹錐受到膨脹管的反作用力是不連續變化量,難以用具體解析式表達。取膨脹管外壁剛進入塑性變形狀態為研究對象,在該時刻膨脹錐受到膨脹管的反作用力最大。在膨脹管剛進入塑性變形區域內縱向取一厚度為dz的微單元截面,進行彈塑性力學分析。膨脹管微單元受力示意圖如圖1所示。
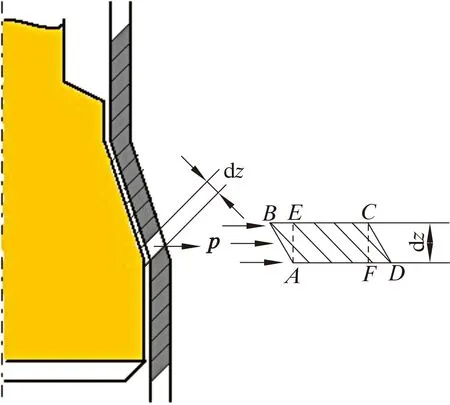
圖1 膨脹管微單元受力示意圖Fig.1 Force diagram of an infinitesimal element of the expansion cone
由于膨脹錐的硬度遠大于膨脹管,在分析過程中,假定膨脹錐的屈服強度遠大于膨脹管的屈服強度,即膨脹錐的變形不予考慮,兩者間的接觸方式視為面-面接觸。對膨脹管做如下假定:①材質具有各向同性,材料為理想彈塑性體,即材料沒有加工硬化,符合理想彈塑性體的應力應變曲線;②為理想的同心圓管,壁厚均勻,橫截面為滾圓;③在每一個橫截面周向方向內,應力分布均勻[13]。
膨脹錐在推力作用下與膨脹管接觸,接觸正壓力產生壓力p,其作用于膨脹管內壁,使膨脹管徑向膨脹。可將AB邊受壓力p作用的四邊形ABCD等效為AE邊承受均布壓力p作用的四邊形AECF。
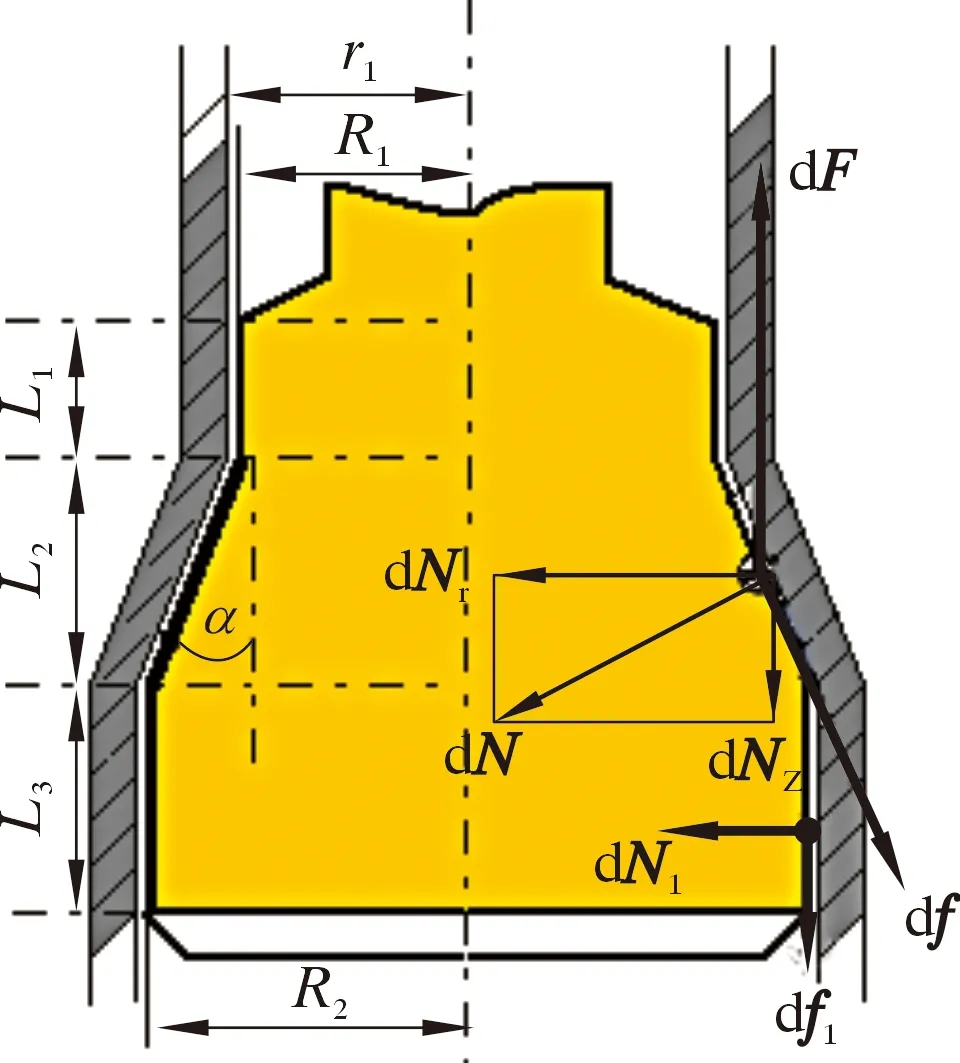
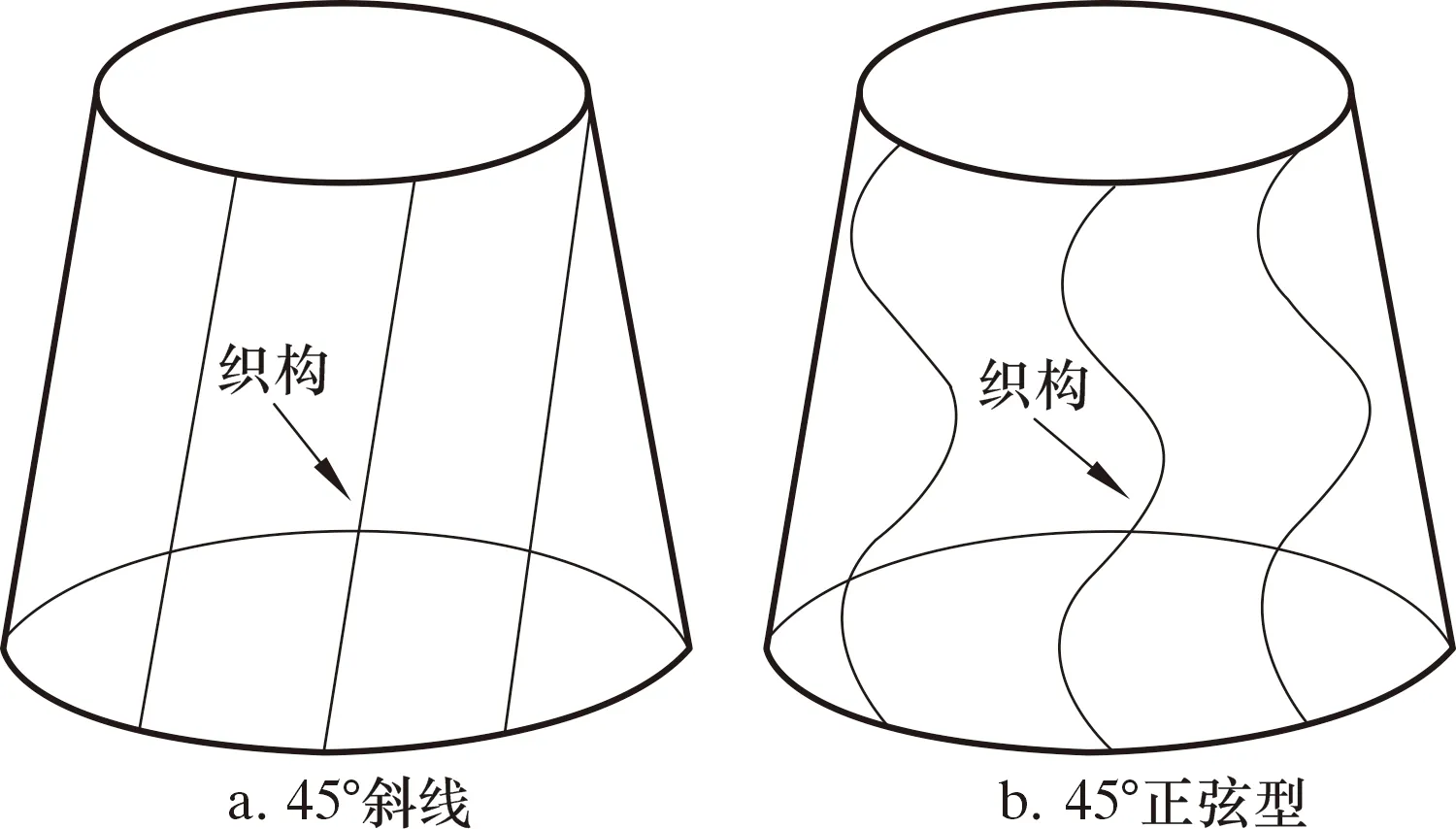
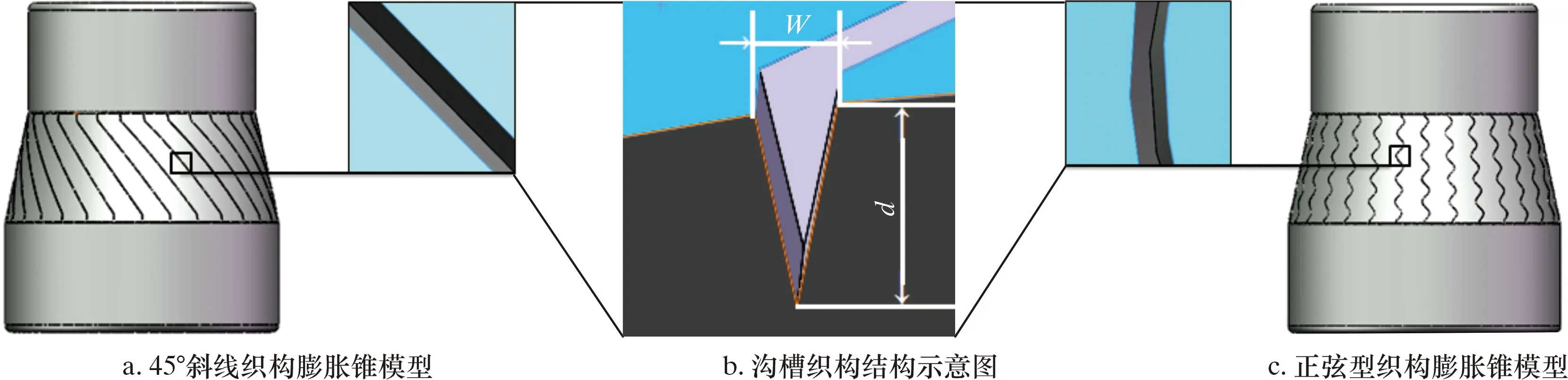
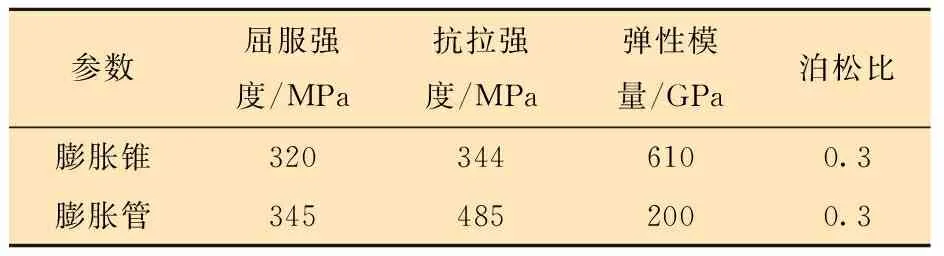
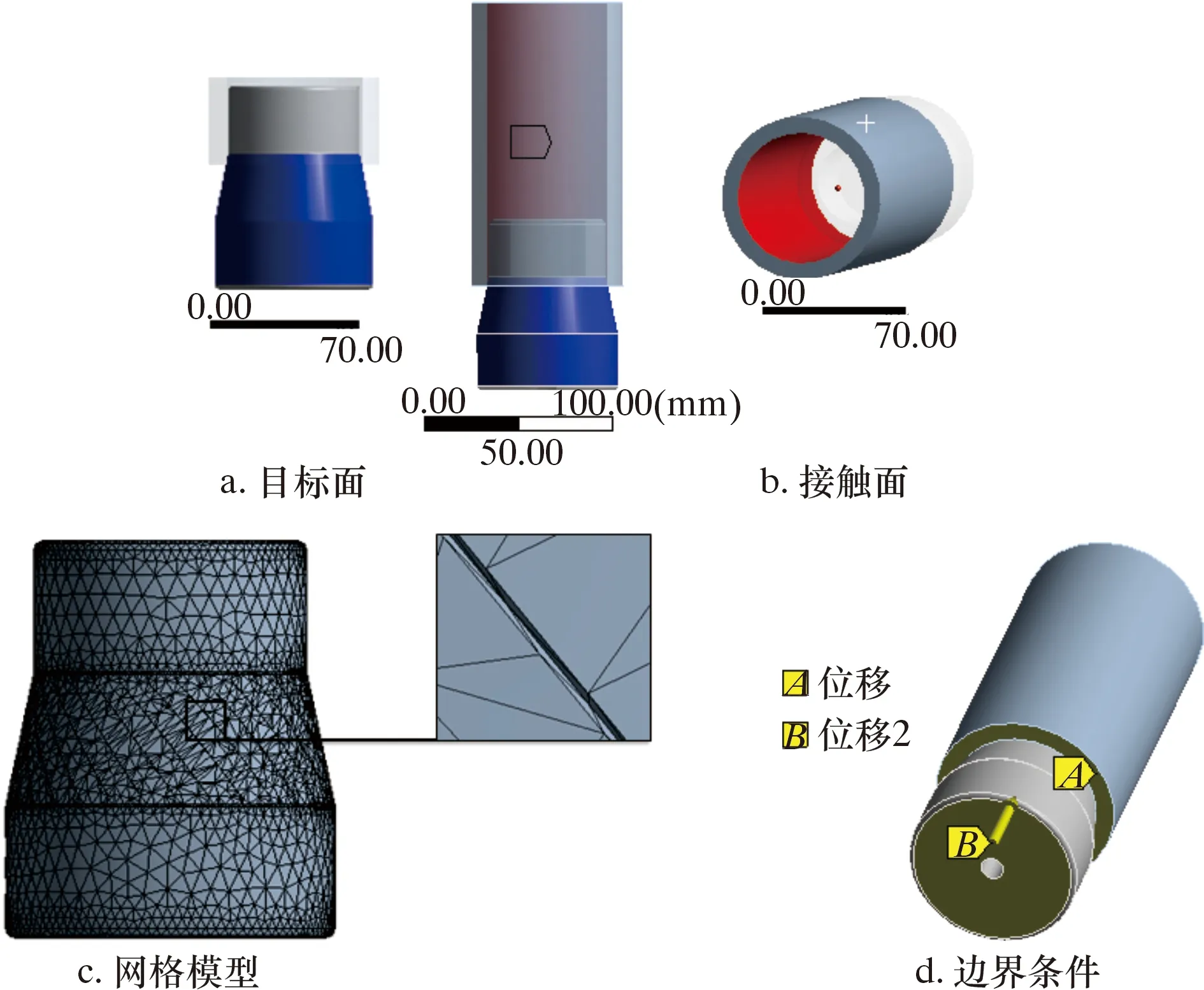
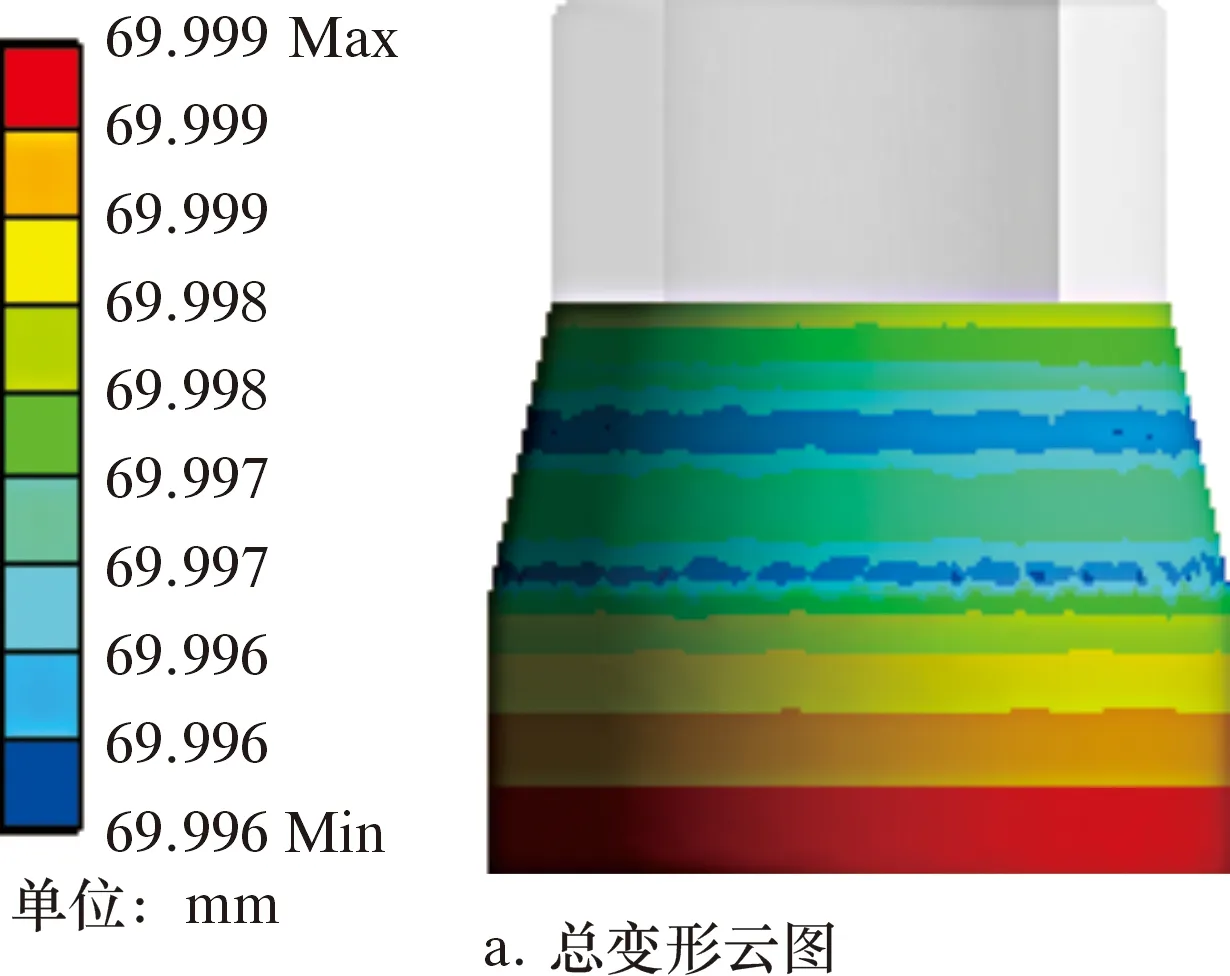
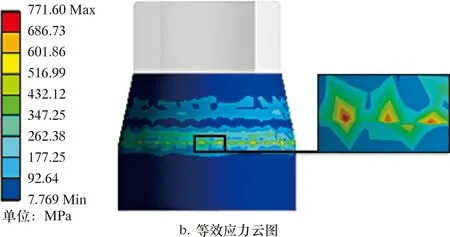
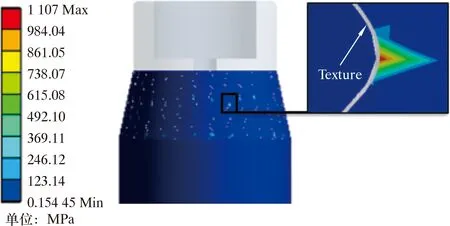
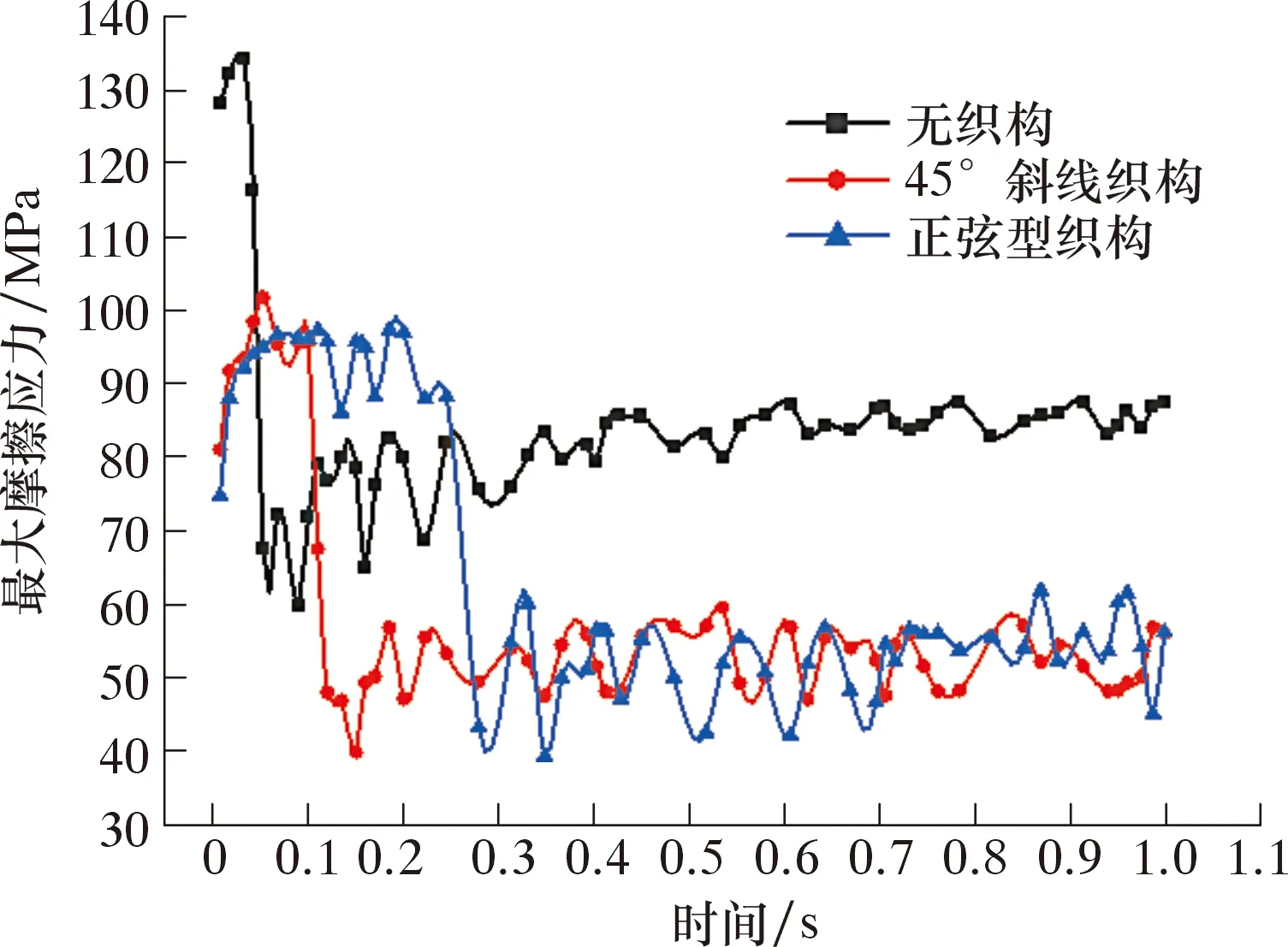
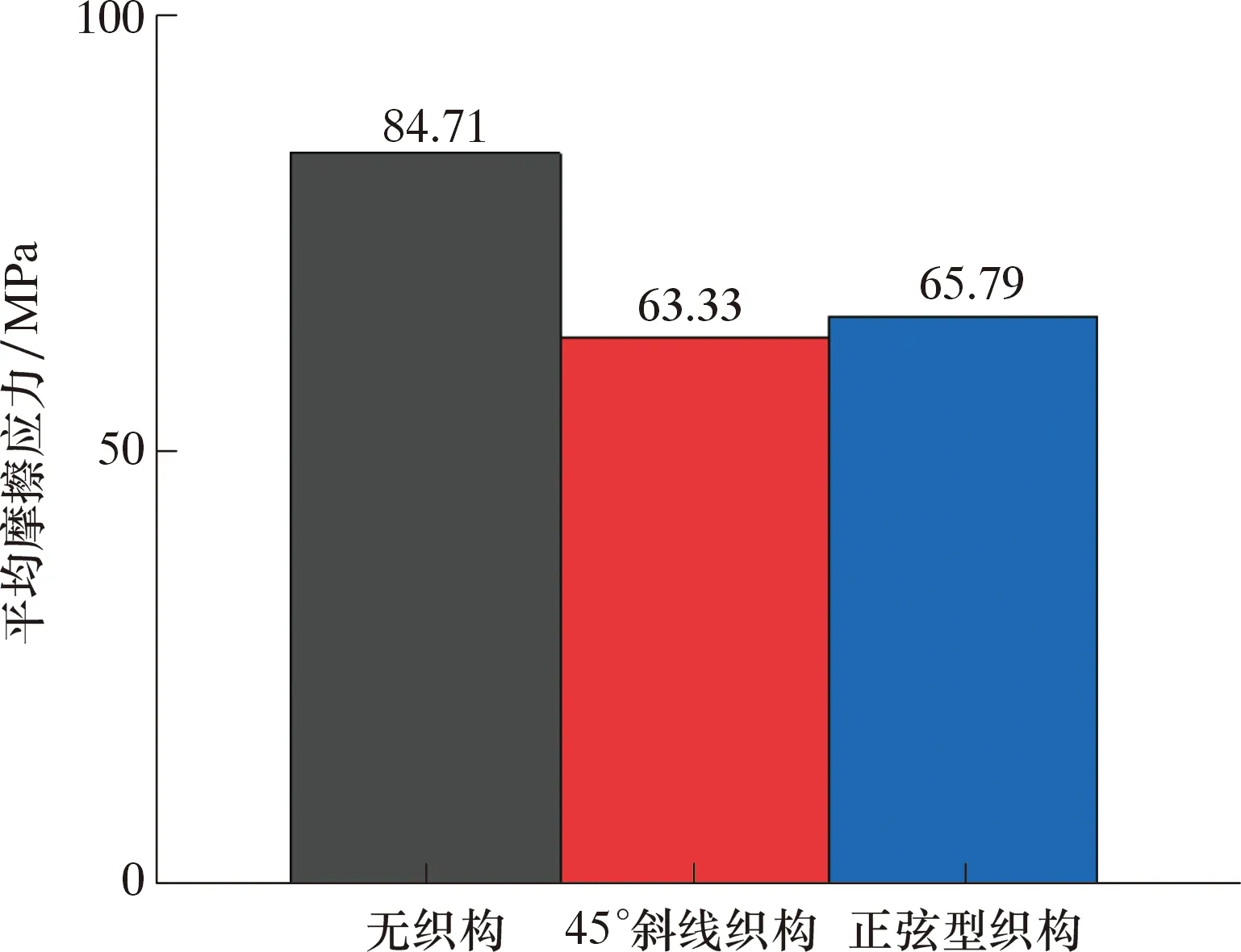
根據對膨脹管的假定,取高為dz的膨脹管圓柱體,則在其任一橫截面內,可視為軸對稱平面應力問題。膨脹管橫截面力學示意圖如圖2所示。由于將膨脹管假設為應力分布均勻,橫截面形狀是圓,呈軸對稱,所以受力也對稱分布。在膨脹過程中,膨脹管單元體的位移、應力是徑向坐標r與軸向坐標Z的函數,與角坐標θ無關[14]。在膨脹錐的作用下,只產生沿半徑r方向的膨脹。由于膨脹管是軸對稱性彈塑性材料,在橫截面上,設半徑a處為彈塑性交界,可知a 圖2 膨脹管橫截面力學示意圖Fig.2 Force diagram of the cross section of the expansion cone 在塑性區域內,各應力分量為: (1) (2) 在彈性區內,由拉梅公式[16],各應力分量為: (3) (4) 由Mises屈服條件可得等效應力滿足: (5) 沿膨脹管壁厚方向任取一圓柱面,設其半徑為r(a≤r≤b),對于平面軸對稱問題,平衡方程為: (6) 由式(5)和式(6)可得: (7) 式中:σr為徑向壓應力,MPa;σθ為軸向拉應力,MPa;σs為屈服極限,MPa。 邊界條件滿足: σ(r=r1)=-p (8) σ(r=r2)=0 (9) 將邊界條件式(8)代入(7),可得: (10) 將式(10)代入式(7)可得: (11) 將式(9)代入式(11)可得: (12) 在膨脹管軸向上,要使某個膨脹管橫截面全部進入塑性狀態,即a=r2,塑性區擴展到外壁,此刻需在膨脹管內壁施加不小于p的壓力,因此p是膨脹錐使膨脹管某個橫截面全部達到塑性狀態所要施加的最小壓力。由牛頓第三定律可知,當膨脹管某個橫截面剛達到塑性變形時,膨脹錐表面受到膨脹管的反作用壓力-p。 定徑膨脹錐主要由3部分組成,如圖3所示。 圖3 膨脹錐微單元受力示意圖Fig.3 Force diagram of an infinitesimal element of the expansion cone 圖3中:L1是導向區,用于引導膨脹錐前進和潤滑液導出;L2是膨脹區,用于擠壓膨脹管;L3是定徑區,用于阻止膨脹管過大的回彈變形,保持最大膨脹半徑[17]。膨脹錐在進入膨脹管后,主要受力為液壓推力、滑動摩擦力、接觸壓力以及自身重力。膨脹錐上微單元受力示意圖如圖3所示,其中忽略了膨脹錐自身重力。在膨脹錐膨脹過程中,由于速度較慢,且波動較小,近似為勻速直線運動,所以受力平衡。 在膨脹錐軸向方向上,由力的平衡關系可得: dF=dfcosα+dNz (13) dNz=dNsinα (14) 滑動摩擦力公式為: df=μdN (15) 由式(13)、式(14)、式(15)可得: (16) df1=μdN1 (17) 式中:dF為該微單元受到的液壓推力,N;dN為膨脹管反作用于微單元的接觸壓力,N;dN1為膨脹管反彈力,N;df為膨脹區微單元受到的滑動摩擦力,N;df1為定徑區微單元受到的滑動摩擦力,N;α為膨脹錐錐角,(°);μ為摩擦因數。 膨脹管對膨脹錐的反作用力主要是垂直于膨脹區表面的dN和垂直于定徑區表面的dN1。dN沿r方向的分力dNr,為膨脹管某個橫截面達到塑性變形所需的最小力;dN沿Z方向的分力dNz,為膨脹管對膨脹錐的阻滯力。dN1為膨脹管介于不完全塑性變形向彈性變形轉變的回彈壓力[18]。膨脹管反作用膨脹錐的壓力為-p,其方向與dNr相同。由壓力的定義可得: dNr=pdS (18) (19) 由式(12)、式(18)和式(19)可得: (20) 式中:R1為膨脹錐小徑,mm;R2為膨脹錐大徑,mm;dS為膨脹區所取微單元面積,mm2;S為膨脹區表面積,mm2。 由三角函數定義: (21) (22) 由式(20)~式(22)可得: (23) (24) 將式(24)代入式(15)可得: (25) 在定徑區,假設膨脹錐受到膨脹管的反作用壓力也是-p。同理可得: dN1=pdS1 (26) S1=2πR2L3 (27) 式中:dS1為定徑區所取微單元面積,mm2;S1為定徑區表面積,mm2。 由式(12)、式(26)和式(27)可得: (28) 同理可得,滑動摩擦力f1為: (29) 采用三維軟件SolidWorks對膨脹錐和膨脹管進行三維立體建模和配合,建模中將膨脹錐小徑和大徑處進行圓角處理,減小應力集中效應。建模參數為:膨脹錐小徑122 mm,錐角12°,L1=50 mm,L2=33 mm,L3=40 mm;膨脹管外徑140 mm,壁厚8 mm,長150 mm,膨脹率12.5 mm。 本文采用有限元方法模擬對比無織構膨脹錐和有2種織構膨脹錐膨脹過程的表面應力分布。現提出2個重要參數:織構走向和面密度。根據當前研究成果,織構走向(形狀)和面密度對試件的減摩抗磨性能有著重要影響。張貴梁等[19]利用激光技術在硬質合金表面制備了一種正弦狀溝槽型微織構,并進行摩擦磨損試驗;試驗結果表明,在同樣的試驗條件下,正弦型微溝槽織構試樣比傳統直線型微溝槽試樣具有更好的減磨效果。因此本文設計織構形狀為三角形微溝槽,包括45°斜線走向和正弦型走向。45°斜線走向微溝槽織構沿膨脹區圓臺外表面方向均勻布置;正弦型走向微溝槽織構沿膨脹區圓臺母線方向均勻布置。圖4為2類織構布置示意圖。 圖4 2類織構布置示意圖Fig.4 Schematic diagram of two texture configurations 圓臺側面展開是扇形,定義織構在扇形面上布置的條數與扇形面積的比值為表面織構分布率η,即: (30) Sc=πL(R3+R4) (31) 式中:n為織構條數,取30;L為圓臺母線長,為33.7 mm;R3為圓臺上底半徑,為61 mm;R4為圓臺下底半徑,取67 mm;Sc為圓臺側面積。代入數據得Sc=1.354 4×104mm2,η=2.2×10-3條/mm2。 取45°斜線和正弦型微溝槽織構表面分布率相同,便于對比2種不同走向織構的摩擦性能。單條微溝槽織構的尺寸由其槽寬w和深度d確定,長度由母線L決定。因2類織構的截面都呈三角形,所以取其槽寬w和槽深d分別相同。微溝槽織構結構示意如圖5b所示,建模中取w為0.1 mm,d為0.3 mm,在SolidWorks中采用掃描切除和陣列命令進行織構創建,創建織構后的膨脹錐三維模型如圖5a、圖5c所示。 圖5 織構結構和模型建立Fig.5 Textures and modeling 本文利用ANSYS Workbench進行有限元仿真模擬,選擇靜力分析解法求解,膨脹錐選用硬質合金,膨脹管選用不銹鋼。2種材料主要力學性能參數如表1所示。 表1 材料主要性能參數Table 1 Main material performance parameters 分析過程中有如下簡化假設:①膨脹錐的運動屬于緩慢勻速直線運動,即視為受力平衡;②摩擦因數恒定;③膨脹錐硬度遠大于膨脹管,不考慮其變形;④因膨脹速度緩慢,所以忽略摩擦生熱和振動;⑤在計算過程中無潤滑條件,視膨脹錐與膨脹管之間為干摩擦[20];⑥膨脹管為理想彈塑性材料,材料經過線彈性階段后進入流動階段,最后進入塑性階段。 該過程是剛體-柔體接觸問題,涉及材料、幾何、狀態非線性一體的非線性大變形分析。設定摩擦接觸類型為罰函數法,摩擦因數為0.15。因膨脹錐硬度遠大于膨脹管,選定膨脹錐膨脹區和定徑區外表面為目標面,膨脹管內壁為接觸面,接觸方式為面-面接觸。因要查看膨脹錐表面應力,目標面和接觸面均設為彈性體。接觸對設置如圖6a和圖6b所示。 圖6 模型前處理Fig.6 Pre-treatment of the model 對于該模型的分析,主要關注2種織構對膨脹錐接觸表面應力分布的影響。在模擬過程中,計算結果的精度和收斂性取決于建模的合理性和網格劃分的質量。由于織構的尺寸相對于模型來說非常小,所以在網格劃分的過程中需要進行局部細化。這樣不僅可以提高計算結果的精度,同時也避免了模型統一采用較小的網格尺寸導致劃分的單元數過多,從而計算時間太長或不收斂問題。本文利用ANSYS Workbench Mesh軟件進行網格劃分。由于膨脹錐織構化部位在膨脹區,且織構尺寸較小,不便于采用六面體單元劃分,故膨脹區采用四面體單元,其他部分采用自由劃分;網格尺寸設為1 mm,網格物理選項設為非線性結構。劃分網格后的模型如圖6c所示。 在ANSYS Workbench中,載荷和約束是有限元模型求解的邊界條件。對膨脹管的下端圓環面施加Y方向0位移約束,對膨脹錐設置Y向位移,沿Y軸正方向移動100 mm,移動期間無旋轉和平移。邊界條件設置如圖6d所示。 為了降低模型計算量,調整接觸法向剛度因子為0.1,設置初始接觸與滲透條件以及載荷子步選項控制,打開大變形,最后進行求解。計算完成后,以膨脹錐接觸面為查看對象,得到最終狀態下的總變形、等效應力(von Mises)云圖。 首先進行無織構膨脹錐的膨脹過程模擬,旨在分析膨脹過程中膨脹錐變形和接觸應力的分布情況,結果如圖7所示。 圖7 無織構膨脹錐的變形與應力Fig.7 Deformation and stress of the expansion cone with no textures 由圖7a可知,膨脹錐在沿Y軸正方向移動100 mm后,膨脹錐接觸外表面出現了較大的變形。膨脹錐最大變形區域在定徑區最下端,而在膨脹區,小徑處變形量也較大。原因是定徑區尾部受到膨脹管的回彈擠壓和外部推力作用,而小徑處最先與膨脹管接觸,受到膨脹管阻滯作用。由圖7b可見,膨脹錐最大等效應力主要集中在大徑處的圓周區域,在圓周區域一周內存在多個最大應力集中點,最大應力為771.60 MPa,且最大應力在圓角區上端處。這是因為在膨脹過程中,該區域是最大膨脹半徑,受到接觸力、摩擦力以及膨脹管流動和阻滯等多重作用,使得該區域的應力較大,出現了應力集中的現象。而膨脹錐的其他區域,尤其是定徑區,是大變形區,但表面應力較小,膨脹過程對該區域應力影響較小。因此,后文主要從織構所處的膨脹區進行應力分析。 研究發現,通過在材料表面制備出合理的紋理,能更好地改善接觸狀態,增強材料的抗磨性。表面微織構化處理是常見的方式之一,常規的微織構幾何形狀有圓形凹坑、三角形凹坑、直線和網格凹槽等[21]。本文在膨脹錐膨脹區設置如圖4所示的2種走向三角形微溝槽織構,保持膨脹條件一致,進行膨脹模擬。圖8為45°斜線走向織構化膨脹錐膨脹100 mm后的應力分布云圖。 圖8 45°斜線走向織構化膨脹錐應力分布Fig.8 Stress distribution of the expansion cone with 45° inclined microgroove textures 由圖8可知,最大應力出現在膨脹錐大徑上端處,分布區域極小并且只有幾處是最大應力集中點。一方面該處是最大膨脹半徑,擠壓程度最強;另一方面,由于膨脹區表面建立了斜線微溝槽織構,使表面出現了不連續變化,易在織構周圍區域出現小范圍的應力集中;同時該處是織構結束點,存在尖銳的邊界,尖銳的邊緣往往存在應力集中尖峰,因此在該處最大應力達到967.11 MPa,接近無織構膨脹錐的1.25倍。 在條數相同情況下,相對于45°斜線走向織構,正弦型走向織構的面積分布率大于45°斜線走向織構,增加了表面粗糙度,減少了摩擦副的直接接觸面積,同時存在更多個不連續變化區域,將導致應力集中更明顯[22]。圖9為正弦型走向織構化膨脹錐膨脹后的應力分布圖。由圖9可知,在膨脹100 mm后,帶正弦型織構膨脹錐表面的最大應力集中在正弦曲線的拐角處,整個膨脹區表面只有一處為最大應力集中點,達到1 107 MPa,大約是45°斜線走向織構的1.14倍。在該處產生應力極大,原因是該處是不連續變化區域,織構走向出現變向,從而引起較大的應力集中。 圖9 正弦型走向織構化膨脹錐應力分布Fig.9 Stress distribution of the expansion cone with sinusoidal microgroove textures 織構化摩擦副在摩擦過程中,織構的存在可以收集和排出磨屑,以及存儲潤滑油、潤滑脂,并且有效阻止二次磨粒磨損、減輕摩擦波動。研究表明,將激光織構化后的鈦合金試樣進行干摩擦試驗,試驗表明,無論是直線織構、網格織構還是凹坑織構,都起到了減少磨損、增強耐磨性的作用[23-24]。織構化試樣的摩擦機理為:干摩擦條件下,通過凹坑或凹槽捕獲磨屑,減小磨粒磨損效應;潤滑狀態下,能儲存潤滑油,拓展摩擦副上油膜流體動壓潤滑的發生范圍;在貧油狀態下,微織構儲存的潤滑油,在摩擦運行過程中通過對偶的擠壓能溢到摩擦副表面,從而形成臨時油膜,避免過早進入干摩擦狀態[25-26]。 下面在ANSYS軟件中通過接觸工具查看無織構和帶不同織構膨脹錐膨脹過程中最大摩擦應力隨時間變化趨勢,從摩擦應力的角度分析表面織構化膨脹錐干摩擦性能的影響機理。圖10是無織構膨脹錐和織構化膨脹錐膨脹過程中最大摩擦應力隨時間變化曲線。由圖10可知,在膨脹模擬過程中,摩擦應力變化趨勢是先增大再減小最后趨向于相對穩定。原因是在建模時,設置了膨脹錐與膨脹管有一定的過盈量,剛開始時摩擦應力不為0;隨著膨脹進行,擠壓程度變強,摩擦應力變大。當膨脹錐繼續往前推進,逐漸進入膨脹管,其與膨脹管接觸狀態趨于穩定,因此到后期摩擦應力趨于相對平穩。無織構膨脹錐膨脹穩定后,其最大摩擦應力均大于帶織構膨脹錐,因此在膨脹錐表面加工一定形狀的織構可以減小摩擦應力,因為摩擦表面上存在溝槽可以減小接觸面積,同時存儲磨屑。由圖10還可得出,無織構膨脹錐在膨脹穩定后,其最大摩擦應力波動程度小于帶織構膨脹錐,且正弦型織構膨脹錐波動幅度最大,其原因是帶織構的膨脹錐表面粗糙度較無織構膨脹錐大。因此在干摩擦條件下無潤滑油填充易出現波動,同時在相同織構條數前提下,因正弦型織構比斜線織構分布面積更大,所以正弦型織構膨脹區的表面粗糙度也更大,導致膨脹過程中出現較大的波動性。 圖10 膨脹錐最大摩擦應力隨時間變化曲線Fig.10 Maximum friction stress of the expansion cone vs.time 平均摩擦應力可以反映膨脹錐在膨脹過程中的摩擦性能。設定摩擦因數恒定為0.15,得到3種膨脹錐的平均摩擦應力柱狀圖,如圖11所示。由圖11可知,無織構膨脹錐摩擦應力大于有織構膨脹錐,且45°斜線織構膨脹錐的平均摩擦應力最小。因此,在膨脹錐表面加工斜線織構能減小膨脹錐摩擦應力,起到減摩作用。同時,由于織構溝槽具有存儲磨屑、減小摩擦應力和摩擦表面間接觸面積等優點,能夠有效減輕膨脹錐的表面磨損。 圖11 膨脹錐平均摩擦應力Fig.11 Average friction stress of the expansion cone (1)無織構膨脹錐的最大等效應力集中在大徑圓角上端處,集中點較多,因該處是最大膨脹半徑,擠壓程度最強烈,最大等效應力為771.6 MPa。 (2)相對于無織構膨脹錐,帶織構膨脹錐因表面出現了不連續變化,在織構處的局部區域出現更大的應力,但集中點較少。在相同條數下因正弦型織構的面積分布率大于45°斜線織構,使表面粗糙度更大,因此最大等效應力約是45°斜線走向織構膨脹錐的1.14倍。 (3)無織構膨脹錐膨脹過程中最大摩擦應力和平均摩擦應力均大于帶織構膨脹錐,但因帶織構膨脹錐的表面粗糙度大于無織構膨脹錐,所以膨脹穩定后波動性較大,但在潤滑狀態下可緩解波動。 (4)織構溝槽具有存儲磨屑、減小摩擦應力、減少摩擦表面間接觸面積等優點。就本文研究來看,在膨脹錐表面加工溝槽織構可以減小膨脹錐摩擦應力,其中45°斜線走向織構減摩效果最好。因此將織構應用到膨脹錐表面可以達到減摩作用,能有效降低膨脹錐的表面摩擦應力,延長使用壽命。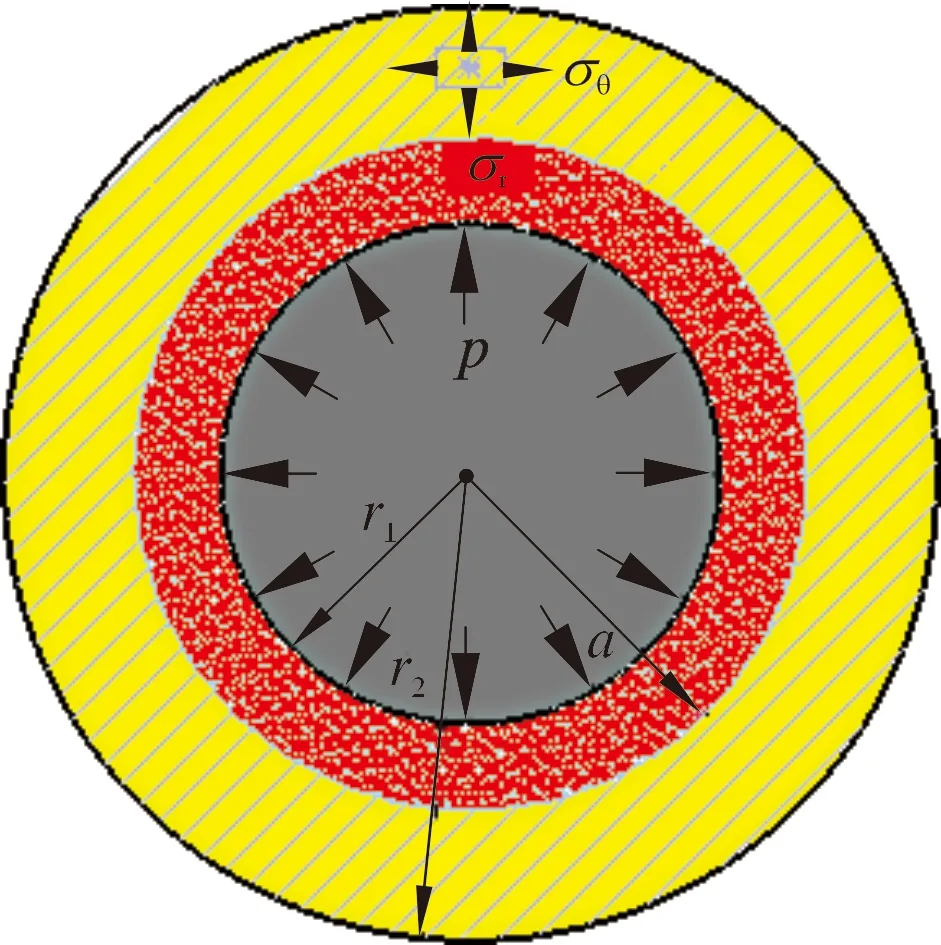
1.2 膨脹錐受力計算
2 有限元分析
2.1 模型建立
2.2 材料屬性和接觸設置
2.3 網格劃分
2.4 邊界條件
2.5 計算結果與分析
3 微溝槽織構對應力的影響
3.1 對等效應力的影響

3.2 對摩擦性能的影響
4 結 論

