基于文丘里管濕天然氣計量虛高系數數值模擬研究*

魏方方 董建宏 張倩 矯欣雨 檀朝東 吳浩達

(1.安徽中控儀表有限公司 2.中聯煤層氣有限責任公司 3.中國石油大學(北京)石油工程學院 4.中石化勝利油田魯明公司)

0 引 言

濕天然氣流量的在線測量既可以降低氣田投資和運營成本，也為簡化生產工藝、提高氣藏綜合管理水平提供科學依據。從氣井采出的天然氣普遍含液相，而經過分離后的干天然氣經過長途運輸及溫度壓力改變后也可能析出液體，變成濕天然氣[1-2]。濕天然氣的計量一直是油井產量計量研究中的難點問題[3]。文丘里管作為常用的濕天然氣計量流量計，擁有結構簡單造價低廉等特性，國內外很多商用濕氣和多相流量計都采用它進行[4]。通常差壓式流量計只適用于牛頓流體的測量，其流體在組成和熱力學上是均勻單相，符合牛頓內摩擦定律。當被測流體夾帶少量的其他相介質通過差壓式流量計時，壓差值就會發生顯著變化。寇杰等[5]通過試驗對比證明了文丘里管流量計比孔板流量計計量更加精確，進行濕天然氣計量時，附加的壓力損失大小取決于若干參數，如壓力、溫度、流型等。當文丘里管流量計用于濕天然氣計量時，濕天然氣產生的壓差通常比氣體中沒有液體時大，通常會導致差壓流量計的氣體流量出現正誤差，即“虛高”現象。當前國內外學者也提出各種虛高模型，這些模型都是針對工業濕氣測量而提出來的，這些流量計的入口直徑都在50.8～1 219.2 mm(2～48 in)范圍[6]。C.BRITTON等[7]在研究文丘里管測量濕天然氣時發現，在濕天然氣參數不變，流經入口直徑不同、其他參數相同的2個文丘里管時，入口直徑越小虛高越小。2012年，HE D.H.等[8]對濕天然氣在文丘里管的流動進行數值模擬研究，將不同的湍流模型進行對比，結果表明，標準k-ε模型優于其余湍流模型，在迭代計算中能夠較快收斂。2013年，K.PERUMAL等[9]對不同尺寸的文丘里管進行濕天然氣流動數值模擬研究，并分析文丘里管的幾何尺寸對濕天然氣虛高的影響，結果表明：文丘里管入口直徑越大，節流比對流出系數影響越小，收縮角越大流出系數越小，節流比越大虛高值越小。P.KUMAR等[10]利用Fluent軟件對濕天然氣在文丘里管內的流動進行了數值模擬，文丘里管的節流比為0.4保持不變，設置了不同的收縮角與擴張角，并進行組合。

以上關于濕天然氣計量虛高的研究，更多的關注是節流器本身結構對濕天然氣(大多數研究介質為蒸汽、氣水混合物)虛高的影響，很少針對濕天然氣計量和實際應用工況開展虛高研究。為此，筆者根據現場計量裝置建立了文丘里管的物理模型，用Fluent軟件進行濕天然氣流體仿真模擬(CFD)研究，仿真模擬單氣相、單液相、氣液兩相在文丘里管內流動特性，提出文丘里管內濕天然氣虛高測量的數值模擬方法，并對虛高系數模型進行評價。

1 濕天然氣計量物理模型

當流體從文丘里管的上游流入收縮段時，由于流通面積的減小，流體將在收縮段內局部收縮。由連續性方程可知，流體速度增大，靜壓降低。因此，在收縮段前后會產生一定的壓差，流體流量越大，壓差就越大，從而可以通過測量收縮段前后的壓差值來測量流體流量。文丘里管結構如圖1所示。第1與第2壓差取壓測點的壓差為Δp1，第2與第3壓差取壓測點的壓差為Δp2，第1與第3壓差取壓測點的壓差為Δp3。當文丘里管內為混相流動時，Δp1記為Δptp。這種流量測量的方法以流體連續性方程和伯努利方程為基礎推導出。對于尺寸規格一定的文丘里管，當上下游取壓口位置、出入口直管段以及流體參數已知時，就可以通過測量上游與喉道之間產生的壓差來計算流體的流量。

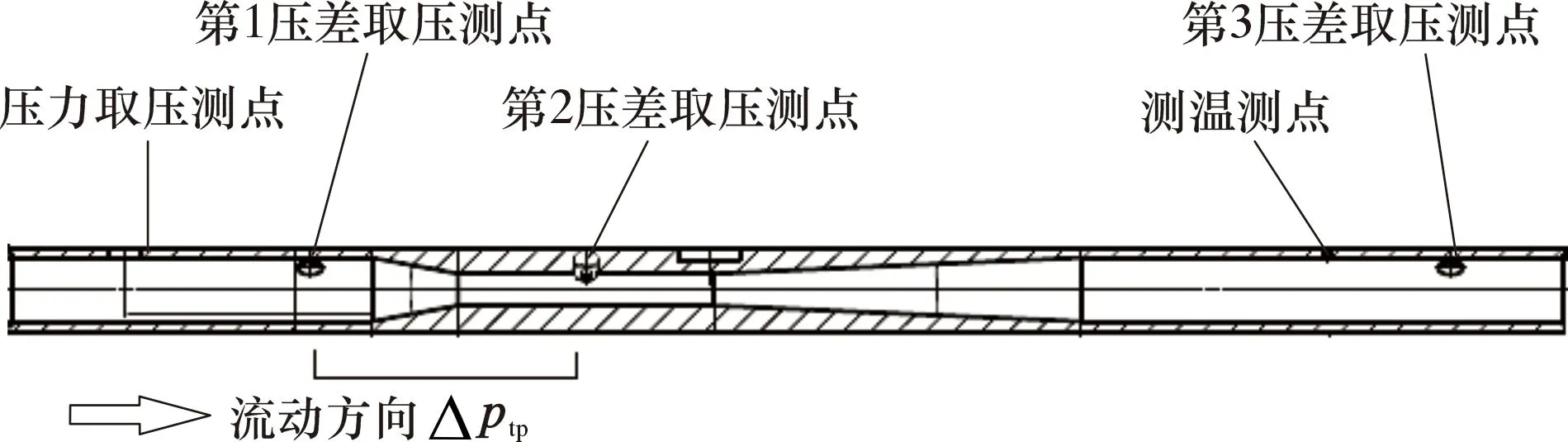
圖1 文丘里管結構圖Fig.1 Structure of the Venturi tube

由于流體流動會產生局部損失與摩阻壓降，計算中引入流出系數C修正計量公式；氣體為可壓縮流體，流經節流處氣體會被壓縮，因此引入可膨脹性系數ε進行修正。

根據伯努利原理及連續性方程可得到質量流量壓降關系式，單相氣體計量的基本公式為：

(1)

式中：Wg為氣相質量流量，kg/s；d為喉部直徑，m；β為節流比(喉道內徑與上游測量管內徑比)；Δp為節流差壓，Pa；ρg為密度，工況節流上游流體密度，kg/m3。

文丘里管內濕天然氣的測量就是要研究濕天然氣中由于液相的存在對氣相壓差Δp的影響，并比較精確地計算出變化量的大小。當濕天然氣流過壓差式流量計時，由于氣相夾帶少量的液相，通過壓差式流量計時產生的壓差值會比等量的氣相單獨流過時偏高，這種壓差值升高的現象稱為“虛高”，虛高系數NOR計算式為：

(2)

式中：Δpg為等量的氣相單獨通過同一文丘里管時的壓差，Pa。

將虛高的壓差值帶入式(1)即可得到虛高的氣質量流量：

(3)

式中:Wg′為氣體的虛高質量流量，kg/s。

實際的氣相質量流量值即為式(3)與式(2)之比，即：

(4)

2 基于CFD模擬的虛高改進模型研究

對于濕天然氣，由于其連續相為可壓縮氣相且測量對象為氣液兩相流，測量壓差與液相含量、壓力等相關。所以采用壓差式流量計對濕天然氣中的氣相進行測量時，還需要考慮由于液相存在對氣相測量的影響，并引入相關的修正系數進行修正。利用Fluent軟件對文丘里管內的濕天然氣在不同壓力、不同氣相體積流量和不同液相體積分數下進行迭代計算。求解得到不同流量與含氣體積分數下的壓力場與速度場。參照現場工況設置模擬試驗參數，仿真模擬不同工況下濕天然氣計量的虛高系數NOR。

2.1 濕氣流量虛高計算解析模型

當前各研究者建立了很多壓差式流量計測量濕氣的虛高計算解析模型，這些模型都以均相流和分相流理論[11-19]為基礎，如表1所示。

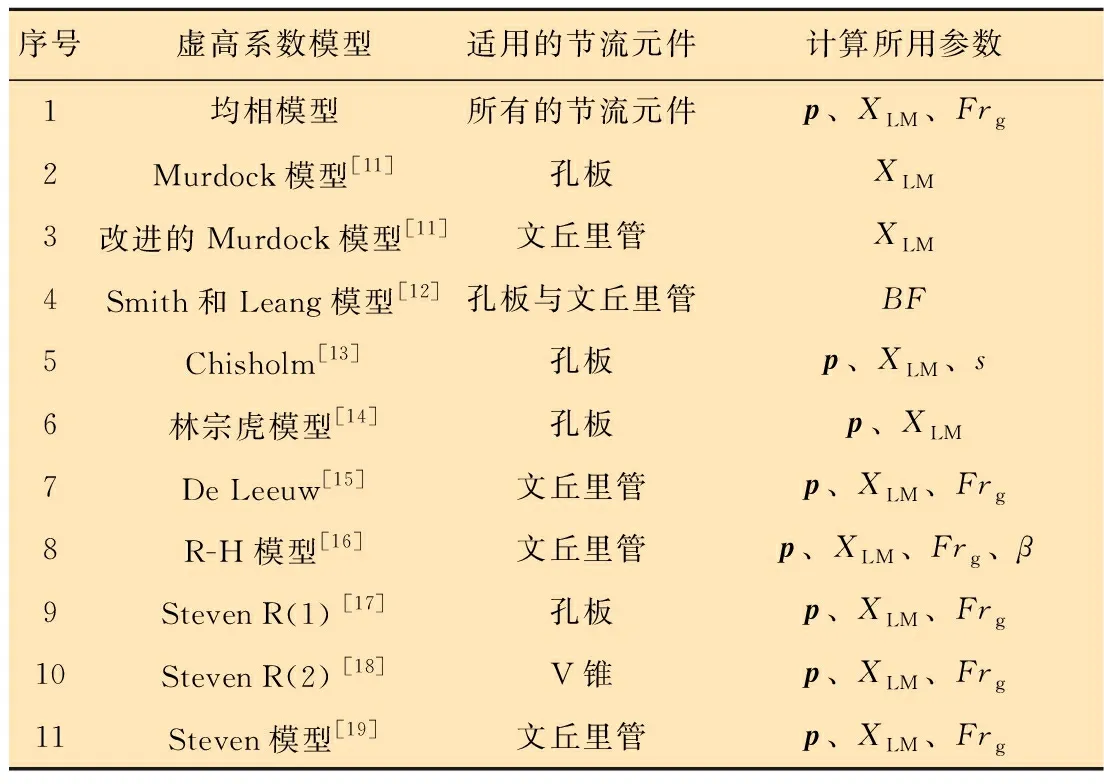
表1 濕氣流量虛高計算模型Table 1 Summary of calculation models predicting flow rate over reading for wet gas

由以上虛高修正系數計算模型可知，Lockhart-Martinelli參數XLM、氣相Froude常數Frg為表現濕天然氣中液相和氣相影響的重要參數。

Lockhart和Martinelli把混相中等量的液相、氣相單獨流過節流件時，壓差比值的平方根定義為Lockhart-Martinelli參數(簡稱LM參數)。

(5)

式中：Δpl、Δpg分別為等量的液相、氣相單獨流過節流件時的壓差，Pa；ρg、ρl分別為氣相和液相的密度，kg/m3；Wl和Wg分別為液相和氣相的真實質量流量，kg/s。

W.Froude為表示重力對流動影響的準數，提出了氣相Froude常數Frg，可以表示為：

(6)

式中：vsg為氣相表觀速度，m/s；g為重力加速度，m/s2；D為入口直徑，m。

2.2 虛高模型的CFD模擬研究

參照現場工況設置模擬試驗參數，(CFD)仿真模擬不同工況下濕天然氣通過文丘里管時的壓差Δptp和等量的單相天然氣單獨通過同一管時的壓差Δpg，根據公式(2)計算虛高系數NOR，并對兩相流與單相流的壓降影響因素開展討論。

2.3 模型建立與網格生成

CFD模擬中，利用DesignModel將圖1所示的物理模型建立3D 水平文丘里管幾何模型(見圖2)，進行網格劃分和網格獨立性研究。網格生成過程主要選擇三角形和四邊形，生成網格如圖3所示。

圖2 文丘里管幾何模型Fig.2 Geometric model of the Venturi tube

圖3 網格建立圖Fig.3 Grid division of the model

2.4 前處理設置

利用Fluent進行求解時，選擇優于其余湍流模型的k-ε的模型計算文丘里管節流裝置內的氣液兩相流動，流體模型選擇適用于多相流的VOF模型。壓力和速度的耦合采用多相流模型中適用于穩態流動的Simple模型。進口采用速度入口邊界條件；出口采用壓力出口邊界條件；壓力方程的離散采用標準格式；動量方程的離散采用一階迎風格式。在迭代計算過程中，設置殘差精度為10-4。

2.5 Fluent模擬結果分析

對Fluent模擬結果進行分析，主要為：總結節流元件內部壓力場與速度場的變化規律；對比單氣相流動與加入了液相成為濕氣兩相流的流動之間的不同以及變化規律；不同的液相含量對壓降的影響。

(1)單氣相的管內流動仿真。為簡單了解流體在節流管件內的流動，根據其流場特性對軟件中設置的條件進行了調整，邊界條件設置為速度入口與壓力出口，并對文丘里節流元件進行了單相氣流動模擬。圖4 和圖5給出了文丘里管內和管軸心處的壓力分布。文丘里管內部流速分布如圖6所示。

由圖4可知，上游直管段有較小的壓力降，說明流體流動造成了壓力損失，數值遠小于局部節流造成的壓力損失，但也可能給計量結果帶來誤差。由圖5可知，在同一橫截面的流體靜壓也不盡相同，在入口附近等壓線為弧形，由靠近管壁處的流體與管壁之間的摩阻所造成，因此流體流動過程中管壁處與軸心處的壓力不同。當流體進入收縮管段，壓力驟降，且靠近喉道處的壓力下降較快。喉部直管段直徑不變但壓力逐漸降低，說明在喉道處流體流速依然增加且存在壓力損失。喉道與擴張管段交接處壓力達到最低，進入擴張段后壓力逐漸恢復。由圖6可知，上游直管段流速緩慢增加，收縮段流速增加迅速，節流管段流速仍沿流動方向緩慢提升，擴張段與下游直管段流速逐漸降低。

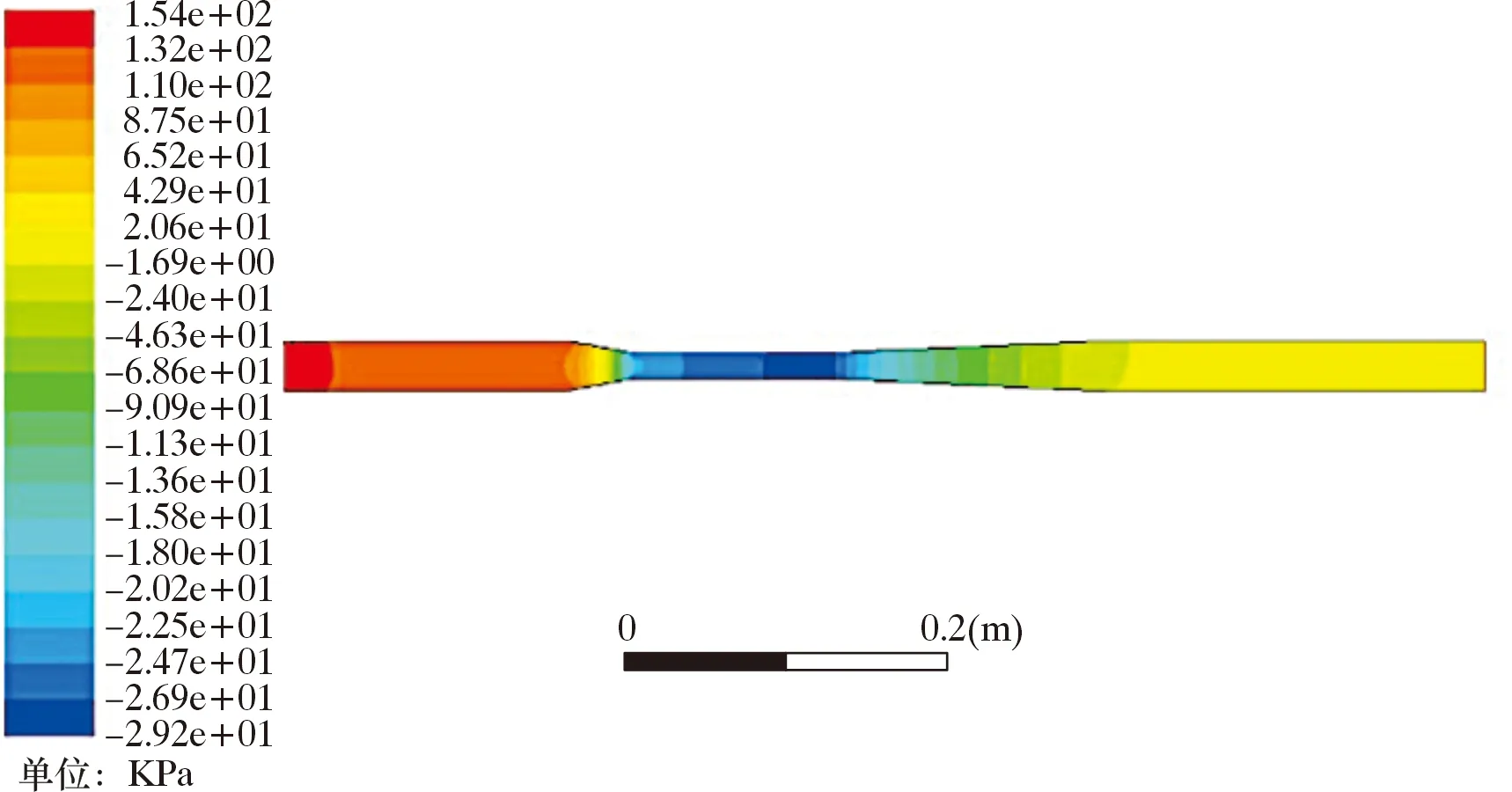
圖4 文丘里管壓力場分布圖Fig.4 Pressure distribution through the Venturi tube

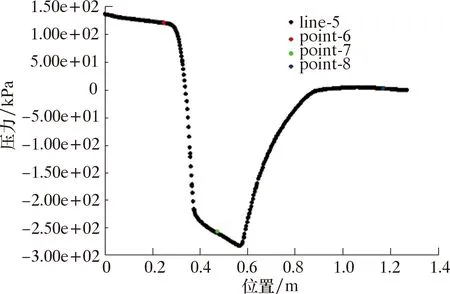
圖5 文丘里管軸心處壓力分布Fig.5 Pressure distribution along the Venturi tube axis

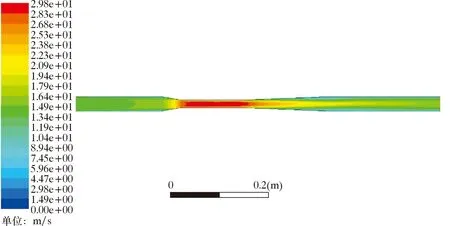
圖6 文丘里節流件內部速度場分布圖Fig.6 Velocity distribution inside the Venturi throttle

(2)兩相流與單相流的壓降仿真結果對比。模擬了單氣相、單液相、氣液兩相流經文丘里計量裝置的流動壓降。圖7給出了流量100 m3/h的單氣相、1 m3/h的單液相、等量氣液混相文丘里管的流動壓力對比。橫坐標表示文丘里管沿著X軸方向的位移變化，其中起點為文丘里管的入口端面。由圖7可知，氣液兩相進入收縮段后產生的壓降遠大于單相流經喉道產生的的壓降，且壓力恢復最慢。該現象產生的原因除了喉道處流體流通面積減小，流速上升導致壓力降低以外，還包括了氣液兩相流動時相之間的摩阻。氣液兩相流動中氣相的流速大于液相流速，對液相有攜帶作用。

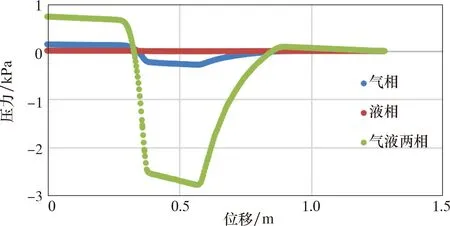
圖7 文丘里管的單相與兩相流動壓力對比Fig.7 Flow pressure comparison: single-phase vs.two-phase

(3)液相含量對壓降的影響。仿真模擬了液相流量分別為1、2、3、4 m3/h(998、1 996、2 994、3 992 kg/h)、氣流量固定為100 m3/h(122.5 kg/h)的氣液兩相流過文丘里管的壓力和速度，結果如圖8和圖9所示。由圖8可知，液相流量越高，流體進入收縮段的壓力降低越明顯，產生的壓降越大。由圖9可知，液相體積含量在較低數值上變化時，文丘里管內部的流體流速變化不大，因此，壓降的變化受流體速度影響不大。液相作為離散相彌散在流場中的數量越多，對氣相流動的阻礙越大，氣相攜帶液相造成的壓力損失越大。液相流動產生的局部損失同樣是壓力降低的原因。因此，為了準確計量濕氣的氣相流量，需要對不同含液體積分數的濕氣進行準確的虛高修正計算。

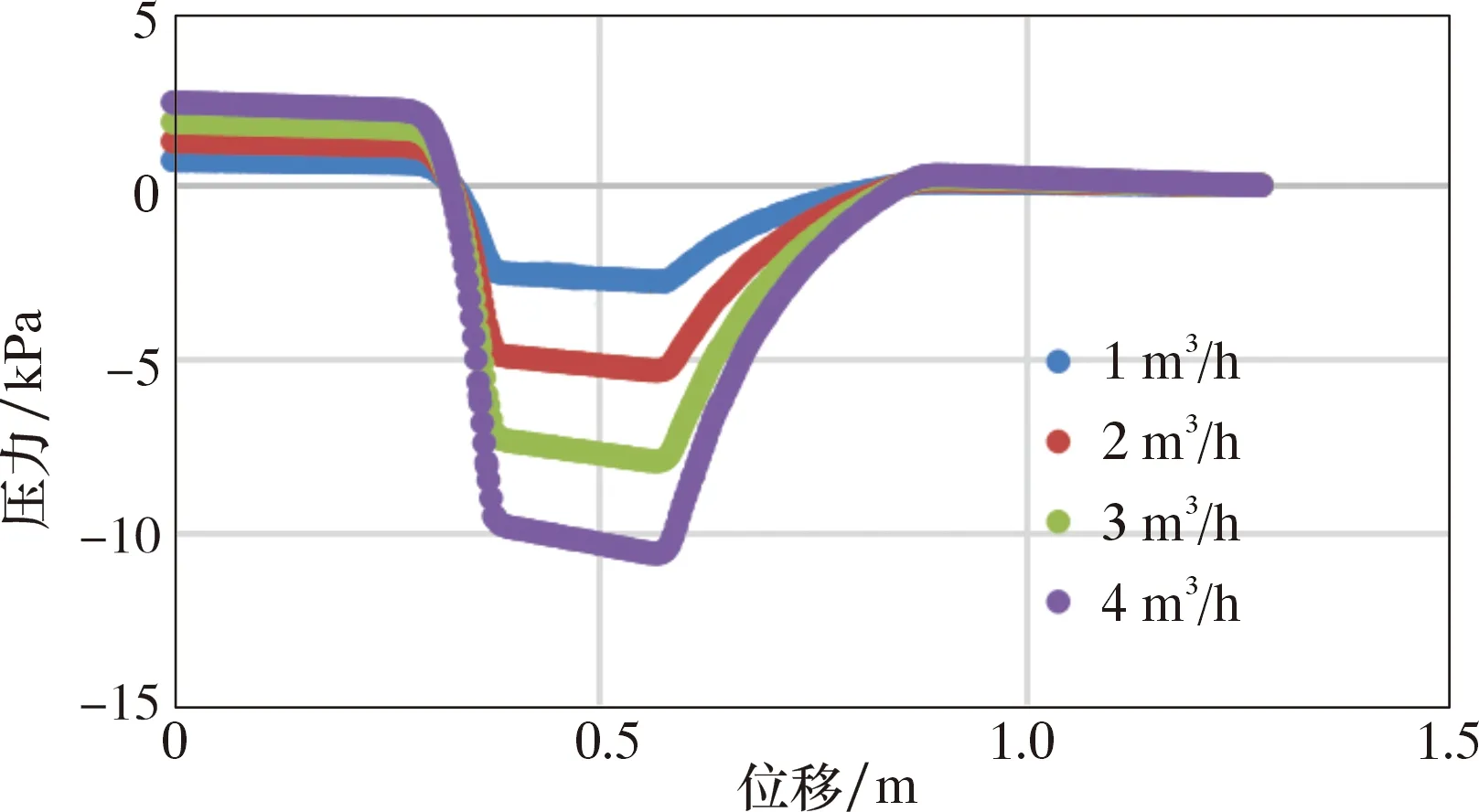
圖8 文丘里管不同液相流量的壓力對比Fig.8 Pressure comparison of the Venturi tube for different liquid flow rates

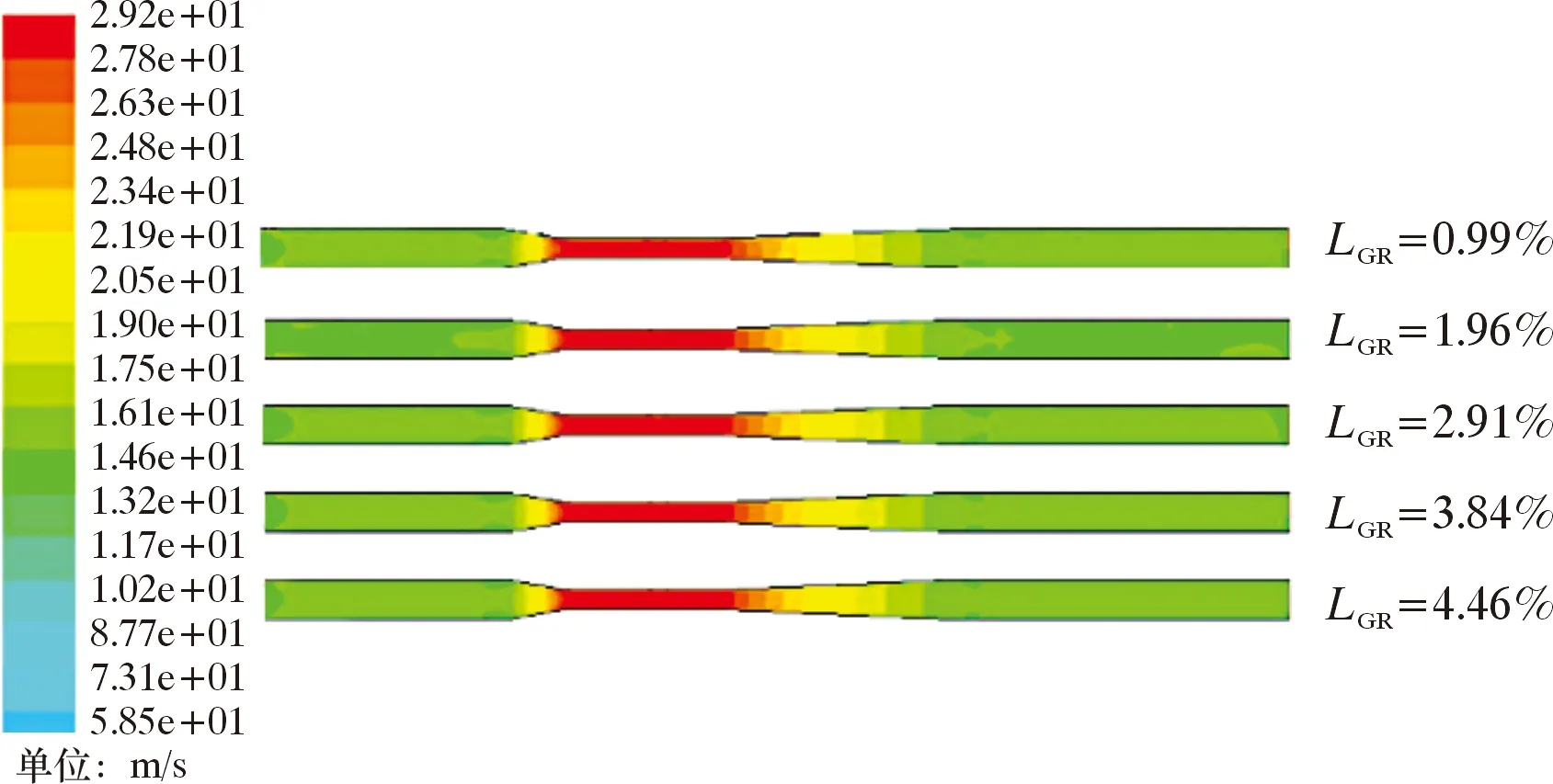
圖9 文丘里管不同液相含率的速度云圖Fig.9 Velocity contour map of the Venturi tube for different liquid holdups

(4)氣相含量對壓降的影響。仿真模擬了液相流量固定為1 m3/h(998 kg/h)，氣相流量分別為50、70、100 m3/h(61.25、85.75、122.5 kg/h)的氣液兩相流經文丘里管的壓力，如圖10所示。

由圖10可知，液量固定時，氣量越大，節流處產生的壓降越大。主要原因是：氣量越大，流體流速在節流處加快越明顯，根據能量守恒，壓力降低也越明顯。

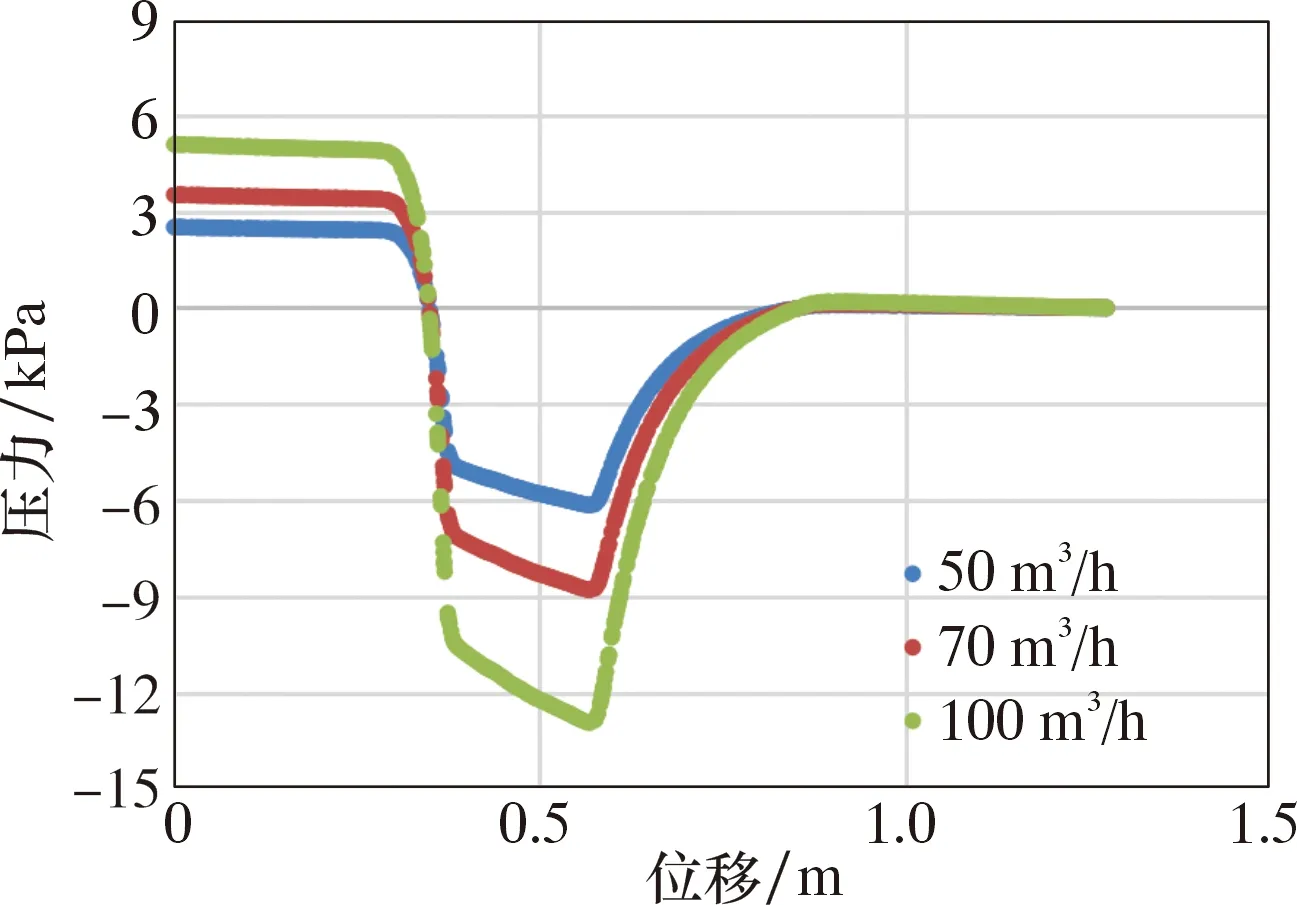
圖10 文丘里管不同氣相流量的壓力對比Fig.10 Pressure comparison of the Venturi tube for different gas flow rates

3 虛高模擬計算結果對比分析

3.1 虛高系數NOR的影響因素分析

本文進行了不同工況和模型下的多組模擬試驗，得到濕天然氣虛高修正系數NOR與XLM、Frg、ρg/ρl的關系圖。

(1)LM參數XLM。圖11為NOR與XLM的關系圖。由圖11可知，虛高修正系數NOR隨XLM的增大而增大，兩參數成正相關。但隨著XLM增大，圖11中的函數點逐漸發散，說明虛高修正系數不完全是XLM的函數。

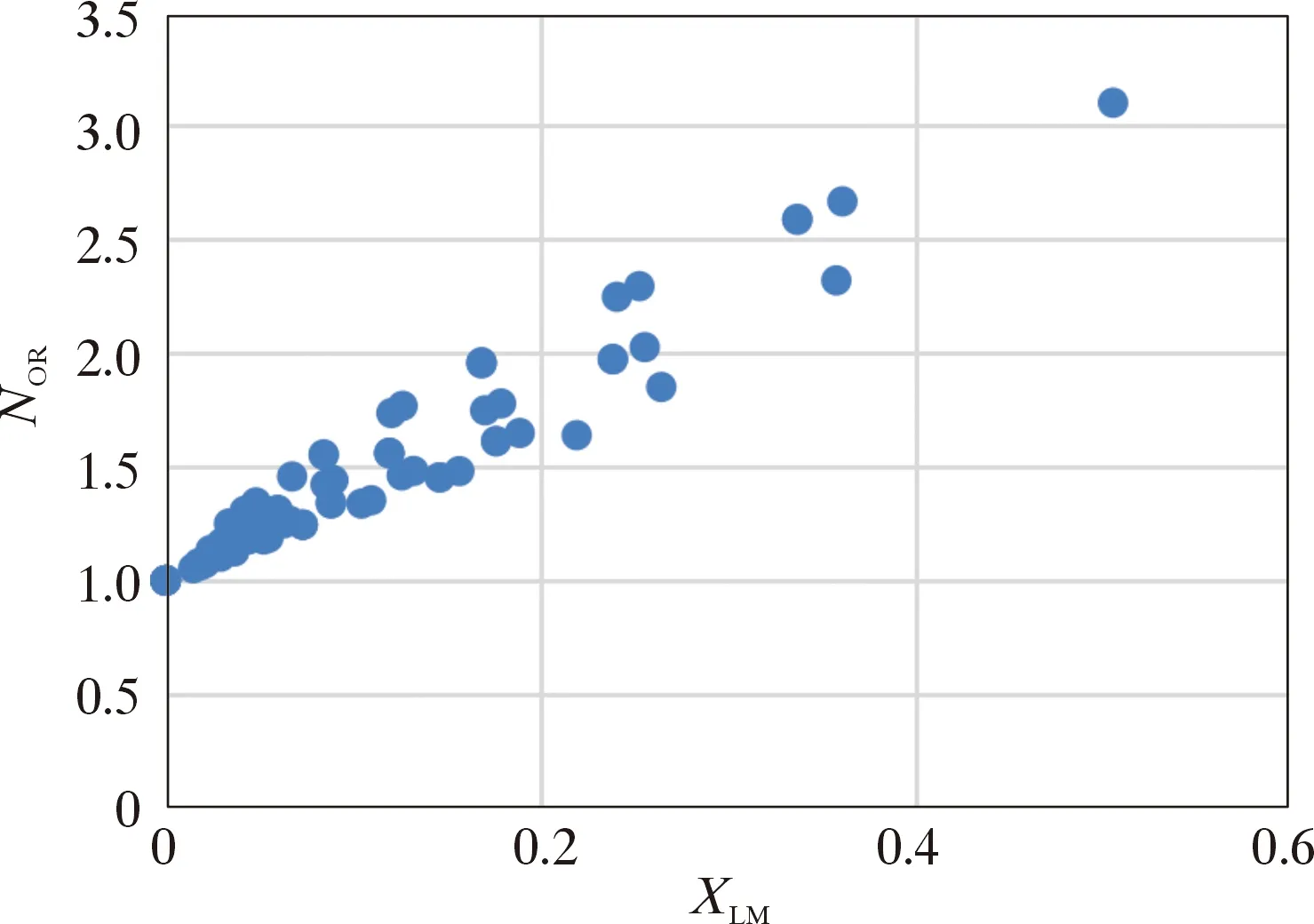
圖11 NOR與XLM關系圖Fig.11 Over reading correction coefficient NORvs.Lockhart-Martinelli factor XLM

(2)氣相Froude常數Frg。圖12是文丘里管不同壓力下NOR與Frg、XLM的關系。在相同壓力下不同Frg與NOR增加趨勢相同；隨著壓力的增加，同體積流量下的XLM參數減小，虛高也同時變小。

Frg是氣相表觀速度與氣相、液相密度的函數，當壓力確定時，流體密度即為常數值。圖12表明在相同的壓力條件下，NOR僅與XLM有關。

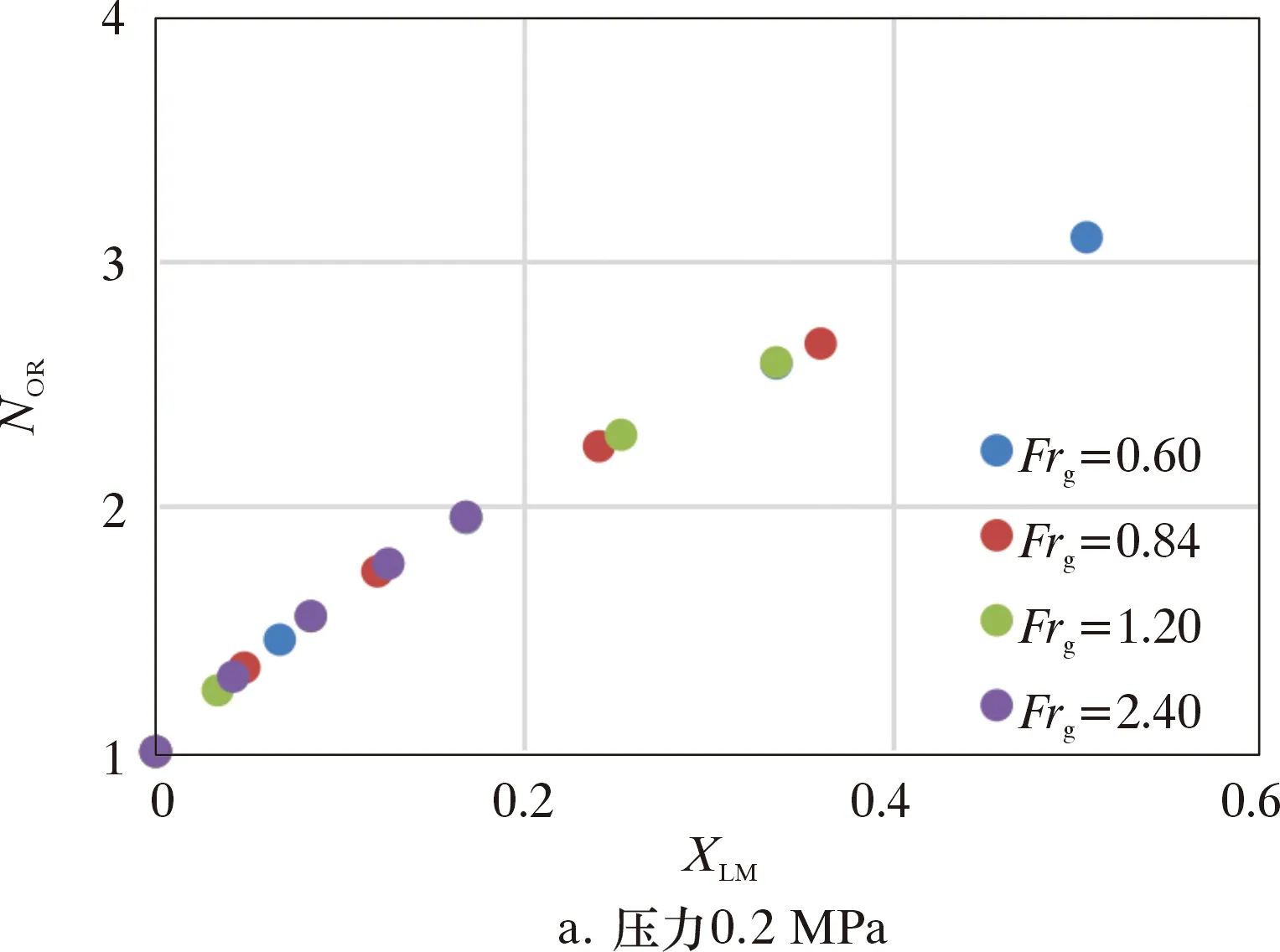
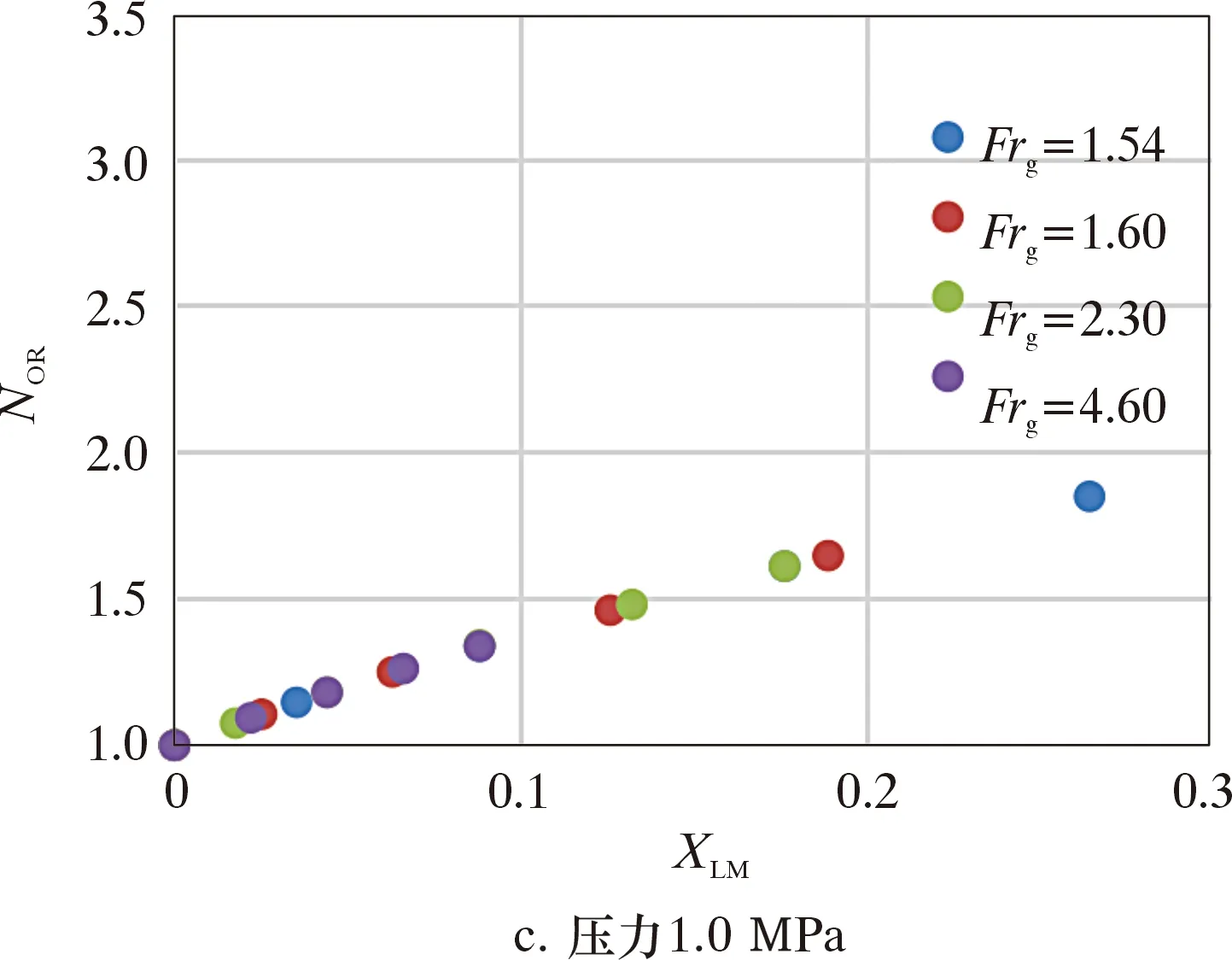
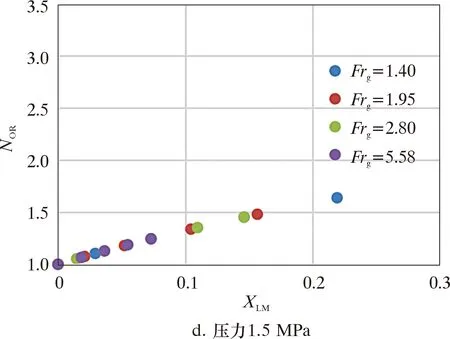
圖12 不同壓力下NOR與Frg、XLM的關系Fig.12 Over reading correction coefficient vs.Froude number Frg. in cases of different pressures

(3)氣液密度比(ρg/ρl)。數值模擬中不考慮溫度變化，氣相密度主要受壓力影響，液相密度在各試驗工況下基本不變，因此氣液密度比主要受氣相密度影響。0.2、0.5、1.0、1.5 MPa壓力下的ρg/ρL分別為0.003 5、0.007 0、0.012 9、0.018 7,ρg/ρL隨著壓力的升高而增大。圖13給出了不同氣相表觀速度vsg下NOR與ρg/ρL、XLM的關系。

由圖13可以看出，壓力條件相同時，隨著XLM變大，NOR的上升趨勢減緩；vsg相同時，壓力越大，ρg/ρL越大，NOR上升趨勢越緩；氣液兩相流的氣相流量越高，XLM越低，此時壓差的NOR也越低。

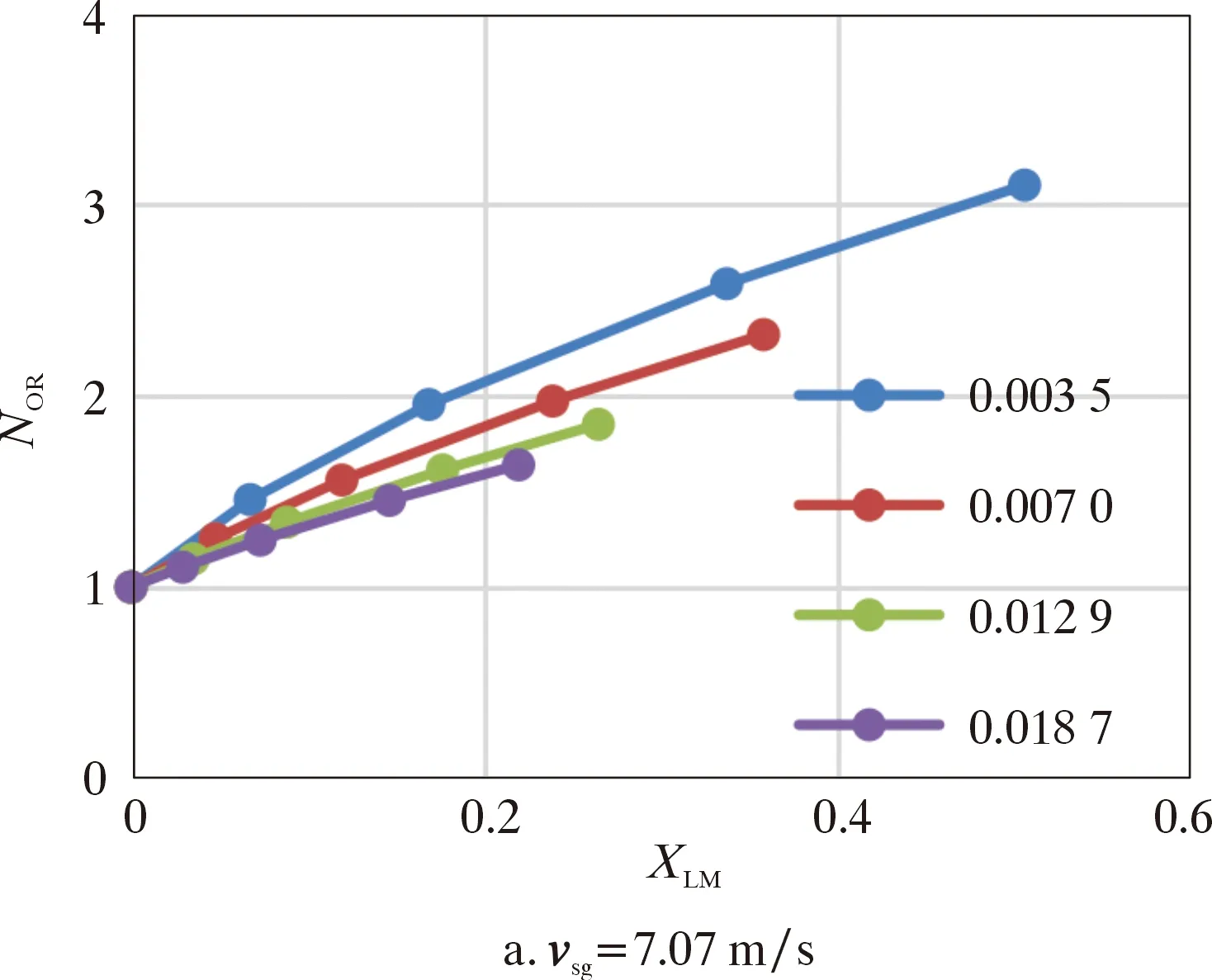
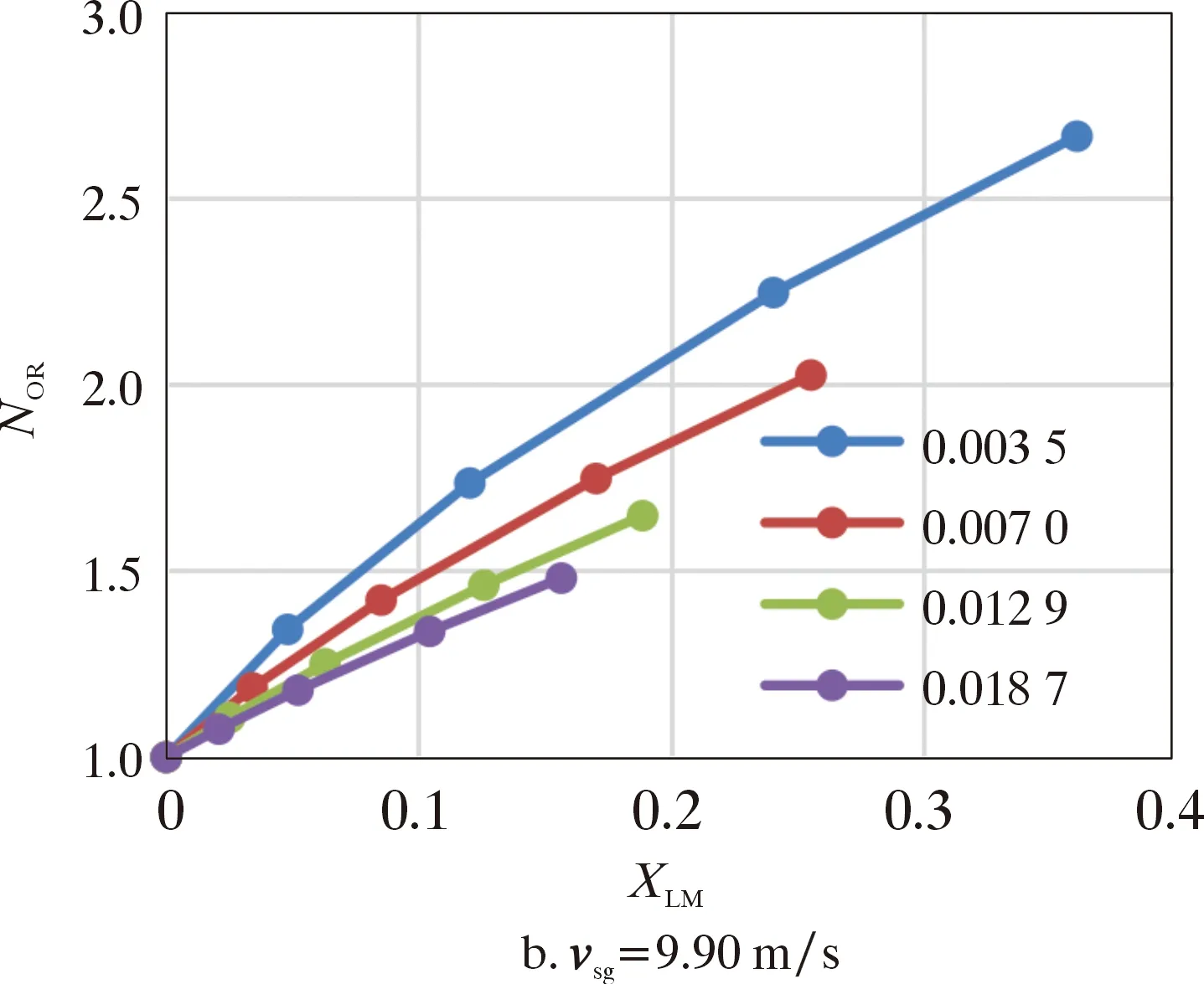
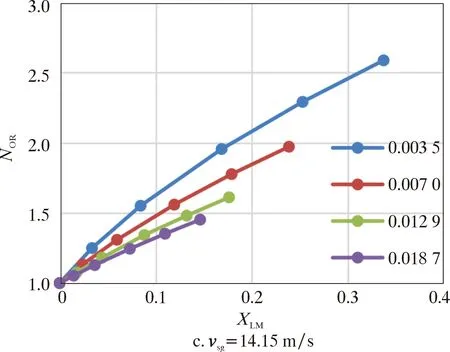
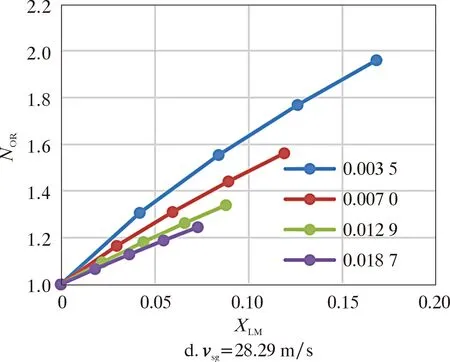
圖13 不同vsg下NOR與ρg /ρL、XLM的關系Fig.13 Over reading correction coefficient vs.ρg /ρl

3.2 不同虛高模型計算結果對比分析

繪制不同虛高模型計算得到的虛高圖，將軟件模擬得到的虛高與解析模型Smith and leang模型、Chisholm模型、De Leeuw 模型、林宗虎模型、Steven模型、均相模型、R-H模型、Steven孔板模型、StevenV錐模型的計算結果做對比分析，結果如圖14所示。

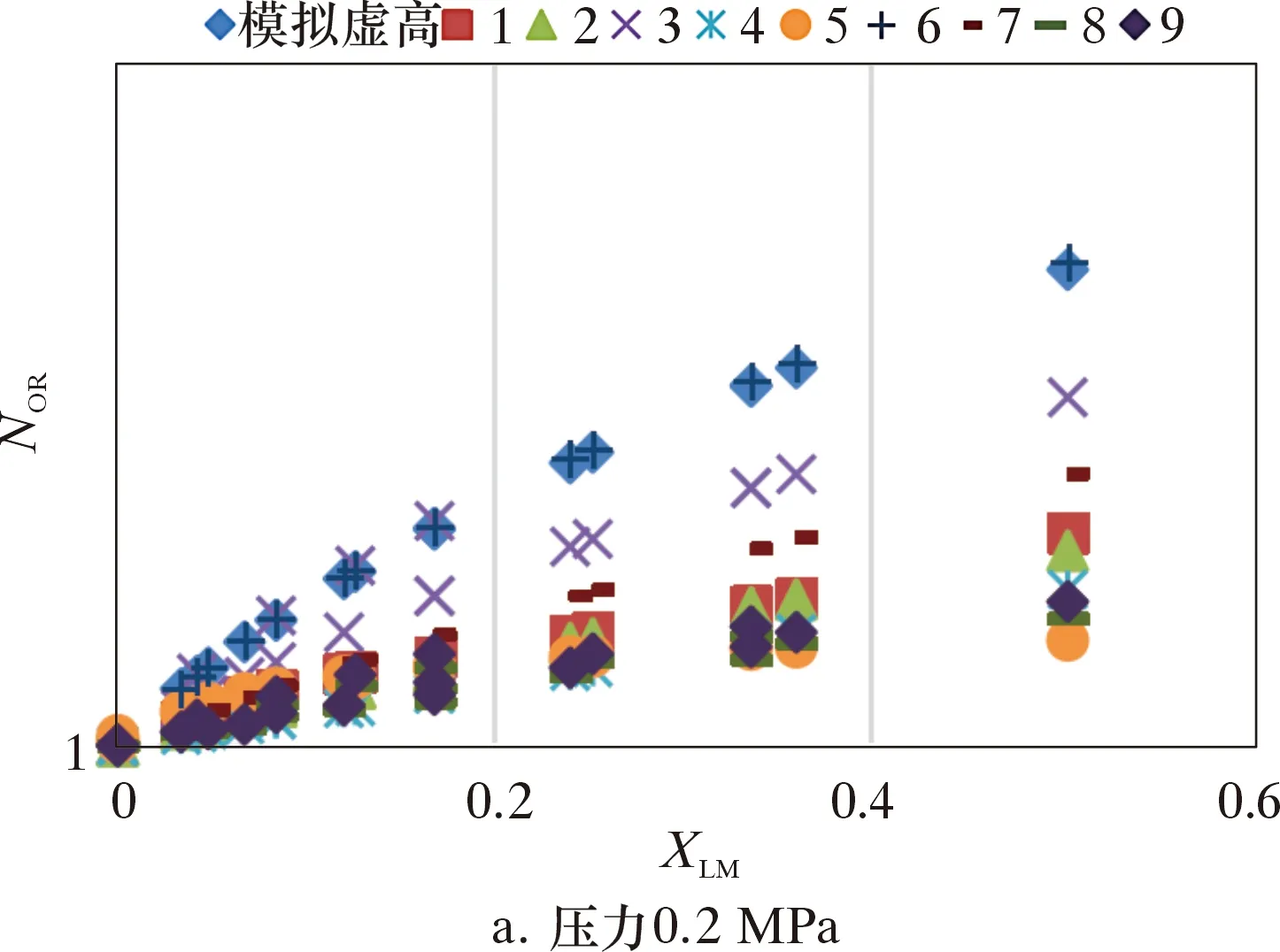
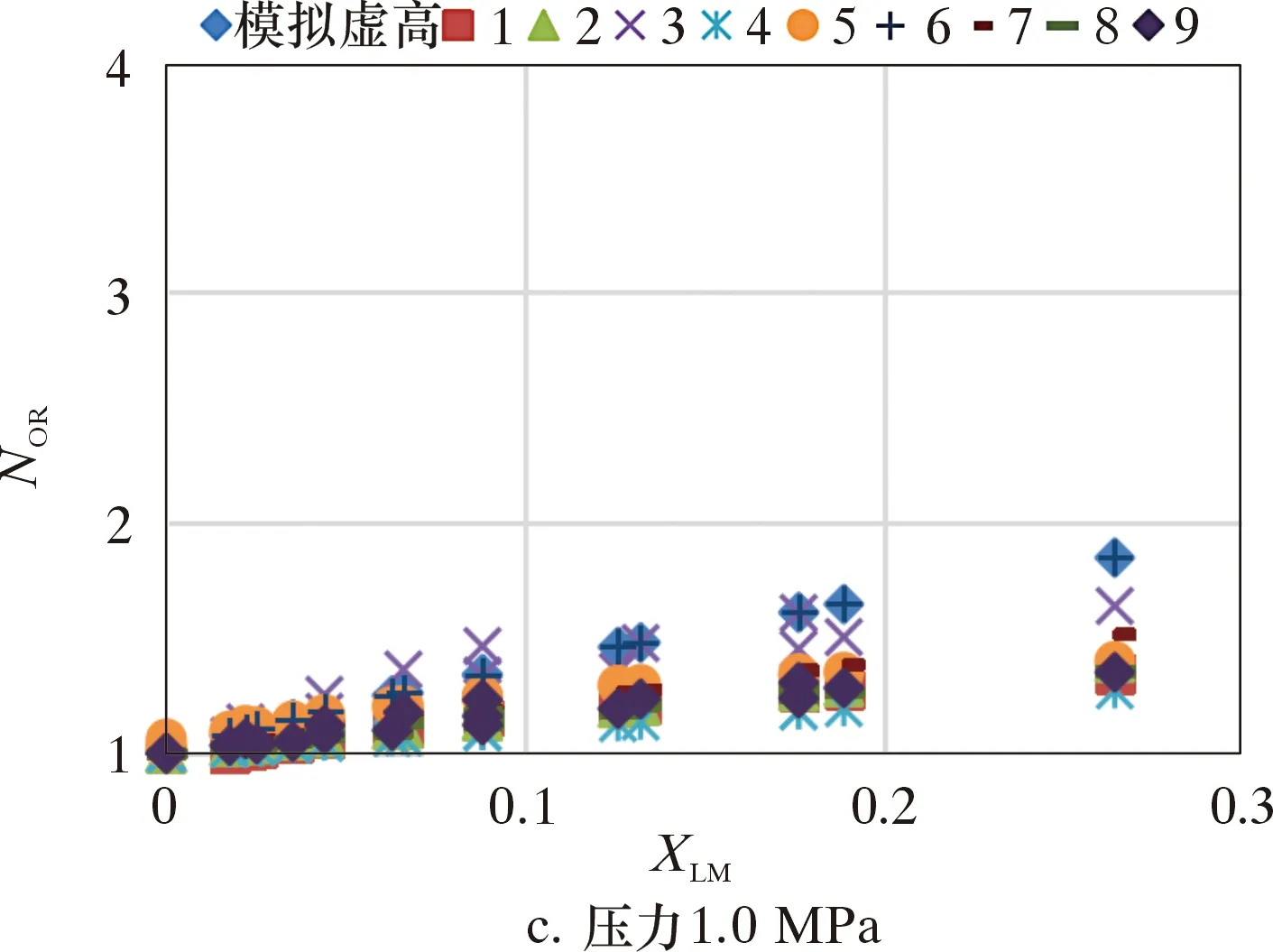
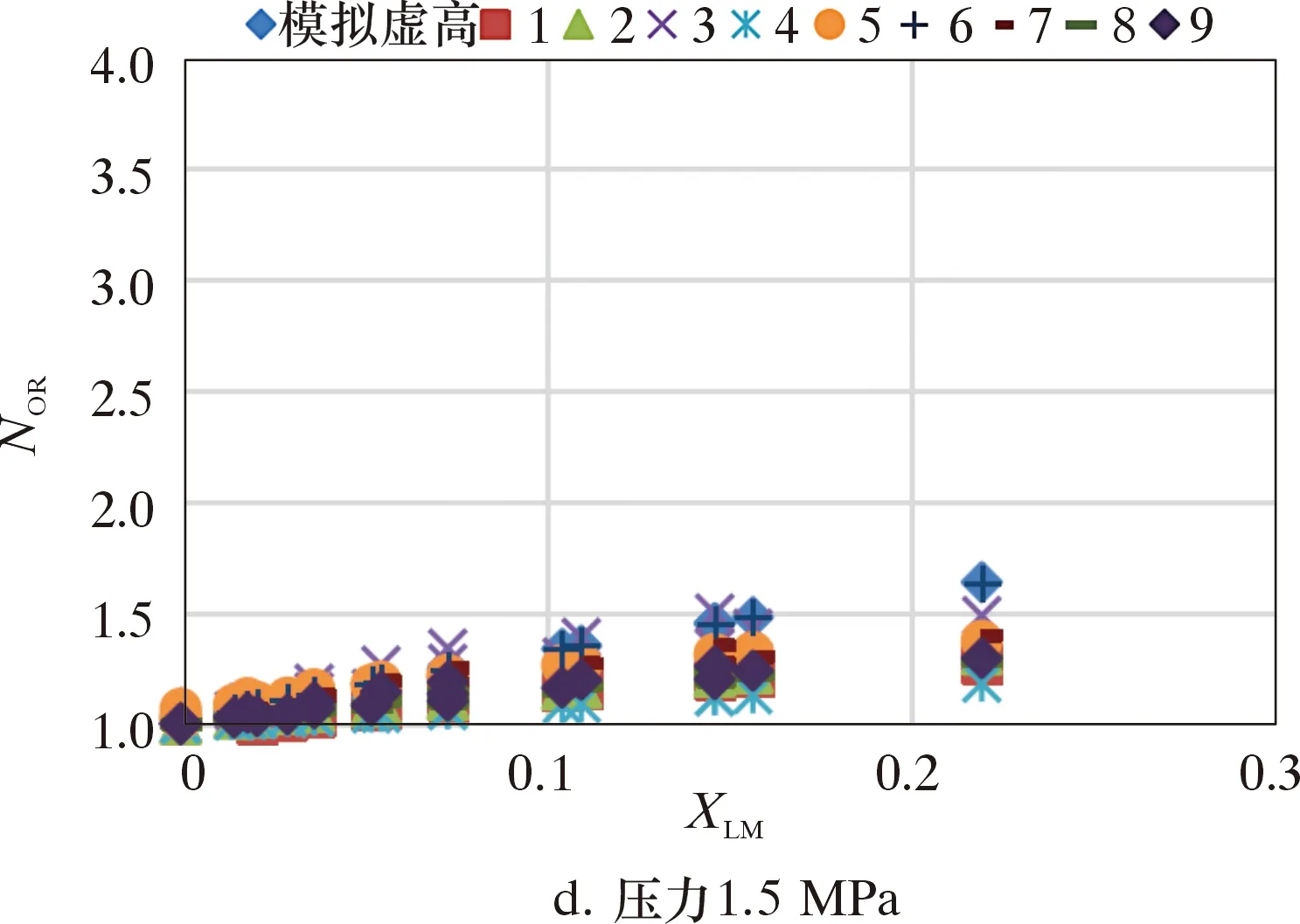
圖14 文丘里管不同虛高模型計算結果對比Fig.14 Comparison among different over-reading correction coefficient models for the Venturi tube

圖14中：1為Smith and leang模型；2為Chisholm模型；3為De Leeuw 模型；4為林宗虎模型；5為Steven模型；6為均相模型；7為R-H模型；8為Steven孔板模型；9為StevenV錐模型；模擬虛高是軟件模擬計算的虛高。

由圖14可知，數值模擬得到的虛高與各種模型計算的虛高隨壓力升高而降低。De Leeuw 模型、R-H模型、Steven孔板模型、StevenV錐模型的虛高修正指數n不確定，受Frg的影響。在試驗壓力較低為0.2 MPa時，Frg較小時，指數n取常數，上述模型計算所得的NOR與XLM呈線性關系。當試驗壓力到達0.5 MPa及以上時，在與低壓時相同的體積流量下，Frg會相對偏大，此時指數n為Frg的函數，上述模型的NOR與XLM不單為簡單的線性關系。均相模型在不同壓力下的NOR計算值都與數值模擬得到的NOR高度重合(見圖7)，這是因為數值模擬試驗中，氣液兩相為理想狀態，節流元件內各處的氣體與液體的體積分數都相同，達到了均相解析模型計算的標準前提，且多相流模型模擬時與均相流模型中都主要考慮了干度與ρg/ρL的影響。

4 結論及認識

(1)CFD仿真模擬單相氣流動、單相液流動與等質量氣液兩相的壓差對比，發現兩相流產生的壓差遠高于單相流。根據數值模擬結果提出以文丘里管壓損值建立虛高模型，文丘里管濕天然氣計量的虛高大小主要受壓力與液相含量的影響。

(2)數值模擬得到的虛高與各種模型計算的虛高隨壓力升高而降低。NOR隨XLM的增大而增大，兩參數成正相關。但隨著XLM增大，NOR不完全是XLM的函數。在工況壓力較低時，Frg較小時，NOR與XLM呈線性關系；當工況壓力增加，Frg會相對偏大，此時指數n為Frg的函數，NOR與XLM不單為簡單的線性關系。

(3)數值模擬試驗中設定氣液兩相的濕天然氣為均勻的理想流動狀態，且不考慮兩相的相互影響，即忽略了相間的影響。基于本文數值模擬獲得的虛高模型計算結果與均相虛高模型較相符，對實際濕天然氣計量有一定的實用價值。對于如何建立具有適應性強的虛高模型，需做進一步擴大模擬工況范圍的試驗研究。