基于TAN網絡的地鐵區間與車站施工事故致因分析

申建紅， 劉樹鵬

(1. 青島理工大學管理工程學院， 山東 青島 266520； 2. 青島理工大學城鄉建設信用與風險管理研究中心， 山東 青島 266520)

0 引言

地鐵作為城市化進程中高效快捷的出行方式，近年來得到迅速發展。由于地鐵施工開挖規模大、地下土質及管線情況復雜、施工工藝和技術要求高、風險因素眾多且多變，使得地鐵施工事故時有發生，并呈現增長趨勢[1]。因此，分析地鐵施工事故關鍵致因，從而為風險預防和控制提供決策支持，對保障施工安全至關重要。

目前，相關學者針對地鐵施工事故從多角度進行了廣泛研究。大部分學者采用主觀定性或半定性的方法展開分析，例如： 魏丹[2]將故障樹與層次分析法相結合，對造成豎井基坑圍護結構失穩的影響因素進行重要度排序； 鄭學召等[3]、周盛世等[4]分別采用梯形模糊層次法和基于PPC-D-S證據理論的方法，對地鐵施工風險等級進行評價； Liu等[5]采用調查問卷提取影響盾構施工安全的風險因素，為構建主客觀相結合的EFA-SEM風險分析模型奠定了基礎。為解決地鐵施工風險評估中專家認知的不確定性并有效聚合專家意見，Hou等[6]提出CNs網絡和EDAS的集成框架； 王乾坤等[7]研究了基于事故樹和相互作用矩陣的地鐵深基坑施工風險耦合評價方法。少部分學者采用客觀定量的方法進行研究，如于海瑩等[8]對地鐵施工期事故進行簡單統計分析，以揭示其內在規律； 李解等[9]、Xu等[10]通過對事故案例進行文本挖掘，識別出影響施工安全的關鍵致險因素； Zhou等[11]對5個方面的多源信息進行定量測量并融合，提出評價海底隧道施工風險等級的新方法，以實現對監測數據的有效利用。

上述研究成果對事故風險因素識別和風險等級評價起到了積極作用，但研究方法多為定性，其結果的準確性容易受到專家知識的主觀影響； 而現有的定量分析研究較少，且主要集中在對事故報告和案例的分析及對監測數據的利用。事故報告記錄了施工事故的詳細經過，建立方法與模型充分挖掘報告潛在的信息，可以對客觀定量研究方法進行補充。同時，關鍵致險因素識別多針對單一事故類型進行分析，少有模型對全部事故類型進行統一研究，且現有研究成果在實踐中的決策支持能力較弱。基于上述問題，本文在收集的202起事故報告數據的基礎上，采用樹增強樸素貝葉斯(tree augmented naive，TAN)和EM算法構建模型對數據進行分析，挖掘不同事故類型的針對性致險因素，并利用模型為事故預測和控制進行決策輔助，以期為地鐵區間隧道和車站施工事故風險預控提供支撐。

1 貝葉斯網絡與TAN網絡概述

1.1 貝葉斯網絡

貝葉斯網絡(Bayesian networks，BN)是基于圖論和概率論的一種有向概率圖模型，其可以利用不確定知識進行因果推理和風險預測，在海洋、化工等領域[12-13]的風險管理中已發展相對成熟。模型由風險節點、連接弧和條件概率表(conditional probability table，CPT)組成。風險節點代表各風險變量，連接弧反映節點間的條件依賴關系，CPT定義為子節點與父節點間的傳遞概率。BN中一組變量X=(x1，x2，x3，…，xn)的聯合概率分布P(X)可描述為

(1)

式中Pa(xi)是變量xi的父集合。

BN具有雙向分析能力，可以在給出新的證據E時更新節點概率[12]，節點的后驗概率如式(2)所示。

(2)

1.2 TAN網絡

TAN網絡是貝葉斯網絡的多種形式之一，包括1個類變量C和1個屬性變量A={A1,A2,…,AI}。其中： 類變量C包含m個狀態，由集合Sc={c1,c2，…，cm}表示； 每個屬性變量Ai(i=1,2,…,I)包含n個狀態，由集合SX={ai1,ai2,…,ain}表示[14]。TAN網絡克服了樸素貝葉斯網絡基于條件獨立性的假設，它允許每個屬性變量在有1個類變量作為父節點的基礎上，至多還可以有1個屬性變量作為父節點，考慮了屬性變量間的相互關系，如圖1所示。這與事故風險分析實際情況十分相符，各風險因素間具有內在聯系而非獨立存在，TAN網絡可以充分考慮這一點，以提高分析的準確性。

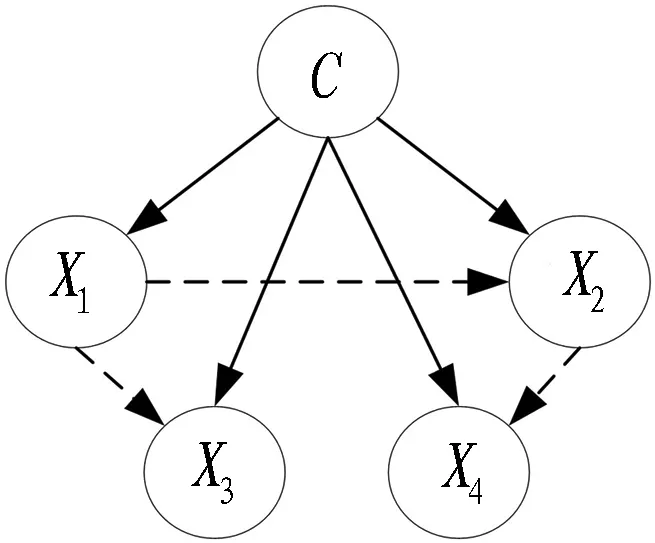
圖1 樹增強樸素貝葉斯網絡結構圖Fig. 1 Structure of TAN Bayesian

2 地鐵施工事故風險分析流程

采用TAN網絡模型對地鐵施工事故進行風險分析的技術路線如圖2所示。

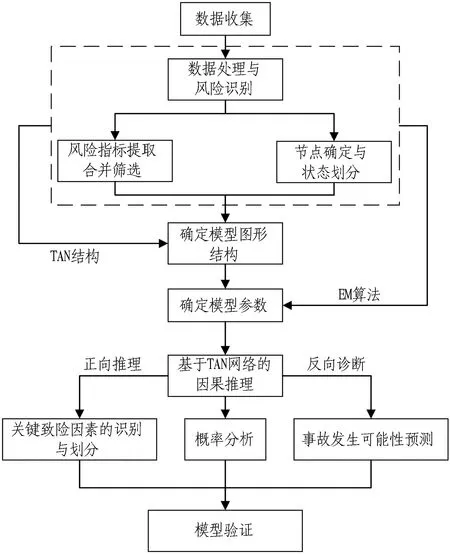
圖2 基于TAN網絡的地鐵施工事故風險分析流程Fig. 2 Risk analysis process of metro construction accidents based on TAN network

2.1 數據收集

數據收集范圍為國內2011—2021年間公布的地鐵施工階段事故報告，其中，東部城市約占數據總量的75%，中部城市約占數據總量的25%。大部分數據來源于政府網站，如各地應急管理局網站、安全生產監督管理局網站、住建部網站；少部分數據來源于網絡媒體，如百度文庫、新聞報道等。據不完全統計，初次共收集到220份事故報告。結合對報告內容的審查，剔除內容遺失和信息錯誤的事故報告，最終確定202份有效數據作為本文數據庫。

2.2 數據處理與風險識別

數據處理對提高機器學習性能至關重要。數據處理包括樣本重分類、特征選擇和屬性離散化等策略[15]，本文從3個步驟對數據進行處理，以完成風險識別。

2.2.1 風險指標提取及合并

從事故經過、直接原因、間接原因3個角度對風險因素的定性語言描述內容進行手動提取，同時記錄相對應的事故類型，實現初始樣本的重分類。基于事故報告內容并參考文獻[4，5，8-9],經一次提取，共得到4個事故經過因素(季度、發生時間、發生位置、施工工法)、62個直接因素、7個間接因素(安全交底培訓教育不到位、管理問題、安全隱患排查不到位、安全意識不足、監理失職、建設單位安全生產責任未落實、違法分包)、9種事故類型(坍塌、涌水涌砂、物體打擊、地面沉降、火災爆炸、高處墜落、管線破裂、機械傷害及其他)。

對于直接原因，由于事故報告對風險因素采用非結構化數據進行記錄，導致同一因素存在多種描述形式，在查閱GB 50715—2011《地鐵工程施工安全評價標準》并咨詢專家意見后，對同類風險因素進行歸類合并，經數據降維，最終得到24個直接風險因素。地鐵施工事故直接風險因素及說明如表1所示。

表1 地鐵施工事故直接風險因素及說明Table 1 Direct risk factors and descriptions of metro construction accidents

2.2.2 風險指標篩選

基于特征選擇的思想，指標過多會增加網絡的復雜性，而去除無關和冗余信息通常可以提高機器學習算法的性能，從而獲得具有良好預測性和計算密集度較低的模型[15]。因此，本文基于發生頻率對指標較多的直接因素和間接因素進行篩選，選取位于頻率均值之上的前10個直接因素和前5個間接因素用于模型構建。直接因素和間接因素的發生頻率分別如表2和表3所示。

表2 直接因素的發生頻率Table 2 Frequency of direct factors

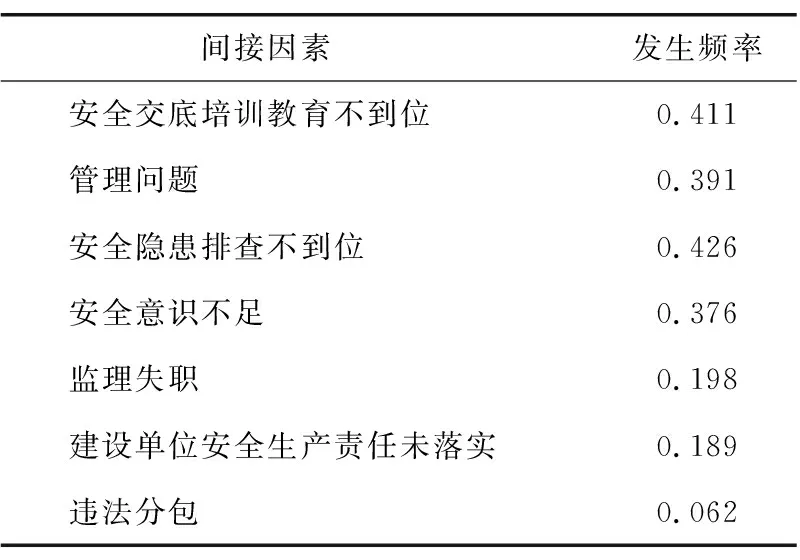
表3 間接因素的發生頻率Table 3 Frequency of indirect factors

2.2.3 節點確定與狀態劃分

將篩選后的風險指標和事故類型確定為模型節點，同時根據事故數據內容將節點屬性離散為不同狀態，各節點代號及狀態劃分如表4所示。

表4 各節點代號及狀態劃分Table 4 Identification and status division

2.3 TAN網絡結構學習

TAN網絡結構學習本質上是一個優化問題，其利用信息論中2個屬性變量在給定類變量下的條件互信息來定義網絡結構[16]，將事故類型定義為類變量，其余風險因素定義為屬性變量。屬性之間的條件互信息計算如式(3)所示。

IP(Ai;Aj|C)=

(3)

式中：IP表示條件互信息；aii是風險因素Ai的第i個狀態；aji是風險因素Aj的第i個狀態；ci是事故類型的第i個狀態。

網絡結構學習過程如下[16-17]:

1)計算地鐵施工風險分析中每對屬性變量之間的條件互信息IP(Ai;Aj|C)，i≠j。

2)建立1個以全部屬性變量兩兩相連成弧、弧權重為IP(Ai;Aj|C)的完全無向圖。

3)找出最大權重生成樹。

4)從屬性變量中選擇1個根變量，并將所有邊的方向設置為向外，將生成的無向樹轉換為有向樹。

5)添加1個由類變量C標記的頂點，并為每個Ai添加1條從C出發的弧來構建TAN模型。

2.4 TAN參數學習

模型參數學習包括確定節點先驗概率和轉移概率2部分。學習過程基于事故數據庫和網絡圖形結構，采用參數學習算法并借助軟件完成訓練。考慮到已有數據可能存在缺失值的情況，為降低缺失值對參數精確度的影響，本文采用EM算法。該算法在應對數據缺失情況時具有良好的性能[18]，其完整參數學習過程如下。

分別定義不完整數據集D=(l1,l2，…，lM)和完整數據集Y=(c1,c2,…，cM)，D∈Y。設ζ=(V,E,P)是具有參數Θ={Θq}的BN，其中Θq={Θqs}且Θqs={Θqst}，滿足對于每個q,s,t，都有Θqst=P(Xq=t|pa(Xq)=s)。基于初始化參數算法，不斷交替迭代E步和M步逼近最優。

1)E步通過式(4)和式(5)建立1個完整的數據集Y。

(4)

(5)

式中：Mqst是(Xq,pa(Xq))=(t,s)的計數；lq是D的第q種情況。

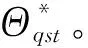
(6)

E步和M步交替迭代直至2個連續迭代的對數似然差不超過閾值δ乘以對數似然的值，即k(Θ)收斂，如式(7)所示。

kq(Θ)=kq+1(Θ)≤δ|kq+1(Θ)|。

(7)

式中：kq(Θ)為第q次迭代后Θ的對數似然；kq+1(Θ)為第q+1次迭代后Θ的對數似然。

2.5 基于TAN網絡的因果推理

2.5.1 概率分析

參數學習后的模型可以推理各節點不同狀態的發生概率，對不同事故類型和風險因素進行概率分析，可得到一般統計分析下的初步風險認知。

2.5.2 正向推理

將事故類型節點不同狀態設置為100%，利用貝葉斯網絡正向推理能力，對各風險因素節點進行敏感性分析，可以識別出關鍵致險因素。對于只有2個狀態的節點，可以計算節點變化前后的風險變化(variation of risk, ROV)，根據ROV值的大小對風險的重要程度進行排序[19]，該方法對于具有2個以上狀態的變量存在無法界定是哪2個狀態的不足。基于此，本文引入真實風險影響(true risk influence，TRI)[20]，分析風險因素對事故類型的重要程度。該方法首先將變量全部狀態分別設置為100%，然后根據事故類型節點后驗概率分別記取對事故影響最大的狀態，即高風險推斷(HRI)，以及對該事故產生最小影響的狀態，即低風險推斷(LRI)。通過計算HRI和LRI的平均值，得出每種風險因素對此類事故的TRI，根據TRI值大小對風險因素進行重要度排序，如式(8)所示。

(8)

2.5.3 反向診斷

將不同事故場景下已知的風險因素狀態作為證據輸入模型，利用貝葉斯網絡反向診斷能力，對可能發生的事故類型及發生概率進行預測，結果可為事故相關方的風險預防提供決策支持。同時，可將正反向推理相結合，在特定事故類型發生后，將事故類型和已探明的風險因素狀態同時輸入模型，以便快速識別事故發生的最可能風險源，為風險控制提供支持。

2.6 模型驗證

考慮到樣本數據量較少，為充分利用樣本信息，本文采用10折交叉驗證方法對模型的有效性進行檢驗。該方法允許使用相同的數據集驗證模型，通過將數據集劃分為大小相等的10部分，輪流將其中9份作為訓練集，其余1份作為測試集，訓練和測試數據重復10次，取10次正確率的平均值為驗證結果。同時，可根據接受者操作特性曲線(ROC曲線)判別模型的性能[21]，具體見3.2節。

3 結果分析和模型驗證

借助GENIE軟件對202起事故數據進行結構學習和參數學習，最終得到完整的地鐵施工事故風險分析模型，如圖3所示，利用此模型并按照2.5節流程對地鐵施工事故進行多角度分析。

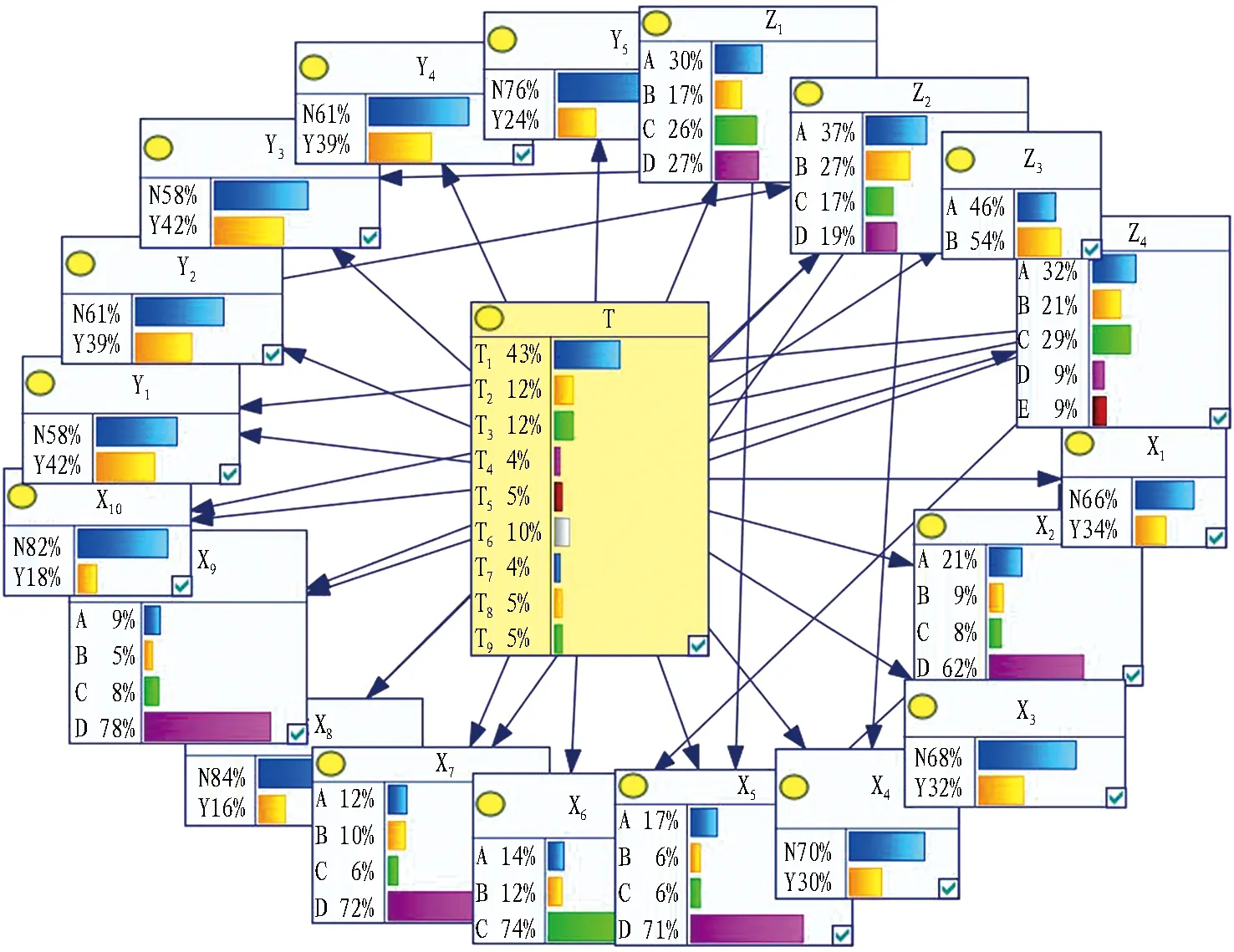
圖3 地鐵施工事故風險分析的TAN模型Fig. 3 TAN model for risk analysis of metro construction accidents

3.1 結果分析

3.1.1 概率分析

根據圖3對各節點進行概率分析，得出初步風險認知。

1)事故類型節點的概率分析。坍塌(T1)在地鐵施工事故中有著最高的發生率43%，其次是涌水涌砂(T2)和物體打擊(T3)，約為12%，高處墜落的發生率約為10%，其他事故類型的發生率為4%～5%。這與文獻[1]和文獻[8]有著相似的結論，其中涌水涌砂事故在分析中較其他文獻發生率較高，這可能與統計樣本選擇不同有關，本文數據來源于東部沿海城市的樣本比例較大，受地理位置影響，涌水涌砂事故發生率較高。

2)事故經過因素的概率分析。每年的4—6月份事故發生率最低，為17%，其他月份為26%～30%，這與夏季和冬季的不利氣候條件密切相關。在一天的時間中，00：00—05：59有著最高的事故發生率，為37%； 12：00—17：59事故發生率最低，為17%。在發生位置方面，區間事故發生率(54%)略高于車站事故發生率(46%)。在施工工法方面，明挖法和盾構法事故發生率較高(分別為32%和29%)，其次為暗挖法(21%)，而其他工法事故發生率較低。

3)事故直接因素的概率分析。地質條件差、施工方案執行問題、支護系統失效、違章施工的事故發生率在30%以上，對事故的發生有重要影響；應急處理措施不當、勘察設計錯誤、施工技術問題和臨邊荷載過大的事故發生率在20%～30%，對事故的發生也有較大影響；水文條件差和不良天氣事故發生率小于20%，影響相對較小。

4)事故間接因素的概率分析。安全交底培訓教育不到位和安全隱患排查不到位是事故發生率最高的間接因素(42%)，其次是管理問題和安全意識不足(39%)，監理失職的事故發生率較低(24%)。

3.1.2 基于TAN的正向推理

根據TRI的定義及式(8)計算風險因素和全部事故類型的TRI值，如表5所示。

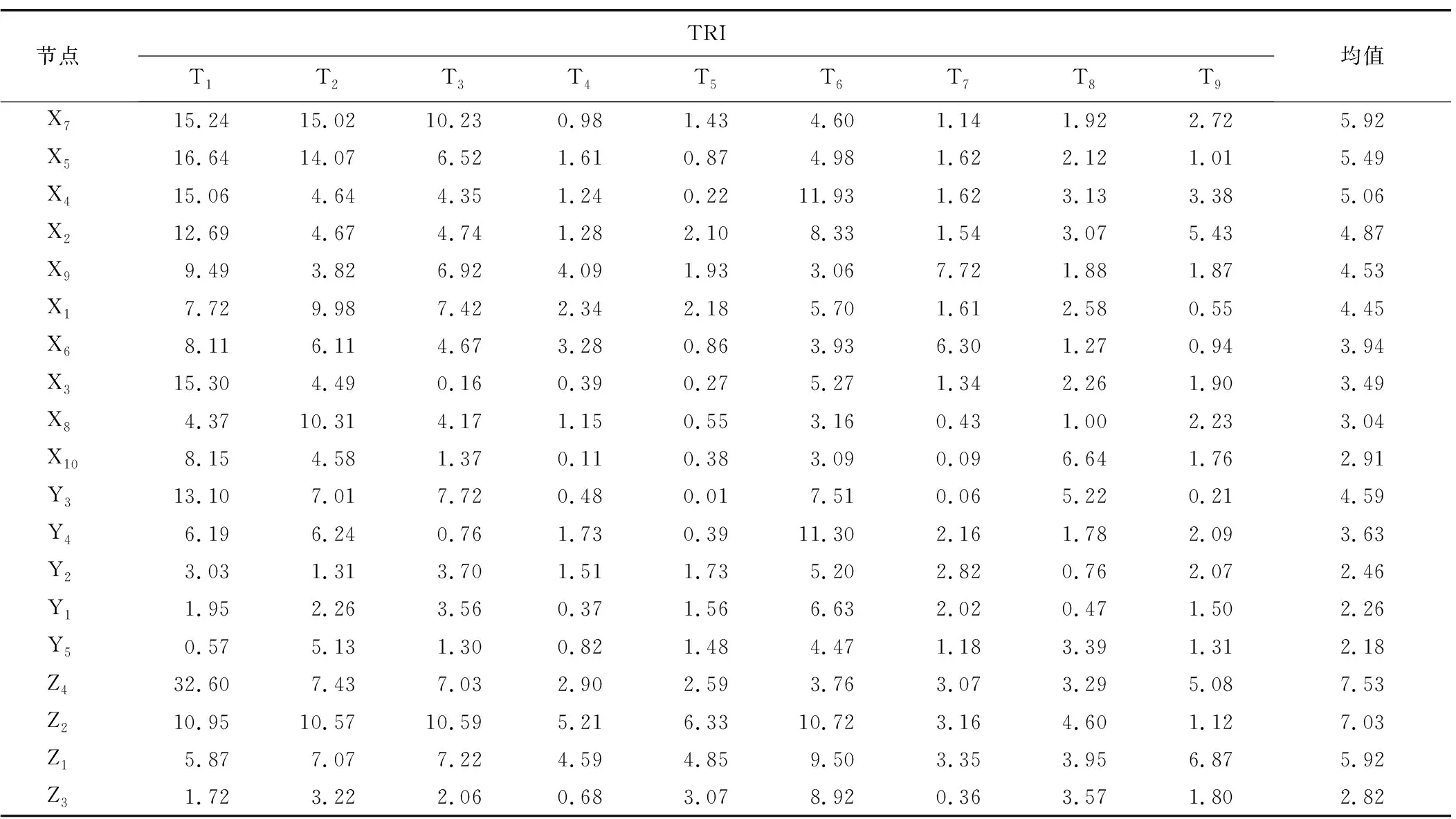
表5 事故類型和風險因素的TRI值Table 5 True risk influence of accident types and risk factors

TRI的均值可以反映風險因素對地鐵事故發生的總體影響程度。在直接因素方面，施工技術方法不適用、專業水平低(X7)，缺乏應急處理措施或不及時、不適用的處置措施(X5)，違章施工(X4)對事故的發生有著關鍵作用； 其次是施工方案(X2)、臨邊荷載過大(X9)和地質條件差(X1)；其他風險因素相對影響較小。在間接因素方面，安全隱患排查不到位(Y3)是最關鍵的因素，其次是施工及管理人員缺乏安全意識(Y4)，管理問題(Y2)、安全交底培訓教育不到位(Y1)和監理失職(Y5)相對影響較小。在事故經過方面，引發施工事故的風險因素重要度排序為： 施工工法(Z4)、發生時間(Z2)、季度(Z1)、發生位置(Z3)。與概率分析得到的初步風險認知相比，基于TRI均值的分析考慮了各節點間的相互作用，分析結果更加貼近實際。

根據事故類型與風險因素的TRI值，對不同事故類型的風險因素進行重要度排序，如表6和表7所示。以坍塌事故(T1)為例，其直接風險因素重要度排序為： X5>X3>X7>X4>X2>X9>X10>X6>X1>X8。在預防坍塌事故發生中，應按照風險因素重要程度制定針對性措施，應對應急處理措施、支護系統安全、施工技術水平、違章施工等排序靠前的因素予以更多的關注。其間接風險因素重要度排序為： Y3>Y4>Y2>Y1>Y5。在日常巡查及施工安全管理中，應著重加強對安全隱患的排查，防止施工事故的發生。其事故經過因素重要度排序為： Z4>Z2>Z1>Z3。施工工法和發生時間相對于季度和發生位置對事故影響作用更大，在事故風險研究中可按照重要程度優先依次分析。

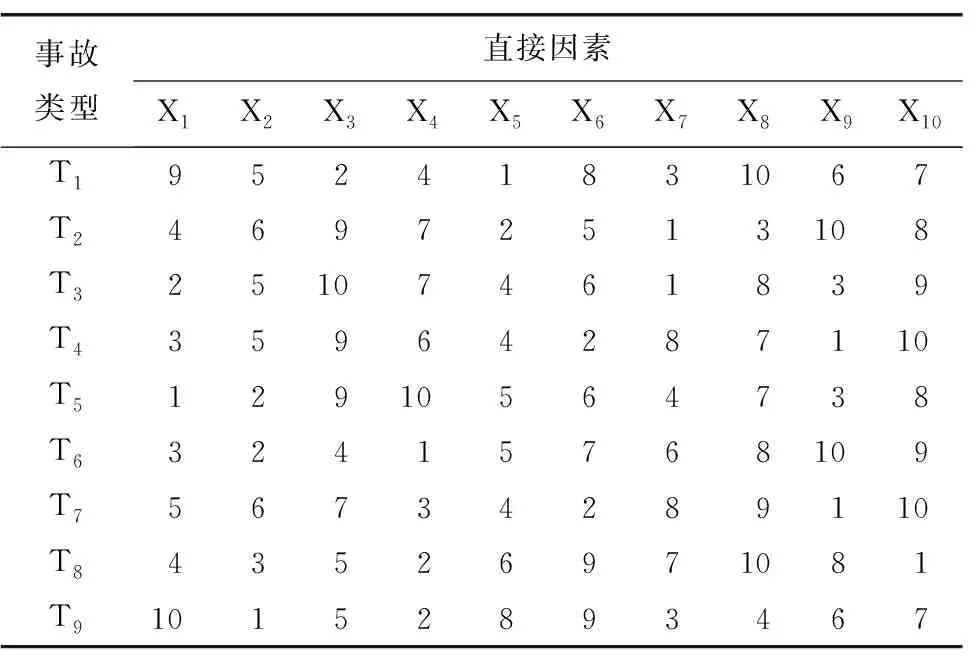
表6 不同事故類型對應直接風險因素重要度排序Table 6 Importance ranking of direct risk factors corresponding to various accident types

表7 不同事故類型對應間接風險因素和事故經過因素重要度排序Table 7 Importance ranking of indirect risks and accident process factors corresponding to various accident types

3.1.3 基于TAN的反向診斷

為探究不同風險因素組合對事故發生的影響，通過實際案例對該模型在風險預測方面的支持作用進行說明。某涌水涌砂事故為區間施工項目，發生時間為2012年9月12日01：00左右，采用盾構法施工，事故發生前因遭遇未探明的不良地質水文條件，便安排現場施工人員進行圍擋加固處理，但因加固處理施工方法不當且現場安全監理未及時發現隱患，導致涌水涌砂事故發生。將上述證據輸入模型，結果如圖4所示。

圖4 風險組合下的預測模型Fig. 4 Prediction model under various risk combinations

模型預測結果顯示，有85%的概率會發生涌水涌砂事故，預測結果與實際事故一致，說明了該模型對風險預測的積極作用。施工方或其他利害相關者可以以此模型作為風險預測和風險控制的決策輔助工具，以降低施工事故帶來的不良影響。

3.2 模型驗證

以事故類型為檢測節點，借助GENIE軟件對數據集進行10折交叉驗證，結果顯示此模型的正確預測率為89.6%，表明該模型具有較好的參考性。樣本驗證詳細結果如表8所示。

表8 樣本驗證詳細結果Table 8 Detailed results of sample validation

ROC曲線同樣能反映模型的性能，通過ROC曲線的曲線下面積(AUC)來評估，AUC值越大，表明模型的性能越好，一般認為AUC值在[0.85，0.95]的模型具有很好的性能[22]。以事故類型節點T5狀態為例，其AUC值為0.856，表明模型預測具有較高的準確率，T5的ROC曲線如圖5所示。對于部分節點狀態，如T7存在AUC值過高(為1)的情況，這是由于此類型數據較少(僅有7起)，需在今后的研究中通過收集更多的數據量進行重新評測。

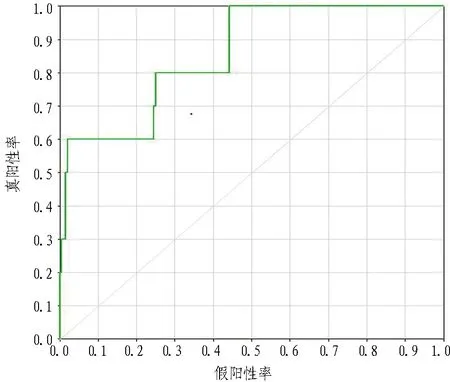
圖5 事故類型T5狀態的ROC曲線Fig. 5 ROC curve for accident type in T5 state

4 結論與討論

1)借助TAN網絡和EM算法，構建地鐵施工事故致因分析模型，對2011—2021年間的202起事故數據進行訓練學習，所建模型實現了對事故報告潛在信息的挖掘和利用，采用客觀數據從3個角度對地鐵施工事故進行深入分析，避免受專家知識的主觀影響。

2)基于模型分析，明確了不同類型事故的關鍵致險因素，并對各風險因素造成事故發生的總體影響程度進行重要度排序，豐富了地鐵施工安全事故管理理論； 該模型可將實際工程項目的已知信息作為證據輸入，為風險預防和控制提供決策支持，同時可為類似工程的事故報告挖掘和致因分析提供參考。

3)限于樣本數量較少，模型的準確率及部分節點狀態的AUC值有待改進，未來將收集更多的數據用于提高模型性能，以期為減少地鐵事故發生提供更多支撐。