基于GeoGebra的深度學習教學設計與思考
——以蘇科版八年級上冊“一次函數的圖象(1)”為例*

蔣余希 李明樹 (江蘇省蘇州工業園區東沙湖實驗中學 215021)

1 緣起

《義務教育數學課程標準》(2022年版)(以下簡稱《課標2022年版》)指出要促進信息技術與數學課程的融合：合理利用現代信息技術，提供豐富的學習資源，設計生動的教學活動，促進數學教學方式方法的變革[1].而蘇科版八年級上冊“一次函數的圖象(1)”[2]教材中“燒香”實驗操作性不強且脫離實際，很難引起學生對新知的感悟.故基于課標及學生認知需要，選取新素材用“做”數學的策略，有效使用信息技術，培養學生深度學習能力，提升學生思維層次，涵育數學核心素養.

1.1 GeoGebra與數學教學

信息技術的融合是基于課堂需要來選擇功能切實的軟件，使其各展所長[3].近年來，免費且實用的數學軟件GeoGebra越來越多地出現在數學教學實踐中，其以強大的動態幾何、代數運算和概率統計功能為數學課堂提供更多元的可能.而本課依托GeoGebra代數區和繪圖區功能完成了一次函數圖象的可視化，使“數”與“形”完美融合.

1.2 深度學習與核心素養

學習是把信息和經驗轉化成知識、技能、行為和態度的終身過程.而深度學習是在教師指導之下，圍繞具有挑戰性的學習主題，積極地探究實踐，深刻地掌握學科的核心知識，并運用知識解決問題，形成積極的內在的學習動機、高級的社會性情感、積極的態度、正確的價值觀[4].這與《課標2022年版》提倡的核心素養導向高度吻合，故深度學習是全面深化課程改革、落實核心素養的重要路徑.

2 教學過程

2.1 回顧·整理

回顧小組交流并完成知識框架圖.(師生合作圖1)

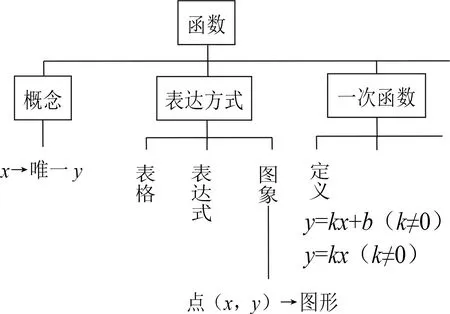
圖1

設計意圖以活動驅動，復習整合，喚醒舊知，為本課作鋪墊.

2.2 生活·數學

情境 用60 cm的繩子圍長方形OABC，如圖2，設OC=xcm，OA=ycm，觀察y隨x的變化而變化的情況.

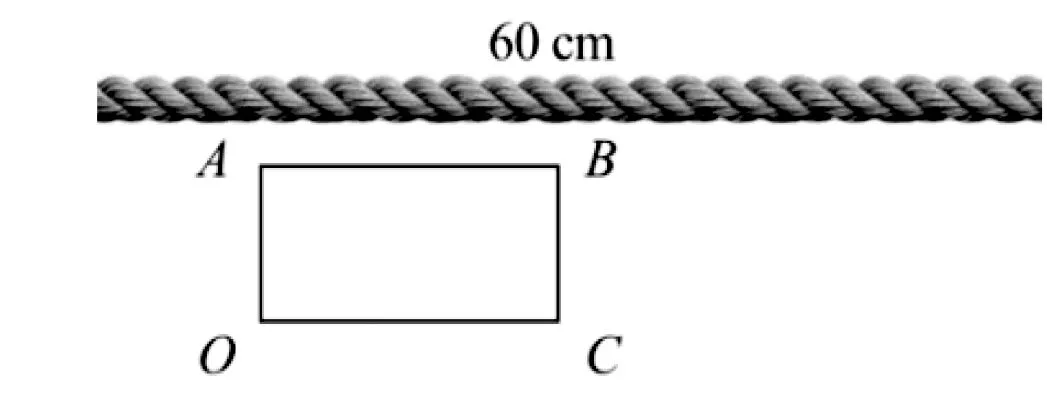
圖2

填入表格中y的值，并觀察思考：

x/cm510152025y/cm252015105

(1)y隨x的變化是如何變化的？

(2)x和y有什么不變的關系？用數學式子表示.

發現y是x的一次函數，表格里是x+y=30的5組解.這5組值滿足一次函數y=-x+30，是函數圖象上的5個點.

設計意圖由熟悉的長寬問題引入，在變與不變的關系中引發思考，感知規律的“式”、表格的“數”以及一次函數“圖象”上點之間的關聯及一一對應關系.在實際問題數學化的過程中滲透數形結合思想.

2.3 操作·發現

活動1釘板圍長方形

規則借助表格和素材(一塊含磁吸的透明釘板及若干等長彩色皮筋)，圍周長為60的長方形，使得：

(1)長方形的頂點O與坐標原點(釘板左下角的釘)重合；

(2)OC落在x軸上，OA落在y軸上；

(3)釘板相鄰兩釘的距離和平面直角坐標系單位長度均為5.

要求：安全、合作、思考.

圖3 圖4

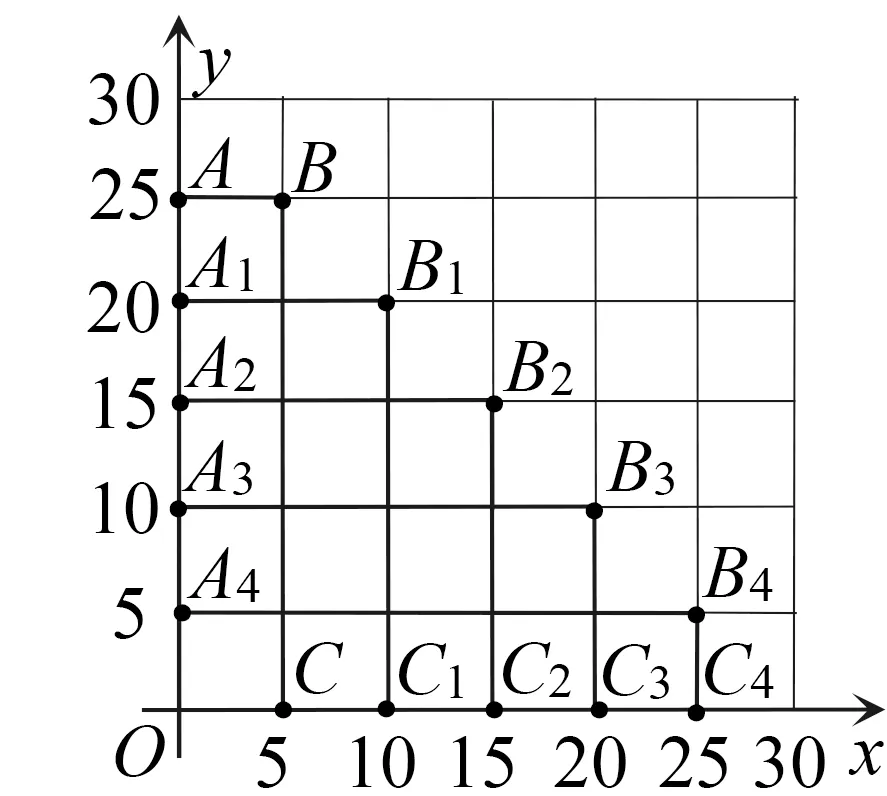
圖5

設計意圖學生通過“做”數學觀察一次函數圖象上有限個點的位置關系.用直尺靠，用眼睛看，激發學習的積極性和研究力，拓展思維深度，培養合作精神.

猜想：滿足一次函數y=-x+30的點B,B1,B2,B3,B4在同一直線上.

師：你能證實此猜想嗎？

生：拿尺子靠，這5個點在一條直線上；過兩點畫直線，看另外三點在不在這條直線上；證全等.

師：再給出周長60但長未知的矩形(圖4)，思考頂點B5是否滿足上述猜想.

師：(引導)B5坐標滿足y=-x+30嗎？(生：滿足)所以它是函數圖象上的點.拋開實際問題，y=-x+30中x可以取哪些值？(生：任意實數)

設計意圖初步形成“一次函數圖象上有限個點好像在同一條直線上”的認知后，提出問題“無限個點的位置如何”，引導學生深度學習，大膽猜想并嚴謹求證.

2.4 探究·感受

有限點不能確定一次函數圖象，需繼續描點觀察，GeoGebra可以輔助實現[5].

操作過程：

(1)將坐標調整到單位長度為1，列表動畫按鈕，描點動畫按鈕，學生觀察這一系列點的位置關系.問學生0～1之間還有距離嗎？能不能繼續取值？得到肯定回答，繼續操作；

(2)將坐標縮小到單位長度為0.1，同上操作.問0～0.1之間還有距離嗎？學生猜測，繼續操作；

(3)將坐標縮小到單位長度為0.01，同上操作.

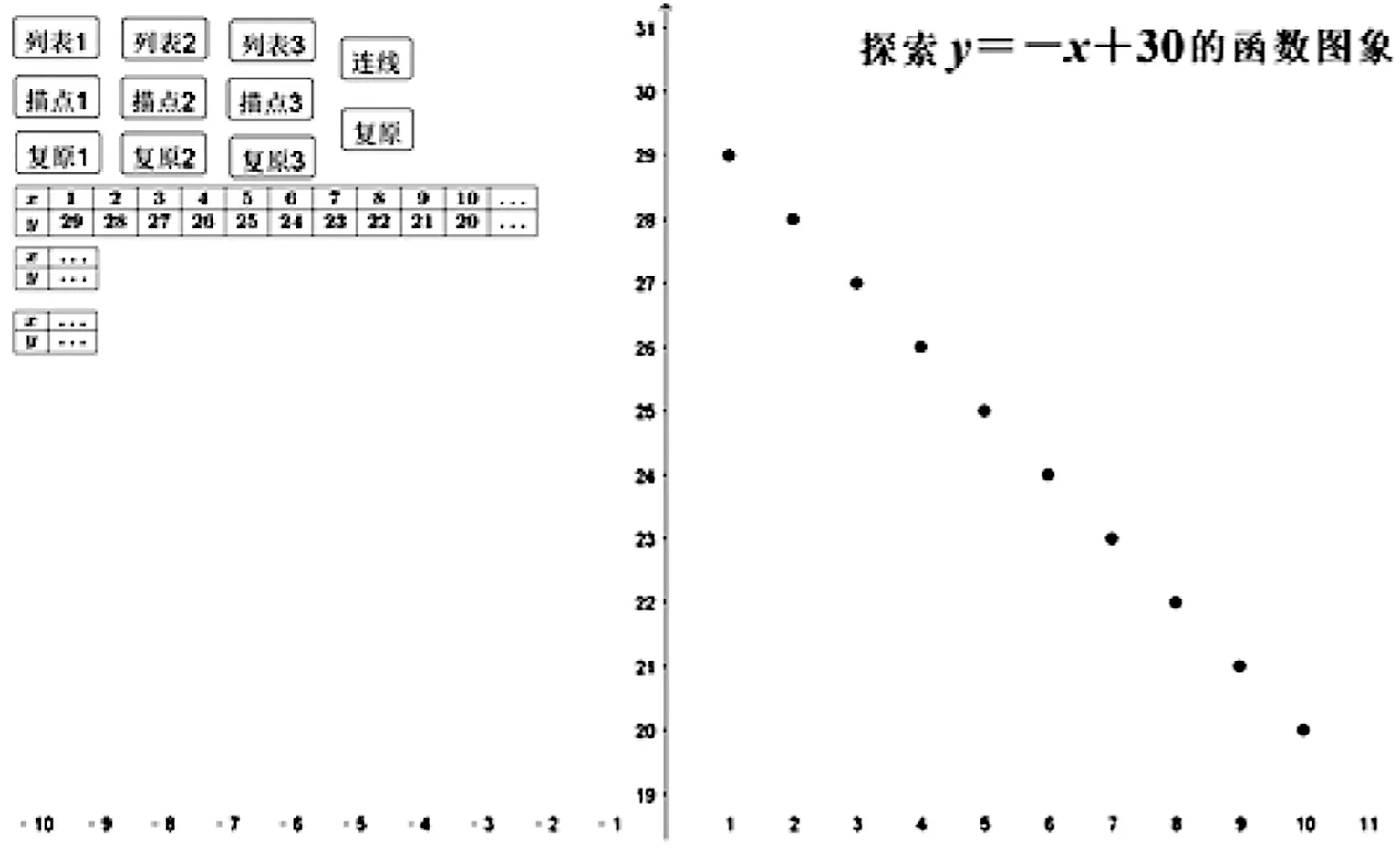
圖6

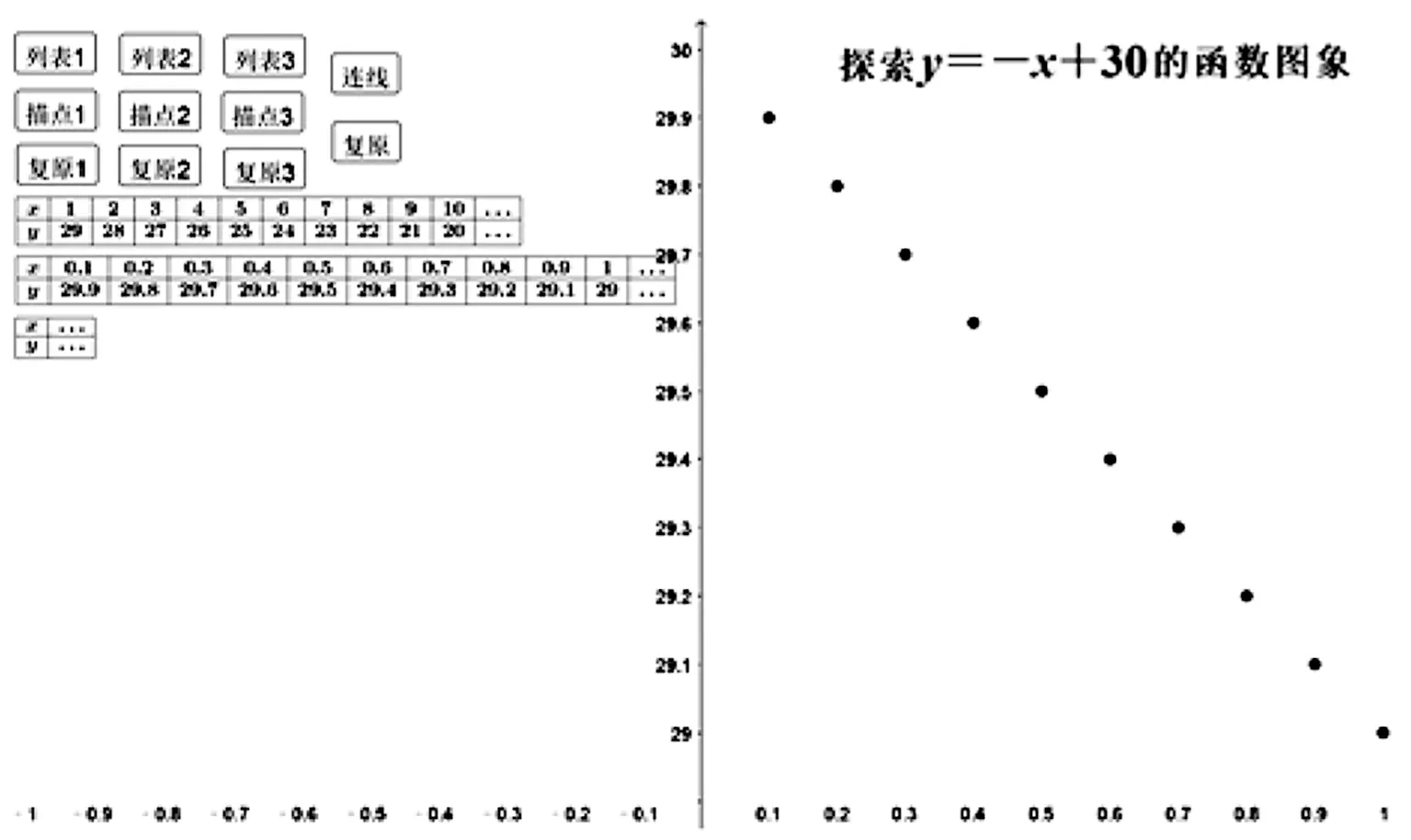
圖7

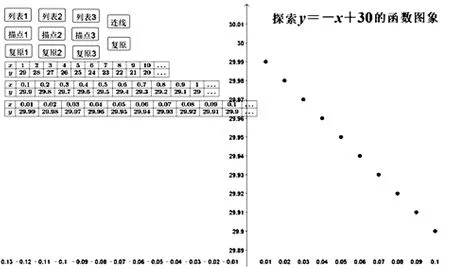
圖8

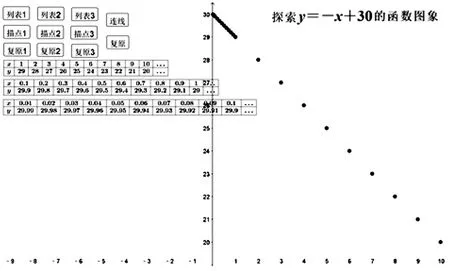
圖9

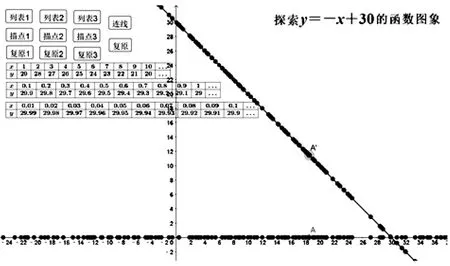
圖10

結論若持續操作，圖象將逐漸清晰，發現函數圖象上的點都在同一條直線上.

操作過程：

(4)將坐標逐漸放大時，發現點與點“緊密地挨在一起”；

(5)通過繪制點A(x，30-x)的軌跡，深化學生認識：一次函數的圖象是一條直線.

(6)連線按鈕，繪制圖象.

師：根據研究y=-x+30圖象的經驗，總結如何得到一次函數的圖象？

生：一列表，二描點，三連線.

師：這個作圖方法叫作——描點法.(提醒要寫上函數名)

設計意圖GeoGebra縮小坐標軸的單位長度至作圖需要的x范圍后，描點觀察位置；再放大坐標軸的單位長度，動態過程中點慢慢地緊密地挨在一起.把抽象的加密取點過程可視化，使學生能夠完全理解并參與，研究過程更充分，知識生成更自然，真正以學生為主體，使課堂“動”起來，使學生學“活”的知識.

2.5 實踐·歸納

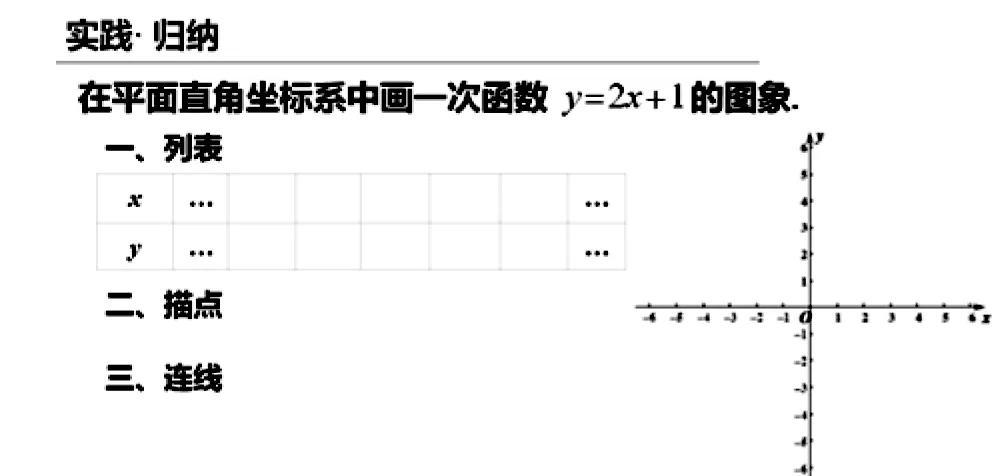
圖11

活動單：畫y=2x+1的圖象.(投屏討論)

預設師：表格里…是什么含義？

生：省略，畫不完所有的點.

生：沒有兩邊延伸.

師：數學是講究美的學科，對稱取點可避免圖象只有一邊的問題.

生：沒有標函數名；描點沒有描.

師：標上表達式更清晰；過x=1，y=5作垂線交于一點.

設計意圖發現式學習由學生獨立嘗試，發現問題再集中糾偏，基于學生的最近發展區建立作圖規范.

2.6 交流·思考

繼續討論函數圖象畫法，通過思考直線特征得到更簡便的“兩點法”.

活動2 合作繪圖

圖12 KT板尺寸35 mm×50 mm

提前制作好輕便、展示性強的KT板，小組合作再畫y=2x+1的圖象及一個組內自選函數.

教學預設為了兼顧分布狀態，大多取便于計算的坐標軸交點.

師：對一般形式y=kx+b，你能說出與坐標軸的交點嗎？

師：那y=-6x+1如何取點？

生：不好畫.

師：如果坐標軸交點不好畫，可取整數格點.

設計意圖基于深度學習理解與批判特征，繼續深化討論取點的技巧.在自選函數過程中作出正比例函數和與原函數平行的函數時，可對圖象性質稍作拓展.KT板小組作圖強化學習的獲得感和成就感.

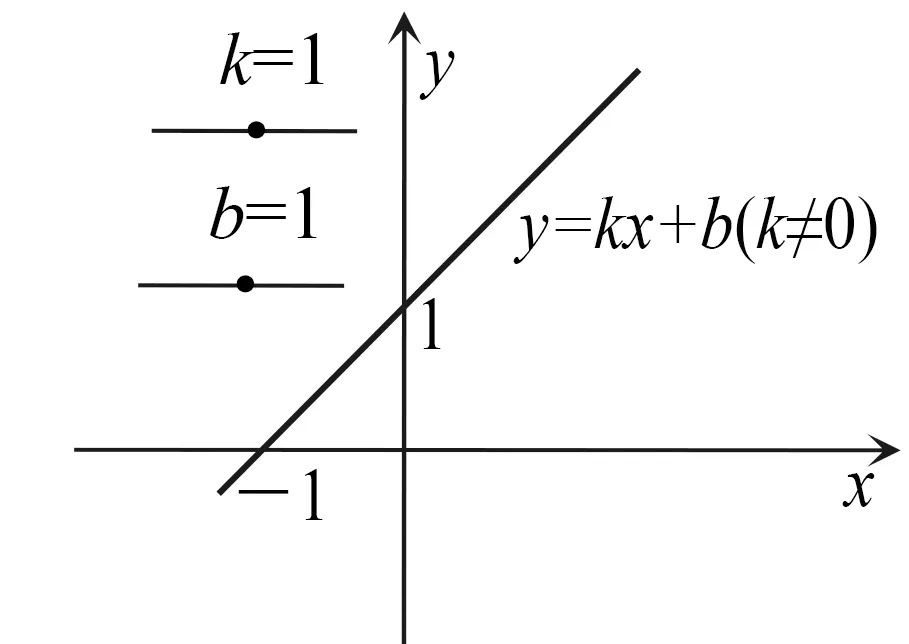
圖13

2.7 鞏固·內化

學生展示并總結：正比例函數一定過原點，作圖時另取一點即可.一次函數表達式中k和b不同，函數圖象不同.變化紛繁復雜，但不變的是它的形狀是一條直線.

設計意圖GeoGebra的滑動桿動態功能讓學生直觀“看”到圖象的變與不變，為學生提供課后思考的空間.

2.8 應用·生活

研究了任意實數為自變量的一次函數圖象后，回到初始問題：長寬關系的圖象是一條直線嗎？

設計意圖經歷實際問題數學化的探究后回到生活中，明確數學學習的意義，為后續一次函數解決實際問題作鋪墊.

2.9 小結·收獲

通過本節課的學習，你有什么收獲？

設計意圖以知識框架圖為載體，梳理數學學習中知識、方法、思想相輔相成的作用.

3 教后反思

《課標2022年版》讓教師更加清晰地認識到教好數學是落實核心素養的前提.本節課利用數學釘板實驗創設開放式情境，在“做”數學中讓學生經歷數學化的過程.通過信息技術融合突破抽象難點，讓學生理解學科知識本質，在深度學習的助推下發展深層思維，培養理性精神和創新能力，逐漸形成數學核心素養.

3.1 深度學習是理解知識的重要方式

學習是基于新舊知識的聯系將新知識整合到原有結構的過程.而深度學習“深”在系統結構里，“深”在教學規律里，“深”在人的精神境界里，“深”在人的心靈里，是一種有意義的知覺模式.[4]本課借助釘板和皮筋圍長方形，構建真實的數學情境，讓學生帶著原有的知識、方法、經驗主動操作、思考、感受，構建新的知識體系.開放式的情境給予學生大膽想、多角度思、充分交流的機會，在操作中提出問題、解決問題.若按常規讓學生通過作不同函數圖象來發現一次函數圖象是一條直線，只是淺層的體驗，學生經歷的是模仿和記憶.而深度教學助力學生深度學習，感受數學的魅力，激發學生的興趣和創造性思維.在強化作圖范式時，先由學生自主嘗試，再集體糾偏，歸納方法后繼續批判反思，得到兩點作圖法及點的恰當取法，讓學生充分感受知識的關聯和自然生長，做到以生為本、讓學引思.在達到預期教學效果的同時，讓學生體驗深度學習自主理性、批判理解、聯系整合、遷移運用的完整過程[6]，促進高層次思維和能力的發展，體現深度學習的意義，培養學科核心素養.

3.2 技術融合是深度學習的應然選擇

強調信息技術，將“說”和“寫”的功能延伸，使每一個命題清楚明確.先是清楚明確，然后才是深刻生動；才是追求遷移應用、智慧生成；才是創新發展、生命活力.[4]本課難點之一在于教師無法將抽象知識“一次函數的圖象是一條直線”直接“言傳”，學生又很難“意會”.所以在學習一次函數作圖的初期常常出現很多“腦洞大開”的奇圖.因此，借助信息技術的表征優勢，利用GeoGebra對一次函數圖象進行可視化呈現，實現抽象數學知識與生動現實之間的聯系通道.通過GeoGebra對坐標軸進行放大縮小演示一次函數圖象上點的加密過程，從有限個點拓展到無限個點，觀察其位置關系是“緊密地挨在一起”，而構成的圖形是直線，真正解決理解難關，為后續學習“反比例函數圖象是曲線而不是一系列折線”打下基礎.GeoGebra的操作直觀清晰，讓學生沉浸在探究過程中，自主感知探索目的、理解探索方法，讓思維進入一個密集、深入且長遠的深度學習中.能夠流暢歸納出研究函數圖象的一般方法，在深刻領悟中得到厚實的思維發展.技術融合的可視化呈現彌補了數學抽象給學生帶來的陌生感和迷茫感，讓學生能夠有“看透”數學的機會，為數學學習注入活力，構建起抽象與現實之間的橋梁，使本課核心知識生長在最恰當的時間.