基于改進擾動觀察法的光伏M PPT控制研究

張 杰 李良光

（安徽理工大學電氣與信息工程學院，安徽 淮南 232001）

0 引言

近些年來，隨著傳統能源日益短缺、環境問題形勢嚴峻，利用和開發新能源已經是各國的研究重點。在碳達峰、碳中和目標的推動下，大力發展太陽能發電成為必然[1]。太陽能作為優質的可再生能源，具有環保性、廣泛性和經濟性等優勢，市場潛力和開發前景巨大，已被應用到各個領域，發揮了良好的作用[2]。對于已知的光伏系統而言，其最大功率與外界環境息息相關，如太陽光照強度、環境溫度等[3]。因此，為獲得最大功率，引入最大功率的算法十分必要。當前，功率追蹤方法有很多，擾動觀察法和電導增量法是目前最常使用的兩種算法，另外還有很多人工智能算法應用于最大功率點的追蹤，例如粒子群優化算法、布谷鳥算法、神經網絡算法等，智能算法雖然搜索能力強，能在復雜的環境中尋找最大功率點，但其需要多次復雜的計算，而且自尋優時間過長[4]。

在諸多算法中，擾動觀察法需要的未知參數少，計算簡單方便，找尋最大功率點的效率較高，能夠更好地應用于光伏發電系統。傳統的擾動觀察往往采用固定步長進行擾動，系統輸出功率在最大功率點附近振蕩明顯，導致輸出不穩定，造成能量損失[5]。因此，本文采用變步長跟蹤擾動觀察法來改善速度與穩定性，提高太陽能轉化效率，減少光伏發電系統最大功率狀態運行下振蕩所帶來的能量損失，最后通過Matlab/Simulink進行仿真。

1 光伏電池的模型與特性

光伏電池是一個能量轉換裝置，它可以將太陽能通過電池內部的半導體結構直接轉換成可控且有規律的電能[6]。為了在光伏系統的設計中更好地分析光伏電池的特性，以及與光伏控制系統更好地適配，達到最佳發電效果，有必要建立光伏電池的數學模型，如圖1所示。圖中的二極管D模擬光伏電池PN結內電場的分流作用，分流之后的能量輸出到負載RL，光伏電池的內部損耗由并聯的電阻RP和串聯的電阻RS表示[7]。

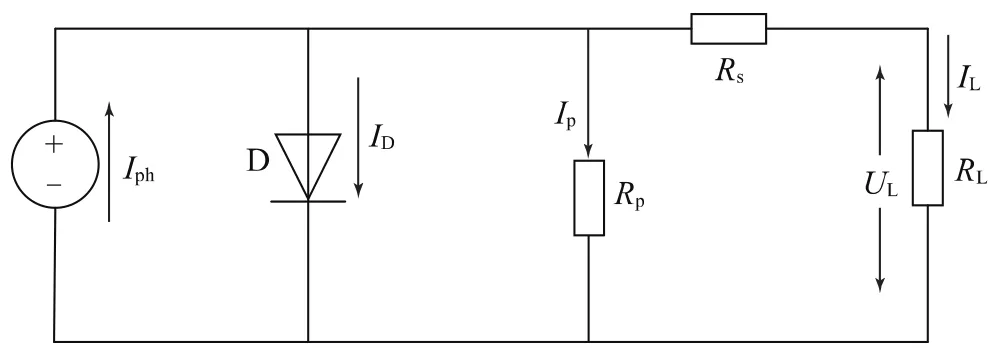
圖1 光伏電池等效電路模型

由圖1可知，根據KCL定律可得：

其中：

在圖1所示的光伏電池等效電路中，串聯電阻RS較小，并聯電阻RP較大且大于串聯電阻RS，對于理想光伏電池可忽略RP的影響，所以式（1）可簡化為：

式（3）中各個物理量含義如表1所示。

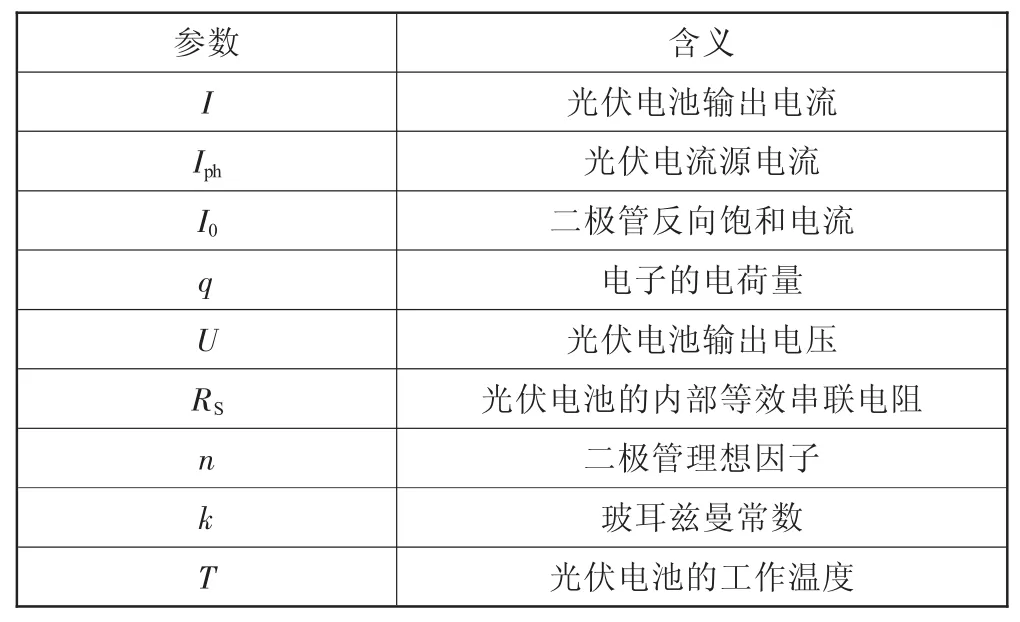
表1 光伏電池特性方程參數

2 光伏電池的輸出特性

在Matlab軟件中可知在溫度為25℃，光照強度為1 000 W/m2，Uoc=36.3 V，Isc=7.84 A，RS=0.39 Ω，根據以上參數可以確定光伏電池的輸出電壓與輸出電流的關系以及輸出功率與輸出電壓的關系。圖2為光伏電池I—U特性曲線，圖3為光伏電池P—U特性曲線，由圖2、圖3可知光伏電池輸出特性是非線性的，但其在運行過程中有唯一的最大功率點，所以，采用最大功率點追蹤方法來控制光伏電池的最大功率點，有利于提高光伏電池的發電效率。

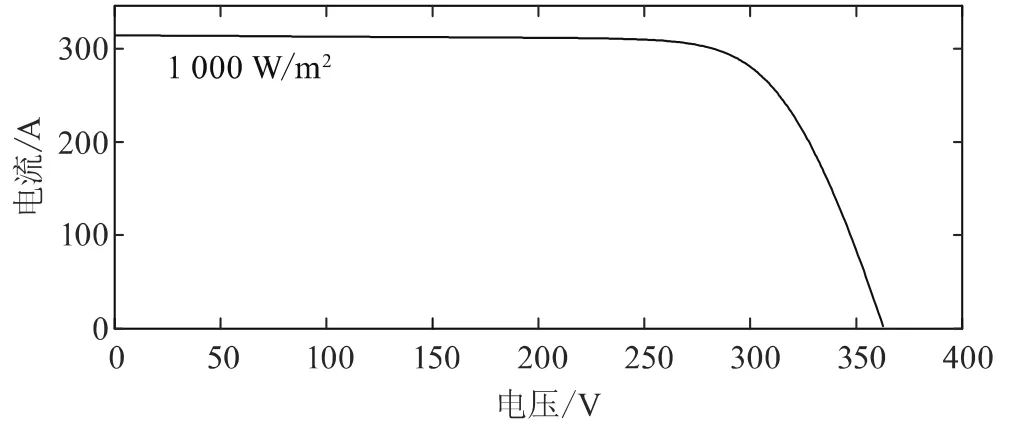
圖2 光伏電池I—U特性曲線

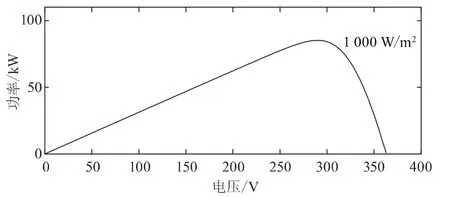
圖3 光伏電池P—U特性曲線

3 傳統擾動觀察法

傳統擾動觀察法，即在一定時間內對光伏電池的功率P和電壓V進行實時采樣，并給系統一個固定的擾動量ΔV，圖4為傳統擾動觀察法的流程圖，當ΔP/ΔV=0時即達到光伏電池的最大功率點；當ΔP/ΔV＞0時，說明此時工作點在最大功率點的左側，需要升高電壓；反之，ΔP/ΔV＜0時，說明此時工作點在最大功率點的右側，需要減小電壓。

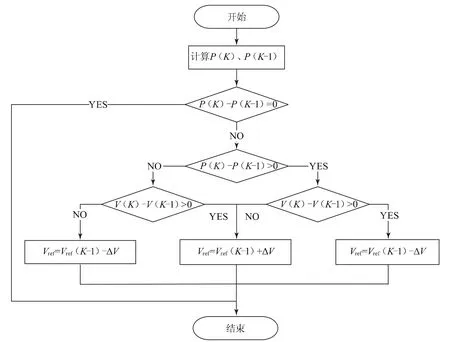
圖4 擾動觀察法流程圖

傳統擾動觀察法有控制簡單、容易實現等優點，但是，擾動步長的選取直接影響追蹤的效果，選取大步長時，追蹤速度快，但振蕩明顯，幅度較大；選取小步長時，振蕩幅度較小，但追蹤速度緩慢[8]。所以，步長的選取非常關鍵。

4 改進的擾動觀察法

傳統的擾動觀察法通常全程采取固定的擾動步長來保持追蹤最大功率點的運行狀態，無法同時兼顧追蹤速度和運行狀態的穩定性。本文提出的改進的擾動觀察法，采取非固定的擾動步長來兼顧最大功率點追蹤的速度與穩定性，具體是當光伏系統啟動時采取大步長進行擾動以提高最大功率點的追蹤速度，當臨近追蹤目標時采取小步長以減小系統振蕩幅度，提高系統的穩定性。由圖3可知，光伏電池P—U特性曲線的斜率不斷變化，即dP/dV在時刻變化，|dP/dV|值越小，系統的工作點越接近最大功率點；|dP/dV|值等于0，系統的工作點在最大功率點處。根據這一特性，將|dP/dV|作為步長的調整系數。取ΔV=α×β，α取值為0.1，圖5為改進的擾動觀察法的流程圖。

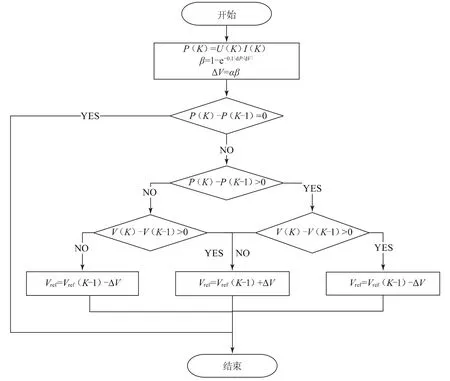
圖5 改進的擾動觀察法流程圖

5 仿真實驗及分析

采用Matlab/Simulink進行模型搭建以驗證改進的控制策略的可行性。將光伏電池分別接入編寫傳統擾動觀察法和改進的擾動觀察法的S-Function模塊中，采用PI調節器對系統的輸出電流進行精準控制，保證其穩定性。其中子系統是PWM模塊，是能夠按照一定規則調制各脈沖寬度進而改變占空比的脈寬調制器。系統在光照強度為1 000 W/m2、溫度為25℃的條件下運行0.5 s，最終得到兩種方法的輸出功率曲線圖，再進行對比分析。

圖6、圖7為傳統擾動觀察法與改進的擾動觀察法的輸出功率曲線圖，二者均在0.05 s左右達到最大功率點，但傳統擾動觀察法振蕩明顯，改進的控制策略在保證追蹤速度的同時大大提高了系統的穩定性，能夠兼顧光伏系統運行的速度與穩定性。

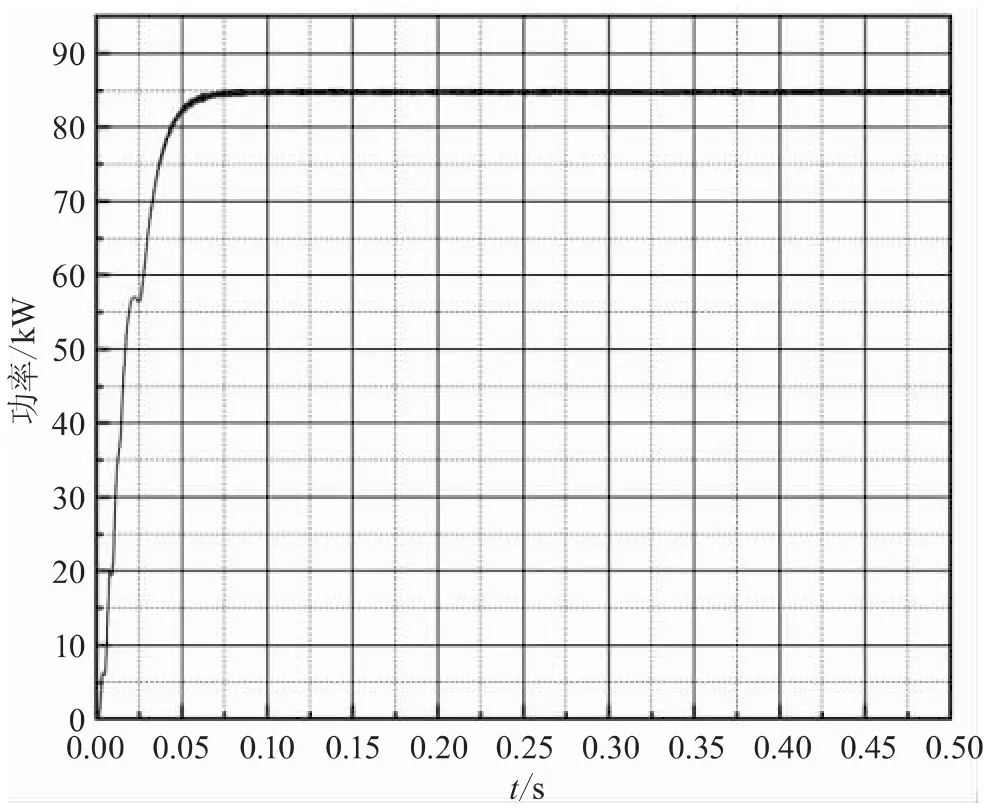
圖6 傳統擾動觀察法輸出功率曲線

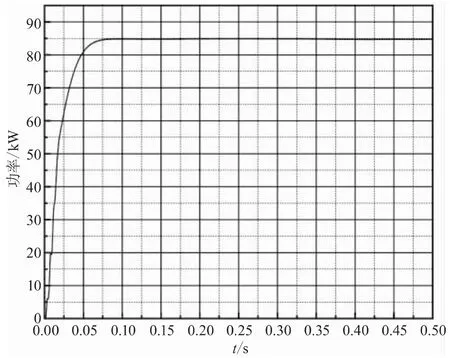
圖7 改進的擾動觀察法輸出功率曲線

另外，對傳統的擾動觀察法和改進的擾動觀察法的輸出功率曲線圖截取0.26～0.27 s、功率范圍為84.4～85.2 kW的部分進行對比，如圖8、圖9所示。從圖8中可以看出，當系統達到最大功率點時，傳統的擾動觀察振蕩很大，導致能量損耗嚴重；如圖9所示，改進的擾動觀察法顯著減小了振蕩幅度，避免了過多的能量損失。

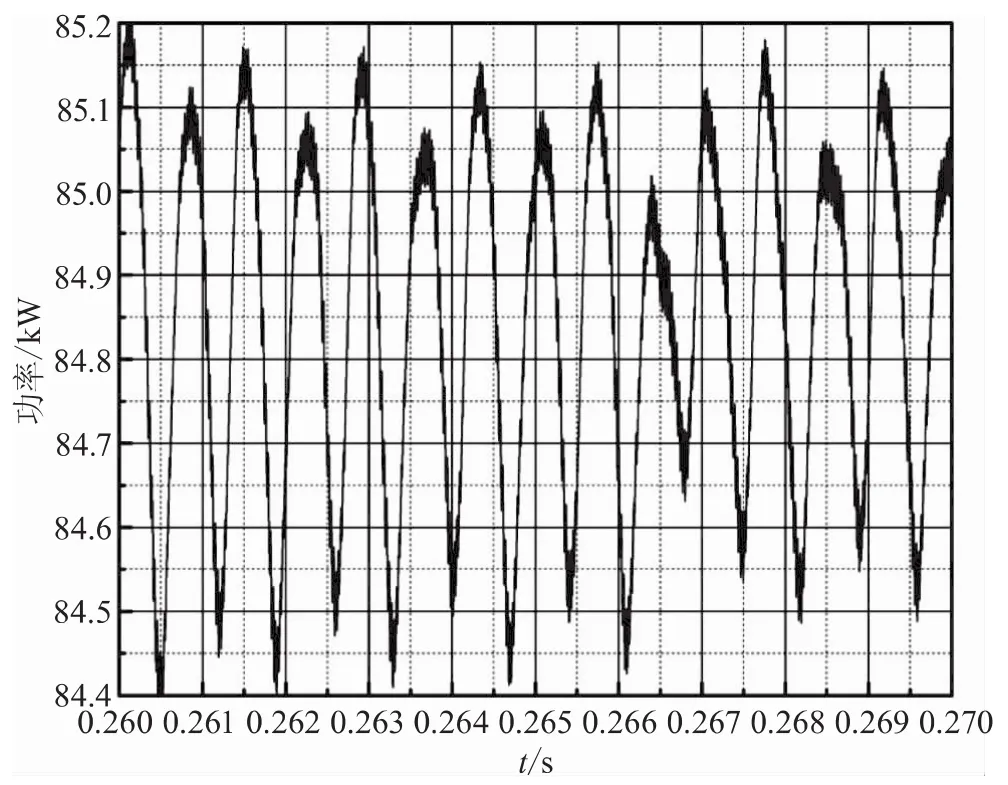
圖8 傳統擾動觀察法0.26～0.27 s的輸出功率曲線

圖9 改進的擾動觀察法0.26～0.27 s的輸出功率曲線

6 結論

本文針對傳統擾動觀察法的不足，提出了一種改進的擾動觀察法，在分析光伏電池的模型和輸出特性的基礎上，通過Matlab/Simulink進行建模與仿真，對仿真結果進行分析得出，本文提出的改進的擾動觀察法能夠兼顧追蹤速度和系統運行的穩定性，有效減少能量損失，提高發電量。