基于廣義憶阻器的超混沌系統的研究與電路實現

李新穎,盧毅

(蘭州交通大學 電子與信息工程學院,甘肅 蘭州 730070)

蔡少棠教授[1]首次依據電路對稱理論,闡述了電荷量與磁通之間還存在一種聯系,即憶阻器。在21 世紀初,惠普實驗室[2]成功研制出二端憶阻元件,證實了其物理的可實現性。憶阻器因存在非易失性和獨特的非線性特性[3-4],受到了研究者的廣泛關注。其在混沌電路、保密通信、憶阻神經突觸電路等領域的應用研究也獲得了很大的進展。

同時將憶阻器引入混沌系統后,可以得到憶阻混沌系統,比普通混沌系統具有更強的偽隨機性和復雜性以及多穩定特性,可以使系統切換狀態來維持穩定,在信息保密與隨機信號發生器方面有理論意義與實際工程應用價值。包伯成等[5]通過將蔡氏電路二極管替換為憶阻器,設計出憶阻器電路,所得系統的穩定性取決于憶阻器的初始狀態,且有線平衡點。孫克輝等[6]用二次型磁控憶阻器作為反饋項,加入Lorenz 系統后,得到一個新型四階超混沌系統。俞清等[7]基于廣義憶阻器,搭建了憶阻混沌電路,并對其共存分岔模式進行分析。Teng 等[8]利用四次多項式函數構造了一個新的憶阻器模型,與一般模型不同,該憶阻器模型具有兩個最小值和一個最大值。Bao 等[9]提出了一個基于憶阻器的Jerk 系統,該系統存在4 個線平衡和無限多吸引子共存的超級多穩態現象。通過在混沌系統引入憶阻器反饋或用憶阻器替換混沌系統中的非線性項,是目前構建憶阻混沌系統的兩種方式。構建不同類型的維度更高、混沌性更強的憶阻混沌電路,以及探究憶阻混沌電路中更多復雜的動力學特性,可以為混沌電路的應用奠定基礎,為信息保密與隨機信號發生器方面提供系統支持。

為拓展憶阻器模型,構建復雜性更高的混沌系統以及探究憶阻混沌系統的各類特性,并得到有更多復雜動力學行為的憶阻器混沌電路,本文基于一個三維非線性混沌系統,加入新設計的廣義磁控憶阻器模型,設計出新型憶阻混沌系統,并搭建了模擬電路。分析了憶阻混沌系統的李雅普諾夫指數、耗散性、平衡點集、穩定性、相圖等動力學特性以及部分特殊的混沌特性,如分岔特性、多吸引子共存等,發現新構建憶阻混沌系統有更強的混沌性與復雜性。新系統拓展了高維混沌系統類型,同時符合混沌電路、保密通信等領域的要求,滿足科研中對復雜不可預測混沌系統的需求,實現憶阻器在混沌電路領域的應用研究。最后通過系統模擬設計與電路仿真的相圖等相互驗證,表明系統可用于實際的生產生活中。

1 基于廣義憶阻器的新型混沌系統設計

1.1 廣義憶阻器模型

Chua 提出廣義憶阻器通用模型如式(1)所示[10]:

式中:v(t)和u(t)代表廣義憶阻器的輸出量與輸入量;x為廣義憶阻器的內部狀態變量;函數G是連續的n維向量函數;函數H是連續的標量函數。本文基于通用模型設計出一種電壓控制的廣義憶阻器模型[11],該廣義磁控憶阻器模型的公式描述如下:

式中:a=0.1,b=20,c=d=0.1。

該廣義磁控憶阻器模型的電壓、電流關系如圖1 所示。圖1(a)為固定激勵幅度,不同頻率下的I-V曲線;圖1(b)為固定激勵頻率,不同幅度下的I-V曲線。由圖1 可知,該模型的電壓、電流關系為斜類“8” 字型的緊磁滯回線,滿足憶阻器電壓和電流的關系特性[12]。

給定輸入電壓v=Vsin(2πft),如圖1(a)所示當固定激勵電壓幅度V=10 V,頻率分別為5,20,40 Hz時,磁滯回線的旁瓣面積隨著激勵頻率的增大而減小。當激勵頻率增大到一定值時,緊磁滯回線將呈現一條直線。當固定輸入頻率f=5 Hz 時,電壓分別取V=4,7,10 V 時,由圖1(b)可以發現磁滯回線的旁瓣面積隨著激勵電壓幅度V的增大而增大。則此廣義憶阻器模型符合憶阻元件的三個本質特征[13]。

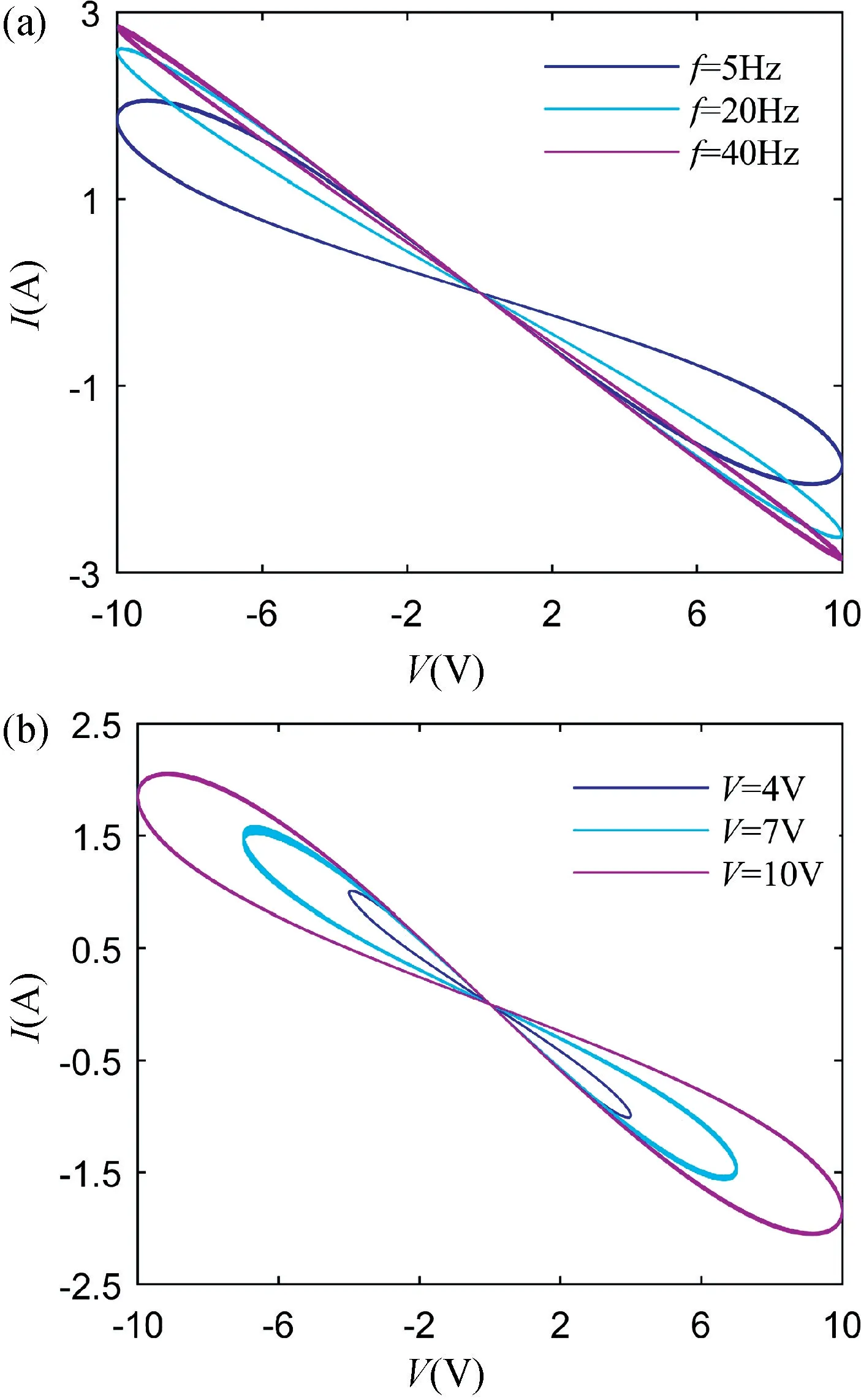
圖1 不同頻率與幅度時的I-V 曲線。(a) f=5,20,40 Hz 時的I-V 曲線;(b)V=4,7,10 V 時的I-V 曲線Fig.1 I-V curves at different frequencies and amplitudes.(a) I-V curves at f=5 Hz,20 Hz,40 Hz;(b) I-V curves at V=4 V,7 V,10 V

1.2 一種新的基于非線性憶阻模型的混沌系統

給出三維Sprott-B 混沌系統,其無量綱狀態方程為[14]:

式中:a,b,c是混沌系統的常數型參數。在這里,使流經憶阻器的磁通表示為第四個狀態變量w,狀態變量y則為憶阻器兩端的電壓,作為反饋引入到混沌系統中,并在狀態z中加入憶阻項,增強憶阻特性,再調整參數,得到由憶阻器組成的四階憶阻超混沌系統,混沌系統模型如下:

其中

取α=0.1,β=20 構成新型憶阻超混沌系統。x,y,z,w是狀態變量,增益系數k=0.1,而a=3,b=15,c=30,d=e=0.01 是新的基于憶阻器的混沌系統參數,系統存在典型的混沌吸引子。代入參數后混沌系統如式(6)所示:

1.3 憶阻混沌系統的相圖

在式(6)基礎上,利用Matlab 對新型混沌系統進行數值仿真,取混沌系統初值x=y=z=w=0.1,得到新型憶阻混沌系統的吸引子。圖2(a)～(d)分別是憶阻混沌系統在x-y、x-z、y-z、y-w平面的相圖。由圖2 可知新系統存在混沌現象,有著奇異吸引子。

圖2 新型憶阻混沌系統的相圖。(a)x-y 相圖;(b)x-z 相圖;(c)y-z 相圖;(d)y-w 相圖Fig.2 Phase diagram of a new memristor chaotic system.(a) x-y phase diagram;(b) x-z phase diagram;(c) y-z phase diagram;(d) y-w phase diagram

2 新型混沌系統的散度、平衡點、李雅普諾夫指數值及分岔圖

2.1 散度

對于一個新型系統要產生混沌現象,這就要求系統散度要小于或等于零。其中系統散度等于零,說明該系統的體積不變,系統是有界限的。當系統的散度小于零時,系統是耗散系統,系統體積收縮。四階系統的李氏指數有兩個大于零時,系統的相軌跡會產生拉伸,此時若系統是有界限的,必然產生折疊運動。系統體積收縮與相軌跡拉伸相互作用的結果,便是產生混沌運動。

結合式(6),該新型混沌系統的散度計算如式(7)所示:

散度小于零,即該系統是耗散的。

2.2 平衡點與穩定性

為求出式(6)平衡點,令式(6)左邊等于0,即:

由式(8)可得平衡點O={x,y,z,w|x=y=0,z=α,w=-30},α可為任意常數,可推導出式(6)存在線平衡,有無盡的平衡點集。

由此,式(6)的雅可比矩陣為式(9):

因此該雅可比矩陣J0的特征方程為:

解得λ1=0,λ2=0。

由式(11)和(12)可知,當α＞-18301.25 時,特征值λ3和λ4均為實數,此時系統平衡點是穩定的;當α＜-18301.25 時,特征值λ3和λ4均為復數,此時,系統的平衡點是不穩定狀態。

2.3 李雅普諾夫指數

取混沌系統狀態初值x=y=z=w=0.1,計算得出該系統李雅普諾夫指數值為LE1=1.0812,LE2=0.0045,LE3=-0.0093,LE4=-16.3307,有兩個正值且系統指數之和小于零,所以該系統為超混沌系統。

2.4 混沌系統的分岔圖

由于初始混沌系統引入了憶阻器反饋項,原本的混沌系統將會更加復雜以及出現不同的行為特性,因此分析了其參數變化對系統的影響。令式(4)參數a在(2,3)的范圍時觀察系統分岔特性,如圖3 所示。從圖3(a)可以看出系統由單周期態出發經過倍周期分岔進入二周期狀態,再經過倍周期分岔逐漸進入混沌狀態。同時,圖3(b)中李雅普諾夫指數最大值從0 逐漸變化為正,也反映了系統從周期態到混沌態的變化過程,通過兩圖的對比可以很好地驗證該過程的一致性,得出系統隨參數a的變化存在著不同狀態,即系統存在隨著參數變化的多穩態特性。

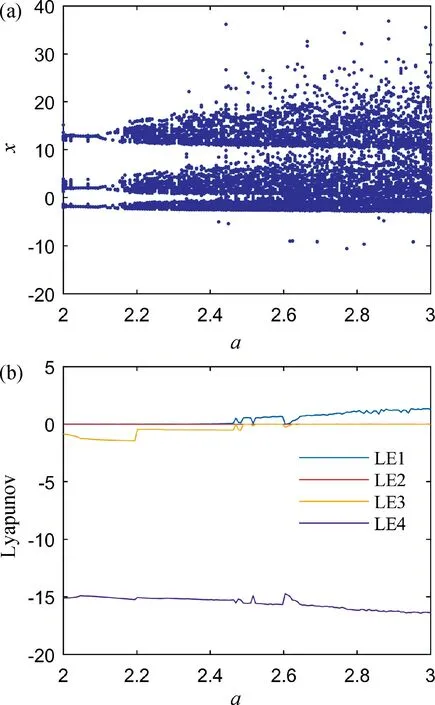
圖3 分岔圖與李雅普諾夫指數圖。(a) a∈(2,3)的分岔圖;(b) a∈(2,3)的李雅普諾夫指數圖Fig.3 Bifurcation diagram and Lyapunov exponent diagram.(a) Bifurcation diagram with a ∈(2,3);(b) Lyapunov exponent diagram with a ∈(2,3)

2.5 多吸引子共存現象

混沌系統加入憶阻器反饋項后,往往會出現憶阻器初值影響混沌系統狀態的現象,當出現不同憶阻器初值對應不同混沌吸引子狀態時,稱之為多吸引子共存現象[15-16]。固定式(6)混沌系統參數,將憶阻器初始值w(0)作為分岔參數,當w(0)在[-1.5,1]之間變化時,得到如圖4 所示分岔圖和李雅普諾夫指數圖。由圖4(a)與圖4(b)可知,w(0)在[-1.5,-1.15]之間,最大李雅普諾夫指數值在0 與正值之間變化,因此系統處于混沌與周期交替的狀態;w(0)在(-1.15,-0.658] 之間,最大李雅普諾夫指數值為0,系統處于周期狀態;w(0)在(-0.658,1]之間,最大李雅普諾夫指數值為正,系統處于混沌狀態。初值w(0)在[-1.5,1]范圍內,取w(0)=-1 時作吸引子相圖,如圖5(a)所示,為周期態;取w(0)=0 時作吸引子相圖,如圖5(b)所示,為混沌態。可見系統在不同憶阻器初值時,系統的狀態隨初始值的變化而變化,即憶阻器初值的不同會使憶阻混沌系統存在多種不同的吸引子,導致多穩態特性的出現。

圖4 隨初始值w(0)變化的分岔圖與Lyapunov 指數圖。(a) w(0)∈[-1.5,1] 的分岔圖;(b) w(0)∈[-1.5,1]的Lyapunov 指數圖Fig.4 Bifurcation diagram and Lyapunov exponent diagram with initial value w(0).(a) Bifurcation diagram with w(0)∈[-1.5,1];(b) Lyapunov exponent diagram with w(0)∈[-1.5,1]

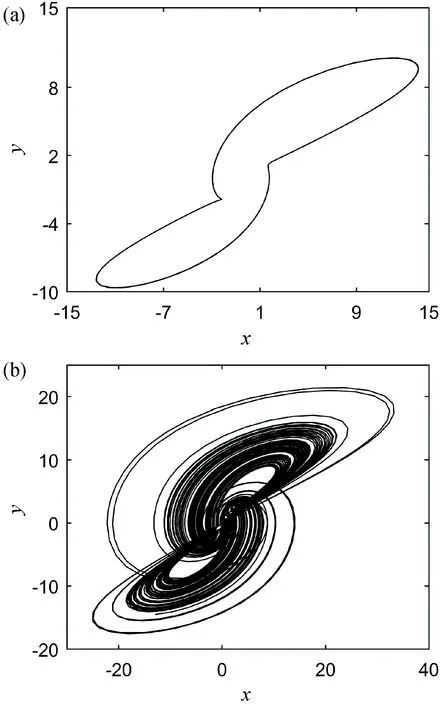
圖5 不同w(0)下的吸引子相圖。(a)w(0)=-1 時的x-y 相圖;(b)w(0)=0 時的x-y 相圖Fig.5 Attractor phase diagram under different w(0).(a) x-y phase diagram when w(0)=-1;(b) x-y phase diagram when w(0)=0

3 新型混沌系統的電路設計

為使該憶阻混沌系統在實際工程應用中有價值,設計了相應的混沌憶阻電路,并通過示波器觀察形成的相圖。混沌電路設計主要由兩部分組成: 第一部分通過新型混沌系統的狀態方程,設計相應的電路模塊;第二部分是將電路模塊進行組合,形成混沌系統電路。通過對混沌系統電路的相圖與數值模擬的結果做對比,驗證混沌系統的可行性[17-19]。電路通過分模塊來實現x,y,z,w四個狀態量,采用TL074CN 型號的運算放大器Ui(i=1,2,…,7)和電容來實現反向積分功能,用AD633 型號、乘法因子為0.1 的乘法器實現非線性部分以及聯立線性電阻、電容搭建電路。為使狀態變量范圍在±13 V 內,對狀態變量進行壓縮變換,即使x=10x,y=5y,z=5z,w=w再進行尺度變換,令時間常數τ0=100,得式(13):

式(13)對應的電路的狀態方程為:

設電路中的電容C1=C2=C3=C4=100 nF,R1=R2=R5=R6=R11=R12=2 kΩ,R3=R7=R13=1 kΩ,R4=1.333 kΩ,R8=3.333 kΩ,R9=6.662 kΩ,R10=0.5 kΩ,R14=1 kΩ,R15=100 kΩ,R16=500 kΩ,R17=2000 kΩ,R18=200 kΩ,v1=6 V,VEE=-13 V,VCC=13 V,構建圖6 所示憶阻混沌電路,其中圖6(a)為系統x,y狀態量的電路構造,圖6(b)為系統z,w狀態量的電路構造。

圖6 超混沌系統電路實現。(a)x, y 狀態量的電路結構;(b)z, w 狀態量的電路結構Fig.6 Circuit realization of hyperchaotic system.(a) Circuit structure of x and y state quantities;(b) Circuit structure of z and w state quantities

運行電路仿真,則從圖7 示波器顯示相圖中可以看出,混沌電路有著混沌吸引子,相軌跡難以預測。通過將混沌電路的結果與Matlab 仿真結果相比較,兩者相運動軌跡基本一致,由此驗證了混沌電路與仿真結果的一致性以及混沌電路的可實現性,確保系統可用于實際的生產生活中。

圖7 示波器混沌吸引子。(a)x-y 相圖;(b)x-z 相圖;(c)y-z 相圖;(d)y-w 相圖Fig.7 Chaotic attractor of oscilloscope.(a) x-y phase diagram;(b) x-z phase diagram;(c) y-z phase diagram;(d) y-w phase diagram

4 結論

本文基于通用憶阻器模型,設計了一個廣義憶阻器,并將其引入Sprott-B 混沌系統,構建了一個新的憶阻超混沌系統,并搭建了憶阻混沌電路。通過對憶阻混沌系統包括相圖、李雅普諾夫指數、耗散性、平衡點集、穩定性、參數分岔、多穩態等特性的分析,發現新構四階憶阻混沌系統為超混沌系統,存在線平衡點和多吸引子共存現象,標志著其更強的復雜性與混沌性,符合對更強的偽隨機性、復雜性以及多穩定特性系統的要求,則此新構系統可通過切換狀態實現信息保密與隨機信號發生器方面的應用。其次,憶阻混沌電路的構建驗證了系統的可行性與一致性。類似Bao 等在混沌系統引入二次項反饋的結果,引入廣義憶阻器的混沌系統有隨參數變化的分岔特性和多吸引子共存等新動力學行為,實現了對包含廣義憶阻器的超混沌系統形成過程的研究,并為憶阻器模型以及憶阻混沌電路領域的應用提供了一定依據,同時在圖像加密、保密通信等領域有一定應用價值。