脈沖用金屬化膜電容器穩態熱分析研究

邱昊,高秀華,邱林俊,王勇平

(成都宏明電子股份有限公司,四川 成都 610000)

金屬化膜是利用高真空蒸鍍技術,在有機薄膜(如聚丙烯、聚酯等)表面蒸鍍一層鋁、鋅和鋅鋁復合金屬薄層而成,其特點是金屬層厚度薄。以厚度為納米級的導電金屬層作為電容器電極,為電容器小型化提供新的思路。金屬化膜電容器具有儲能密度高、可靠性高、壽命長和損耗小等特點,是脈沖功率系統中常用的儲能元器件,常用于微波、激光、粒子加速器、電磁武器、醫療器械、勘探和環保領域等。

目前脈沖用金屬化膜電容器一般采用聚丙烯薄膜作為介質,蒸鍍電極材料為鋅鋁復合材料。由于金屬電極很薄,金屬化膜方阻較大,在連續長期工作下電容器發熱是一個重要問題,會導致電容器工作失效,甚至燃燒、爆炸等故障。

李化等[1]提出在金屬化膜電容器溫升模型中,等效串聯電阻(ESR)在脈沖放電結束后產生熱量由金屬電極向有機薄膜徑向傳導,并且軸向往端面傳導;范麗娜等[2]提出電容器外表溫度和電容器芯子最熱點的關系,對預測電容器使用壽命非常有價值;徐夢蕾等[2]提出膜塊寬度與熔絲寬度比、環境溫度對電容器最高溫度的影響,推導出各影響因素與最高溫度的對應關系。

因此,從脈沖用電容器運行穩定性、金屬化膜耐壓性能和電容器壽命等方面考慮,有必要對電容器穩態運行進行熱分析,開展電容器散熱優化設計。本文采用有限元仿真軟件,依據電容器零部件尺寸和裝配條件建立模型,通過仿真計算結果和試驗結果對比,驗證了仿真模型的準確性。最后,通過芯子卷繞參數和電容器工作周期理論計算,進行電容器優化設計,降低了電容器穩態運行內部溫度,提高了電容器運行的穩定性和安全性。

1 金屬化膜電容器發熱理論

金屬化膜電容器主要發熱源有: (1)有機薄膜介質損耗發熱;(2)金屬電極發熱;(3)端面接觸不良發熱[4-7]。李智威等[8]提出金屬化膜電容器在脈沖工作模式下,高方阻金屬電極發熱大于薄膜的介質損耗發熱,額定工況下電容器端面接觸發熱可以忽略不計,電極電阻發熱是主要的發熱來源。

1.1 等效電阻計算

在額定工況下,金屬電極總發熱功率近似等于電容器極板損耗功率[9]。

式中:Im為電流有效值;ESR 為電容器等效串聯電阻。金屬化膜結構見圖1。電容器容量C為28 μF。

圖1 金屬化膜結構圖Fig.1 Structure diagram of metallized film

由P=P損耗,可得:

式中:L為極板有效長度;b為有效寬度: 90 mm;Δb為卷繞留邊: 4 mm;Δb＇為卷繞錯邊: 1 mm;為金屬化膜方阻: 160 Ω;r＇為電容器接觸電阻和電極電阻。通過式(2) 計算可得等效串聯電阻ESR 為0.16 Ω。

1.2 電容器工作周期

一般脈沖功率系統按工作方式可分為兩類: 一是連續工作模式,以重復頻率長時間持續工作;二是爆發工作模式,以重復頻率連續工作時間t1后,間隔時間ti,按照t1+Tr規律長時間工作。脈沖功率系統重復頻率工作時,電容器、開關等關鍵器件溫升較大。單次電容器工作周期可分為: 充電階段、保壓階段、放電階段和間隔階段[8]。

電容器工作周期見圖2。其中,tc: 充電階段時間,th: 保壓階段時間,td: 放電階段時間,ti: 間隔時間,Tr: 電容器工作周期。

圖2 電容器工作周期Fig.2 Working period of capacitor

1.3 發熱功率計算

電容器長期運行,通過討論其高重復頻率工作的發熱功率為電容器熱分析提供依據。電容器典型放電回路見圖3。其中,電容器雜散電感ESL: 0.2 nH,負載R: 2.4 Ω。

圖3 電容器典型放電回路圖Fig.3 Typical discharge circuit of capacitor diagram

單次脈沖金屬化電容器充放電回路總功率為:

單次脈沖金屬化膜電容器發熱功率為:

2 金屬化膜熱傳導理論

依靠構成物質的粒子,如原子、分子、自由電子,從物體較熱區域向較冷區域提供的能量稱為熱。熱傳導是一種特定方式的傳熱,這種傳熱方式的能量交換發生在固定或靜止流體內,依靠物體內部的溫度梯度從高溫區域向低溫區域傳輸能量[11]。

2.1 金屬化膜電容器熱傳導過程

金屬化膜電容器由金屬化膜卷繞而成,每層金屬電極都會發熱向相鄰有機薄膜傳導。在仿真計算中,將卷繞的電容器芯子看成均一的介質[12]。金屬化膜電容器熱傳導過程見圖4。

圖4 電容器熱傳導過程圖Fig.4 Heat conduction process diagram of capacitor

2.2 金屬化膜電容器芯子各向異性

在各向同性的固體中的熱傳導,各向同性材料的導熱系數與方向無關,所以導熱系數無需考慮方向問題。由于金屬化膜是在有機薄膜表面真空蒸鍍一層金屬電極復合材料,因此研究金屬化膜電容器內部熱傳導需要考慮金屬化膜材料的各向異性。金屬化鋅鋁膜最大優點是容量損失小、抗氧化性強、鍍層與有機薄膜附著力強[14]。電容器在工作過程中,自愈面積與自愈持續時間隨著自愈能量的增加而增加,自愈能量與電壓二次方成正比、與方阻的二次方成反比,采用高方阻金屬化膜可有效降低容量損失,提高電容器壽命[15]。因此脈沖用電容器一般采用鋅鋁復合高方阻金屬化膜。金屬化膜電容器芯子展開圖見圖5。

圖5 金屬化膜電容器芯子展開圖Fig.5 Expanded diagram of the core of metallized film capacitor

在電容器內部,熱量沿電容器芯子軸向和徑向進行熱傳導。沿軸向等效熱導率為:

式中:dm為金屬電極厚度;dp為有機薄膜厚度;λm為金屬導熱系數;λp為有機薄膜導熱系數。

當熱量沿芯子徑向傳導時,則徑向等效熱導率為:

金屬化膜電容器芯子傳熱微元見圖6。通過式(5)和式(6)計算可得芯子在三維坐標系下各向異性導熱系數。X,Y,Z軸導熱系數分別為: 0.22,0.22,0.226 ℃/W。

圖6 芯子傳熱微元Fig.6 Heat conduction micro element of core

2.3 金屬化膜電容器散熱

電容器散熱方式主要有對流散熱、輻射散熱和傳導散熱[14]。處于無限大空間中時電容器各個表面對環境的散熱表現為自然對流散熱。電容器在空氣自然對流散熱計算公式見式(7)。

式中:λ為空氣導熱系數;L為傳熱面特征長度;Nu為Nusselt 數。本文研究的是在無限大空間中,恒熱流電容器進行自然對流散熱。對流散熱系數一般與物體形狀、環境特性等因素有關。

對于恒熱流豎直平壁散熱表面Nusselt 數為:

對于恒熱流水平散熱表面,分熱面向上(冷面向下)和熱面向下(冷面向上),對應Nusselt 數為:

式中:Gr為Grashof 系數,表示流體的浮生力和粘性力的相對大小;Pr為空氣普朗特數。格魯曉夫Gr計算公式為:

式中:αv為空氣膨脹系數;Tw為物體表面溫度;T0為環境溫度;g為重力加速度;v為運動粘度。

假設空氣為理想氣體,空氣膨脹系數為:

本文綜合散熱系數h通過式(7)計算可知為6.8 W/(m· ℃),其中Pr、v和λ可以通過文獻[14]查詢。

3 金屬化膜電容器理論模型與仿真

有限元法(Finite Element Method)是一種將連續體視為若干個有限大小的單元體的離散化集合,以求解連續體熱、力、電磁問題的數值方法,其基本思想是將連續的求解區域離散為一組有限個、且按一定方式相互連接在一起的單元的組合體[15]。

3.1 模型搭建

利用SolidWorks 軟件對金屬化膜電容器按照零部件尺寸和裝配條件進行建模。電容器模型包含: 芯子、噴金層、環氧樹脂、引出電極和PPS 外殼[16]。根據電容器結構特點和本文研究內容對電容器仿真模型作以下簡化和假設:

(1)由于電容器內部結構復雜,忽略引出電極和焊點的影響,電容器芯子作為均勻發熱源;

(2)將電容器內部有機薄膜及鋅鋁金屬層等效為一種材質,考慮在三維坐標系下電容器芯子沿其軸向和徑向熱傳導;

(3)忽略電容器芯子內部空間間隙;

(4)電容器芯子端面施加噴金層,電容器內部除零部件之外全部填充環氧樹脂。

3.2 建模結果分析

在SolidWorks 中建立金屬化膜電容器三維仿真模型,電容器由內到外包含: 1 根芯棒,1 個芯子,芯子與外殼之間填充聚氨酯,1 個外殼。電容器仿真模型見圖7。

圖7 電容器仿真模型Fig.7 The simulation model of capacitor

3.3 材料屬性定義

利用SolidWorks 軟件對電容器進行穩態熱分析時,需要對材料的導熱系數、比熱容和質量密度進行定義。芯子各向異性的導熱系數已知,其余材料通過查閱資料得到電容器材料屬性參數見表1 所示[14]。

表1 電容器材料屬性參數Tab.1 Material propertie sparameters of capacitor

3.4 網格劃分

有限元網格劃分結果直接關系仿真時間長短和計算結果準確性[15]。有限元網格劃分一般分為自由網格劃分、掃描網格劃分、映射網格劃分。自由網格劃分對于單位形狀沒有嚴格限制和要求;網格劃分粗細直接影響仿真時間長短和仿真計算結果,伴隨著網格密度增加,計算精度隨之提高,同時增加了計算時間。然而網絡密度到達一定程度后,計算精度增加較少,計算時間卻增加較多。由于文中研究的電容器體積小,內部填充聚氨酯形狀不規則,所以綜合考慮采用自由網格劃分,標準網格大小為(2.8±0.14) mm,網格品質高,雅克比點: 16,計算時間: 5 s。電容器有限元自由網格劃分模型見圖8。

圖8 電容器仿真模型網格劃分Fig.8 The meshing of simulation model capacitor

3.5 仿真參數

電容器連續運行中,保壓階段是電容器不斷自愈的過程,內部局部自愈產生的熱量會帶來溫升[17]。因此為了研究電容器長期運行內部穩態溫度,忽略保壓階段內部局部自愈溫升的影響,電容器工作周期見圖2 所示。

仿真模型邊界條件和熱載荷參數:T0是環境溫度:17 ℃,h是綜合散熱系數: 6.8 W/(m· ℃),U是工作電壓: 4 kV,C是電容容量: 28 μF,Ts是工作周期: 8.006 s,P0是施加的熱載荷: 1.75 W。電容器內部設置溫度傳感器位置見圖9。

圖9 電容器溫度傳感器分布圖Fig.9 Temperaturesensor distribution diagram of capacitor

4 仿真和試驗結果與討論

為了驗證仿真模型準確性,試制2 臺電容器,對金屬化膜電容器進行充放電試驗,測量其內部不同位置溫度,通過對比試驗和仿真結果,驗證仿真模型準確性。為了節約時間成本,假定溫度增長不高于0.5℃/100 次時,電容器內部達到穩定狀態。電容器實物圖見圖10。

圖10 電容器試驗實物圖Fig.10 Physical diagram of capacitor

電容器試驗參數:T1為環境溫度: 16.9 ℃,h為綜合散熱系數: 6.8 W/(m· ℃),C為電容器容量: 28 μF,U1為額定電壓: 4 kV,Tr1為單次充放電時間: 8 s。

4.1 仿真結果及分析

保持環境溫度和綜合散熱條件不變,對電容器施加熱載荷模擬其放電產生熱量,電容器高重復頻率工作后內部溫度達到穩態,電容器工作穩態溫度分布圖見圖11。可見,電容器芯子中心靠近芯管處溫度最高,位置2 溫度高于位置3 溫度,位置1 溫度高于位置3 溫度。

圖11 電容器脈沖工作溫度分布圖Fig.11 Distribution temperature chart of capacitor in pulse condition

4.2 試驗結果及分析

為了進一步研究電容器實際運行過程中內部溫度分布情況,在電容器內部預埋熱電偶,位置分別在芯子中心位置、芯子噴金上端面和芯子外包膜。本文以電容器1 次充放電試驗時間和間隔時間為電容器1 次脈沖工作周期。對#1、#2 電容器進行高頻次脈沖工作試驗,#1、#2 電容器脈沖工作后對電容器內部熱電偶進行采樣數據見表2、圖12 和圖13,試驗與仿真結果對比見表3。

圖13 #2 電容器脈沖工作溫度分布趨勢圖Fig.13 Test temperature distribution trend of #2 capacitor in pulse condition

表3 試驗與仿真穩態溫度對比Tab.3 Comparison of test and simulation steady-state temperature

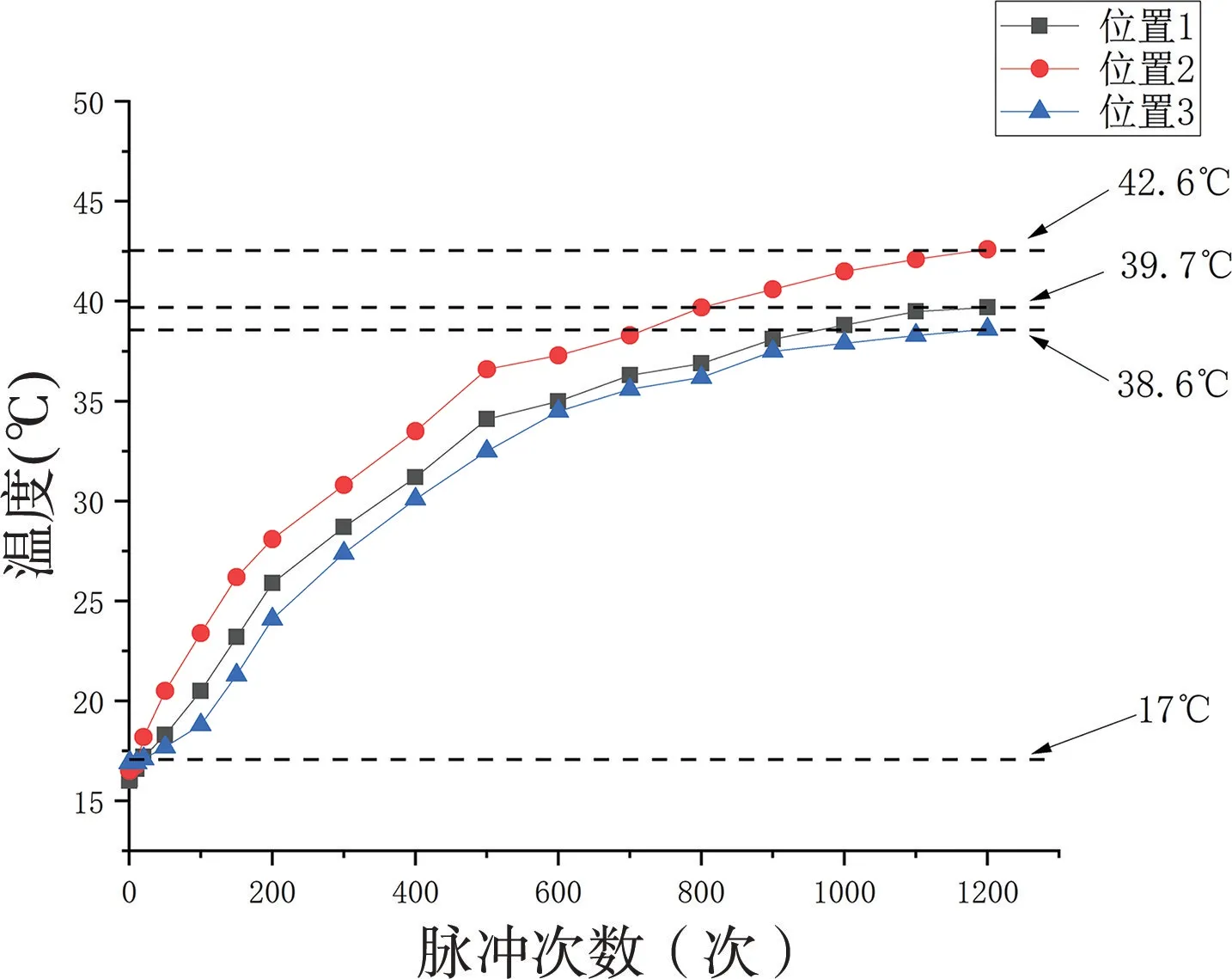
圖12 #1 電容器脈沖工作溫度分布趨勢圖Fig.12 Test temperature distribution trend of #1 capacitor in pulse condition

表2 電容器脈沖工作試驗數據Tab.2 Test data of capacitor in pulse condition

由表3 可知,仿真與試驗結果吻合度高,仿真模型可以較好地反映電容器內部穩態溫度。

5 電容器優化設計

電容器實際工作過程中,考慮到惡劣環境因素、系統超負荷運轉的影響,有必要對電容進行優化設計,降低電容器運行的穩態溫度[18]。假設電容器容量、額定電壓和介質耐壓強度一致,環境溫度: 17℃,綜合散熱系數: 6.8 W/(m· ℃),施加熱載荷: 1.75 W。

5.1 金屬化膜厚和膜寬的選擇

電容器的容量相同、工作電壓相同和介質耐壓強度相同是選擇金屬化膜厚和膜寬的前提條件。

單個電容器芯子金屬電極發熱功率P發熱為:

式中:ρ為金屬化膜電阻率;d為金屬化膜厚度。

n個電容芯子金屬電極Pn發熱發熱功率為:

由式(13)可知,電容器電極發熱與膜厚成反比,較大膜厚電容器的發熱功率較小,電容器整體內部溫升更小。

保持金屬化膜膜寬一致,改變膜厚建立芯子模型導入電容器模型;保持膜厚一致,改變膜寬建立芯子模型導入電容器模型。其熱分析結果見表4 和表5。

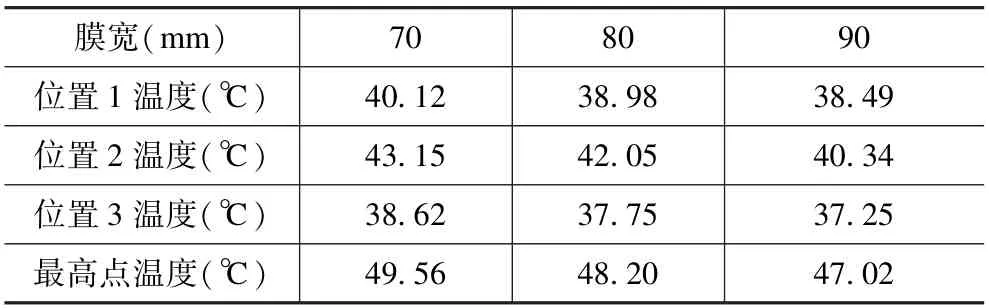
表5 不同膜寬電容器仿真穩態溫度Tab.5 Comparison of steady-state temperature simulation of capacitors with different film widths

由表4 可知,膜寬一致時,增加膜厚會降低電容器內部溫度。

表4 不同膜厚電容器仿真穩態溫度Tab.4 Comparison of steady-state temperature simulation of capacitors with different film thicknesses

由表5 可知,膜厚一致時,增加膜寬會降低電容器內部溫度。為了降低電容器運行時溫度,本文樣品最優設計方案為: 膜厚為8 μm 和膜寬90 mm 的卷繞參數設計方案。

5.2 電容器工作周期的選擇

一般脈沖電容器工作溫度為: -40～55 ℃[19],因此可通過優化工作周期使電容器處于正常工作溫度范圍內,對于保證電容器穩定運行尤為重要。假定單個充放電周期對電容器施加熱載荷為P0,發熱功率為Q;n次電容器發熱功率為Qn,可以得到:

為了驗證不同工作周期對電容器持續工作溫升的影響,通過施加不同熱載荷,可以得到不同模型穩態溫度分布和最高點溫度變化見表6。

表6 不同工作周期電容器仿真穩態溫度Tab.6 Comparison of steady-state temperature simulation of capacitors with different working periods

由表6 可知,電容器在工作溫度范圍內,適當加長工作周期能有效降低電容器工作內部溫升。通過仿真計算可知,電容器運行溫升最低最優方案為: 工作周期為8 s 的設計方案。

6 結論

本文分析了金屬化膜電容器熱傳導過程和金屬化膜導熱各向異性。基于以上條件建立電容器仿真模型,研究了脈沖用電容器穩態溫度,試驗結果驗證了仿真模型的準確性。在額定工況下,電容器工作過高溫升會影響其工作性能,合理優化電容器金屬化膜卷繞參數和工作周期參數設置對脈沖電容器設計有一定指導意義。