基于IRLS的跳頻模式下GTD散射參數提取和RCS重構

李英俊, 劉永祥, 田 彪, 張文鵬

(國防科技大學電子科學學院, 湖南 長沙 410073)

0 引 言

雷達散射截面(radar cross section, RCS)[1]為研究雷達目標特性[2-3]、雷達目標成像[4-5]和雷達目標識別[6-7]提供了數據基礎。RCS既與目標自身結構和材質有關,又受到入射電磁波的影響,還與目標姿態有關,是雷達目標在特定頻域、角域和極化域的固有表征。當前獲取RCS數據的主要方式包括電磁仿真、暗室測量和外場實測[8-10], 然而這些方法均存在數據存儲空間大、測試周期長等問題。如何有效降低RCS數據獲取的時空開銷是人們研究的重要方向。

在光學區,雷達目標的后向散射回波可以等效為多個獨立散射中心后向散射回波的相干合成[11]。衰減指數(damped exponential, DE)和模型[12-13]能夠表征理想點散射現象,但不能表征復雜的電磁散射行為,其使用條件受到相對帶寬的制約。基于幾何繞射理論(geometric theory of diffraction, GTD)模型[14-15]能夠貼切地反映電磁散射機理和精準地表征鏡面反射、邊緣繞射、尖頂散射等散射現象。該模型的使用條件幾乎不受相對帶寬的制約,現已廣泛用于雷達自動目標識別等領域。

基于現代譜估計的GTD散射參數提取方法已經取得了較好的研究成果,如多重信號分類(multiple signal classification, MUSIC)算法[16-18]、基于旋轉不變技術的信號參數估計(estimating signal parameter via rotational invariance techniques, ESPRIT)算法[19-21]、矩陣增強和矩陣束(matrix enhancement and matrix pencil, MEMP)[22-24]算法等。然而,該類方法不能處理非均勻不完備的RCS數據,并且其頻率依賴因子在級數展開時也會引入高階近似誤差。此外,通過暗室測量獲取完備的RCS數據也需要巨大的時空開銷。

針對上述問題,本文將稀疏重構理論和GTD散射模型相結合對目標RCS數據建模,提出了一種基于迭代加權最小二乘(iteratively reweighed least squares,IRLS)算法的跳頻模式下GTD散射參數提取和RCS重構方法。首先,介紹了GTD散射模型并給出了暗室步進頻RCS測量在跳頻模式下的稀疏表征。然后,針對該稀疏模型引入IRLS算法,并基于稀疏最優解進行了散射參數提取和RCS重構。最后,仿真數據和電磁計算數據用于驗證所提方法的有效性。實驗結果表明,所提方法可以在RCS數據非均勻不完備的條件下反演GTD散射參數,能夠實現精準RCS重構,對縮減暗室RCS測量的時空開銷具有重要意義。

1 GTD模型及其稀疏表征

1.1 GTD模型

在光學區,雷達目標電磁散射可等效為多個局部強散射中心的相干合成[11]。因此,任意復雜目標的后向散射場總可由鏡面散射、邊緣散射、尖頂散射、凹腔體散射、行波蠕動波散射等近似表征。根據GTD散射模型,光學區目標的后向散射回波可以表征為

(1)

式中:y表示雷達目標的后向散射回波;I表示等效散射中心的個數;f0表示發射信號的初始頻率;c表示電磁波的傳播速度;Ai示第i個散射中心的散射強度;αi表示第i個散射中心散射類型[11];ri表示第i個散射中心在雷達視線上的距離。5種散射類型對應的典型散射結構如表1所示。

表1 典型散射結構的散射類型α取值

步進頻暗室RCS測量系統通過依次發射相干步進頻信號工作[25-26]。假設相干步進頻信號的頻率間隔為Δf,則第n個步進頻信號的頻率為fn=f0+nΔf(n=0,1,…,N-1)。因此,步進頻暗室RCS測量等效于對式(1)作均勻離散化處理:

(2)

式中:yn表示雷達目標在頻率fn處的RCS數值。相應地,信號帶寬為B=(N-1)Δf,最大無模糊距離為RU=c/2Δf,徑向距離分辨率為Δr=c/2B。

1.2 稀疏表征

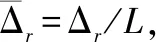
(3)

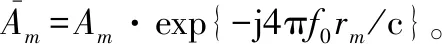
在掃頻RCS測量模式下,步進頻暗室RCS測量系統需要對待測目標進行全頻帶掃頻測試。在測量帶寬為B=N(-1)Δf的假設下,每個姿態均需要進行N次掃頻測試。而在跳頻RCS測量模式下[27-28], 步進頻暗室RCS測量系統只需要從上述N個待測頻點中隨機抽取Q個頻點進行測量,之后通過RCS重構進而實現全頻帶RCS等效測量的目的。

假設V為跳頻RCS測量模式下被測頻率索引構成的集合,則集合V共包含Q個元素且集合V?[0,1,…,N-1]T。為了便于描述,定義稀疏度ρ如下:

(4)

式中:ρ∈[0,1]是跳頻RCS測量模式下的實際被測頻點數與掃頻RCS測量模式下的理論被測頻點數的比值。ρ表征了跳頻RCS序列的稀疏程度,其值越小表征稀疏程度越高。

由于同一個距離網格rm上可候選5種不同的散射類型αrm={-1,-0.5,0,0.5,1}[29],考慮系統加性噪聲的影響,將式(3)寫成矩陣形式:

y=SΦx+w

(5)

Φ=[Φr0,Φr1,…,ΦrL(N-1)-1,ΦrL(N-1)]

(6)

式中:Φrm(m=0,1,…,L(N-1)) 是一個N×5的子矩陣,包含了5種候選的散射類型。因此,Φrm可進一步寫成

Φrm=[Φαrm =-1,Φαrm =-0.5,Φαrm =0,Φαrm =0.5,Φαrm =1]

(7)

式中:Φαrm∈CN×1為冗余字典矩陣Φ的基向量。根據式(3),Φαrm∈CN×1可被確定為

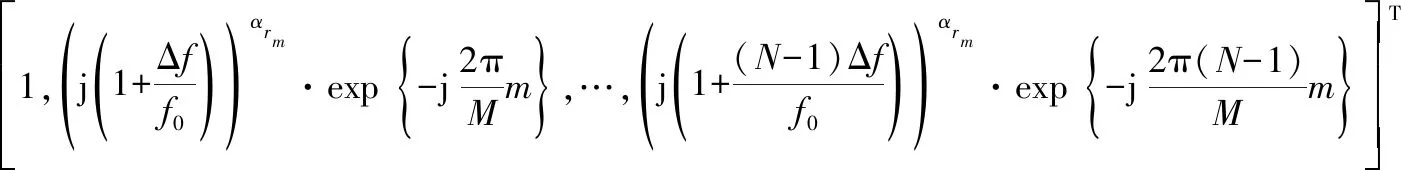
(8)

為了便于分析,記

(9)

2 散射參數提取及RCS重構

2.1 基于IRLS算法的稀疏求解

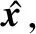
式(5)是一個欠定逆問題,包含了無窮多組解。為了避免直接對l0范數優化求解,IRLS算法將最小l0范數優化問題轉化為最小lp范數優化問題:

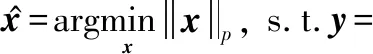
(10)

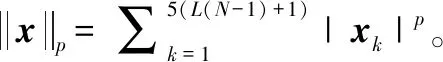
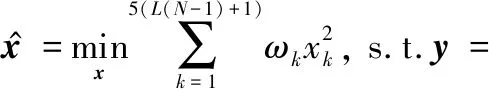
(11)

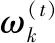
(12)

(13)

式(13)表明,IRLS算法可以通過IRLS準則來快速近似求解最小化lp范數優化問題。因此,基于IRLS算法稀疏優化求解的關鍵是對式(11)中的目標函數進行優化求解。

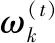
(14)

相應地,權重系數矩陣W(t)為

(15)

將式(15)中的權重系數矩陣代入下式即可實現x的第t次更新x(t):

x(t)=W(t)H(HW(t))-1y

(16)

式中:(·)H表示共軛轉置運算;(·)-1表示矩陣求逆運算。為了加快收斂速度,正則化參數ε(t)可根據下式更新:

(17)

2.2 散射參數提取和RCS重構

(18)

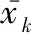
(19)

式中:floor(·)表示向下取整函數; mod(·)表示取余函數。

(20)

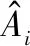
(21)

根據式(6)～式(8),其散射類型為

(22)

因此,雷達目標后向散射回波的等效散射中心的位置、強度和類型均可以根據式(20)～式(22)確定。進一步,將提取的散射參數代入下式即可實現跳頻RCS重構:

(23)

2.3 算法流程框圖

綜上所述,本文提出的基于IRLS的跳頻模式下,GTD散射參數提取和RCS重構方法可分為3個步驟。

步驟 1稀疏建模,基于雷達系統參數建立式(5)模型。

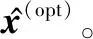
步驟 3散射參數提取和RCS重構,基于式(20)～式(22)確定散射參數和基于式(23)完成跳頻RCS重構。所提方法的流程如圖1所示。

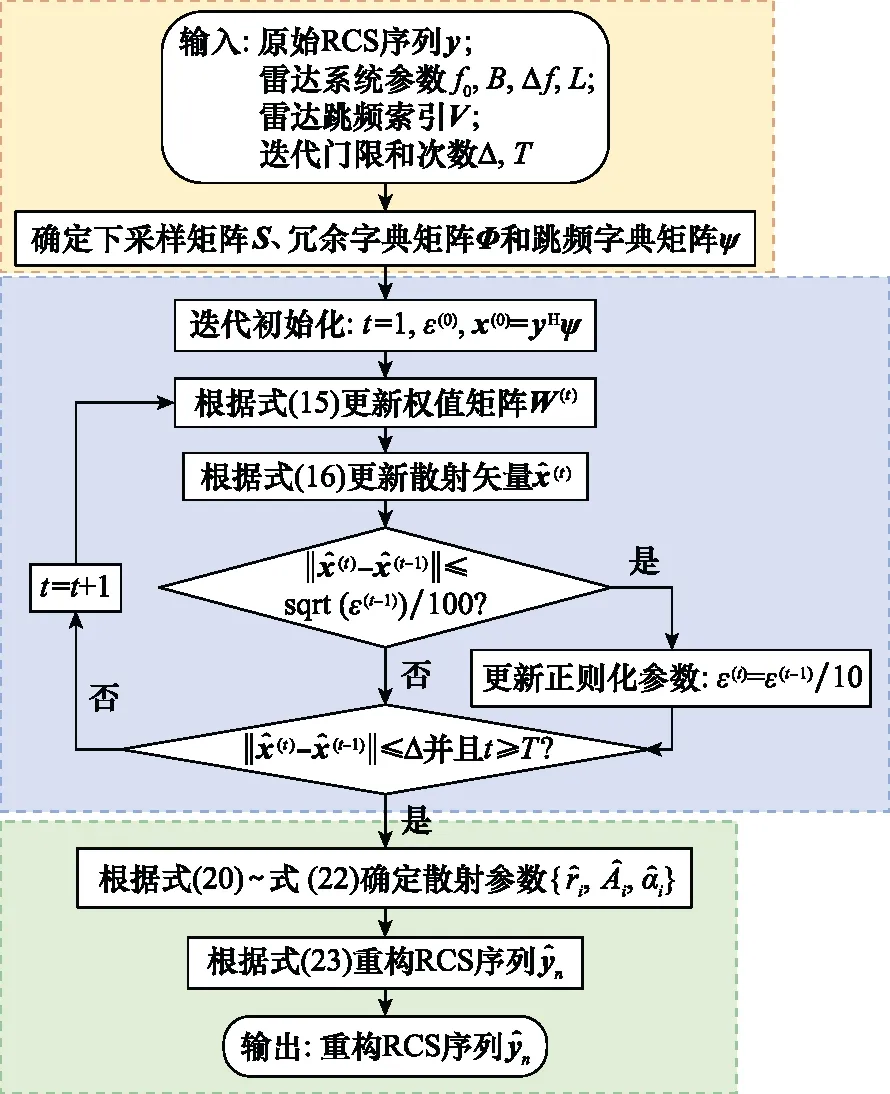
圖1 所提方法的流程圖Fig.1 Flowchart of the proposed method

3 實驗驗證與分析

3.1 仿真數據測試結果與分析

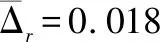
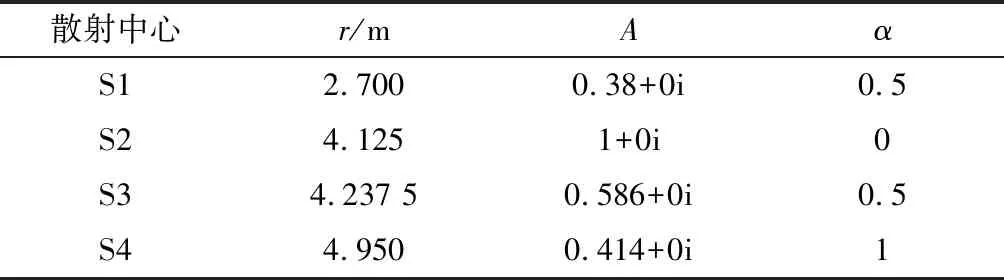
表2 仿真目標散射中心參數

3.1.1 散射參數提取和RCS重構可行性驗證

為了驗證所提方法散射參數提取的可行性,分別對原始RCS序列(稀疏度ρ=100.0%)和稀疏度ρ=50.0%的跳頻RCS序列進行散射參數提取。仿真實驗中加入了信噪比(signal to noise ratio, SNR)為25 dB的加性復高斯白噪聲。對原始RCS序列(稀疏度ρ=100.0%)和稀疏度ρ=50.0%的跳頻RCS序列分別進行100次Mont Carlo仿真,3類散射參數的平均結果如表3所示。對表3的數值結果作可視化分析,其結果如圖2所示。

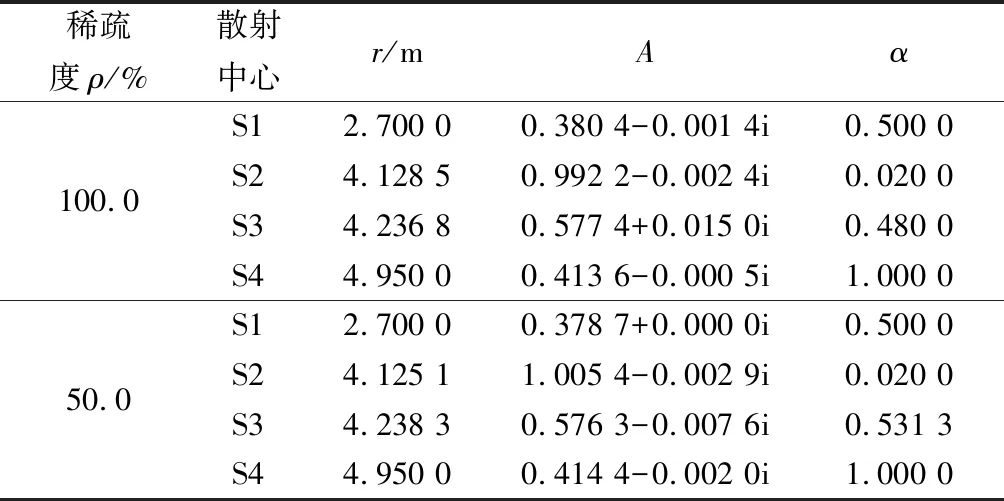
表3 SNR=25 dB時兩種稀疏條件下仿真結果均值

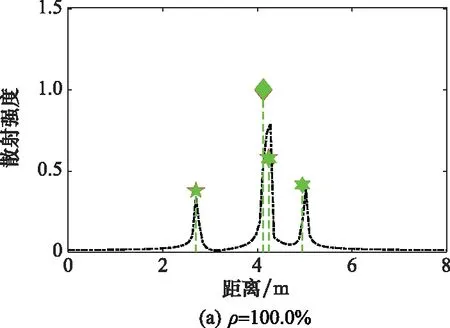
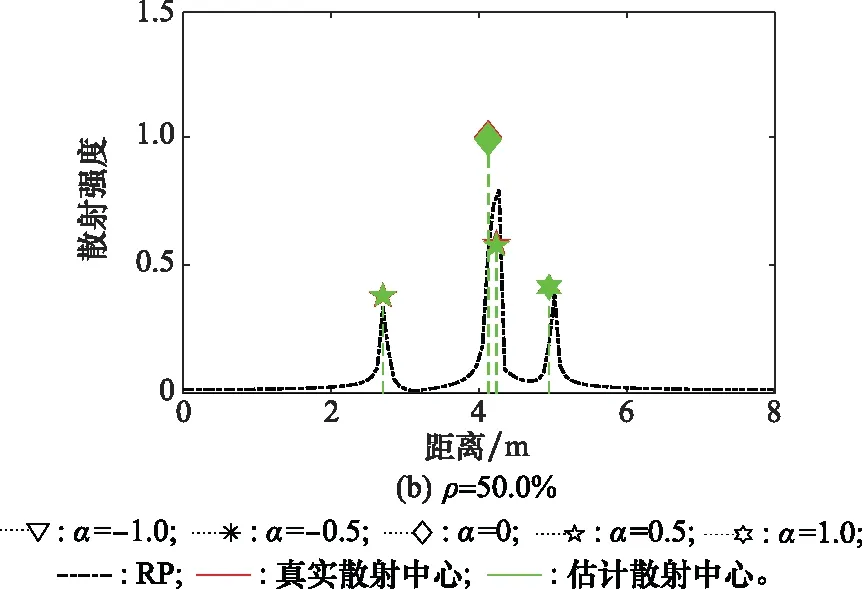
圖2 信噪比SNR=25 dB時兩種稀疏條件下仿真結果比對Fig.2 Simulation result comparison under two sparse conditions when SNR=25 dB

表3數據表明,SNR=25 dB時所提方法可以在上述兩種條件下實現散射參數提取,且二者的提取結果與真實值相一致。圖2直觀地驗證了上述結論:4個散射中心的散射位置、散射強度和散射類型均被正確估計,僅散射強度存在一定偏差,驗證了所提方法散射參數提取的可行性。

為了驗證所提方法RCS重構的可行性,在SNR=25 dB的條件下,分別對原始RCS序列(稀疏度ρ=100.0%)和稀疏度為50.0%的跳頻RCS序列進行散射參數提取,并通過式(23)進行RCS重構。定義重構誤差百分比(percentage of reconstruction error, PRE)如下:

(24)

對原始RCS序列(稀疏度ρ=100.0%)進行仿真實驗,本文方法和文獻[18]中方法的重構結果及PRE如圖3所示。

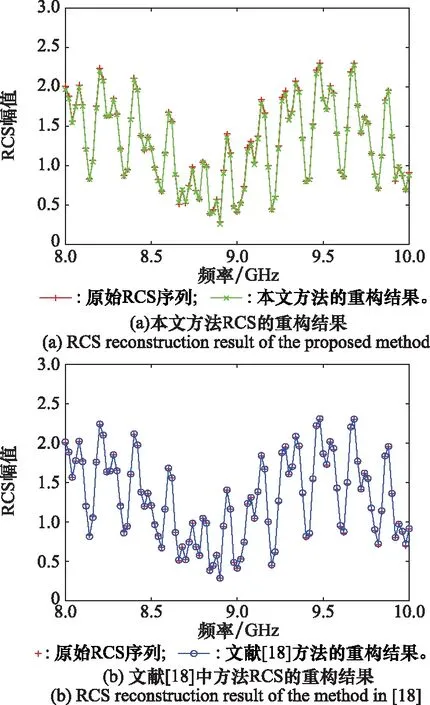
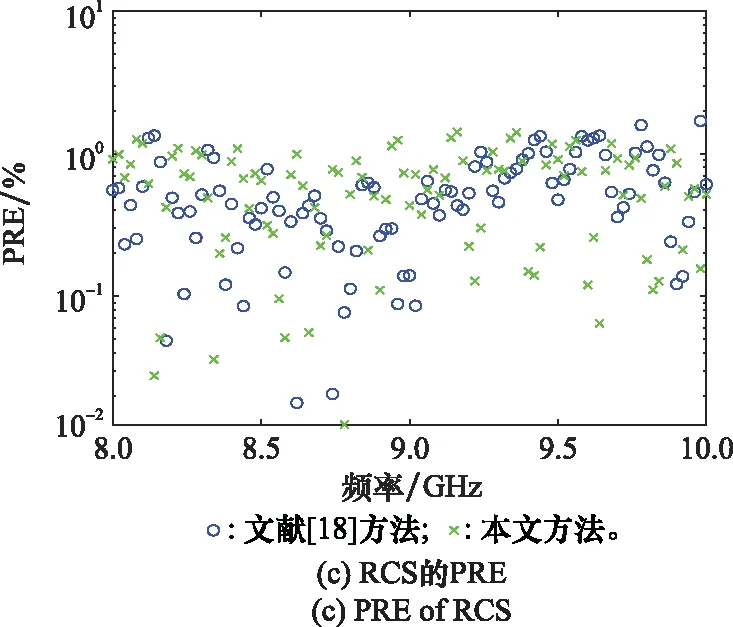
圖3 稀疏度ρ=100.0%時的RCS重構Fig.3 RCS reconstruction when ρ=100.0%

圖3表明,稀疏度ρ=100.0%時兩種方法均能準確地重構了RCS序列。經計算,本文方法PRE的均值和最大值分別為0.626 7%和1.419 2%;文獻[18]中方法的PRE的均值和最大值分別為0.572 9%和1.698 5%。這表明,在RCS序列完備的條件下，所提方法的重構性能與文獻[18]所提方法的重構性能可以相比擬。

進一步,在稀疏度ρ=50.0%的條件下對本文方法和文獻[18]中方法進行仿真實驗。由于文獻[18]中方法不能處理非均勻數據,因此，該方法處理的跳頻RCS序列為均勻下采樣序列,而本文方法處理的跳頻RCS序列為隨機下采樣序列。兩種方法的重構結果及PRE如圖4所示。

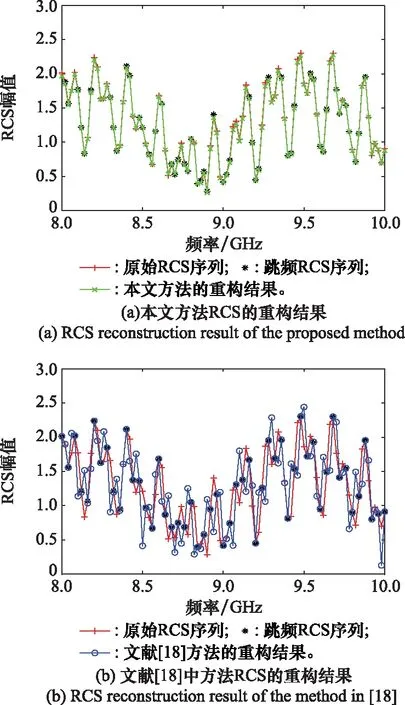
圖4 稀疏度ρ=50.0%時的RCS重構Fig.4 RCS reconstruction when ρ=50.0%

圖4表明,在稀疏度ρ=50.0%的條件下所提方法能夠準確地重構RCS序列,其PRE的均值和最大值分別為1.439 8%和3.745 2%。文獻[18]中方法的重構結果與原始RCS序列存在較大偏差,其PRE的均值和最大值達到了18.582 8%和65.333 7%。實驗結果表明,所提方法可以在RCS數據非均勻不完備的條件下工作,驗證了其可行性。

3.1.2 散射參數提取和RCS重構性能分析

為了進一步研究稀疏度對散射參數提取和RCS重構的影響,定義均值均方誤差(mean mean square error, MMSE)如下:

(25)

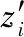
(26)

(27)

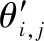
為了研究稀疏度對散射參數提取的影響,在稀疏度為10%～100%內每間隔10%進行100次Mont Carlo仿真,散射位置和散射強度的MMSE(MMSEr和MMSEA)以及散射類型錯誤率隨稀疏度的變化如圖5所示。

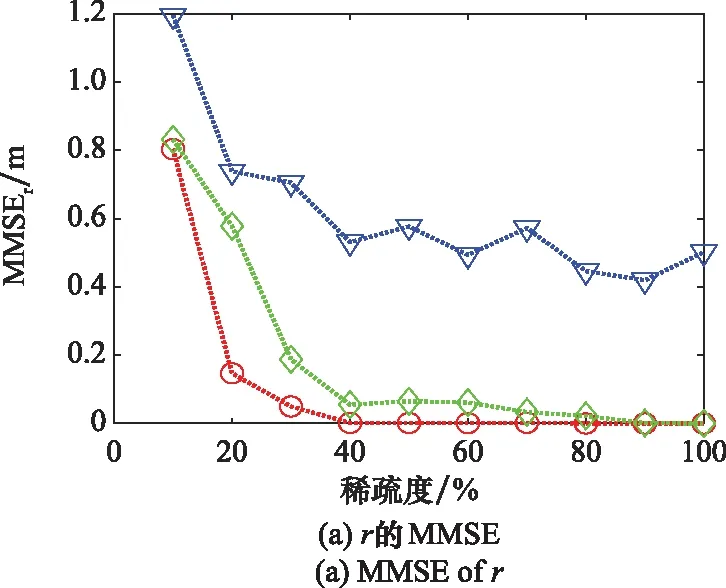
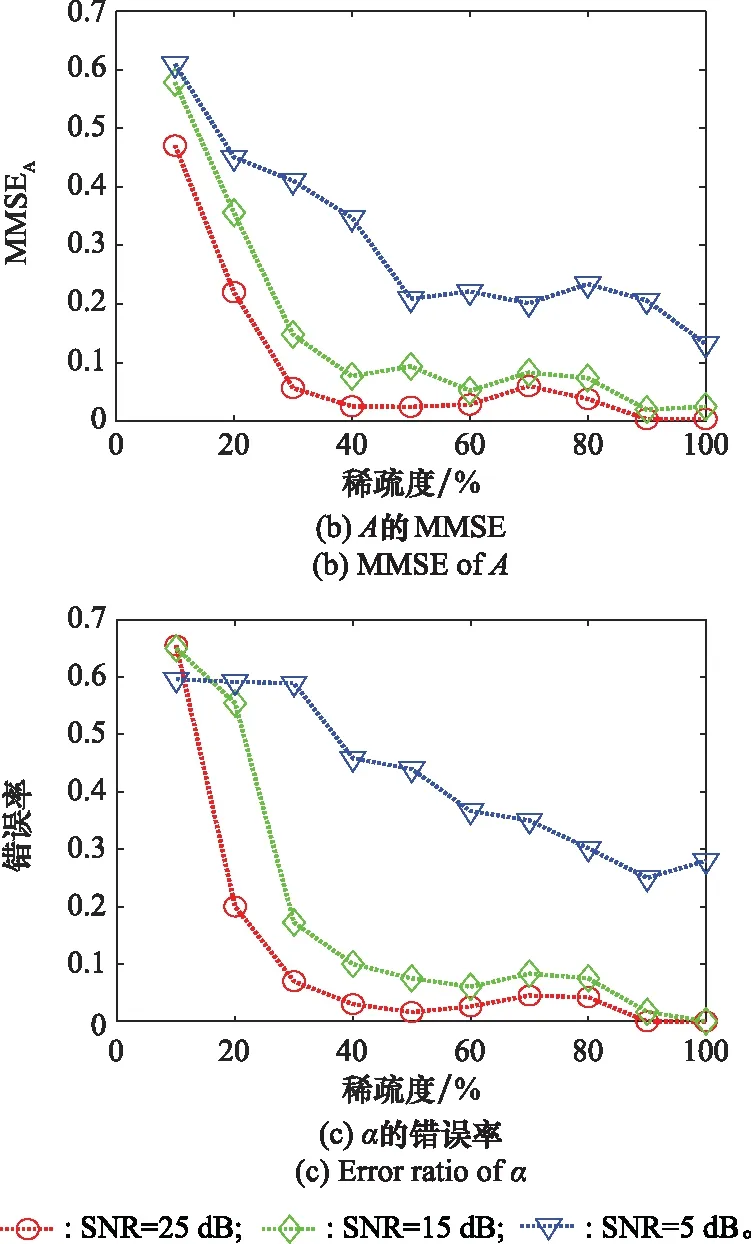
圖5 稀疏度ρ對散射參數提取精度的影響Fig.5 Influence of ρ on the accuracy of scattering parameter extraction

圖5表明,當稀疏度為10%～40%時,MMSEr、MMSEA和散射類型錯誤率迅速降低。這是因為稀疏度過低時等距約束條件(restricted isometry property, RIP)被破壞(將在下文分析),散射參數不能被準確估計;而隨著稀疏度的增加,RIP條件逐漸得到滿足,進而導致MMSEr、MMSEA和散射類型錯誤率迅速降低的現象。當稀疏度為40%～100%時,MMSEr、MMSEA和散射類型錯誤率逐漸降低并趨于平穩。這表明,在此稀疏條件下散射參數可以被準確估計,其提取精度幾乎不受稀疏度的影響。

對比圖5可得,與MMSEA和散射類型錯誤率相比,MMSEr在高信噪比和高稀疏度下更為穩定,而MMSEA和散射類型錯誤率在稀疏度為60%～90%時存在一定波動。這表明,相比于散射強度和散射類型參數的提取,散射位置參數的提取更為準確。

對比圖5中3種不同SNR下的MMSEr、MMSEA和散射類型錯誤率還可得,SNR=25 dB時散射參數的提取精度依次高于SNR=15 dB和SNR=5 dB時散射參數的提取精度。這表明,散射參數的提取精度還受到SNR的影響,且在相同稀疏條件下SNR越高散射參數的提取精度也越高。

為了研究稀疏度對RCS重構的影響,對上述提取的散射參數通過式(23)進行RCS重構。重構RCS序列的幅值(amplitude, Amp)和相位(phase, Pha) 的MMSE (MMSEAmp和MMSEPha)隨稀疏度的變化如圖6(a)和圖6(b)所示。

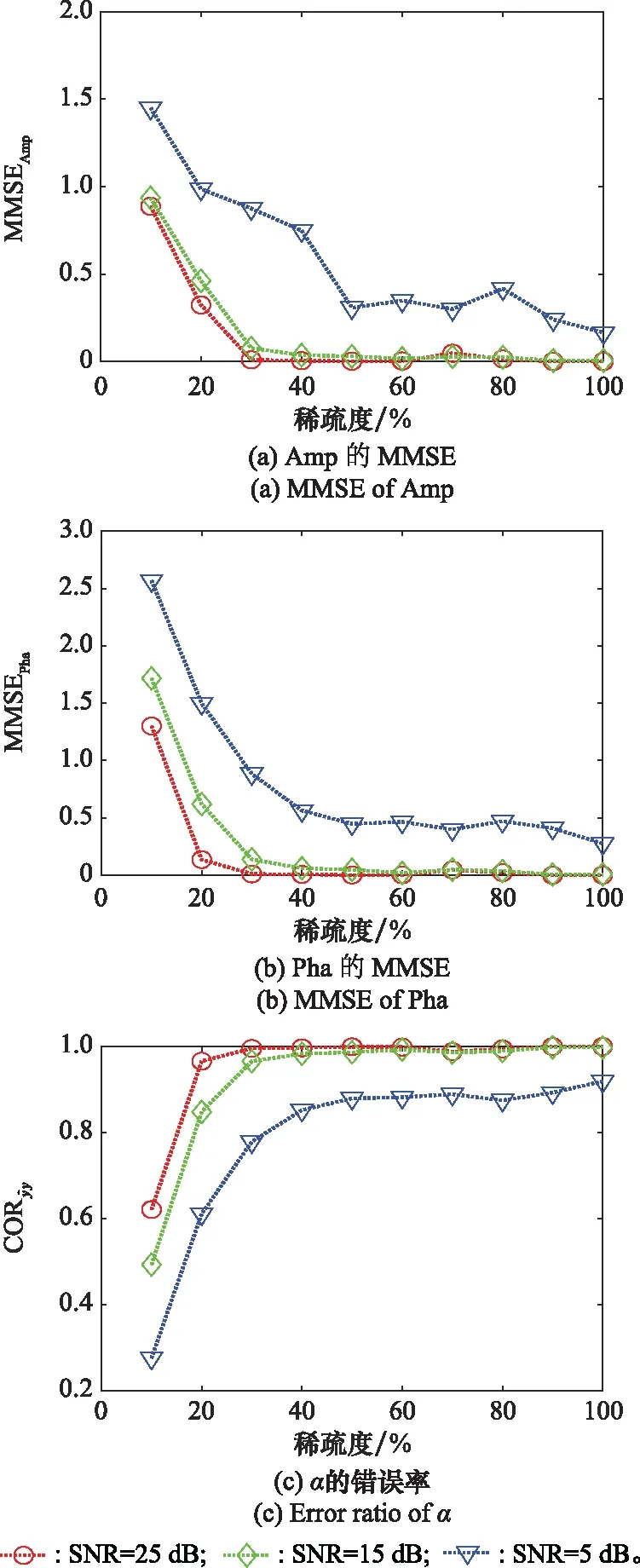
圖6 稀疏度ρ對RCS重構精度的影響Fig.6 Influence of ρ on the accuracy of RCS reconstruction

為了更合理地評估RCS的重構質量,定義相似度 (correlation,COR)如下:

(28)

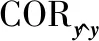
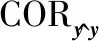
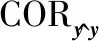
圖5和圖6的仿真結果表明,散射參數提取精度和RCS重構精度均具有隨稀疏度增加先急劇提升再逐漸趨于平穩的變化趨勢。對比圖5和圖6還可得,相比于RCS重構,散射參數提取所需的稀疏邊界值略高。上述結果表明,準確的散射參數提取可以確保準確的RCS重構;但同時也表明,與準確的RCS重構相比,準確的散射參數提取所需的稀疏邊界值略高。

3.2 電磁計算數據測試結果與分析

為了驗證所提方法的有效性,分別利用兩段圓錐組合體和F117飛機的電磁計算數據進行實驗驗證。

3.2.1 兩段圓錐組合體電磁計算數據

在本實驗中,電磁仿真目標是一個圓頂的兩段圓錐組合體,其CAD模型如圖7所示。雷達初始視線沿Z軸指向仿真目標的鼻錐方向。雷達仿真參數設置如下:初始頻率f0=8 GHz,雷達帶寬B=2 GHz,步進頻率間隔Δf=20 MHz (N=101),方位角間隔為Δθ=0.05°,方位角為0°～180°。

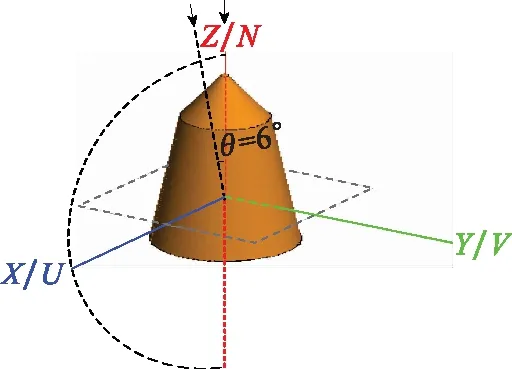
圖7 兩段圓錐組合體的CAD模型Fig.7 CAD model of two-stage cone assembly

由圖7可得,該目標的后向散射回波主要包含圓頂錐頭的鏡面反射分量、兩段圓錐結合處的邊緣繞射分量和目標底部的邊緣繞射分量。方位角累積角θ=0°～6°對應的原始RCS序列如圖8(a)所示。在頻率維對原始RCS序列進行稀疏度ρ=50.0%的隨機下采樣,其跳頻RCS序列如圖8(b)所示。為了驗證所提方法的有效性,對圖8(b)所示的跳頻RCS序列進行散射參數提取,并通過式(23)進行RCS重構,其重構結果如圖8(c)所示。

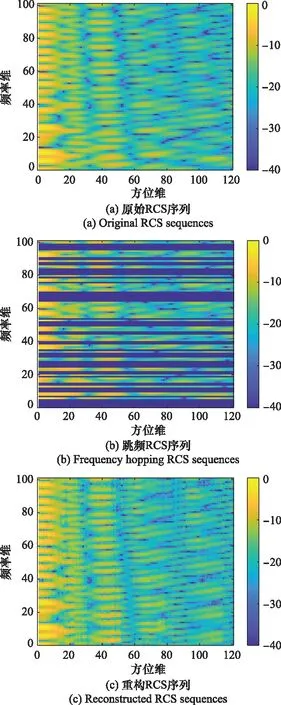
圖8 兩段圓錐組合體的RCS序列Fig.8 RCS sequences of the two-stage cone assembly target

對比圖8(a)和圖8(c)可知得,重構RCS序列與原始RCS序列高度吻合。經計算,二者的峰值SNR (peak SNR, PSNR)為PSNR=39.099 9 dB。

為了進一步評估RCS的重構質量,采用距離多普勒算法(range Doppler, RD)對圖8中原始RCS序列、跳頻RCS序列和重構RCS序列進行逆合成孔徑雷達(inverse synthetic aperture radar, ISAR)成像,其ISAR像的結果如圖9所示。

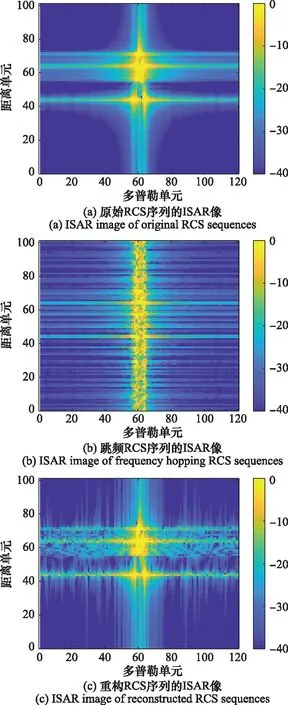
圖9 兩段圓錐組合體的ISAR像Fig.9 ISAR image of the two-stage cone assembly

由于RCS數據大量缺失,圖9(b)中跳頻RCS序列的ISAR像在距離向存在嚴重散焦現象,無法辨識仿真目標。經計算,該ISAR像與圖9(a)中原始RCS序列的ISAR像的PSNR和均方根誤差(root mean square error,RMSE)分別為31.161 7 dB和5.364 1e-04。相比于圖9(b),圖9(c)中重構RCS序列的ISAR像則有效避免了在距離向上的散焦現象,可辨識仿真目標,其成像結果與圖9(a)高度相似。經計算,二者的PSNR和RMSE分別為38.315 3 dB和8.595 0e-05。

圖10給出了兩段圓錐組合體在θ=1.05°時后向散射回波的散射參數提取結果和RCS重構結果。圖10(a)表明該散射回波可由5個等效散射中心構成,其散射位置和散射強度與雷達一維距離像(range profile, RP)相吻合。此外,該散射回波主要由鏡面反射、邊緣繞射和理想點散射分量構成,與仿真目標的幾何結構基本吻合。由于散射結構間的相互耦合及散射中心偏離網格的影響,兩段圓錐結合處的另一散射中心和圓錐底部的另一散射中心均被判定為理想點散射類型。由圖10(b)可得,重構RCS序列與原始RCS序列的Amp高度吻合,僅在8.3 GHz (PRE=64.501 5%)處存在較大偏差。經計算,其PRE的均值為13.900 4%。

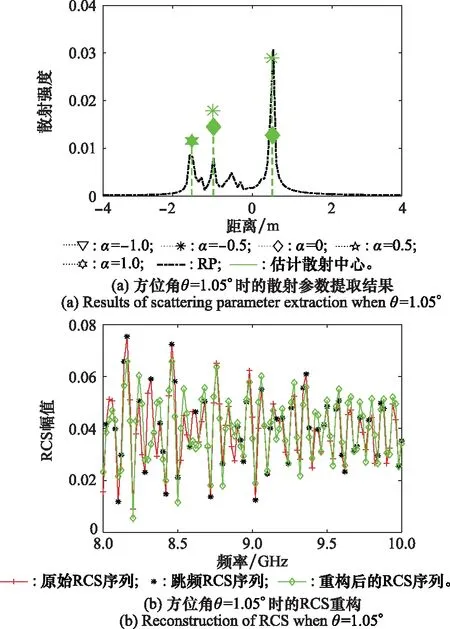
圖10 兩段圓錐組合體散射參數提取和RCS重構Fig.10 Scattering parameter extraction and RCS reconstruction of two-stage cone assembly

3.2.2 F117飛機電磁計算數據

在本實驗中,仿真目標是F117飛機,其CAD模型如圖11所示。雷達初始視線沿Z軸指向仿真目標的機頭方向。雷達仿真參數設如下:初始頻率f0=9.5 GHz,雷達帶寬B=1 GHz,步進頻率間隔Δf=5 MHz(N=201),方位角間隔為Δθ=0.000 70°,方位角為0°～360°。

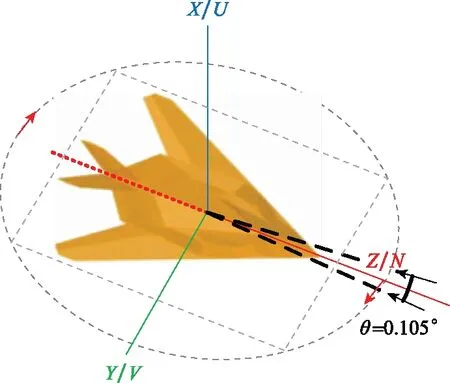
圖11 F117飛機CAD模型Fig.11 CAD model of F117 aircraft

方位累積角θ=-0.052 5°～0.052 5°對應的原始RCS序列如圖12(a)所示。稀疏度ρ=50.0%時,對應的跳頻RCS序列如圖12(b)所示。依次對圖12(b)所示的跳頻RCS序列進行散射參數提取,并通過式(23)進行RCS重構,其重構結果如圖12(c)所示。對比圖12(a)和圖12(c)可知,重構RCS序列與原始RCS序列高度相似。經計算,二者的PSNR為53.212 6 dB。類似地,采用RD算法分別對該目標的原始RCS序列、跳頻RCS序列和重構RCS序列進行ISAR成像,其成像結果如圖13所示。

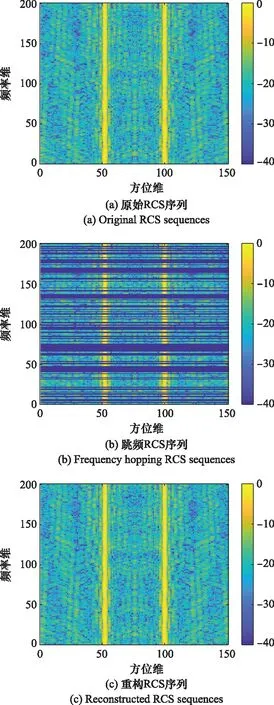
圖12 F117飛機的RCS序列Fig.12 RCS sequences of F117 aircraft

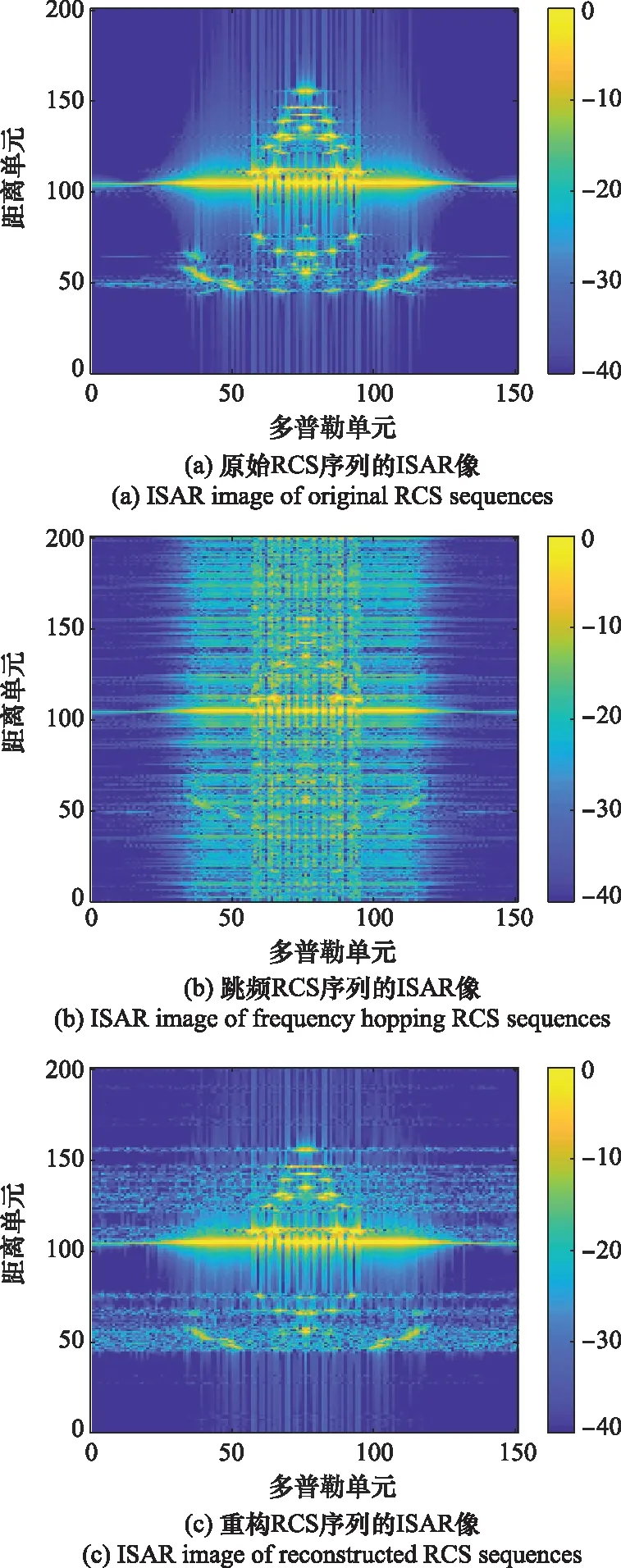
圖13 F117飛機的ISAR像Fig.13 ISAR image of F117 aircraft

圖13(b)中跳頻RCS序列的ISAR像在距離向存在嚴重散焦現象,該ISAR像與圖13(a)中原始RCS序列的ISAR像的PSNR和RMSE分別為42.4151 dB和1.145 1e-04。相比于圖13(b),圖13(c)中重構RCS序列的ISAR像則有效避免了在距離向上的散焦現象,可辨識仿真目標,其成像結果與圖13(a)中原始RCS序列的ISAR像高度相似,二者的PSNR和RMSE分別為54.454 8 dB和5.323 0e-06。

圖14給出了F117飛機在θ=0°時后向散射回波的散射參數提取結果和RCS重構結果。圖14(a)表明該散射回波可由24個等效散射中心構成,散射位置和散射強度與雷達一維RP高度吻合。此外,該散射回波主要由鏡面反射、理想點散射和邊緣繞射構成,與F117飛機的幾何結構基本吻合。由圖14(b)可得,重構RCS序列與原始RCS序列的Amp幾乎完全擬合,僅在峰值和峰谷處存在一定偏差,最大偏差發生在9.63 GHz (PRE=48.382 2%)。經計算,其PRE的均值為12.521 5%。

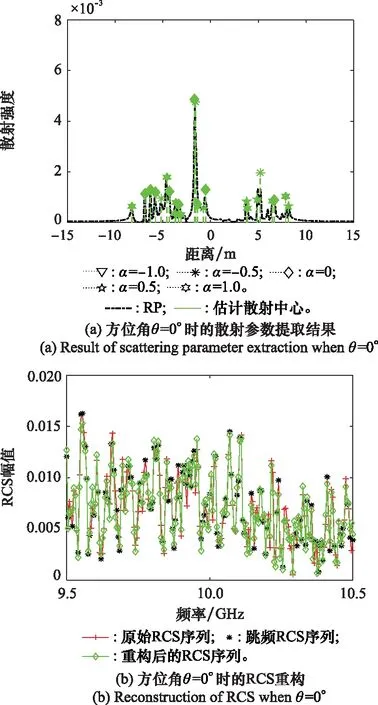
圖14 F117飛機散射參數提取和RCS重構Fig.14 Scattering parameter extraction and RCS reconstruction of F117 aircraft

圓錐組合體和F117飛機的實驗結果表明,所提方法可以在RCS數據非均勻不完備的條件下反演散射參數和實現RCS重構。散射中心提取結果、RCS重構結果以及ISAR成像結果均驗證了所提方法的有效性,并表明所提方法可以用于縮減暗室RCS測量所需的時空開銷。

4 結 論

本文利用雷達目標RCS數據中蘊含的特征信息,將稀疏重構理論與GTD散射模型相結合,提出了一種基于IRLS的跳頻模式下GTD散射參數提取和RCS重構方法。仿真數據和電磁計算數據驗證了所提方法的可行性和有效性。實驗結果表明,所提方法可以在RCS數據非均勻不完備的條件下反演散射參數和重構RCS序列,對降低暗室步進頻率RCS的測量成本、擴增雷達RCS的數據具有重要意義。