非正態響應穩健參數設計的貝葉斯建模與優化

馬 妍, 汪建均,*, 馮澤彪

(1. 南京理工大學經濟管理學院, 江蘇 南京 210094; 2. 南京郵電大學管理學院, 江蘇 南京 210003)

0 引 言

20世紀70年代,日本著名的質量工程專家田口玄一(Genichi Taguchi)博士以正交試驗設計和信噪比為基礎提出了穩健參數設計方法。穩健參數設計旨在通過選擇可控因子的最佳設置,以減少或控制噪聲因子對產品或過程波動的影響,從而設計出對噪聲因子變化不敏感的產品或過程。現代質量工程的主流觀點認為:波動是導致質量問題產生的根本原因。盡管人們無法完全消除由噪聲因素所導致的波動,但是可以對其進行減小或控制[1]。通常情況下,噪聲因子可以在試驗過程中被控制,但不能在工藝操作或產品使用過程中被控制。噪聲因子就是在正常生產過程或使用條件下難以被控制的因子[2-3]。噪聲因子包括很多類型,常見的表現形式有:① 工藝參數的變化。例如,反應罐中的溫度很重要,如果要考慮由其變化所產生的影響,通常將其視為可控因子。但是,溫度在實際生產中會產生波動,因此通常要將溫度這個參數的波動看成噪聲因子。② 原材料參數的變化。在制造過程中,零部件的實際值與名義值總會有偏離。由于原材料參數通常被視為可控因子,此類誤差所形成的噪聲因子也被稱為“內噪聲”。③ 環境的變化。環境條件對響應變量也會有直接的影響,而通常又未被納入可控因子的范圍內。例如,溫度、濕度、輸入電壓等環境的變化可能會直接影響輸出響應的波動。上述隨著使用條件和環境變化的波動通常被視為外干擾,也稱為“外噪聲”。此外,產品所承受的外部載荷、元器件的耗損降級等噪聲因素也可能會引起輸出響應的波動。

在產品生產過程或用戶使用過程中,噪聲因子時刻影響產品或過程的穩健性能。如何有效地減小或控制噪聲因子對產品或過程輸出響應的波動,構成了穩健參數設計的核心內容。盡管Taguchi的質量哲學思想已被學術界所普遍接受,但其方法在穩健參數設計的實現技術[4]存在相當大的爭議[5],如信噪比效率低下、設計變量缺乏靈活性、正交試驗無法考慮因子之間的交互效應、試驗設計計劃缺乏經濟性等。為此,一些統計學家提出了響應曲面方法(response surface methodology, RSM)。RSM[6]是由響應曲面設計、經驗模型構建和數值優化技術所組成的系統科學方法。RSM已被廣泛地應用于各種產品或過程的質量設計,在連續質量改進活動中提供。著名的統計學家Myers等[7]指出,從更為廣泛的意義上看,RSM已成為工業試驗的核心。因此,一些統計學家使用RSM來實現產品或過程的穩健參數設計。例如,著名的質量專家Myers[8]曾在質量領域的國際期刊《Journal of Quality Technology》上發表了一篇非常有影響力的綜述性論文。在這篇代表性的綜述論文中,Myers[8]指出，在過去的20多年內,RSM在穩健參數設計研究中作為方差縮減和過程改進的替代方法備受關注。RSM正轉向廣義線性模型(generalized linear model, GLM)的使用,包括以logistic和泊松回歸為例的應用研究。此外,其他的RSM還包括多響應優化方法、非參數方法和半參數方法。隨著計算機模擬技術的發展,以RSM為基礎的模擬建模與優化方法也引起了相關學者的廣泛關注。例如,著名學者Kleijnen[9]曾圍繞上述的研究問題,從模擬優化的視角展開了深入的分析與總結,在國際期刊《European Journal of Operational Research》發表了有代表性的綜述論文。

在工業試驗的數據分析中,RSM作為傳統Taguchi方法的替代方法,有效地彌補了Taguchi方法的不足之處。例如,Myers等[10]借鑒了Taguchi所提出的穩健參數設計基本思想,提出了一種非常具有吸引力的替代方法——RSM方法。首先,假設噪聲因子在某種已知分布的范圍內變化。然后,通過響應曲面設計所獲得的試驗數據,分別擬合輸出響應與可控因子、噪聲因子之間的均值模型和方差模型,即雙響應曲面模型[11]。最后,借鑒Taguchi穩健設計思想對其進行最優化(即在最小化響應均值與設計目標值之間的偏差的同時,最大限度地減小響應方差),以獲得理想的可控因子設計值。上述的雙響應曲面建模方法非常巧妙地回避了Taguchi方法在實現穩健參數設計時所面臨的一些有爭議性的技術問題。需要指出的是,傳統的方法(如RSM方法、Taguchi方法等)通常假定響應數據滿足正態或同方差。然而,在實際的質量設計中,分析人員經常會遇到非正態響應的質量設計問題[12]。GLM方法可以看成是一般RSM方法的一種擴展,通常被視為涉及非正態響應的RSM。例如,針對非正態響應,Myers等[13]曾利用GLM來構建輸出響應與可控因子、噪聲因子之間的函數關系,從而實現了在GLM建模框架下非正態響應的穩健參數設計。

在實際生產或制造過程中,除了噪聲因素的影響,模型參數、模型結構、預測誤差等不確定性因素將在相當大的程度上影響響應曲面的建模精度與分析結果。例如,Kleijnen[9]指出,在當今的不確定性世界中,穩健優化是極其重要的,在不可控制的環境中,若忽視不確定性的影響,運用RSM或者Kriging模型所得的最優結果可能是難以令人滿意的。然而,在傳統的響應曲面設計與建模優化中,質量工程師或研究人員往往忽視了模型不確定性對試驗結果的影響[14]。

近年來,在復雜產品或先進制造過程的質量設計研究中,考慮不確定性質量設計的建模方法引發了眾多學者的研究興趣。當前,國內外學者主要運用不確定性分析方法(如置信區間[7,15-16]、模糊數學[17]、貝葉斯統計[18-23]以及組合建模[24]等)分析模型參數或模型結構的不確定性對優化結果的影響。貝葉斯方法不僅在建模過程中能夠有效地考慮以往的先驗知識和經驗信息,而且能夠在數據分析中對以往的先驗信息不斷地進行更新和修正。因此,利用貝葉斯方法開展不確定性的質量設計研究已經引起了國內外相關學者的廣泛關注和重視。例如,針對多響應優化設計問題,Peterson[25]在多變量回歸模型框架下考慮了試驗數據的相關性、模型參數的不確定性以及輸出響應的波動,通過優化輸出響應落入對應規格限的概率來獲得最優的參數設計值。Miro-Quesada等[26]擴展了Peterson的研究工作,在貝葉斯響應曲面構建中考慮了噪聲因子波動的影響,有效地刻畫了模型參數以及噪聲因子等不確定性因素對產品或過程的影響。針對多響應優化設計問題,文獻[27]在貝葉斯響應曲面建模的框架下,結合質量損失函數和后驗概率方法提出了一種新的貝葉斯優化設計方法。該方法運用貝葉斯抽樣技術獲取多響應的貝葉斯后驗樣本,并利用輸出響應的抽樣值構建了質量損失和符合性概率兩種優化度量指標,充分地考慮了模型參數不確定性以及響應波動對優化結果的影響。Ouyang等[28]基于似不相關回歸模型提出了一種貝葉斯分層建模的優化方法,同時考慮操作人員的偏好信息,提出了一種兩階段的優化策略。在此基礎上,Ouyang等[29]進一步拓展了此前的工作,在貝葉斯建模框架下考慮了變量之間的高相關性、非正態性和變量選擇問題,提出了一種基于似不相關回歸模型的馬爾可夫鏈蒙特卡羅(Markov chain Monte Carlo, MCMC)抽樣算法。該抽樣算法可以從完整的聯合后驗分布中產生后驗樣本,從而能夠獲得穩健的貝葉斯估計。此外,Yanikoglui等[30]結合模擬的試驗數據構建了同時包含可控因子和噪聲因子(或環境輸入變量)的均值和方差的雙響應曲面的元模型(或替代模型),并在此基礎上提出了一種可調節的穩健優化方法。針對噪聲因子,假設可以根據歷史數據獲得其均值、方差或協方差的信息,然后利用所觀測的噪聲因子信息來獲得可控因子的最佳設計值。結合噪聲因子的在線測量結果,Zhou等[31]提出了一種序貫的支持向量機方法,并利用該方法將前一階段的最優可控因子設置進行更新,不斷地進行迭代,從而獲得最佳的參數設計值。Jiang等[32]通過使用高保真模擬器來考慮噪聲因子的影響,提出了一種結合質量損失對數正態過程模型和高斯過程模型的新方法,來預測期望質量損失。針對可觀測的噪聲因子,Yang等[33]結合時間序列模型與貝葉斯方法,提出了一種在線穩健參數設計方法,利用該方法對期望損失函數進行實時調整,從而獲得了可控因子的最佳設計值。然而,以往的研究通常假設輸出響應服從正態分布,然后利用多項式模型或似不相關回歸模型來構建輸出響應與可控因子、噪聲因子之間的響應曲面模型。此外,如何在貝葉斯模型的框架下考慮參數不確定性以及響應的波動對優化結果的影響,如何有效地度量噪聲因子對優化結果的影響,也是穩健參數設計研究領域中非常值得關注的科學問題。

針對非正態響應的穩健參數設計問題,本文首先利用試驗數據擬合可控因子、噪聲因子以及輸出響應之間的響應曲面模型,然后結合經驗貝葉斯先驗信息獲取模型參數的抽樣值。其次,假設噪聲因子服從已知分布,并利用所估計的參數抽樣值獲取輸出響應的后驗抽樣值。最后,利用所獲的響應后驗抽樣值來構建符合性概率,并采用遺傳算法對所構建的符合性概率函數進行參數優化設計。

1 GLM的貝葉斯分析

1.1 GLM

1972年,Nelder等[34]首次提出了GLM。GLM提供了一組能夠廣泛應用于回歸分析的統一模型,不僅適用于正態響應,也適用于一些常見的非正態響應。在處理非正態響應的試驗數據時,常見的方法是利用數據轉換方法先將非正態響應轉化為正態響應。然而,數據轉換方法可能會引起多目標沖突,即要求同時滿足正態性、方差齊性和線性可加性可能導致的沖突。GLM利用聯系函數靈活地建立起響應方差與響應均值之間的函數關系,從而能夠適用于廣泛的指數族分布類型。因此,無論是連續性或是離散性的響應變量yi,均能表示為指數族的概率分布形式,其基本的表達形式如下:

f(yi|θi)=exp{a-1(φi){yiθi-φ(θi)}+c(yi;φi)}

(1)

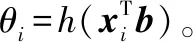
GLM的經典估計方法是極大似然方法。為了簡化起見,通常假設φi為已知的,且XT=(x1,x2,…,xn)。在上述假設下,似然函數可以表示為

(2)

與式(2)對應的得分向量為

(3)

與式(2)對應的Fisher信息矩陣為

(4)

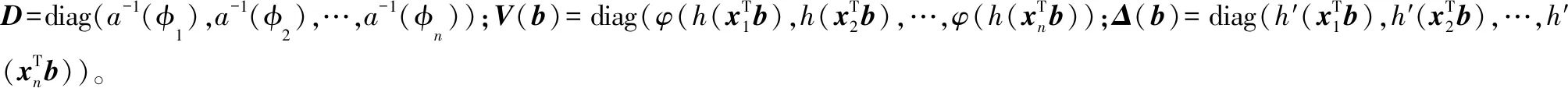
1.2 基于GLM的貝葉斯分析

在GLM的貝葉斯分析中,首先需要對模型參數給出合適的先驗分布。在式(2)中通常假設模型參數b服從N(b0,Σ),其中假設b0和Σ可以通過已知的信息獲得。在給定的試驗數據(xi,yi)下,其模型參數b的后驗分布為

(5)

通常情況下,上述參數的后驗估計難以處理[35]。事實上,在GLM框架下,上述模型參數的后驗分布往往不存在任何封閉的表達式。因此,即使是針對中等規模的模型參數,試圖通過數值積分方法來獲得模型參數的后驗均值和方差等統計量都將難以實現。針對上述問題,最為方便的方法是采用MCMC對GLM進行模擬抽樣,進而利用所獲得的后驗抽樣值進行后續的統計推斷。上述過程通常可以使用Metropolis-Hastings算法實現,但如果后驗是對數凹的,則也可以使用Gilks等[36]提出的自適應拒絕采樣(adaptive rejection sampling, ARS)方法來實現。

2 非正態響應曲面的貝葉斯建模與參數優化設計

2.1 結合因子效應原則的貝葉斯變量選擇

針對非正態響應的質量設計問題,需要考慮的首要問題是如何識別出顯著性的因子及其交互效應,即解決變量選擇問題。然而,與通常傳統回歸分析的變量選擇不同的是,在試驗設計中的變量選擇需要考慮試驗設計的因子效應原則[28](如效應稀疏、效應排序、效應遺傳)。為此,結合以往的研究經驗[10,19],在GLM的貝葉斯建模框架下,將試驗設計的因子效應原則以貝葉斯先驗信息的形式加以考慮。在此,將一個變量指示器γj納入到GLM的線性預報器ηi中,其表達式為

(6)

式中:γj為二元變量指示器;xij為輸入因子；βj為輸入因子對應的回歸系數。若變量指示器γj=1,則對應的變量包含在模型中;若變量指示器γj=0,則將對應的變量從模型中剔除出去。針對上述的二元變量指示器γj,通常假設其滿足相互獨立且概率為p的貝努利(Bernouli)分布,即

(7)

式中：pj代表變量指示器γj=1的概率,即pj=Prob(γj=1)。在缺乏先驗信息時，通常假設各變量的顯著性為等概率,即此時pj=0.5。在此,將結合試驗設計的因子效應原則來設置合理的變量顯著性概率。例如,在篩選試驗中,當主效應相對較多時,通常會根據效應稀疏原則(顯著性的因子通常是少數的,即試驗設計中的帕累托原則)將變量指示器的先驗概率pj設置為0.2。然而,Bergquist等[38]建議當主效應數目較少時,可以將變量指示器的先驗概率pj設置為0.5。變量指示器的獨立性先驗表明:一個主效應的顯著性不依賴于另外一個主效應是否顯著。然而,因子效應排序原則表明:與高階效應相比,低階效應更可能是顯著的;同階效應具有同等程度的顯著性。因此,在篩選試驗的分析過程中,通常優先考慮因子的主效應以及二階交互效應,很少考慮三階及三階以上的交互效應。此外,在考慮因子交互效應的顯著性時,需要結合因子效應遺傳原則。若因子交互項AB是顯著的,那么其親本因子A和B中至少有一個是顯著的。在篩選試驗的數據分析中,若模型僅包含交互效應而未包含所對應的親本因子,則該模型違反了試驗設計的遺傳效應原則,應該將其剔除。因此,本文將在貝葉斯建模框架中結合變量指示器的先驗概率,進一步考慮因子效應原則,從而更好地識別出顯著性因子,建立更加符合實際、更為精確的響應曲面模型。以交互效應AB為例,結合上述的因子效應原則,其交互效應AB的變量指示器的先驗概率p可以假設為

(8)

式中:(γA,γB)=(0,0)代表主效應A和主效應B都是不顯著的。在這種情況下,其交互效應所對應變量指示器的先驗概率p00通常是非常小的(如0.01)。(γA,γB)=(1,0)代表主效應A是顯著的,而主效應B是不顯著的,其交互效應所對應的變量指示器的先驗概率p10通常可以假設為比較小的數(如0.1)。(γA,γB)=(1,1)代表主效應A和主效應B都是顯著的。此時,其交互效應所對應的變量指示器的先驗概率p11可以假設為比較大的數(如0.3)。若假設所有的模型參數βj之間是相互獨立的,則針對模型參數βj,可以采用Ntzoufras[39]所提出的經驗貝葉斯先驗,其表達式為

(9)

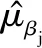
(10)

式中：T和B分別代表變量指示器后驗樣本γ(t)的總數和燃燒期(即舍棄收斂前的抽樣值)。如果變量指示器γ(t)=1,則其二元指示器I(·)=1,反之亦然。通過式(10),能夠對所考慮的變量進行顯著性排序,并根據研究的需要篩選出合適的顯著性因子或效應,以開展后續的響應曲面建模與參數優化設計。

2.2 考慮噪聲因子的貝葉斯響應曲面建模

在實驗室的環境下,某些噪聲因素(如溫度等)是可以測量和控制的。在這種情形下,研究人員通常希望能夠在試驗過程中將這些噪聲因子納入到實驗設計中,考慮利用可控因子、噪聲因子以及噪聲因子與可控因子之間的交互效應來構建響應模型,從而能夠通過選擇可控因子的最佳參數設計以減小或控制噪聲因子對產品或過程波動的影響,從而實現產品/過程的穩健參數設計。為此,結合第2.1節的因子篩選結果,將所篩選的顯著性因子劃分為可控因子x和噪聲因子z,則式(6)中GLM的線性預報器η將變為

ηi=xiβc+ziβn+xiziβcn,i=1,2,…,n

(11)

式中:xi,zi分別代表可控因子和噪聲因子的主效應;xizi代表可控因子和噪聲因子的交互效應;βc代表可控因子的估計系數;βn代表噪聲因子的估計系數;βcn代表可控因子和噪聲因子交互效應的估計系數。在此,進一步簡化式(9)的經驗貝葉斯先驗,針對式(11)中的模型參數β賦予如下的先驗形式:

(12)

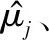
(13)

(14)

(15)

(16)

2.3 結合最小均方誤差與貝葉斯后驗概率的穩健參數優化

當第2.2節中所獲得的模擬響應抽樣值達到其穩態分布時,其響應抽樣值ynew能夠進一步被用來建立其后續的優化指標函數。在給定的試驗數據data下,假設輸出響應的規格限為A,其模擬輸出響應ynew(x)落在其對應規格限A的貝葉斯后驗概率函數為

(17)

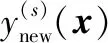
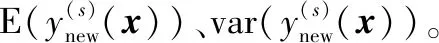
(18)

上述的最小均方誤差函數更多關注輸出響應與目標值之間的偏差,以及輸出響應的波動,即更多關注的是產品/過程的穩健性。在實際應用中,研究人員需要在最大化符合性概率與最小化均方誤差之間進行權衡。為此,本文提出了一種行之有效的優化策略,其具體的優化模型如下:

(19)

式中:p0代表所期望滿足的符合性概率,即產品或過程的合格率;L和U分別代表可控因子在試驗區域內的上界和下界。在滿足所期望的符合性概率的條件下,通過最小化均方誤差函數來實現產品或過程的穩健性,從而實現產品/過程的穩健參數設計。上述的目標函數和約束函數都是在輸出響應后驗樣本基礎之上構建獲得,因此其目標函數和約束函數均表現為高度復雜的非線性特征,傳統的優化方法(如線性規劃等)將難以獲得理想的優化結果。為此,本文將借鑒以往的研究經驗,利用混合遺傳算法對上述優化模型,即式(19),進行參數優化。

2.4 本文所提方法的實施步驟

針對非正態響應的穩健參數設計問題,本文提出了一種考慮噪聲因子的貝葉斯建模與穩健參數優化方法,其具體的實施步驟如下。

步驟 1在GLM框架下結合貝葉斯先驗信息考慮試驗設計的因子效應原則(如效應稀疏、效應排序、效應遺傳),從而篩選出顯著性因子效應。

步驟 2將所識別出的顯著性因子劃分為可控因子和噪聲因子,對所構建的貝葉斯響應曲面模型的參數賦予經驗貝葉斯先驗信息,從而利用Gibbs抽樣方法獲得模型參數的抽樣值。

步驟 3考慮產品制造或使用過程的實際情況,并根據歷史數據或經驗信息來確定噪聲因子的分布信息。在此基礎上進一步結合上述參數的迭代抽樣值,來更新GLM的均值函數,從而獲得考慮噪聲因子情形下的輸出響應模擬抽樣值。

步驟 4利用所獲得的輸出響應模擬抽樣值分別構建最小均方誤差函數和貝葉斯后驗概率函數,并將二者進行有機的結合,構建一種新的優化模型,即在滿足貝葉斯后驗概率大于預先設定的期望概率的情況下,最小化均方誤差。上述的優化策略不僅能夠關注產品或過程的符合性概率,也能夠有效地實現產品或過程的穩健性。

步驟 5利用混合遺傳算法對所構建的優化模型進行參數優化,從而獲得理想的參數設計值。在R軟件中,需要將式(19)約束優化問題轉化為一種考慮懲罰的適應度函數,然后對所構建的適應度函數進行優化,獲得最優的參數設計值。

3 實例分析

3.1 電阻率試驗

為了進一步驗證本文所提方法的有效性和可靠性,本文選擇某測試晶片的電阻率實驗[41]來加以說明和分析。在該電阻率實驗中,影響電阻率y變化的設計因子主要為:離子注入的劑量x1、時間x2、氧化層的厚度x3,以及溫度x4。研究人員旨在通過試驗設計方法來尋求影響某測試晶片電阻率的最佳參數設計值。為此,研究人員選擇全因子設計24開展相關的研究。考慮到在實際的應用中,溫度難以被控制,在此將其視為噪聲因子z,具體的實驗數據如表1所示。

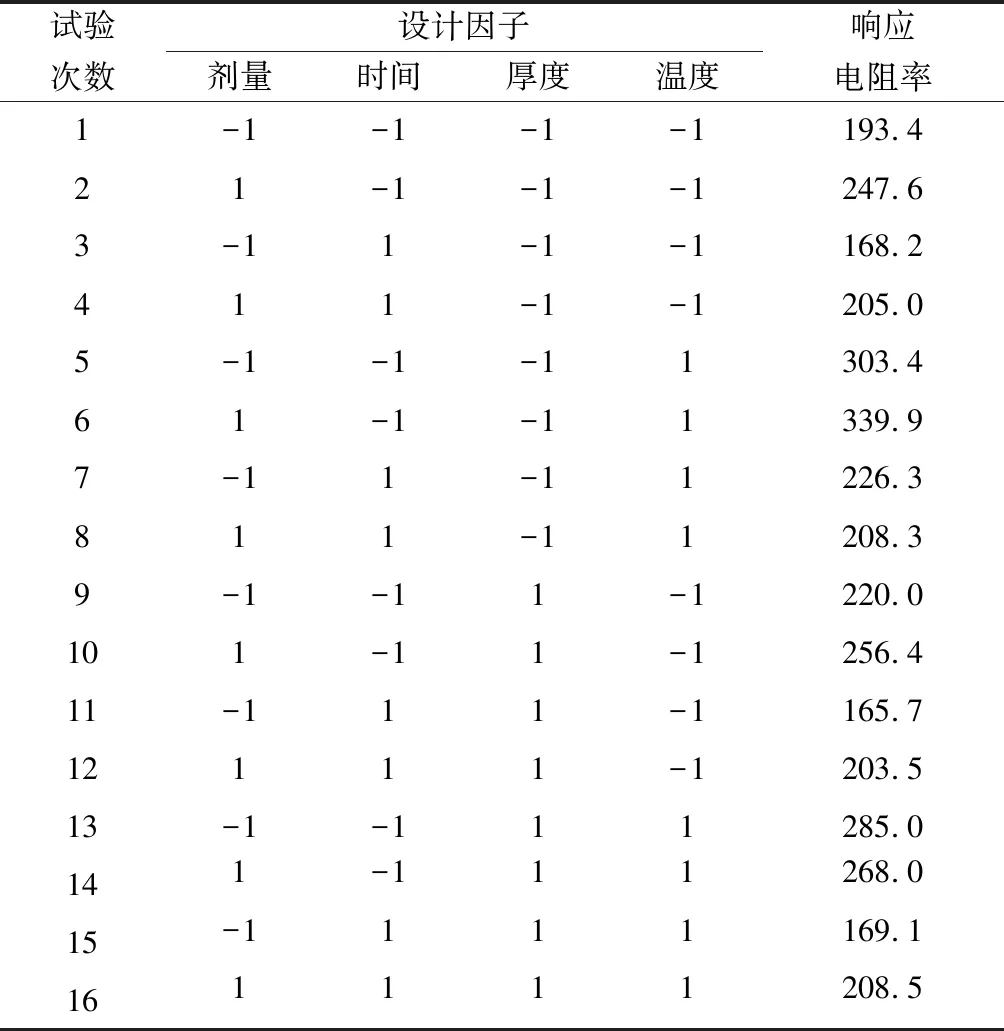
表1 電阻率試驗的研究結果

3.2 考慮因子效應原則的變量篩選

然后,由于對模型參數缺乏必要的先驗信息,在此假設模型參數的顯著性是等概率的,即假設式(7)的pj=0.5。在此基礎上,結合式(9)和式(10)計算出各模型參數所對應的變量指示器后驗概率值。根據變量指示器后驗概率的計算結果可知,因子效應的顯著性排序分別為:x2,x4,x1,x3x4,x2x4,x1x4,x3。遺傳效應原則是指若交互效應x3x4顯著,則所對應的主效應x3或x4至少有一個是顯著的。在貝葉斯變量選擇中,強遺傳效應與弱遺傳效應通常通過二階或高階交互效應所對應的變量指示器的先驗概率加以區分。例如,在強遺傳效應下,其二階交互效應所對應的變量指示器的先驗概率如果設置為0.3,則在弱遺傳效應原則下其所對應的變量指示器的先驗概率需要設置得更低一些,如0.1。需要指出的是,本文在設置變量指示器的先驗概率時,不僅考慮了因子效應原則,而且還利用經驗貝葉斯先驗方法考慮了以往研究方法的參數估計結果。由于本文所選的實際案例所涉及的主效應因子數目較少,且僅考慮了二階交互效應,因此在考慮因子效應原則時,希望通過強遺傳效應對可能顯著的交互效應設置較大的先驗概率,以保留更多的顯著性變量,從而方便與以往的研究方法進行對比和分析。根據因子效應遺傳原則和因子效應排序原則,若交互效應x3x4是顯著的,其主效應x3、x4往往也可被認為是顯著的。為此,需要重新調整一下顯著性因子的先驗信息,即假設pgamma1→c(1,1,1,1,0,0,0.3,0,0.3,0.3),利用式(10)重新計算可知顯著性因子的排序結果更新為:x2,x4,x1,x3,x3x4,x2x4,x1x4。上述的研究結果與以往文獻[11]的變量篩選結果存在較小的差別,但更加符合試驗設計的基本效應原則。

3.3 響應曲面建模與優化

4 討 論

4.1 噪聲因子波動對優化結果的影響

在產品或過程的穩健參數設計中,研究者始終關注的是如何通過選擇可控因子的最佳參數設計值,減少或控制噪聲因子對產品或過程波動的影響。因此,探討噪聲因子的波動變化對優化結果的影響,將有助于質量工程師或研究人員更為深刻地理解控制和減少噪聲因子的波動對實現產品或過程的穩健參數設計的重要意義。在第3.3節所獲得的最佳參數設計值下,通過改變噪聲因子的方差以反映噪聲因子的波動變化,進而分析了噪聲因子方差變化時其輸出響應的均方誤差和符合性概率的變化情況,其具體的研究結果如表2所示。

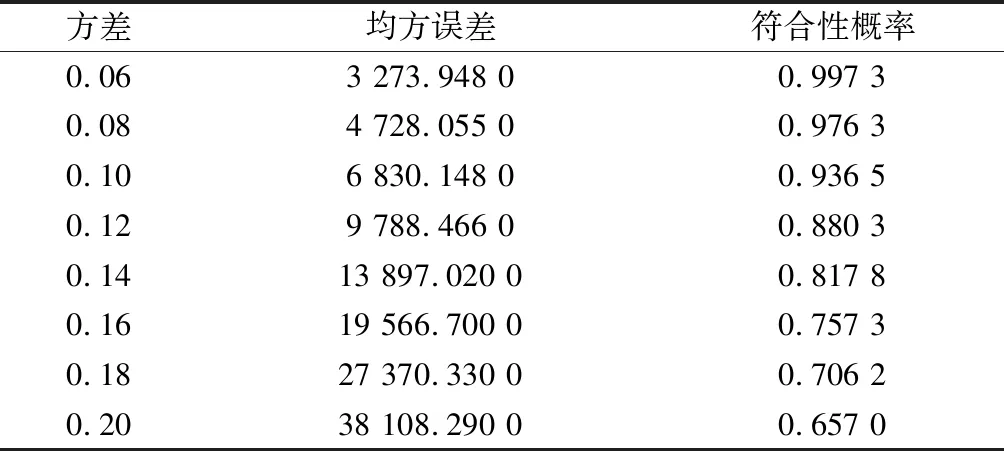
表2 噪聲因子方差變化對優化結果的影響

從表2可知,隨著噪聲因子的方差從0.06逐步增加到0.20,其均方誤差也逐步增大,同時其符合性概率則逐步減小。因此,在實現產品或過程的穩健參數設計時,需要收集噪聲因子變化的歷史數據信息或采用傳感器等新興技術在線獲取噪聲因子變化的信息,充分利用噪聲因子的變化信息以更好地提高產品或過程的穩健性和可靠性,從而提升產品或過程的質量設計水平。

4.2 不同研究方法的比較

在此,進一步考慮了因子遺傳效應原則(特別是強遺傳效應和弱遺傳效應)對優化結果的影響。為了比較在強遺傳效應和弱遺傳效應原則下所篩選出的顯著性變量差異對最終優化結果的影響,根據弱遺傳效應和以往研究的經驗信息,調整了主效應和交互效應的先驗信息,即pgamma1→c(1,1,0.5,1,0.1,0.1,0.3,0.1,0.3,0.1)。此時,利用式(10)重新計算其變量指示器的后驗概率,根據其研究結果可知,主效應x3的后驗概率將降低到0.062 9,因此在弱遺傳效應原則下,可將其視為非顯著性主效應,最終篩選出的顯著性效應為x1,x2,x4,x1x4,x2x4。在此基礎上,根據強、弱遺傳效應所識別出的顯著性變量的差異,利用本文所提方法對上述兩種情形下的優化結果進行比較,其優化結果如表3所示。此外,本文還考慮在滿足符合性概率不小于0.9的約束下,假設噪聲因子的波動方差為0.1、運用傳統的GLM進行非正態響應的穩健參數設計,其優化結果如表3所示。

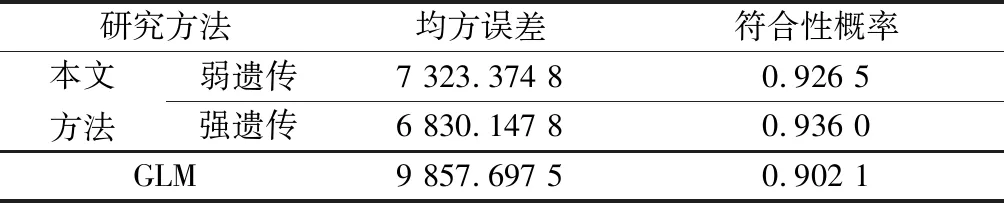
表3 不同研究方法的比較

從表3的研究結果可知,在強遺傳效應的作用下,所獲得的性能指標(如均方誤差和符合性概率)均表現更優。此外,無論是在弱遺傳效應或是強遺傳效應下,本文所提方法在性能指標上均要比不考慮因子效應原則的傳統GLM方法更為優越。需要特別指出的是,本文所提方法是建立在參數模擬抽樣基礎之上的,在實際應用中要注意對所獲取的參數抽樣值進行收斂性診斷,以確保根據其抽樣值所構建的優化指標的穩健性和可靠性。

5 結束語

針對非正態響應穩健參數設計問題,本文利用貝葉斯建模與抽樣技術構建了均方誤差函數和符合性概率函數,提出了一種考慮噪聲因子的穩健參數設計方法。案例研究結果也表明,噪聲因子的波動變化對優化結果具有非常顯著的影響,當噪聲因子的方差變大時,輸出響應的均方誤差會隨之變大,同時其符合性概率會隨之逐步變小。因此,在實際產品或過程的質量設計中,全面地了解和掌握噪聲因子的變化信息對提高產品或過程的質量設計水平是至關重要的。與以往方法比較而言,本文所提方法是在GLM的貝葉斯建模與優化框架下開展的相關研究工作,因此本文所提方法不僅適用于正態響應,也適用于更為廣泛的指數族分布類型,如常見的Gamma分布、泊松分布等響應類型。此外,本文所提方法不僅考慮了噪聲因子的波動變化對穩健參數設計優化結果的影響,而且還結合貝葉斯方法考慮了模型參數不確定性以及輸出響應波動對非正態響應穩健參數設計優化結果的影響。

伴隨著物聯網、傳感器技術的迅猛發展,在復雜產品或高端裝備的制造過程中對噪聲因子進行實時測量,然后利用統計與人工智能技術對所收集的質量數據進行分析已經成為當前亟待研究的重要課題,因此如何結合統計、大數據分析技術開展產品質量設計將是未來需要進一步深入研究的重要課題。