公理化模糊集合的特征及其分類
張 波, 潘小東, 謝健祥
(西南交通大學(xué) 數(shù)學(xué)學(xué)院, 四川 成都 611756)
Zadeh[1]在1965年引入了“模糊集合”的概念,旨在建立一種描述和處理模糊信息的數(shù)學(xué)理論和方法.模糊集合的基本思路是在絕對(duì)真(通常用1表示)和絕對(duì)假(通常用0表示)之間增加額外的真值來刻畫事物之間的差異所存在的中介過渡過程,即通過定義一個(gè)從非空論域U到[0,1](后來被推廣到格[2]、區(qū)間值[3]等其他結(jié)構(gòu))的函數(shù)(稱為隸屬函數(shù))來描述模糊概念(如:青年、高個(gè)子等)的外延.經(jīng)過50多年的研究與發(fā)展,模糊集合理論在理論與應(yīng)用2個(gè)方面都取得了長(zhǎng)足的進(jìn)步,目前已經(jīng)被廣泛應(yīng)用于諸如人工智能、聚類分析、模式識(shí)別、決策等領(lǐng)域[4-17].
對(duì)于模糊集合的理論和應(yīng)用而言,一個(gè)重要而基本的問題是:如何確定它的隸屬函數(shù)?對(duì)此,文獻(xiàn)[7]認(rèn)為:“模糊現(xiàn)象的特征是進(jìn)一步發(fā)展模糊邏輯及其應(yīng)用的根本……模糊現(xiàn)象在模糊邏輯的起源中扮演著關(guān)鍵角色.”文獻(xiàn)[8]認(rèn)為:“模糊性的本質(zhì)的研究是對(duì)人類智力的挑戰(zhàn).這方面的任何一點(diǎn)突破都將極大地推動(dòng)智能系統(tǒng)的研究,同時(shí)也將深化目前意義下的模糊性理論.”基于對(duì)模糊現(xiàn)象的深入分析,文獻(xiàn)[9]認(rèn)為:“模糊現(xiàn)象是反映事物的質(zhì)變和量變之間差異的一種現(xiàn)象,模糊性是在對(duì)事物進(jìn)行定性分析的時(shí)候,事物的質(zhì)和量之間所表現(xiàn)出來的差異特性.”基于這樣的認(rèn)識(shí),文獻(xiàn)[9]給出了隸屬度的公理系統(tǒng),并基于模糊劃分的概念給出了模糊集合的公理化定義.公理化模糊集合理論是對(duì)經(jīng)典模糊集合理論的嚴(yán)格化、明確化,這在一定程度上解決了模糊集合理論中長(zhǎng)期存在的關(guān)于隸屬函數(shù)的合理性問題,為模糊集合在理論和應(yīng)用方面的進(jìn)一步發(fā)展奠定了堅(jiān)實(shí)的理論基礎(chǔ).

1 預(yù)備知識(shí)
首先介紹文中使用到的一些記號(hào)以及三角模、三角余模和強(qiáng)否定算子.
定義 1.1[10]一個(gè)三角模(簡(jiǎn)稱t模)T指的是一個(gè)定義在[0,1]閉區(qū)間上的二元運(yùn)算T,即一個(gè)二元函數(shù)T:[0,1]2→[0,1],使得對(duì)任意的x,y,z∈[0,1],滿足以下4條公理:
(T1)T(x,y)=T(y,x);
(T2)T(T(x,y),z)=T(x,T(y,z));
(T3)T(x,y)≤T(x,z),當(dāng)y≤z;
(T4)T(x,1)=x.
定義 1.2[10]一個(gè)三角余模(簡(jiǎn)稱t余模)S指的是一個(gè)定義在[0,1]閉區(qū)間上的二元運(yùn)算S,即一個(gè)二元函數(shù)S:[0,1]2→[0,1],使得對(duì)任意的x,y,z∈[0,1],滿足(T1~T3)以及
(S4)S(x,0)=x.
本文中記三角模取小為?M,記三角余模取大為⊕M.
定義 1.3[11](否定、嚴(yán)格否定和強(qiáng)否定) (i) 稱一個(gè)不增的函數(shù)N:[0,1]→[0,1]為否定,如果:
(N1)N(0)=1,N(1)=0.
(ii) 稱一個(gè)否定N:[0,1]→[0,1]為嚴(yán)格否定,如果還滿足:
(N2)N是連續(xù)的.
(N3)N是嚴(yán)格單調(diào)遞減的.
(iii) 稱一個(gè)嚴(yán)格否定N:[0,1]→[0,1]為強(qiáng)否定,如果它還是對(duì)合的,即
(N4)N°N=id[0,1]是連續(xù)的.
顯然,N:[0,1]→[0,1]是一個(gè)嚴(yán)格否定當(dāng)且僅當(dāng)它是嚴(yán)格單調(diào)遞減的雙射.

定義 1.4[11](模糊劃分) 設(shè)U=[a,b]?R,U上的一個(gè)模糊劃分是具有如下形式的對(duì)象
其中
Ai={(x,μAi(x))|x∈U},i=1,2,…,n,
函數(shù)μAi:U→[0,1]定義了元素x∈U關(guān)于類Ai(代表某種質(zhì),即定性描述的類)的隸屬度,并且滿足下面的條件:
μAi(x0)=1;
μAi(x0)=1,
那么,μAi(x)在[a,x0]上不減,在[x0,b]上不增;
4) 對(duì)任意的x∈U,有
0<μA1(x)+μA2(x)+…+μAn(x)≤1.

基于模糊劃分,下面給出模糊集合的公理化定義.
定義 1.5[11](公理化模糊集合) 設(shè)

μA(x)=μAi(x)
對(duì)所有x∈U都成立,那么
2) 如果μA(x)=1對(duì)所有x∈U都成立,那么

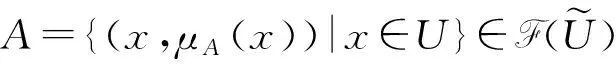
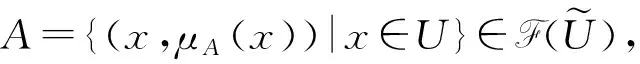

B1∩?B2∩?…∩?Bn∩?…=
B1∪⊕B2∪⊕…∪⊕Bn∪⊕…=



2 公理化模糊集合的規(guī)范形式

例如,在正則模糊劃分
下,取強(qiáng)否N為N(x)=1-x,設(shè)
B(x)=1-A2(x)=(A2(x))N,
雖然A1和B表面上并不相同,實(shí)際上卻是一致的.那么,在公理化模糊集中,怎么判斷表面上不一樣而實(shí)際上是相等的2個(gè)模糊集呢?
命題 2.1設(shè)
A={(x,μA(x))|x∈U},B={(x,μB(x))|x∈U}∈
則
(A∩?MB)r=Ar∩?MBr,(A∪⊕MB)r=Ar∪⊕MBr.
證明任取x∈U,若A(x)≥B(x),則
(A∩?MB)r(x)=
(A(x)?MB(x))r=(B(x))r.
又因?yàn)閞∈R+,故
(A(x))r≥(B(x))r,
那么
(Ar∩?MBr)(x)=
(A(x))r?M(B(x))r=(B(x))r,
故
(A∩?MB)r=Ar∩?MBr.
A(x) 采取相同的辦法可以證明∪⊕M與語(yǔ)氣算子也可交換,即 (A∪⊕MB)r=Ar∪⊕MBr. 因?yàn)槿⌒?M、取大⊕M之間是有分配律的,故∩?M、∪⊕M之間也有分配律,即下面命題成立. 命題 2.2設(shè) 則: (A∪⊕MB)∩?MC=(A∩?MC)∪⊕M(B∩?MC), (A∩?MB)∪⊕MC=(A∪⊕MC)∩?M(B∪⊕MC). 稱定義1.5中3)對(duì)應(yīng)的生成模糊集的方式為A經(jīng)過了一次語(yǔ)氣運(yùn)算. 定義 2.3由有限個(gè)簡(jiǎn)單模糊集構(gòu)成的模交式稱作模交模糊集,由有限個(gè)簡(jiǎn)單模糊集構(gòu)成的模并式稱作模并模糊集. A=(A1)N∩?(A2)2,B=A2∪⊕((A1)N)3, 則A是模交模糊集,B是模并模糊集. 定義 2.4由有限個(gè)模交模糊集構(gòu)成的模并式稱作模并模糊集范式,由有限個(gè)模并模糊集構(gòu)成的模交式稱作模交模糊集范式. A=(A1∩?(A2)2)∪⊕((A2)N∩?(A1)2),B=((A1)N∪⊕A2)∩?((A2)3∪⊕A1), 則A是模并模糊集范式,B是模交模糊集范式. 證明當(dāng)A=U或者A=?時(shí),規(guī)范形式已經(jīng)約定好,命題成立;否則,A是由模糊劃分中的元素生成的,此時(shí)可以按照如下的步驟找到A的規(guī)范形式.有以下恒等關(guān)系: (A∩?MB)r=Ar∩?MBr, (1) (A∪⊕MB)r=Ar∪⊕MBr, (2) (A∩?MB)N=AN∪⊕MBN, (3) (A∪⊕MB)N=AN∩?MBN, (4) (A∪⊕MB)∩?MC=(A∩?MC)∪⊕M(B∩?MC), (5) (A∩?MB)∪⊕MC= (A∪⊕MC)∩?M(B∪⊕MC). (6) 根據(jù)(1)~(6)式,可以按以下步驟找到定理中的模交模糊集范式和模并模糊集范式. 第1步 利用(1)~(4)式可以把模糊集A變換成B1,使得B1是由簡(jiǎn)單模糊集經(jīng)∪⊕M、∩?M運(yùn)算生成,并且A與B1是相等的. 第2步 根據(jù)(5)式可以把B1變換為B2,但B2中∩?M的作用范圍內(nèi)不出現(xiàn)∪⊕M,并且B2與B1相等,顯然B2就是定理中所要求的模并模糊集范式. 經(jīng)過類似于上述的步驟,但在第2步中使用(6)式,就得到定理中所要求的模交模糊集范式. A=((A1∩?MA2)3∪⊕MA3)N 的規(guī)范形式. 解使用(4)式得 A=((A1∩?MA2)3)N∩?M(A3)N, 使用(1)式得 A=((A1)3∩?M(A2)3)N∩?M(A3)N, 使用(3)式得 A=(((A1)3)N∪⊕M((A2)3)N)∩?M(A3)N, (7) 使用(5)式得 A=(((A1)3)N∩?M(A3)N)∪⊕M (((A2)3)N∩?M(A3)N). (8) (7)式為與模糊集A相等的模交模糊集范式,(8)式為與模糊集A相等的模并模糊集范式. 基于公理化模糊集合的規(guī)范形式,下面研究公理化模糊集合的特征和性質(zhì).由前面的定義可知下面的結(jié)論成立. 命題 3.11) 模并(交)模糊集范式在x0處的隸屬度為0(1),當(dāng)且僅當(dāng)構(gòu)成該模并(交)模糊集范式的每個(gè)模交(并)模糊集在x0處的隸屬度為0(1); 2) 模并(交)模糊集范式在x0處的隸屬度為1(0),當(dāng)且僅當(dāng)構(gòu)成該模并(交)模糊集范式的模交(并)模糊集中至少存在一個(gè)模交(并)模糊集,它在x0處的隸屬度為1(0); 3) 模交(并)模糊集在x0處的隸屬度為1(0),當(dāng)且僅當(dāng)構(gòu)成該模交(并)模糊集的每一個(gè)簡(jiǎn)單模糊集在x0處的隸屬度均為1(0); 4) 模交(并)模糊集在x0處隸屬度為0(1),當(dāng)且僅當(dāng)構(gòu)成該模交(并)模糊集的簡(jiǎn)單模糊集中至少存在一個(gè)簡(jiǎn)單模糊集,它在x0處隸屬度取值為0(1). 這里只證明1),其余的結(jié)論可類似說明. A=B1∪⊕MB2∪⊕M…∪⊕MBl,l∈N+, 其中Bi均為模交模糊集.若A(x0)=0,則 (B1∪⊕MB2∪⊕M…∪⊕MBl)(x0)=0, 即 B1(x0)⊕MB2(x0)⊕M…⊕MBl(x0)=0, 從而 B1(x0)=B2(x0)=…=Bl(x0)=0, 所以說它的每個(gè)模交模糊集在x0處取值為0.上述證明反過來也成立,從而原命題成立.A(x0)=1時(shí)類似可證. 證明因?yàn)锳是模交模糊集,所以設(shè) A=B1∩?MB2∩?M…∩?MBl,l∈N+, 其中Bi,i∈{1,2,…,l}是簡(jiǎn)單模糊集. 由模糊集核的定義可知Aj(x)=1,由模糊劃分定義1.4的條件4) 0<μA1(x)+μA2(x)+…+μAn(x)≤1, 可知 Ai(x)=0,i≠j, 所以模糊劃分中元素在x處取值為0或1;又因?yàn)锽i是簡(jiǎn)單模糊集,不妨假設(shè)Bi是由模糊劃分中元素Ak生成的,注意到Ak(x)=1或0.結(jié)合簡(jiǎn)單模糊集的定義可知,簡(jiǎn)單模糊集Bi(x)=0或1,i∈{1,2,…,l},從而 A(x)=B1(x)?MB2(x)?M…?MBl(x)=0或1. 證明考慮AN.因?yàn)锳是模并模糊集,則AN是模交模糊集.根據(jù)命題3.2可知AN(x)=0或1,由強(qiáng)否定的性質(zhì)知A(x)=(AN(x))N=1或0. 在這些結(jié)論的基礎(chǔ)之上可以得到下面的定理. 證明如果A=U或者?,結(jié)論顯然成立. 根據(jù)定理2.1,不妨設(shè) A=B1∪⊕MB2∪⊕M…∪⊕MBk,k∈N+, 其中Bi,i∈{1,2,…,k}均是模交模糊集. 由命題3.2知Bi(x0),i∈{1,2,…,k}取值為0或1,故 A(x0)=B1(x0)⊕MB2(x0)⊕M…⊕MBk(x0)=0或1. 容易發(fā)現(xiàn),若A∈C0,則AN∈C1;若B∈C1,則BN∈C0;若C∈C2,則CN∈C2.3類元素關(guān)于語(yǔ)氣算子均是封閉的.下面討論∩?M、∪⊕M下,3類元素的運(yùn)算問題,首先討論∩?M下同類模糊集之間的運(yùn)算. 1)A∩?MB∈C0,?A,B∈C0; 2)A∩?MB∈C1,?A,B∈C1; 3)A∩?MB?C1,?A,B∈C2. 證明1) 任取A,B∈C0,則 則 (A∩?MB)(x1)=A(x1)?MB(x1)=0?M0=0, 所以 A∩?MB∈C0. A(x1)=B(x1)=1, 那么 (A∩?MB)(x1)=A(x1)?MB(x1)=1?M1=1, 從而 A∩?MB∈C1. (A∩?MB)(x1)=A(x1)?MB(x1)= 0?MB(x1)=0, 從而 A∩?MB?C1. C2中任意元素與自身做∩?M運(yùn)算屬于C2.下面舉例說明C2與C2中元素做運(yùn)算可能屬于C0. 關(guān)于∩?M下不同類間元素的運(yùn)算,有如下結(jié)論. 1)A∩?MB∈C0,?A∈C0,B∈C1; 2)A∩?MB∈C0,?A∈C0,B∈C2; 3)A∩?MB∈C2,?A∈C1,B∈C2. 證明1) 任取A∈C0,B∈C1,則 都有 A(x0)=0,B(x0)=1, 那么 (A∩?MB)(x0)=A(x0)?MB(x0)=0?M1=0, 所以 A∩?MB∈C0. 2) 任取A∈C0,B∈C2,則對(duì) 都有A(x0)=0,那么 (A∩?MB)(x0)=A(x0)?MB(x0)= 0?MB(x0)=0, 所以 A∩?MB∈C0. B(x0)=1,B(x1)=0. 又因?yàn)锳∈C1,所以 A(x0)=A(x1)=1, 從而 (A∩?MB)(x0)=A(x0)?MB(x0)=1?M1=1,(A∩?MB)(x1)=A(x1)?MB(x1)=1?M0=0, 故A∩?MB∈C2. 類似地,關(guān)于∪⊕M運(yùn)算有如下性質(zhì). 1)A∪⊕MB∈C0,?A,B∈C0; 2)A∪⊕MB∈C1,?A,B∈C1; 3)A∪⊕MB?C0,?A,B∈C2. 證明1) 任取A,B∈C0,則AN,BN∈C1,那么由命題3.4中2)可知 (A∪⊕MB)N=AN∩?MBN∈C1, 從而A∪⊕MB=((A∪⊕MB)N)N∈C0. 2) 任取A,B∈C1,則AN,BN∈C0,那么由命題3.4中1)可知 (A∪⊕MB)N=AN∩?MBN∈C0, 從而A∪⊕MB=((A∪⊕MB)N)N∈C1. (A∪⊕MB)(x1)=A(x1)⊕MB(x1)= 1⊕MB(x1)=1, 從而A∪⊕MB?C0. 下面舉例說明C2與C2中元素做∪⊕M運(yùn)算可能屬于C1. {(x,(-x+1)⊕Mx|x∈U}∈C1. 1)A∪⊕MB∈C1,?A∈C0,B∈C1; 2)A∪⊕MB∈C2,?A∈C0,B∈C2; 3)A∪⊕MB∈C1,?A∈C1,B∈C2. 證明1) 任取A∈C0,B∈C1,則 AN∈C1,BN∈C0, 那么由命題3.5中1)可知 (A∪⊕MB)N=AN∩?MBN∈C0, 從而A∪⊕MB∈C1. 2) 任取A∈C0,B∈C2,則 AN∈C1,BN∈C2, 那么由命題3.5中3)可知 (A∪⊕MB)N=AN∩?MBN∈C2, 從而A∪⊕MB∈C2. 3) 任取A∈C1,B∈C2,則 AN∈C0,BN∈C2, 那么由命題3.5中2)可知 (A∪⊕MB)N=AN∩?MBN∈C0, 從而A∪⊕MB∈C1. 本文定義了公理化模糊集合的2種規(guī)范形式,證明了(N,?M,⊕M)型公理化模糊集合的規(guī)范形式存在定理.基于規(guī)范形式證明了(N,?M,⊕M)型公理化模糊集合中元素的特征,并給出了模糊集的 分類.這些成果對(duì)進(jìn)一步研究公理化模糊集合的數(shù)學(xué)性質(zhì)、模糊隸屬空間的結(jié)構(gòu)和性質(zhì)具有重要的理論和實(shí)踐意義.本文研究的是帶Zadeh算子和強(qiáng)否定算子的公理化模糊集合,一般情形下的公理化模糊集合的規(guī)范形式和特征還需要進(jìn)一步的研究;這將是今后努力的方向.





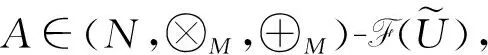

3 公理化模糊集合的特征及分類










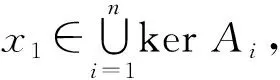




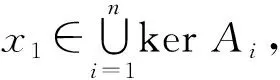


4 結(jié)束語(yǔ)

