高考中志在必得的復數(shù)題

焦婭瓊

(山東省淄博市張店區(qū)第一中學)

復數(shù)專題內(nèi)容是高考熱點,主要以選擇題或填空題的形式出現(xiàn),考查復數(shù)的概念、復數(shù)的四則運算、復數(shù)的模及復數(shù)的幾何意義等,難度較小.本文以2022年高考真題為例,分析總結(jié)復數(shù)的考查方向.

1 真題再現(xiàn)

真題1(2022年新高考Ⅰ卷2)若i(1－z)＝1,則＝( ).

A.－2 B.－1 C.1 D.2

真題2(2022年新高考Ⅱ卷2)(2＋2i)(1－2i)＝( ).

A.－2＋4i B.－2－4i

C.6＋2i D.6－2i

真題3(2022年全國甲卷理1)若z＝－1＋＝( ).

真題4(2022年全國甲卷文3)若,則＝( ).

由于z＝1＋i,故2－2i,則,故選D.

真題5(2022年全國乙卷理2)已知z＝1－2i,且,其中a,b為實數(shù),則( ).

A.a＝1,b＝－2 B.a＝－1,b＝2

C.a＝1,b＝2 D.a＝－1,－b＝2因為z＝1－2i,且z＋＋b＝0,所以(1－2i)＋a(1＋2i)＋b＝(1＋a＋b)＋(－2＋2a)i＝0,所以得a＝1,b＝－2,故選A.

真題6(2022年全國乙卷文2)設(shè)(1＋2i)a＋b＝2i,其中a,b為實數(shù),則( ).

A.a＝1,b＝－1 B.a＝1,b＝1

C.a＝－1,b＝1 D.a＝－1,b＝－1

2 回歸課本

回歸到課本中,復數(shù)專題主要有以下幾個考點.

考點1考查復數(shù)的概念.如表1所示,處理復數(shù)概念問題時,一般采用定義法解決.

表1

基本方法將復數(shù)問題實數(shù)化,這是解決復數(shù)問題最基本的思想方法.

考點2考查復數(shù)的運算.如表2所示,在處理復數(shù)四則運算問題時,一般按照運算法則進行,應(yīng)加強數(shù)據(jù)處理能力的訓練.

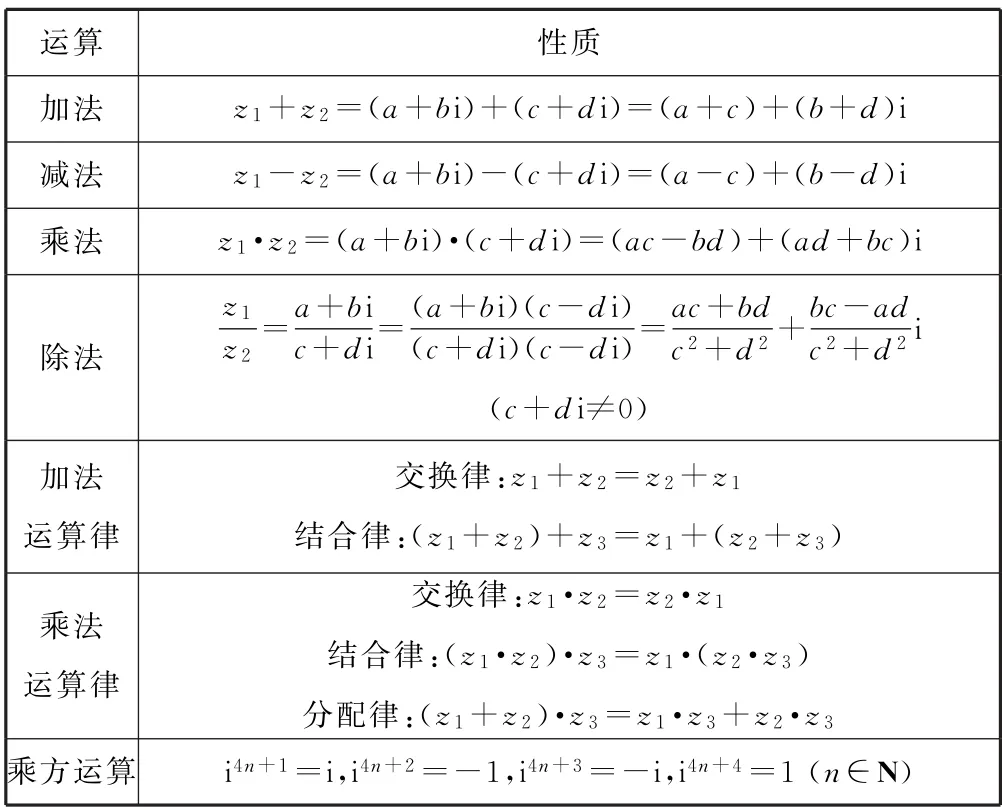
表2

基本方法先把復數(shù)z用復數(shù)的代數(shù)形式表示出來,再用待定系數(shù)法求解,這是解決復數(shù)運算問題的基本方法.

考點3考查復數(shù)的幾何意義如表3所示.

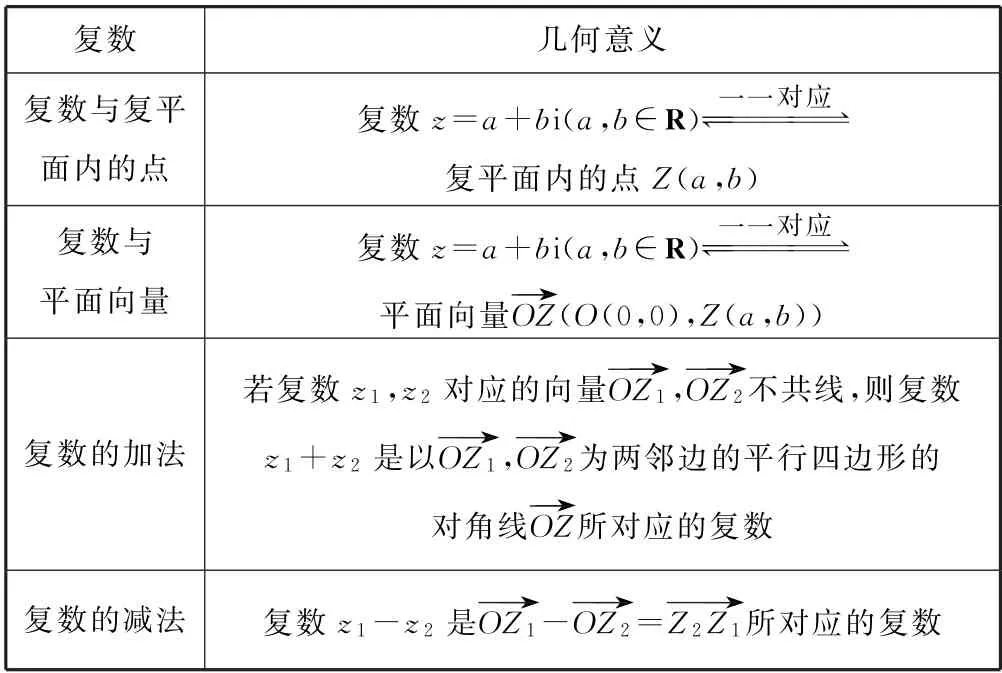
表3

3 創(chuàng)新模擬

4 拓展延伸

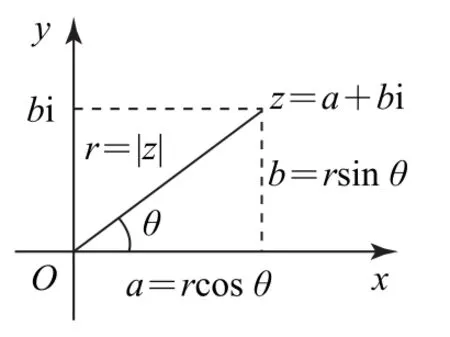
圖1

復數(shù)乘、除運算的三角表示:已知復數(shù)z1＝r1(cosθ1＋isinθ1),z2＝r2(cosθ2＋isinθ2),則

5 綜合評價

從近幾年高考情況來看,考查的重點仍是復數(shù)的四則運算,也兼顧考查復數(shù)的幾何意義、求模、共軛復數(shù)等基本知識,既屬于簡單題,也屬于易錯題.對于綜合創(chuàng)新的考查形式,求解瓶頸是“轉(zhuǎn)化”,在充分理解題意的基礎(chǔ)上化“生”為“熟”,考試中力求快、準、穩(wěn).

(完)