基于徐變損傷理論的早齡期大體積混凝土化學-熱-力多場耦合模型研究

王 晴，任曉丹

(同濟大學土木工程學院，土木工程防災國家重點實驗室，上海 200092)

混凝土澆筑完成后的最初幾天是混凝土劇烈變形和性能提升的關鍵時期。在早齡期養護過程中，水泥的水化作用：一方面會引起材料體積變化，產生自收縮變形；另一方面，水化反應會不斷釋放熱量，使得混凝土內部發生溫度變化，并引起溫度變形。受自收縮變形、溫度變形以及周圍約束作用的影響，早齡期混凝土結構，尤其是大體積混凝土，極易產生較大的內力作用。在這一過程中，混凝土的徐變效應也會影響其內力狀態。與成熟混凝土相比，早齡期混凝土的強度等力學性能相對較低，上述內力、變形作用可能會使結構在早齡期階段發生損傷、開裂等不利行為[1]。

早齡期混凝土的開裂行為會加速鋼筋的銹蝕、碳化等有害化學反應，嚴重影響鋼筋混凝土結構的長期承載力，給工程結構全壽命周期的安全性埋下了隱患；對于一些具有抗滲防滲要求的結構，如橋梁隧道、混凝土路面、混凝土大壩等，早齡期階段的變形、應力作用以及開裂行為，會對結構的功能性產生不利的影響[2]。另外，對于一些具有密閉性要求的結構，如核電站安全殼、液化天然氣儲罐等，早齡期的開裂行為可能會引起核物質、可燃性氣體等的泄露問題，甚至造成災難性的工程事故。由此可見，開展早齡期混凝土的力學行為研究，綜合反映混凝土早齡期階段的開裂、徐變、溫度變形、自收縮變形和齡期效應等各項力學行為，對于保證工程結構全壽命周期的安全性和耐久性具有重要意義。

從力學的角度考察，早齡期大體積混凝土的行為涉及到多場耦合作用、徐變效應和損傷發展。其中，多場耦合作用是指在早齡期階段，大體積混凝土至少包含應力-變形場、溫度場和化學場的作用，其中，化學場與放熱過程密切相關，將會引起溫度場變化，溫度場會影響應力-變形場。徐變則是指混凝土在長期的應力作用下產生的持續變形，且變形量同時受到溫度和水化反應程度的影響。而損傷是指混凝土在應力、溫度等的共同作用下會產生開裂現象，并伴隨著材料性能的劣化。

混凝土多場耦合模型的研究歷史并不長，20世紀90年代ULM 等[3-4]發展了一類化學-熱-力多場耦合模型，該模型綜合考慮了早齡期混凝土的溫度變化、塑性變形和齡期效應。后來，LACKNER 等[5]提出了化學-力兩場耦合模型，引入了Rankine 斷裂準則描述混凝土的受拉破壞行為，并成功應用于實際的碾壓混凝土壩結構。基于編制的早齡期子程序，我國學者王麗娟等[6-7]開展了混凝土路面板結構早齡期翹曲的數值模擬研究，綜合考慮了溫度場、濕度場和徐變行為的影響。上述模型植根于塑性力學理論框架內，無法反映由于損傷發展引起的混凝土強度軟化、剛度退化等行為[8]。另外，ULM 等[3-4]和LACKNER等[5]的研究也沒有考慮到混凝土徐變變形的影響。

混凝土徐變的研究由來已久，我國學者在此方面開展了系統的研究工作。20世紀五六十年代，趙祖武[9]建立了混凝土非線性徐變的基本表達，合理考慮了齡期效應、彈性后效等特征。朱伯芳[10]將混凝土徐變行為引入了大體積混凝土研究中，分析了徐變影響下拱壩的內力重分布，通過理論推導得到了靜荷載和溫度作用下壩體應力的具體解答，極大地促進了混凝土拱壩結構的發展。黃海東等[11]提出一類混凝土非線性徐變模型，結合顯式迭代方法，實現了對長期持荷作用下混凝土裂縫擴展過程的模擬。然而，上述研究成果均忽略了環境變化等因素的影響。此后，為了考慮多重因素對徐變變形的影響，美國學者BA?ANT等[12- 13]從材料微觀角度研究混凝土的徐變變形，提出了微觀應力-固化理論，該模型綜合考慮了齡期效應、溫濕度變化對徐變變形的影響，具有較為堅實的理論基礎。目前，混凝土徐變變形的研究已經趨于成熟，相關研究成果也已經寫入設計規范[14- 16]之中。

近年來，損傷力學理論蓬勃發展，損傷的概念在物理本質上契合了混凝土典型的應變軟化、剛度退化等特征[8]，并且具有較高的數值計算效率。20世紀90年代，CERVERA 等[17- 18]將連續介質損傷理論、微觀應力-固化理論與多孔介質理論相結合，發展了早齡期混凝土的化學-熱-力學分析模型，考慮了早齡期混凝土的水化反應、齡期效應、損傷發展和徐變效應。但是，CERVERA等[17- 18]的模型在徐變行為分析過程中并未考慮環境條件的影響。為了更為合理地描述早齡期混凝土的氣、液和固相的耦合影響，GAW IN 等[19-20]將混凝土視為一種多孔多相粘彈性材料，綜合考慮了早齡期階段的氣-液相變、濕-熱耦合效應和齡期效應，并在徐變演化過程中引入了非線性函數以反映微裂縫發展引起的徐變放大效應。該模型雖然合理考慮了損傷引起的非線性徐變行為，但是在本質上仍屬于彈塑性模型，對混凝土損傷開裂過程的描述較為不足。而后，HILAIRE 等[21]、GASCH等[22]、金賢玉等[23]和吳建營等[24]學者相繼開展了相關研究工作。綜合來看，早齡期混凝土的損傷分析框架已經引起了學術界和工程界的關注，但由于早齡期混凝土力學行為的復雜性，目前已有的研究工作對早齡期大體積混凝土力學行為的考慮尚不夠全面，無法綜合地考慮早齡期混凝土的各項變形特征，分析結果也不能滿足理論分析和工程應用的需要。

針對上述問題，本文提出了一類適用于早齡期大體積混凝土的化學-熱-力多場耦合模型。該模型將水化反應方程與熱傳導方程耦合考慮以刻畫水化反應進程和溫度變化情況，結合彈塑性損傷理論和考慮損傷影響的微觀應力-固化理論，綜合地考慮了早齡期混凝土的損傷、徐變、溫度變形、自收縮變形和齡期效應，進一步建立了相應的顯式求解算法。在此基礎上，利用單軸試驗標定后的模型參數，對Maridal涵洞的“墻體-基礎”部分開展了精細化數值模擬研究，并考察了混凝土徐變變形的影響。計算結果表明，本文模型可以較好地預測早齡期階段大體積混凝土結構的開裂行為，為早齡期混凝土力學行為的研究提供了重要參考。

1 早齡期大體積混凝土化學-熱-力多場耦合模型

1.1 化學-熱場耦合作用模型

對于早齡期階段的大體積混凝土：一方面，混凝土的水化反應是一個放熱反應，并伴隨著材料力學性能的增強；另一方面，混凝土通過熱傳遞方式與外界環境發生熱量傳輸，會引起溫度變化并導致溫度變形，整個過程涉及化學場、溫度場和力場三個物理場的耦合，如圖1所示。因此，準確評估混凝土早齡期階段的力學行為需要合理反映水化反應進程和溫度場的變化。

圖1 早齡期混凝土的力學行為特征Fig.1 Early-age behavior of concrete

1.1.1水化反應模型

混凝土的水化反應是一個復雜的物理化學過程，準確描述水化反應進程需要建立完整的水化反應方程，求解過程繁瑣冗長，不利于與混凝土力學理論的耦合實現。為簡化考慮，這里采用ULM等[3]提出的唯象水化模型。引入水化度來刻畫水化反應進程，定義為當前累積水化生熱量與總的水化生熱量的比值，即：

根據JENDELE 等[25]的研究，水化度的演化速率可表示為：

式 中：Qξ為 活 化 能，取 為240.5 J·mol-1；R=8.3144 J·mol-1K-1為理想氣體常數；T/K 為當前溫度；Tref為參考溫度，取為2 93K ；為驅動水化反應的化學親和作用；B1、B2和η 為控制水化反應速率的模型參數； ξ∞為最終水化度，滿足[13]：

其中，w/c為混凝土的水灰比。雖然上述水化模型是一種簡化的、唯象的處理方法，但是相關研究[3]表明：這種方法可以兼顧計算效率與計算精度的要求，可以應用于早齡期大體積混凝土的力學行為模擬之中。

1.1.2熱傳導模型

早齡期混凝土的熱量傳輸過程采用如下的能量守恒方程進行描述：

式中： ρ為材料密度；Cp為比熱容；q為熱流通量，表示為：

式中， λt為熱傳導系數。需要指出的是，上述能量守恒方程中假定熱傳導過程是大體積混凝土早齡期階段主要的熱量傳輸方式，并引入了水化生熱項來刻畫水化放熱效應。

在結構熱邊界上滿足牛頓冷卻定律，表達式如下：

式中：BT為對流換熱系數；n為熱邊界上的單位法向量；Text為外界環境溫度。

1.2 混凝土徐變損傷模型

1.2.1應力-應變本構關系

基于小應變可疊加性，可將總應變張量 ε分解為彈性應變 εe、瞬時塑性應變 εp、徐變應變 εc、自收縮應變 εau和熱膨脹應變 εth之和，即：

為了描述混凝土開裂引起的材料軟化效應，這里采用吳建營等[26- 27]提出的彈塑性損傷模型，混凝土的本構關系可以表示為：

式中， E0為四階初始彈性剛度張量。

考慮到混凝土在拉、壓應力作用表現出截然不同的變形特征，可分別將名義應力 σ和有效應力進行如下的正負分解：

為了反映混凝土在拉、壓應力作用下迥異的剛度退化機制，分別在受拉、受壓應力空間引入受拉損傷變量d+和受壓損傷變量d-，此時，四階損傷張量 D可以進一步化簡為：

式中，P+和P-為正、負投影算子，具體表達見文獻[26]。對于損傷變量的演化，一般采用如下表達：

式中：上標符號 ±對應于受拉分量 +和受壓分量 -；r±為損傷閾值，即歷史最大的能量等效應變εeq±；g±(·)為損傷演化函數，可以通過單軸試驗方法或理論分析手段確定，這里采用吳建營等[27]提出的經驗損傷演化公式。

1.2.2瞬時塑性應變

對于大體積混凝土結構，直接基于經典塑性理論建立塑性演化關系一般需要多次迭代求解，計算量較大。為了提高數值分析的運算效率，這里采用了任曉丹等[28]提出的經驗塑性演化模型。將瞬時塑性應變張量 εp進行拉、壓分解，可得：

其中，受拉塑性應變 εp+和受壓塑性應變 εp-可表示為：

式 中：H(·)為 Heaviside 函 數；和為 模 型 參數，本文取=0.1 ，=0 ，=0.4。需要指出的是，式(16)認為混凝土的損傷演化驅動塑性演化，反映了損傷與塑性之間的耦合效應。

1.2.3徐變應變

在長期荷載作用下，混凝土表現出典型的徐變特征，即變形隨著持荷時間不斷增加。這里采用BA?ANT 等[13,29- 30]提出的微觀應力-固化理論進行描述。微觀應力-固化理論由固化理論和微觀應力理論兩個部分組成，其中，固化理論認為混凝土材料的短期徐變效應主要與水化反應有關，在澆筑完成后，混凝土內部仍然存在大量未水化水泥顆粒，隨著齡期的增加，未水化的水泥顆粒逐漸發生水化，材料性質不斷強化，從而引起徐變速率的降低。微觀應力理論則認為混凝土的長期徐變效應與微觀應力的釋放有關，BA?ANT等[29- 30]認為混凝土在微觀尺度上作用著一種自平衡的微觀應力，在長期持荷過程中，徐變變形增量會隨著微觀應力的釋放而不斷減小。由于其堅實的物理基礎，上述微觀應力-固化理論已被廣泛應用于混凝土的徐變變形分析之中[31-33]。

微觀應力-固化理論將徐變應變 εc分解為粘彈性應變項 εv和粘性流動應變項 εf兩個部分。其中，粘彈性應變項 εv由固化理論描述，滿足如下形式：

式中：q2、q3和k均為模型參數，k取為0.1；t為當前時間；t-t0為持荷時間。考慮到溫度升高會加速水化反應進程，進而引起徐變速率減小，式(18)引入了溫度影響時間tT(t)來刻畫溫度變化對粘彈性應變項的影響，滿足如下的Arrhenius定律：

式中，Qh為與水化過程有關的活化能，取為601.4 J·mol-1。Q(t-t0)為持荷時間(t-t0)和等效時間θ 的函數，可表示為：

其中，λ0=1 d，m=0.5；等效時間 θ 為 水化度 ξ的函數，取為：

粘性流動應變 εf表征了徐變變形中的不可恢復變形分量，根據微觀應力理論的相關研究[12,30]，粘性流動應變率可表示為：

其中，有效粘性系數 ηM為溫度T、相對濕度h與微觀應力S的函數，滿足如下表達：

其中，a和b均 為水化度 ξ 的函數，表征了水化程度對有效粘性系數 ηM的影響，表示為a=a0ξ∞/ξ和b=b0ξ∞/ξ，a0和b0均 與 材 料 參 數q4有 關，取 為a0=0.005q4和b0=0.00125q4。

微觀應力是一種作用于微觀孔隙上的橫向作用力，通常在水泥漿凝結硬化階段形成。根據等[1]的研究，將初始微觀應力S0取為：

其中，c0和q4均為材料參數。

微觀應力S由如下麥克斯韋型流變模型描述，即：

其中，Fq=1.6/q4，cs=22.5q4和ch=0.035；溫度相關參數 βη(T,h) 和 βC(T,h)分別表示為：

其中，Qη和QC為控制微觀應力演化的活化能，分別取為Qη=481.1 J·mol-1和QC=240.5 J·mol-1；p0=0.5，h*=0.75，nh=2.0。需要說明的是，本文假定混凝土的徐變變形發生在無損材料空間，因此，式(18)和式(23)中采用的應力表達均為有效應力張量。

相關試驗研究表明混凝土試件在受拉和受壓狀態下的徐變行為存在一定的差異[34]。類比損傷變量的正負分解，這里進一步對徐變應變進行拉壓分解，即：

混凝土的徐變變形與應力水平密切相關[34]。在早齡期階段，受溫度變形和自收縮變形的影響，大體積混凝土會在局部位置產生較大的內力，材料可能會從線性徐變階段進入非線性徐變階段。然而，上述微觀應力-固化理論是建立在線性徐變假設的基礎之上的。混凝土的非線性徐變行為本質上是損傷與徐變耦合作用的結果，為了綜合考慮混凝土的線性徐變與非線性徐變，本文引入了損傷影響函數h±(·)來刻畫由于損傷發展引起的非線性徐變行為[35]，h±(·)可表示為：

需要說明的是，當應力水平較小時，損傷基本不發展，此時h±(·)≈1，式(31)退化為經典的微觀應力-固化理論；隨著應力水平的提高，混凝土的損傷開始出現并不斷發展，材料進入非線性徐變階段，此時h±(·)＞1，式(31)中的徐變變形顯著增加。

另外，在長期持荷過程中，微觀應力-固化理論假定混凝土的彈性應變不隨齡期的變化而變化，這里對有效應力-彈性應變關系進行如下調整：

1.2.4自收縮應變與熱膨脹應變

為簡化考慮，這里假定混凝土的自收縮應變與水化度滿足線性關系，即：

式中：kau為比例系數；I為 二階單位張量； ξ0為水化度閾值[36]，取為ξ0=0.1，當水化度 ξ 超 過 ξ0后，混凝土開始出現自收縮變形。

式中，kth為熱膨脹系數。

1.2.5齡期效應

隨著水化反應的進行，混凝土材料表現出齡期效應，即宏觀力學性能隨著齡期不斷提高，在早齡期階段表現尤為顯著。為了考慮齡期效應的影響，下面分別從混凝土的剛度、強度和峰值應變三個方面展開討論。

如前所述，固化理論認為由于水化反應的影響，混凝土內水化產物的體積不斷增加并導致徐變變形速率的降低，也即材料的剛度特性隨著齡期的增加而提高。因此，這里不再重復考慮混凝土剛度的齡期效應。

對于強度的齡期效應，這里假定混凝土的抗拉強度ft和 抗壓強度fc與水化度ξ 滿足如下函數關系[37]：

式中：ft∞和fc∞為 ξ=ξ∞時的抗拉強度和抗壓強度； α 和 β均 為材料參數，本文統一取為α =0.5和β=0.9 ；為名義水化度，表示為：

一般來說，混凝土的峰值應變與強度成正比，與彈性模量成反比。結合式(35)，峰值拉應變 εt和 峰值壓應變 εc可表示為：

式中：E為與齡期無關的彈性模量，不隨著齡期的增加而變化； εt∞和 εc∞為ξ =ξ∞時的峰值拉應變和峰值壓應變。

2 模型數值實現

2.1 模型參數標定

上述早齡期混凝土多場耦合模型中的待定參數可劃分為化學-熱相關參數和力學相關參數兩大類。對于化學-熱相關參數，活化能Qξ、理想氣體常數R和參考溫度Tref均為模型常數，具體取值已在1.1小節中給出；普通混凝土的比熱容Cp、熱傳導系數 λT和 熱膨脹系數kau均可視為定值，可以直接根據已有的試驗資料確定；對流換熱系數BT一般需要結合混凝土外表面的傳熱性質進行標定；水化放熱參數(B1,B2,η,Lmax)和 自收縮系數kth均與混凝土的配合比密切相關，其中，自收縮系數kth可以根據早齡期混凝土的自收縮試驗確定，水化放熱參數(B1,B2,η,Lmax)則需要通過早齡期混凝土的水化放熱試驗進行標定。

對于力學相關模型參數，強度參數(E28,ft28,fc28)可以直接根據混凝土的強度等級或者實測的應力-應變曲線進行標定；徐變參數(c0,p1,p2,p3,p4)則需要通過不同齡期的徐變試驗結果進行標定；塑性參數(,)、其他徐變參數(λ0,m,k,a0,b0,Qη,QC,p0,h*,nh,,)以及齡期效應參數(α,β,ξ0)均可視為模型常數，建議取值已在1.2小節中給出。

2.2 模型數值求解算法

針對上述早齡期混凝土多場耦合模型，本文提出了一類顯式求解算法。由第1節的討論可知，混凝土的水化反應和熱量傳輸過程不受混凝土應力狀態影響，但水化程度和溫度變化會直接影響材料損傷的發展，另外，混凝土開裂過程的時間尺度遠小于化學-熱耦合過程[24]，因此，這里將多場耦合問題分解為化學-熱耦合求解與力學求解兩個串行子步驟，下面依次展開介紹。

問題：給定Δtn=tn+1-tn上 的應變增量Δ εn，且第n個 時 間 步tn上 的 各 個 狀 態 變 量{ξn,Tn,σn,均已知；

求解：更新第n+1個 時間步tn+1上的各個狀態變量

1)化學-熱耦合求解

熱量傳輸過程的控制方程本質上是一階擴散方程，其數值求解可以直接借助商用有限元軟件中的溫度求解模塊，進一步補充水化反應的求解過程，從而不斷更新早齡期混凝土的溫度場Tn+1和 水化度 ξn+1。

2)力學求解

借鑒算子分離方法[38]的基本思想，這里將早齡期混凝土的力學求解過程分為彈性試探、損傷修正、塑性修正和徐變修正四個步驟。

●彈性試探

首先根據 ξn+1和Tn+1，更新自收縮應變和熱膨脹應變，并計算彈性試探應力：

●損傷修正

●塑性修正

由式(16)可知，塑性應變增量Δ εp±是損傷變量d±和彈性應變增量Δ εe±的函數。為簡化計算，這里直接更新塑性應力增量 Δ σp±，即：

●徐變修正

徐變應變是由粘彈性應變分量和粘性流動分量組成。首先，由式(18)更新粘彈性應變分量：

利用式(26)確定微觀應力Sn+1，根據式(23)計算粘性流動應變增量Δεf:

然后，利用式(31)，更新第n+1個時間步tn+1上 的徐變應變，即：

相應地，將名義應力σn+1更新為：

至此，第n+1個 時間步tn+1上的各個狀態變量已經全部更新完成。上述顯式求解算法將早齡期混凝土的多場耦合問題分解為兩個串行子問題，整個求解過程無需迭代運算，具有較高的運算效率。

根據任曉丹等[28,39]的研究可知，上述顯式算法的穩定時間步長可表示為：

式中：αnon表征了由于材料非線性引起的計算失穩效應，建議取為0.80≤αnon≤0.98；ωmax為有限元模型的最大固有頻率；le和ce分別為單元e的特征長度和波速。

3 模型驗證與應用—以Maridal 涵洞為例

利用前述建立的早齡期混凝土多場耦合模型，本節將對文獻[40]中的Maridal 涵洞結構早齡期試驗進行精細化模擬，分析大體積混凝土在早齡期階段的受力性能和開裂行為。

3.1 有限元模型介紹

Maridal 涵洞結構是挪威首都奧斯陸城市環路的一個組成部分，全長約340 m。考慮到實際施工過程中采用分段澆筑，每段長15m，這里選取其中一段“墻體-基礎”結構進行有限元模擬。如圖2所示，該“墻體-基礎”結構總長15m，由墻體和基礎兩個部分組成，采用三維實體單元進行模擬。在澆筑過程中，基礎部分的澆筑先于墻體部分，在進行墻體澆筑時，基礎部分的混凝土已經達到預設強度要求，因此，這里只考慮墻體部分水化反應的影響，假定基礎部分為成熟混凝土，其水化反應速率很小可以忽略。

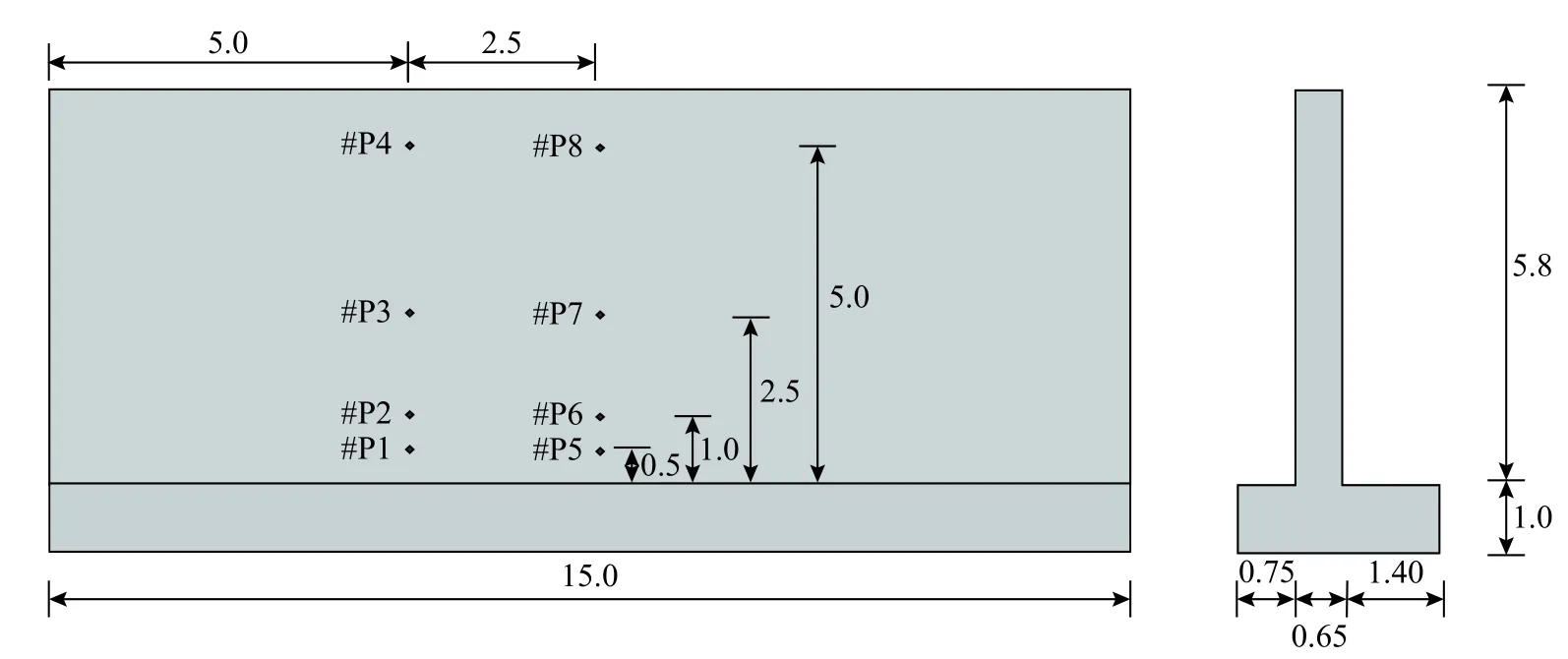
圖2 “墻體-基礎”結構示意圖/m Fig.2 Schematic diagram of the wall-foundation structure

3.2 模型驗證

為了識別混凝土的相關材料參數，挪威科技大學對與Maridal 涵洞結構同配合比的混凝土進行了一系列的單軸試驗，混凝土的配合比情況如下表1所示。本小節將利用相關單軸試驗結果進行模型參數的標定。除特殊說明外，數值模擬均采用圖3所示的棱柱體試塊，底部固定，上端自由，試件由一個單元組成。

表1 混凝土配合比Table1 Concrete composition

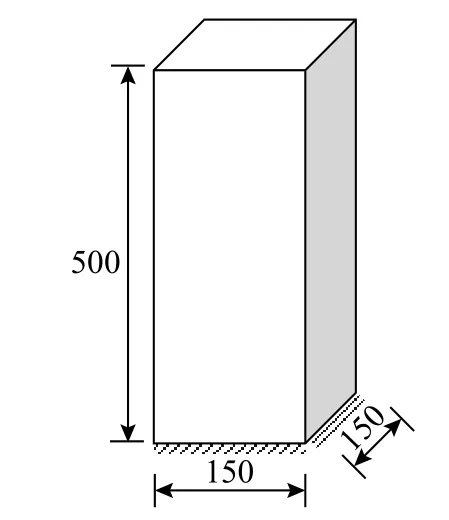
圖3 棱柱體試件示意圖/mm Fig.3 Schematic diagram of prism specimen

首先根據文獻[40]中的半絕熱試驗，對混凝土的化學-熱相關模型參數進行標定。試驗過程中外界環境溫度恒定為20℃。當水化反應相關模型參數取為B1=24.0 d-1，B2=1×10-5和η=8.0時，數值模擬中的化學親和作用演化曲線如圖4所示。當熱相關模型參數取為Lmax=231 150 kJ·m-3時，數值模擬得到的水化熱演化曲線與試驗結果的對比情況如圖5所示。可以看出，由于混凝土材料隨機性的影響，試驗實測的累積水化熱演化曲線表現出一定的離散性，數值模擬結果在試驗結果包絡范圍內，并與試驗結果表現出相似的變化趨勢。具體來說，在初始階段(0 h～50 h)，混凝土的水化反應較為劇烈，釋放的熱量較多從而導致水化熱曲線迅速上升；隨著齡期的增加，水化反應速率逐漸減小，釋放的熱量也隨之減小，對應的水化熱曲線也逐漸趨于平緩。

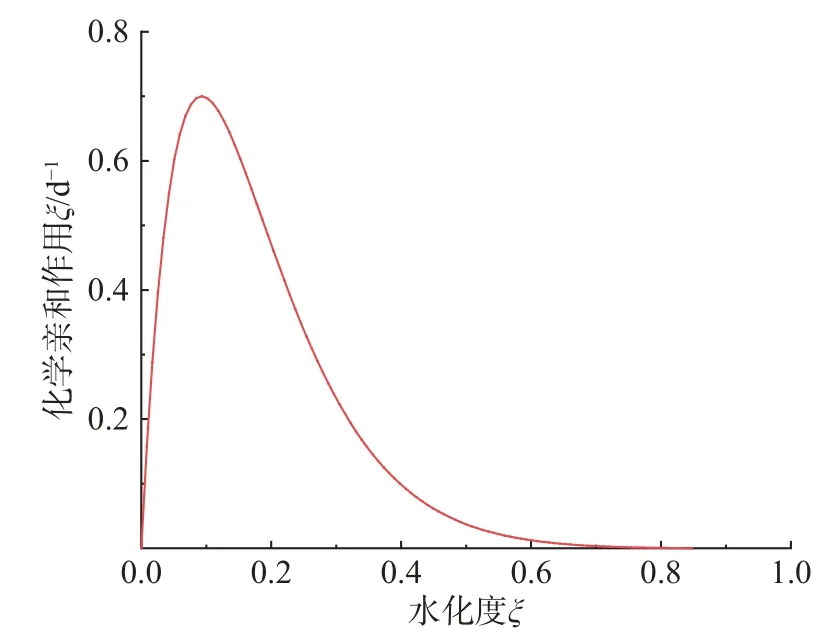
圖4 化學親和作用演化曲線Fig.4 Evolution curve of chem ical affinity

圖5 水化熱演化曲線Fig.5 Evolution curve of hydration heat

根據文獻[40- 41]中的抗壓強度試驗和劈裂抗拉試驗，對混凝土的強度模型參數進行標定。當28 d 抗壓強度和抗拉強度分別取為fc28=76MPa和ft28=4.3MPa時，計算結果與試驗結果的對比情況如圖6所示。其中，圖6(a)給出了數值模擬得到的抗壓強度演化曲線與試驗的對比情況。可以看出，計算結果與試驗結果吻合較好。圖6(b)給出了抗拉強度演化時程曲線的對比結果。由于試驗數據較少，圖中給出了兩組劈裂試驗結果，其中，“恒溫試驗”組代表在試驗室恒溫20℃條件下測得的抗拉強度結果；“現場試驗”組代表在Maridal涵洞現場進行試驗測得的結果，可以看出，數值模擬結果與“恒溫試驗”組結果吻合較好。與“恒溫試驗”組相比，“現場試驗”組結果的離散性較大，這主要是由現場試驗過程中外部環境溫度變化的隨機性引起的。

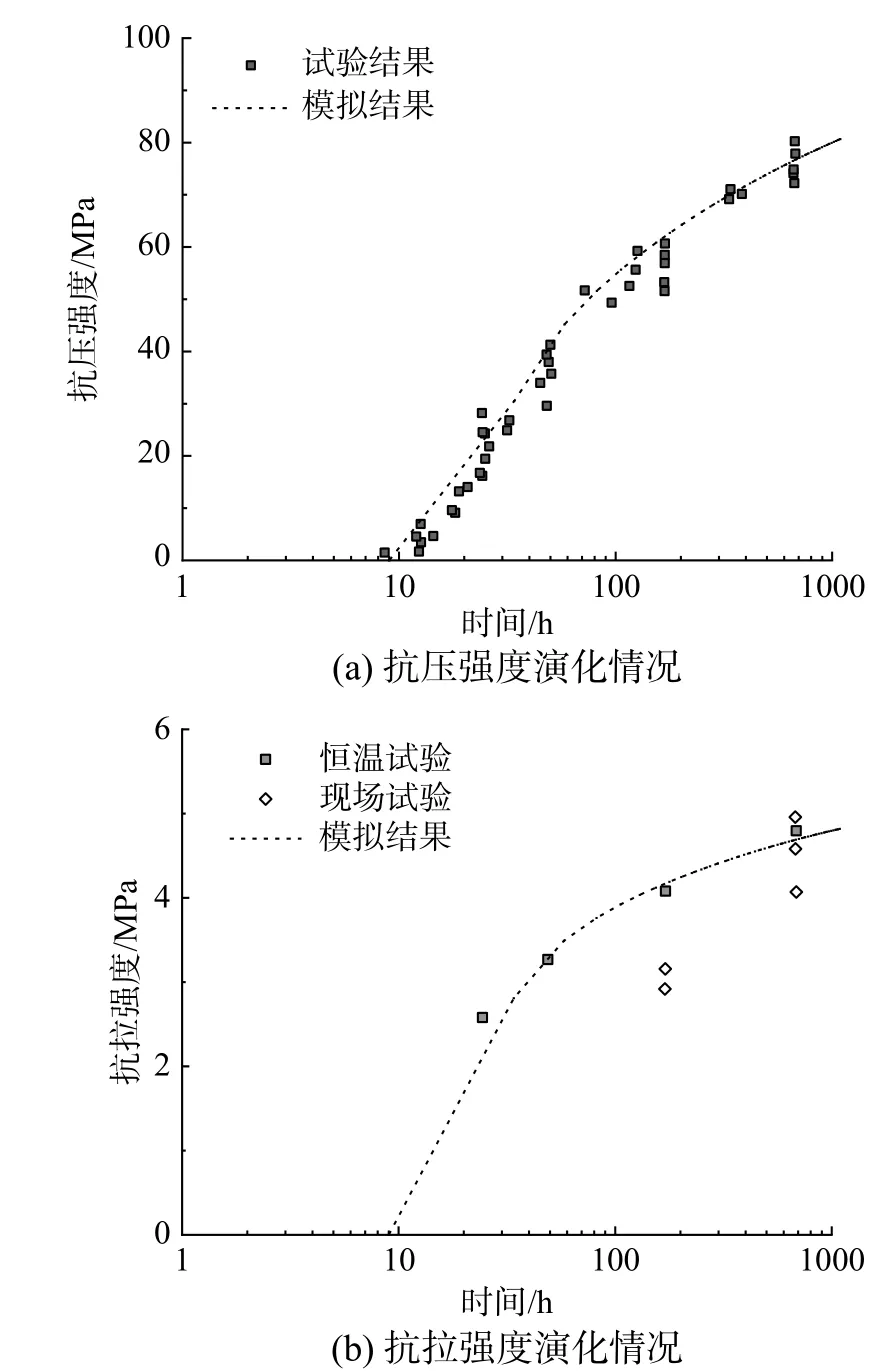
圖6 混凝土強度演化情況Fig.6 Evolution curvesof concrete strength

根據文獻[42]中的徐變試驗，對混凝土的徐變參數進行標定。試驗對三組齡期分別為t0=2 d、3 d、6 d 的混凝土試件軸向施加恒定的壓應力作用，試件尺寸如圖7所示，試件加荷應力與加載時的抗壓強度之比為40%。在試驗過程中，外界環境溫度恒定為20℃，試件處于密封條件以避免發生干燥收縮變形。數值模擬得到的基本徐變柔度演化曲線與試驗結果的對比情況如圖8所示，其中，基本徐變柔度定義為單位應力作用下的瞬時變形與徐變變形之和，徐變參數取值見表2。可以看出，計算結果與試驗結果吻合較好，本文模型可以較好地描述不同加載齡期的混凝土的徐變變形特點。

圖7 圓柱體試件示意圖/mm Fig.7 Schematic diagram of cylinder specimen

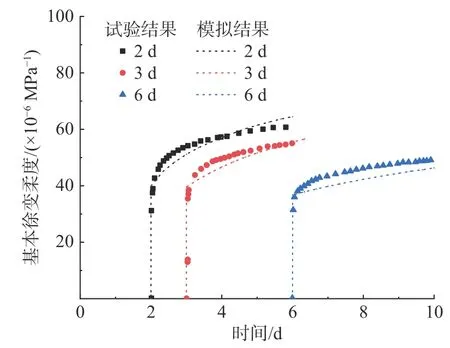
圖8 不同加載齡期的基本徐變柔度演化曲線Fig.8 Evolution curvesof basic creep compliance at different loading ages

表2 徐變試驗模型參數取值Table2 Model parameters in creep tests

至此，本文模型中的化學-熱相關模型參數、強度參數、徐變參數已經全部標定完成。

3.3 計算結果與現場試驗對比

利用3.2小節標定的模型參數，本小節將對“墻體-基礎”結構現場試驗開展數值模擬研究。

為滿足設計尺寸等方面的要求，現場試驗施工過程中在墻體外表面鋪設了模板。如圖9所示，面A 和面B采用的是21 mm 厚的膠合板模板，其中，面A 的模板在混凝土澆筑完成24 h 后拆除，面B在48 h 后拆除。面C采用了10mm 厚的隔熱泡沫模板，在混凝土澆筑完成24 h 后拆除。有限元模擬中根據模板材料的傳熱特性確定結構外表面的對流換熱系數，具體取值見表3。另外，圖10給出了現場試驗實測環境溫度數據[41]，數值模擬中的環境溫度為實測溫度數據的分段線性插值折線。

圖9 “墻體-基礎”結構的熱邊界條件示意圖Fig.9 Schematic diagram of thermal boundary of the wall-foundation structure

表3 模型參數取值Table 3 Model parameters

圖10 實測環境溫度與數值模擬輸入溫度Fig.10 Measured and applied environmental temperature

為了反映墻體溫度的變化情況，試驗在墻體內部布置了溫度傳感器，測點位置見圖2。圖11給出了數值模擬得到的溫度變化曲線與試驗結果的對比情況。可以看出，對于不同的溫度測點位置，模擬結果與試驗實測結果均吻合良好。

圖12和圖13(a)分別給出了試驗墻體裂縫示意圖和數值模擬得到的受拉損傷云圖。可以看出，在現場試驗過程中，混凝土墻體出現了兩條主裂縫，與之對應，在數值模擬過程中，墻體表面也出現了兩個受拉損傷集中區。另外，由于在數值模擬中只考慮了后澆墻體部分的水化過程，基礎部分與后澆墻體部分的剛度差異較大，交界面位置為薄弱區域，因此，圖13(a)中的交界面上也產生了較為嚴重的損傷。總的來說，本文提出的早齡期混凝土多場模型能夠較好地模擬大體積混凝土結構在早齡期階段的開裂過程。

圖12 試驗墻體部分的開裂情況[43]/m Fig.12 The crack pattern in thewallsection

為了探究混凝土徐變變形的影響，進一步在數值模擬過程中不考慮徐變效應，進行對比分析。圖14給出了考慮徐變效應和不考慮徐變效應計算得到的應變、應力演化曲線。結合墻體的溫度變化曲線(圖11)，可以發現，墻體結構在早齡期階段具有以下特點。

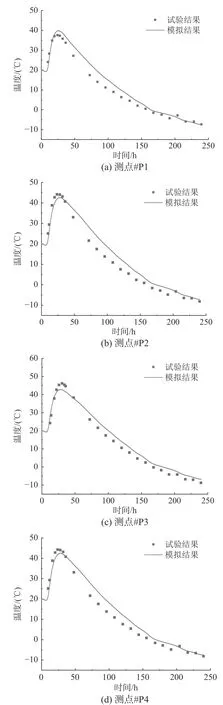
圖11 不同測點的模擬溫度時程曲線與試驗的對比情況Fig.11 Comparisonsof simulated temperature evolution curves w ith experiment at different measured points

在初始階段(0 h～30 h)，混凝土水化反應較為劇烈，墻體溫度迅速升高并產生熱膨脹變形。受周圍約束作用的影響，墻體的熱膨脹變形受到限制從而使得結構內部產生壓應力。在這一階段，混凝土的受壓徐變變形一方面會抵消部分熱膨脹應變，使結構變形減小，另一方面也會產生應力松弛效應，引起墻體內部的壓應力減小，因此，此階段的徐變行為對墻體結構是有利的。

隨后(30 h～100 h)，水化反應速率逐漸減緩，與周圍環境進行熱傳遞引起的熱量損失超過了水化反應釋放的熱量，墻體的溫度開始下降，混凝土的熱膨脹應變不斷減小，并逐漸轉變為收縮變形。與之對應，材料逐漸從受壓狀態轉變為受拉狀態。

在100 h～200 h，水化反應速率進一步減小，墻體溫度繼續下降。在這一階段，混凝土的收縮變形進一步增加，由此產生的拉應力也不斷增加。當內部的拉應力超過材料的抗拉強度時，墻體發生開裂。

由圖14可知，在初始升溫階段，混凝土的徐變行為會引起墻體內部的壓應力減小，并導致拉應力開始出現的時間提前。在隨后冷卻階段，與不考慮徐變效應的工況相比，混凝土的徐變行為會加劇結構的收縮變形，使得墻體的拉應力增加。圖13(b)給出了不考慮混凝土徐變效應計算得到的受拉損傷云圖。與圖13(a)相比，不考慮徐變效應會使得墻體的破壞形態發生轉變。

圖13 墻體的受拉損傷云圖Fig.13 Simulated tensile damage contours

圖14 不同測點的應變、應力隨時間演化曲線Fig.14 Simulated evolution curvesof strain and stressat different measured points

徐變效應對結構的影響并不總是有利的。在早齡期階段，徐變效應的影響會隨著墻體溫度的變化而變化，在升溫階段可以減小壓應力，而在冷卻階段會引起拉應力的增加，并且對結構整體的抗裂性能產生一定的影響。因此，準確評估早齡期階段的混凝土結構，尤其大體積混凝土，的受力性能，需要合理考慮混凝土徐變變形的影響。

4 結論

基于損傷理論框架，本文提出了一類適用于早齡期大體積混凝土力學行為模擬的化學-熱-力多場耦合模型，主要得到如下結論：

(1)將水化反應方程與熱傳導方程耦合處理，建立了化學-熱場耦合作用模型來描述混凝土早齡期階段的水化反應進程與溫度變化。

(2)在化學-熱場耦合作用模型的基礎上，進一步引入彈塑性損傷理論和考慮損傷影響的微觀應力-固化理論，并考慮了熱膨脹變形、自收縮變形和齡期效應，從而建立了適用于早齡期大體積混凝土的化學-熱-力多場耦合模型。

(3)針對早齡期混凝土的多場耦合模型，本文給出了相應的顯式求解算法。該算法將早齡期混凝土的多場耦合問題分解為兩個串行子問題，整個求解過程無需迭代運算，具有較高的運算效率。

(4)基于上述模型和顯式求解算法，首先利用一系列單軸試驗進行模型驗證與參數標定，進而對Maridal 涵洞的“墻體-基礎”結構開展精細化模擬分析。計算結果表明，本文模型可以較好地反映早齡期大體積混凝土的溫度場變化和損傷開裂現象。進一步考察了混凝土徐變變形的影響，對考慮徐變效應和不考慮徐變效應的計算結果進行對比分析。結果表明，伴隨著墻體溫度的變化，混凝土徐變行為從對結構有利逐漸轉變為對結構不利，并且會對結構整體的抗裂性能產生一定的影響。