加權雙Q學習算法優化的PHEV能量管理策略研究

郭玉帆，沈世全，劉冠穎,2，古鴻吉，高 順

(1.昆明理工大學 交通工程學院， 昆明 650500；2.云南開放大學 公共基礎教學部, 昆明 650500)

0 引言

隨著傳統燃油車保有量逐年增長，能源危機與環境污染兩大問題日趨嚴重。為了解決這些問題，車輛轉型勢在必行[1]。由于純電動汽車受限于電能存儲技術，無法滿足長距離出行需求，燃料電池汽車成本昂貴且具有一定的安全隱患，在短期內無法推廣應用，而插電式混合動力汽車(plug-in hybrid electric vehicles,PHEV)作為汽車電動化轉型的過渡產物，相較于傳統燃油車，具有更好的節油效果，并且彌補了純電動汽車續航里程較短的難題，深受各車企的青睞[2]。

能量管理技術是根據混合動力系統各部件的狀態反饋和能量管理策略(energy management strategy,EMS)，實現PHEV不同的動力源的最優能量分配，滿足動力性的同時降低車輛的消耗，是影響PHEV系統性能的關鍵因素之一。因此，設計一個具有良好工況適應性的EMS是改善PHEV燃油經濟性的核心任務[3]。如圖1所示，目前PHEV能量管理策略的研究主要分為三大類：基于規則、基于優化和基于學習[4]。其中基于規則的能量管理策略，主要通過設定相關參數閾值來實現對PHEV的有效控制，由于計算量小、復雜度適中、實時性強等優點，在PHEV中得到了廣泛的應用[5]。基于規則的策略主要依據專家經驗制定，很難保證按照預先定義的規則獲得全局最優策略。為解決上述問題，出現了基于優化的方法，根據優化能力大體可以分為全局優化和實時優化兩大類，極小值原理、動態規劃、模型預測控制和魯棒控制都是極具代表性的優化策略[6]。全局優化策略，雖可得出理論上最優的控制效果，但需要獲取工況全局信息且計算負擔大，難以滿足PHEV的實時控制需求。實時優化策略雖然彌補了這一缺點，但是沒有辦法達到全局最優，同時由于計算量大、適應性較差限制了算法的實際應用[7]。

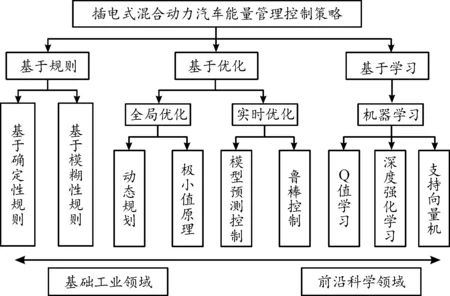
圖1 能量管理控制策略分類框圖

自人工智能應用于最優控制領域以來，強化學習(reinforcement learning,RL)作為一種重要的智能算法，被廣泛用于PHEV能量管理優化問題。Liu等[8]通過對幾種不同駕駛工況數值進行模擬，證明了基于RL的能量管理的適應性、優化性和學習能力。Yang等[9]設計了一種基于雙重深度Q-learning(QL)的EMS，在不同初始值下都取得了良好的燃油經濟性和令人滿意的電池荷電狀態保持性能。Ma等[10]通過使用深度確定性策略梯度算法為混合動力電動履帶車開發了一個在線EMS，其燃油經濟性幾乎達到動態規劃的90%，同時顯著減少了計算時間。Tang等[11]開發了一種新穎的基于雙深度Q網絡學習(double-DQN)的EMS，結合基于規則的發動機啟停策略，控制車輛換擋和發動機節氣門的開度，實現混合動力汽車的多目標優化。Chen等[12]以一款功率分流式PHEV為研究對象，提出了一種基于雙Q學習(double-QL)能量管理策略,與其他策略相比，double-QL策略可以更好地限制電池的最大輸出功率，從而幫助PHEV獲得了更好的經濟性能。

基于QL的能量管理策略兼顧了基于規則和基于優化策略的優點，被廣泛用于混合動力汽車的能量管理問題求解。然而，由于傳統的QL在更新Q函數時使用最大動作值作為最大期望動作值的近似值，造成了動作值的高估，導致QL在隨機環境中變現不佳。受此啟發，雙Q學習算法對傳統QL算法進行了改進，對每一個狀態使用2個Q函數，并將Q函數的動作與其值解耦，避免傳統Q學習的高估問題；但是雙Q學習并不是完全無偏的，依舊存在低估偏差[13]，因此又引入加權函數，使2個Q函數之間存在一個線性關系，減少雙Q學習動作值低估發生的概率。在此基礎上，本文以一款PHEV為研究對象，設計了一種基于加權雙Q學習(weighted double Q-learning,WDQL)的能量管理控制策略，在PHEV的多個動力源之間進行功率分配。最后，在Autonomie平臺上通過Matlab/Simulink搭建整車仿真模型，驗證了所提策略的燃油經濟性和工況適應性。

1 插電式混合動力汽車動力系統建模

本文以豐田Prius功率分流式PHEV為研究對象，其結構如圖2所示，整車主要部件包括2個電機、發動機、電池組、2個逆變器和行星齒輪組構成，其中發動機與行星齒輪組中的行星架機械連接，電機2與太陽輪機械耦合，電池組與逆變器電連接，電機1與齒圈齒輪嚙合，關鍵部件的主要參數見表1所示。

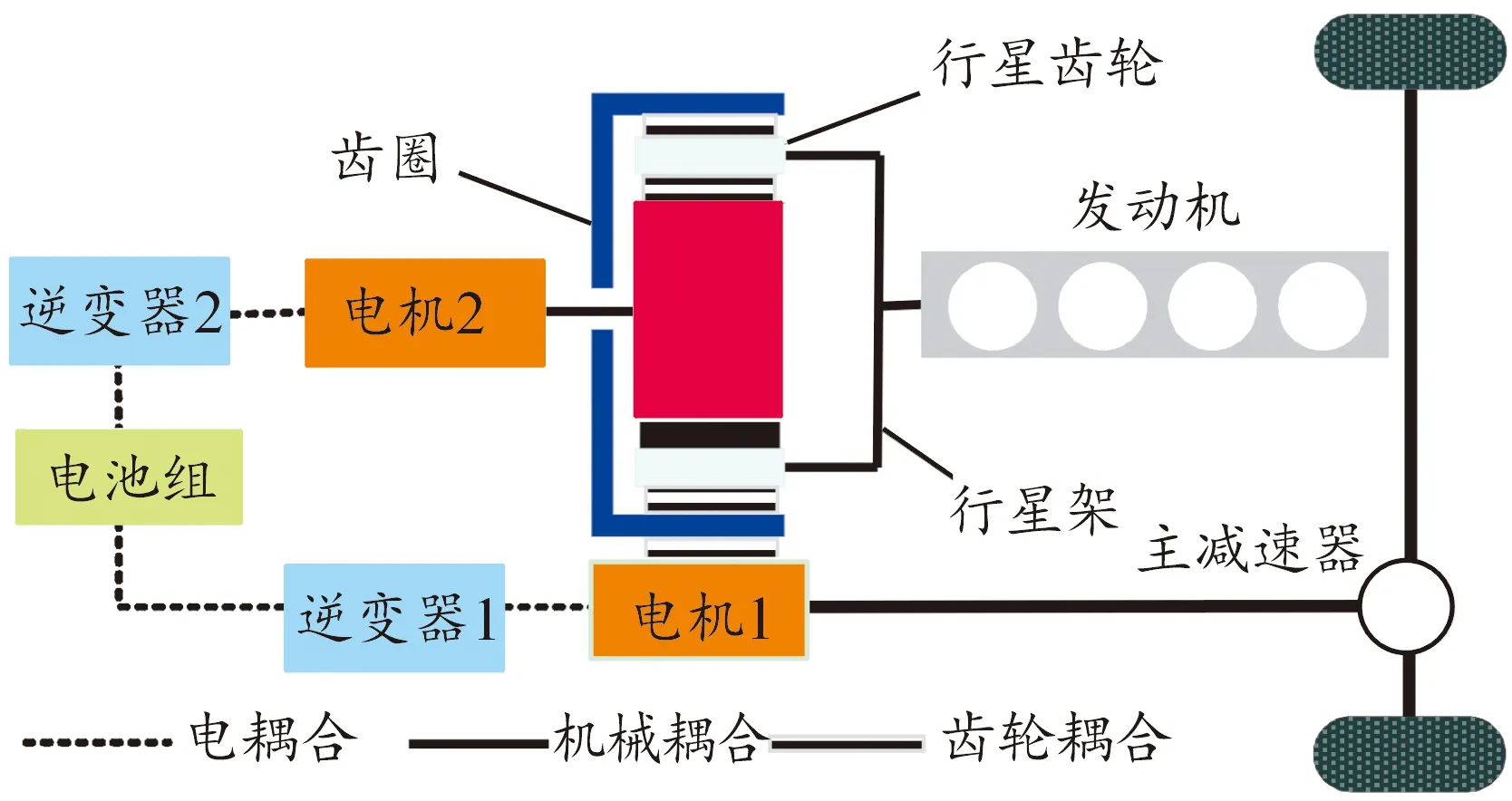
圖2 功率分流PHEV的系統結構示意圖

表1 整車關鍵部件主要參數

1.1 動力總成模型

本文側重于對PHEV的經濟性的研究，對整車的穩定性和舒適性不做過多分析，因此當行駛工況(v)已知時，需求功率Preq可以根據所克服的空氣阻力Fw、坡道阻力Fi、滾動阻力Ff和加速阻力Fj通過整車縱向動力學公式求得：

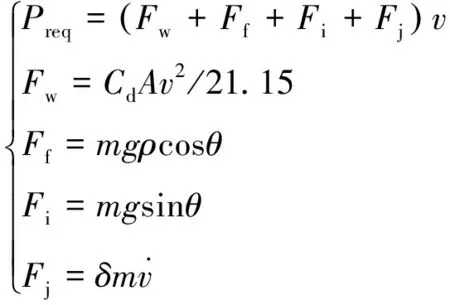
(1)

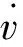
(2)

式中：Preq、Pbat、Peng和Pm分別為主減速器、電池組、發動機和電機的輸出功率；ηf、ηg和ηm分別表示主減速器、齒輪組和電機的傳遞效率；α1∈{-1,1} ，當電機作為電動機為PHEV提供行駛動力時α1=-1，當電機作為發電機給動力電池充電時α1=-1。

1.2 發動機模型

本文重點考慮發動機油耗的計算，在忽略發動機模糊的非線性時變動態特性的情況下，將發動機的瞬時油耗描述為一個映射關系，即發動機油耗模型是關于其轉速與扭矩的相關函數：

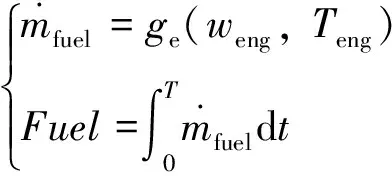
(3)

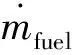
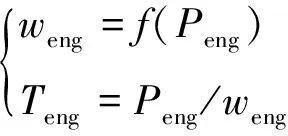
(4)

當發動機轉速和轉矩已知時，每t時刻的燃油消耗率可以通過圖4所示獲得。

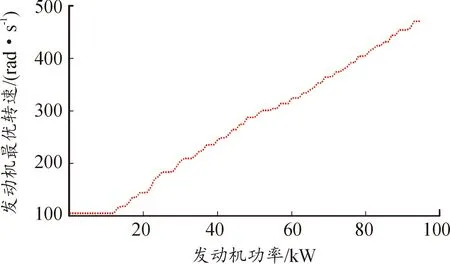
圖3 發動機最優工作曲線

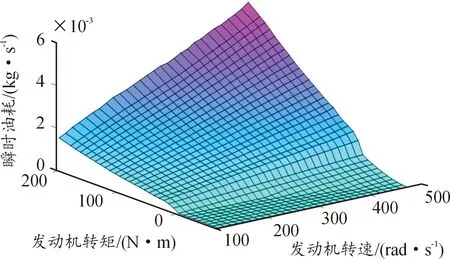
圖4 發動機油耗MAP圖

1.3 電機模型

電機作為PHEV的直接動力部件，具有至關重要的作用。當電機作為電動機使用時，可以作為動力源為車輛提供前進動力；當汽車制動作為發電機使用時，能夠將發動機剩余的能量和制動回收的能量存儲至電池組，從而為電池組補充電能。類似于發動機，電機的轉矩、轉速和效率可以構成電機效率MAP圖，如圖5所示。本文在進行電機建模時，為了減少計算負擔，沒有考慮熱效應等因素對電機性能影響，電機的效率ηm、功率Pm和轉矩Tmot、轉速wmot之間的關系Ψm可以表示為：

(5)

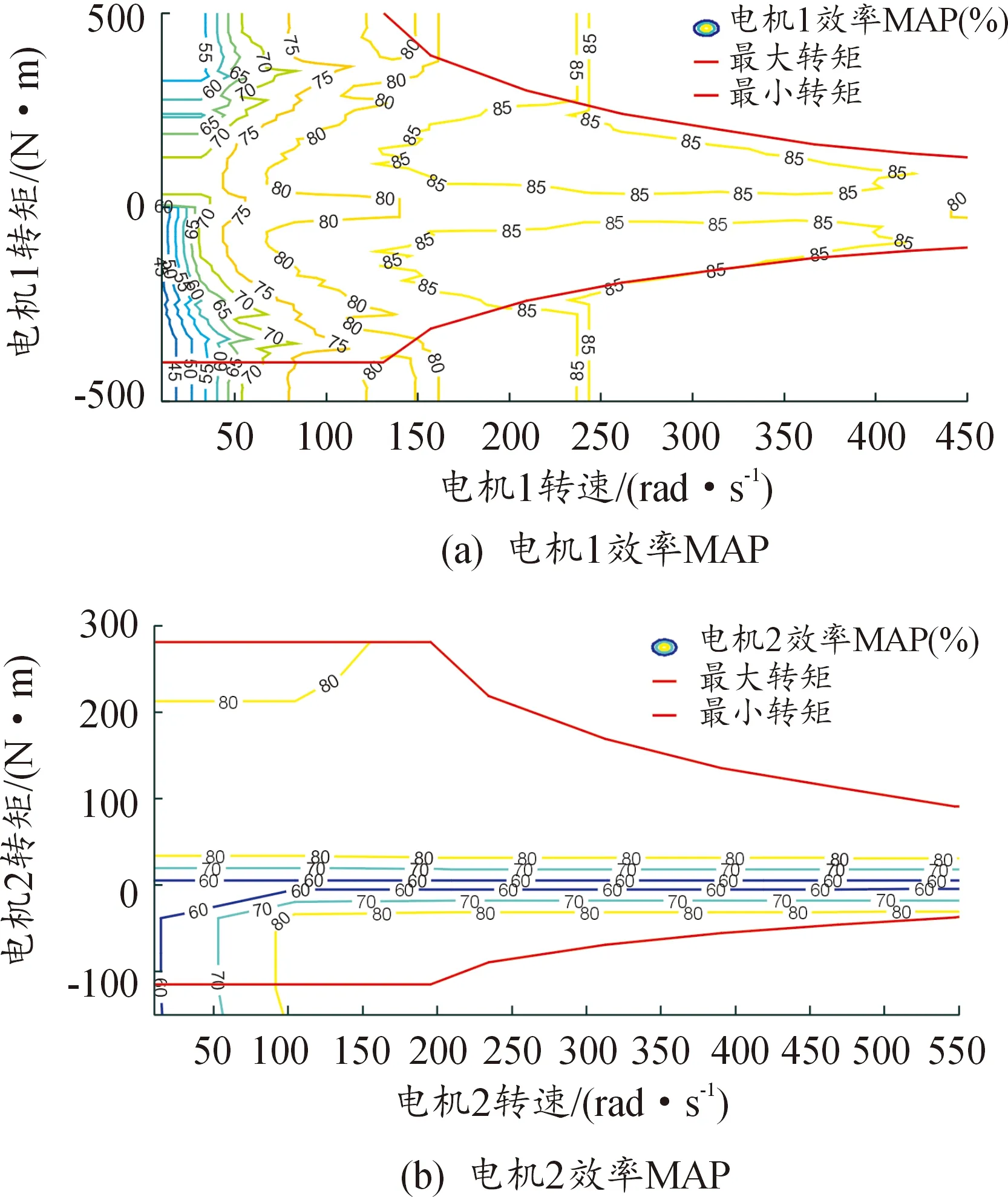
圖5 電機效率MAPs

1.4 鋰離子電池模型

電池組在PHEV中充當著能量存儲系統的角色，既可以回收來自電機轉動產生的能量，又可以輸出能量驅動汽車行駛。本文為了簡化分析，采用一階等效內阻模型來描述電池組工作工程中的充放電特性，其電路如圖6所示。

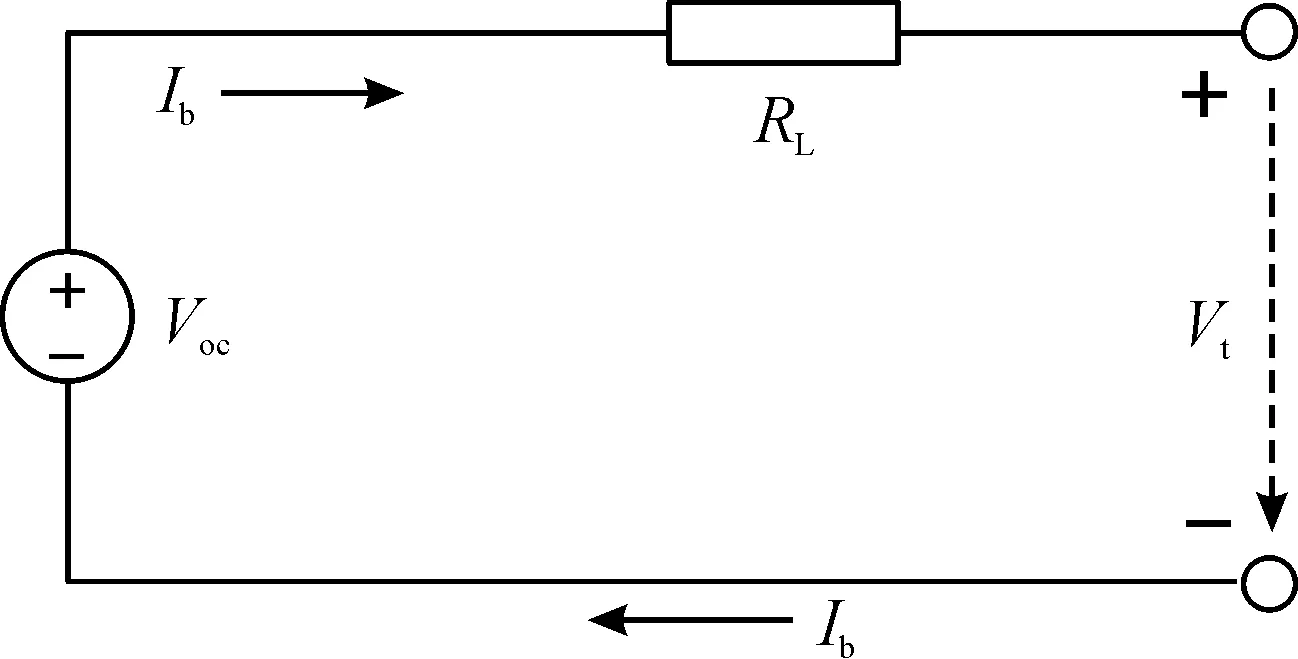
圖6 電池組一階等效電路

根據等效電路模型，若忽略開路電壓動態變化，PHEV的電路關系可描述成電池功率的函數：

Pbat(t)=Voc·Ibat(t)-rintIbat(t)2

(6)

式中：Pbat、Ibat、Voc分別為電池功率、電流和開路電壓；rint為電池內阻。

從而得到電池組的電流函數：

(7)

電池的荷電狀態(state of charge,SOC)作為EMS的主要控制參數，既反映了電池電量使用情況，又影響著電池的內阻，電壓和工作效率，本文通過安時積分法對電池SOC進行估算：

(8)

式中:SOC0表示初始的荷電指數；Qbat指電池總容量(Ah)；若忽略溫度變化和電池老化的影響，Voc和rint隨電池SOC變化，如圖7所示。

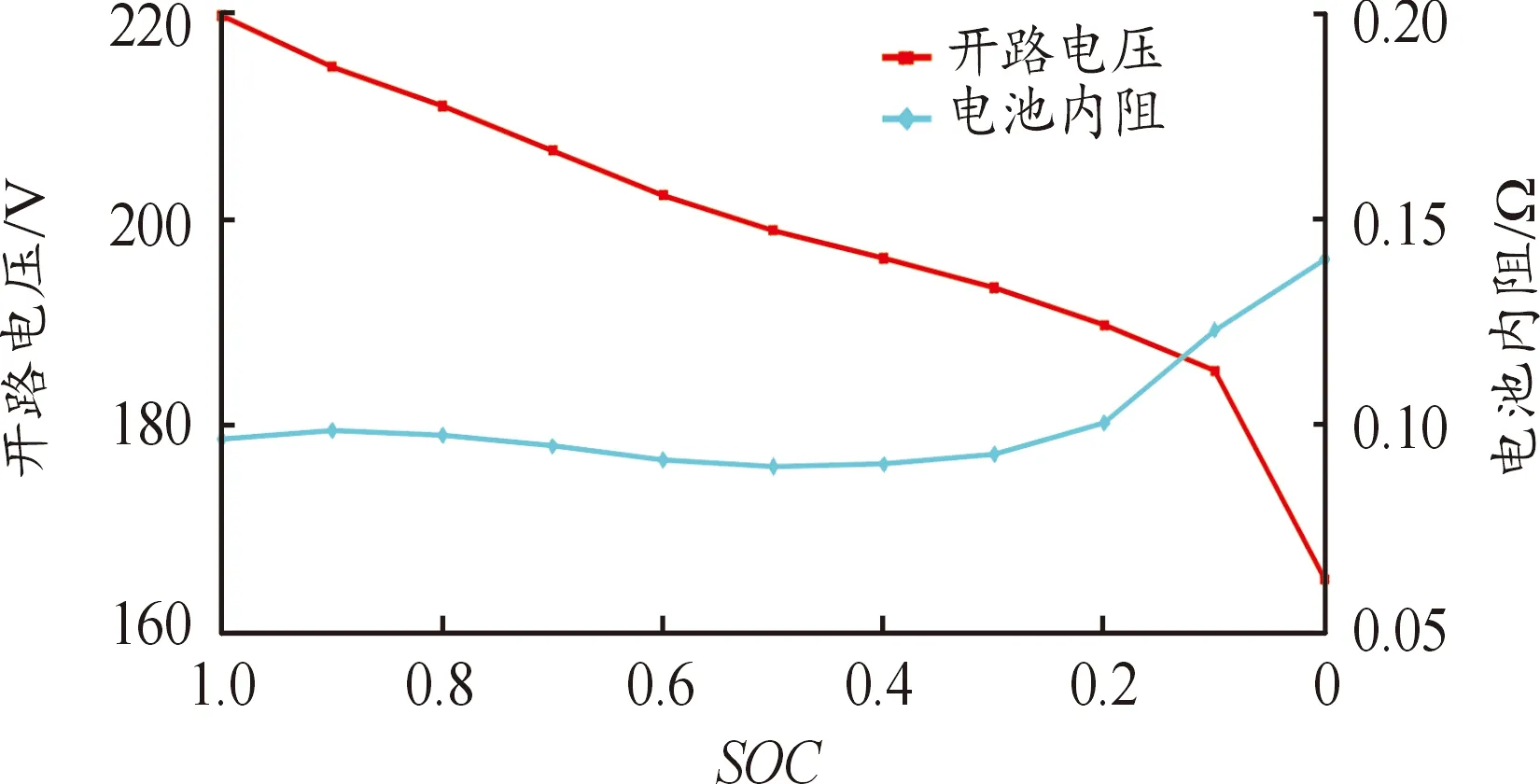
圖7 電池開路電壓和內阻變化曲線

2 加權雙Q學習算法的最優EMS

2.1 插電式混合動力汽車能量管理模型

PHEV的整車能量主要源于電池組提供的電能和發動機提供的燃油，已知行駛工況，在確保動力性的同時合理分配電池組和發動機之間的功率，使PHEV在行駛過程中的燃油消耗和電池電量消耗在一定程度維持均衡是PHEV能量管理控制策略的控制目標[14]。PHEV的能量管理問題作為多目標優化問題，一般將其EMS簡化為非線性的離散系統，其狀態方程f為：

x(t+1)=f(x(t),u(t),t)

t=0,1,2,…,T

(9)

式中：x(t)和u(t)分別為狀態變量和控制變量；T為行駛周期內持續采樣時間。則WDQL策略中的性能優化目標函數J定義為：

ψ(ΔSOC(t)2]dt

(10)

式中：α和ψ是2個權重因子，通過調整2個參數，EMS實現發動機和電池之間的最優功率分配。根據PHEV的功率流關系，當需求功率已知，電池組的功率輸出與發動機輸出功率相關，因此可以把發動機瞬時油耗函數轉化為電池功率相關的函數：

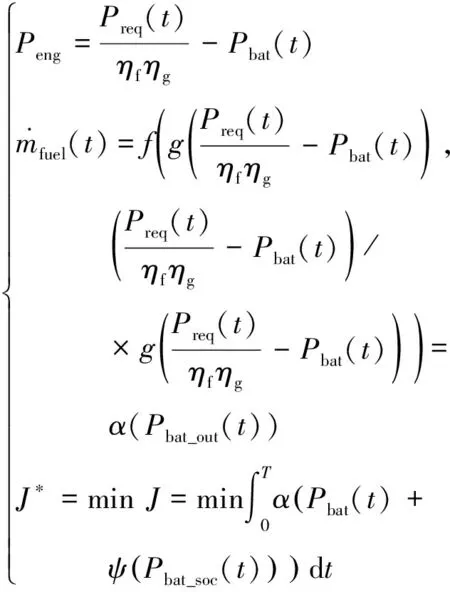
(11)

通過上述分析，在已知行駛工況的需求功率和車速的情況下，可以把電池組的輸出功率作為目標函數的唯一控制量。此外，為了確保PHEV的正常運行，系統狀態必須滿足以下限制條件：

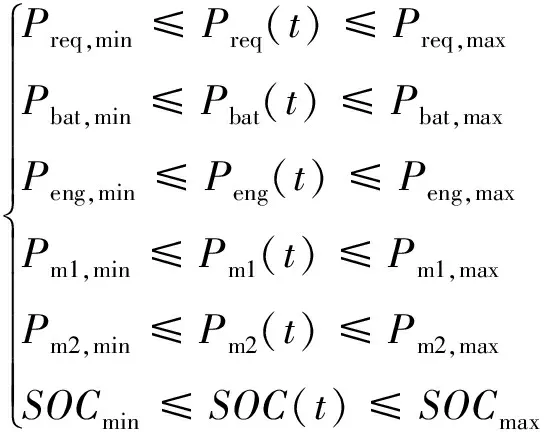
(12)

式中：下標min和max表示各部件參數取值的系統臨界值，并且為了保持較小的電阻，電池的SOC維持在[0.3,0.9]。

2.2 加權雙Q學習算法優化的能量管理控制策略

加權雙Q學習算法是傳統QL的一種改進算法，平衡了常規Q學習算法高估和雙Q學習算法的低估問題[13]。與傳統QL算法相比，WDQL算法使用2個Q函數(QU和QV)來選擇和評估動作，可以避免Q學習中動作值的高估；同時引入加權函數β，使2個Q函數之間存在某種線性關系，降低雙Q學習算法的低估偏差。與傳統的QL算法工作流程相似，如圖8所示，WDQL算法也是智能系統與所在環境連續交互，通過不斷地試錯，收集不同狀態下各種可能動作的獎勵。在學習過程中，首先智能體根據環境傳遞來的即時獎勵值的大小評估所選動作的優劣，然后根據狀態-動作對更新Q函數(QU和QV)，最后通過ε-貪婪算法選擇動作以獲得最大期望獎勵值。

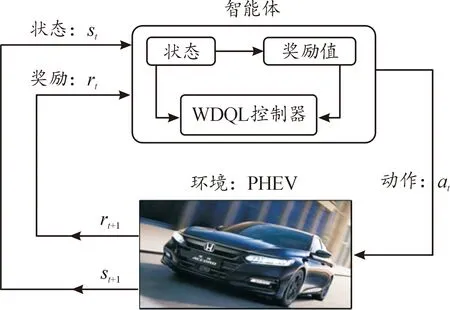
圖8 加權雙Q學習策略控制過程框圖

本文設計一種基于WDQL算法的EMS，實現PHEV中電池和發動機之間最優功率分配，減少PHEV燃油消耗。因此，本文選取需求功率Preq和電池SOC作為狀態變量，電池功率Pbat作為控制變量，將WDQL能量管理策略的變量空間設置為：

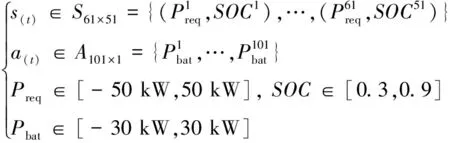
(13)

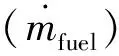
(14)

式中：α和ψ分別表示當前時刻瞬時燃油和電池SOC的權重因子。加權雙Q學習在ε-貪婪算法作用下，WDQL有(1-ε)100%的概率會在QU(s,a)和QV(s,a)中選擇已知并且具有最大動作值的動作，以ε×100%的概率隨機選擇動作。通常ε設置成一個很小的值，在ε-貪婪算法的作用下加強了智能體的動作探索，避免了算法陷入局部最優。

(15)

在WDQL算法中引入決定變量d和隨機變量b，其中，d=0.5、b∈(0,1)，并使用2個變量的比較結果來選擇更新2個Q函數中的其中1個，Q函數更新規則如下：

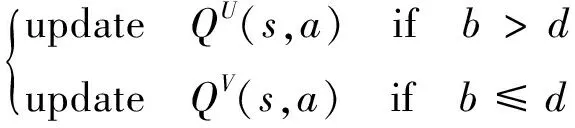
(16)

在確定更新Q函數后，引入加權函數β使得WDQL在更新QU(s,a)和QV(s,a)時使用不同的δ值，加權參數β和最優QU,WDQL函數表示為：

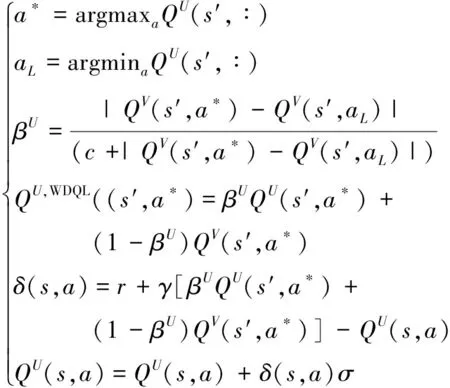
(17)

式中：a*和aL分別表示在下一個狀態s′下，值函數QU能取的最大價值函數值和最小價值函數值對應的動作值；c是常數；σ是學習率；γ是折價因子，用于平衡即時獎勵和延遲獎勵的重要性。從式(17)可以看出，WDQL使用一個QU(s,a)和QV(s,a)的線性組合來求取最優QU,WDQL函數值。因此，QU,WDQL代表了對Q學習的高估和對雙Q學習的低估之間的權衡，這樣可以被認為是對Q函數的無偏估計[13]，類似的更新用于QV(s,a)。加權雙Q學習算法詳細的計算流程如下：

加權雙Q學習算法

1.初始化QU(s,a)，QV(s,a)，s,r,β(s,a)

2.設置學習率σ

3.For episode =1,Mdo

4.Fort=1,2,3，…，Tdo

5.運用ε-貪婪算法根據QU和QV選擇控制動作a

6.執行動作a獲得即時獎勵r和下一狀態s′

7.選擇隨機數b來決定更新QU或者QV

8.ifb>0.5 then

9.a*=argmaxaQU(s′, ∶)

10.aL=arg minaQU(s′,∶)

12.δ(s,a)=r+γ[βUQU(s′,a*)+

(1-βU)QV(s′,a*)]-QU(s,a)

13.QU(s,a)=QU(s,a)+δ(s,a)σ

14.else ifb≤0.5 then

15.a*=argmaxaQV(s′,∶)

16.aL=argminaQV(s′,∶)

18.δ(s,a)=r+γ[βVQV(s′,a*)+

(1-βV)QU(s′,a*)]-QV(s,a)

19.QV(s,a)=QV(s,a)+δ(s,a)σ

20.end

21.s=s′

22.End

23.End

在PHEV的能量管理問題中，若想獲得良好的控制效果，檢測算法有效，需要驗證WDQL算法的收斂性。圖9為WDQL策略在以JC08、US06、LA92、RP05、SC03和WLTC 6個標準工況作為訓練數據下的獎勵函數變化曲線。可以發現，隨著迭代次數的增加，單輪獎勵函數值也迅速增大，直到趨于穩定，這說明基于WDQL的PHEV能量管理控制策略能夠以較快的速度收斂。

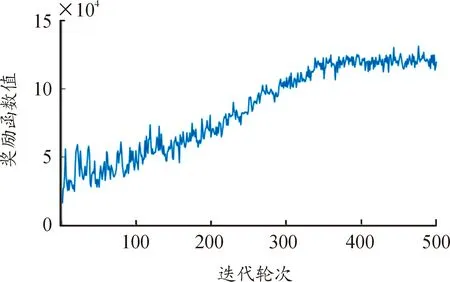
圖9 WDQL算法的獎勵函數曲線

3 仿真與分析

為了評估所提控制策略的效果，將基于隨機動態規劃和基于規則的能量管理策略在工況HWFET、UDDS、NEDC和KM1下的效果與其作對比。測試工況對應的速度曲線如圖10。

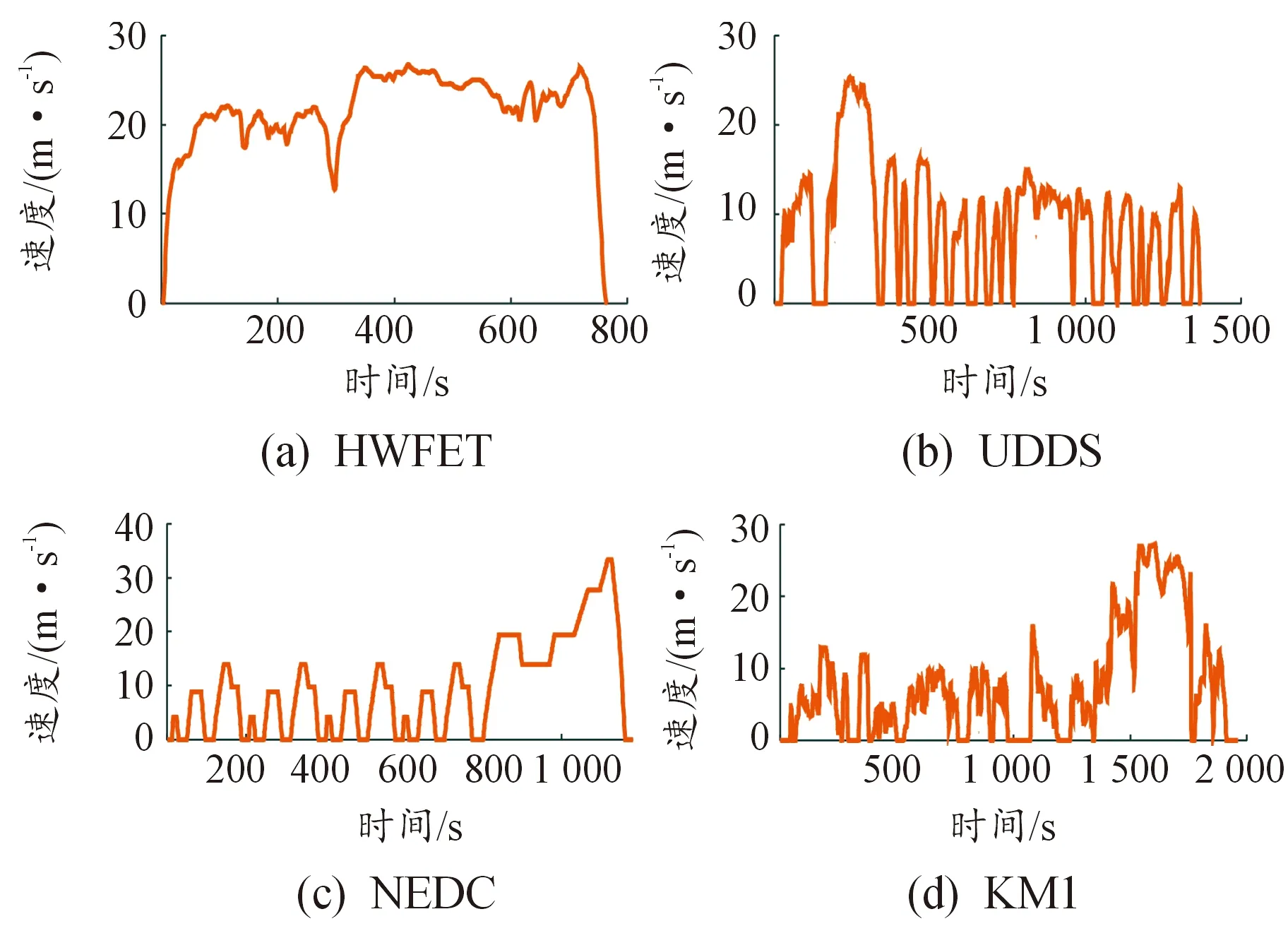
圖10 驗證工況車速曲線

3.1 SDP和CD/CS算法優化的PHEV能量管理策略

隨機動態規劃(stochastic dynamic programming,SDP)是動態規劃和馬爾科夫決策的結合體，既有動態規劃解決全局最優問題的優點，又具備馬爾科夫求解隨機問題的優勢。Lin等[15]針對一款并聯式混合動力汽車，提出了一種基于SDP策略的能量管理策略，仿真結果表明，SDP策略是一種僅次于動態規劃的全局次優的能量管理策略。對于基于SDP算法的PHEV能量管理問題，依舊選取電池功率Pbat作為控制變量，最小累計油耗作為目標函數：

(18)

基于規則的能量管理策略是如今使用最普遍的EMS，本文選取一種放電-維持策略(charge depletion /chare sustaining,CD/CS)作為基準策略。CD/CS策略是一種典型確定性規則策略,不需要提前預知未來工況，可以充分利用電池電能實現在線計算[16]。CD/CS策略由CD模式和CS模式2種模式組成，在CD階段，電池電量充足，電池是主要供能裝置，只有當電池最大功率無法滿足汽車行駛所需功率時，發動機才會短暫啟動；當電池SOC下降到預設閾值則進入CS階段，發動機作為主要供能裝置，并對電池進行補充充電，使電池SOC維持在閾值附近。CD/CS策略用數學公式描述為：

(19)

3.2 能量管理策略效果的對比分析

建立好各種控制策略以后，通過Autonomie對測試工況進行仿真分析。圖11為3種控制策略在不同工況下的油耗表現，可以看出，相比較于CD/CS策略，WDQL策略在各個工況下的油耗都呈現出不同程度的下降趨勢，且與SDP策略下的油耗相差不大。

圖12為不同策略在不同復合行駛工況下的SOC的變化曲線，可以看出，相比CD/CS策略，基于WDQL策略的工作狀態不再單純由電池SOC決定，而是控制策略根據最優目標函數來控制PHEV的發動機工作狀態，頻繁調用發動機介入工作，輔助動力電池來共同驅動車輛，延遲了電池SOC下降到預設閾值的時間，使電池電量下降速率明顯降低，更好地控制電池的功率輸出，表明WDQL策略能夠將電池的SOC維持在一定范圍，從而降低汽車燃油消耗并減少尾氣排放。

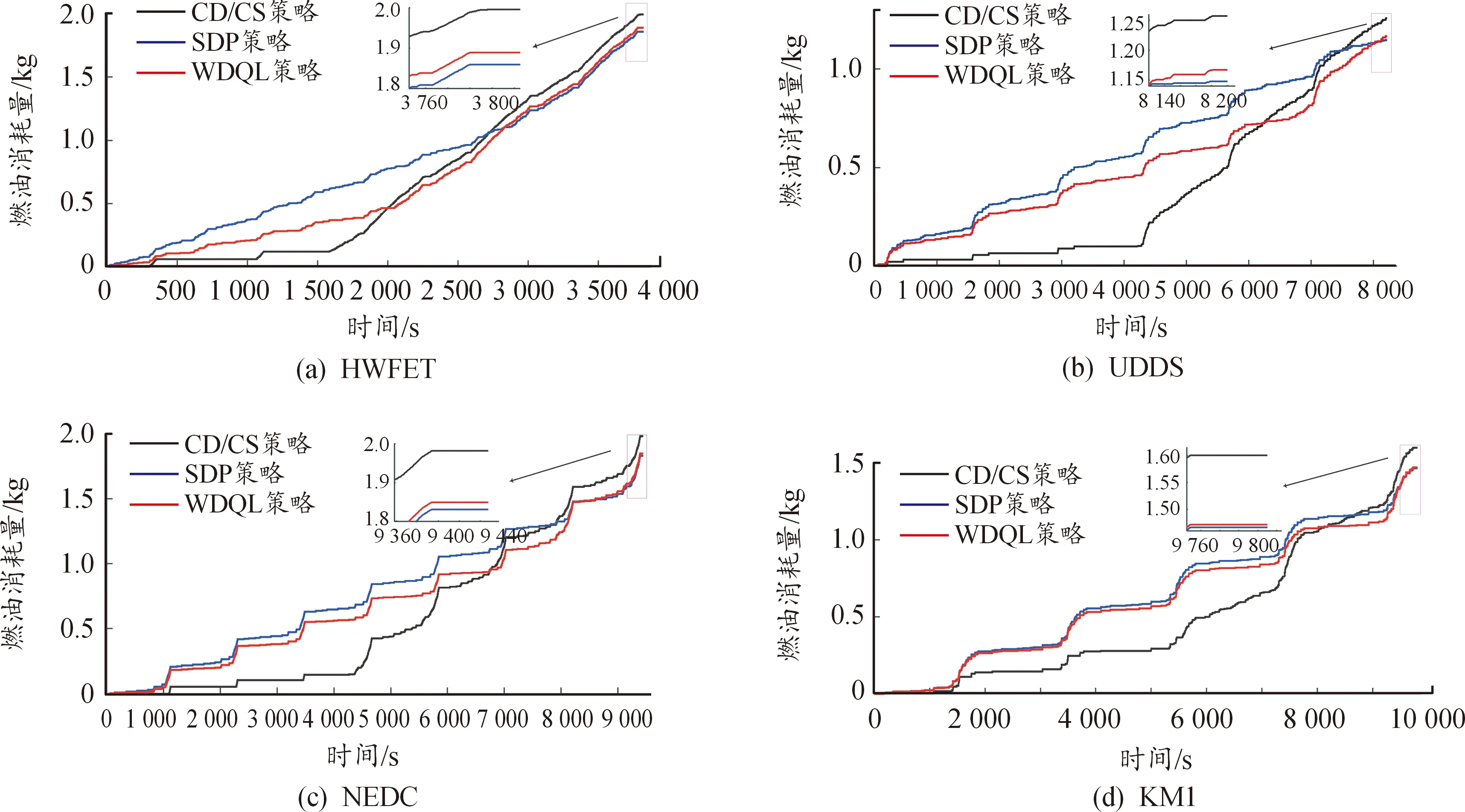
圖11 復合工況的油耗曲線

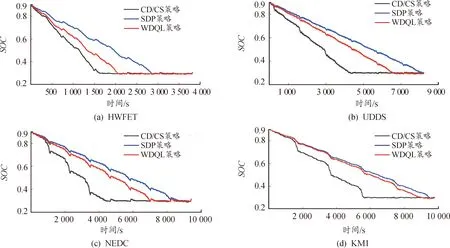
圖12 SOC變化曲線

基于WDQL策略中的獎勵函數僅僅影響瞬時控制動作的選擇，使得在該策略下最終電池SOC具有相應的偏差，為了使所提策略下的燃油經濟性更有說服力，存在的SOC偏差將以能量守恒原則等效為燃油消耗量[6]。表3為CD/CS策略和WDQL策略在不同組合工況下的能耗。對比CD/CS策略，數據直觀地顯示出WDQL策略燃油經濟性分別提高了5.66%、6.70%、6.99%和5.51%，證明了所提策略的有效性。SDP策略作為全局優化策略，可以實現PHEV整車的最優燃油經濟性，由表4可以看出，基于WDQL的能量管理策略可以實現SDP策略的98%以上的燃油經濟性，證明了所提策略的次優性和對不同的駕駛循環工況具有良好的燃油經濟性。

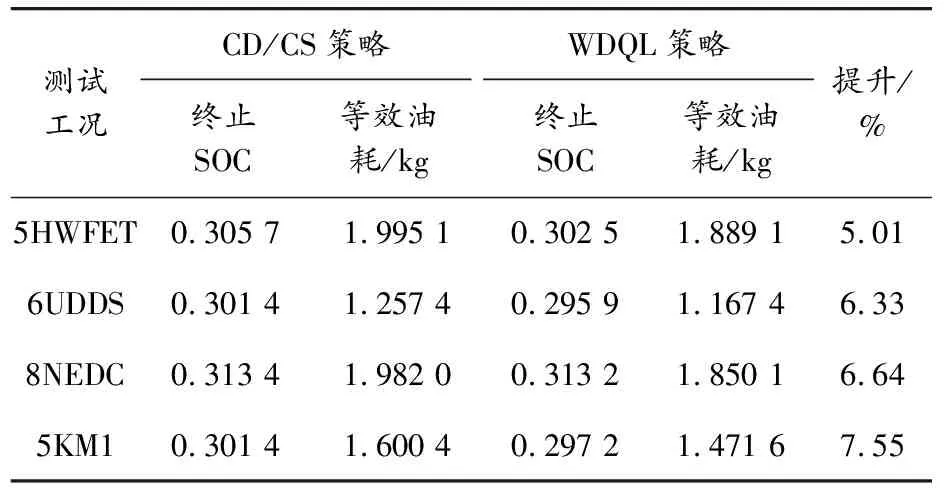
表3 CD/CS策略與WDQL策略燃油經濟性

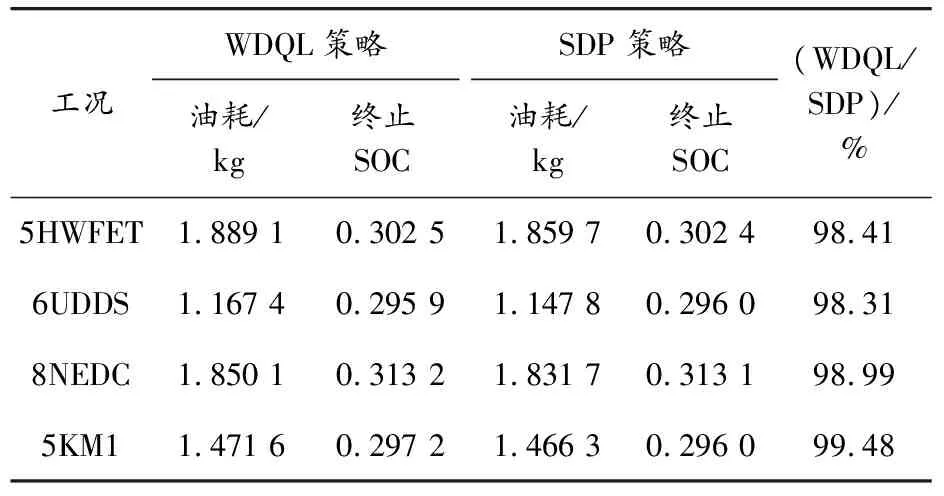
表4 SDP策略與WDQL策略燃油經濟性

不同工況下各控制策略的發動機工作點如圖13所示。可以發現SDP策略下，發動機的工作點幾乎完全在最優工作曲線上，CD/CS策略由于發動機的頻繁啟動，工作點主要集中在低功率和較低功率的區間，而本文所提策略相比CD/CS策略，發動機的工作點軌跡明顯沿著最優曲線上移，和SDP策略下發動機工作點軌跡接近，且由于WDQL策略的學習能力，發動機的啟停頻率明顯小于其他策略。這說明，所提策略能夠合理地分配發動機和電池的功率，緩解發動機工作在低轉矩、低效率工作區間的概率，從而提高了PHEV的燃油經濟性。

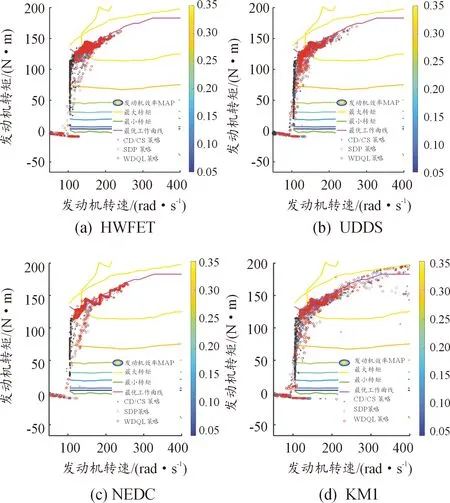
圖13 發動機工作點在效率MAP上的對比

4 結論

本文以PHEV為研究對象，提出了一種基于加權雙Q學習算法能量管理策略，該策略不僅可以平衡常規Q學習算法高估和雙Q學習算法的低估問題，還能提高PHEV燃油經濟性。通過仿真分析，得出以下結論：

1) 基于加權雙Q學習的PHEV能量管理策略可以平衡常規Q學習算法高估和雙Q學習算法的低估問題，減少了隨機性的影響，在不同的工況下具良好的適應性并可以實現較好的燃油經濟性。

2) 基于加權雙Q學習的PHEV能量管理策略能夠使發動機避免在低效率區域工作，而更多工作在發動機高效率區，從而有效提升發動機工作效率，降低了PHEV在運行過程中的燃油消耗。

3) 基于加權雙Q學習的PHEV能量管理策略可以延遲電池SOC下降到預定閾值的速度，更好地控制電池功率輸出，提高PHEV的燃油經濟性。