行走機械腿部軌跡規劃及運動特性分析

王智森，范云波

(景德鎮學院 機械電子工程學院，江西 景德鎮 333400)

通過模仿自然界生物形態結構及運動特征進行仿生機械裝置創新設計的方法有著非常悠久的歷史[1]。早在15世紀，基于模仿鳥類飛行的靈感，著名畫家達芬奇繪制了撲翼機圖；到19世紀，科學家利用空氣動力學原理設計成功了單翼和雙翼滑翔機；21世紀以后，隨著人工智能領域技術不斷革新，各類仿生機械技術呈井噴式發展，成為一個熱門的研究方向[2-4]。張德義等模仿魚類外形及運動模式設計了一種仿生三關節機械魚，通過理論及實驗研究魚體與舵機擺動之間的運動規律[5]；雷方濤等模擬鷹類飛行特點設計并制造了一種仿生機械鷹，配合輔助設備用于機場進行驅鳥，起到了一定的效果[6]；黃世明等模仿魚類的游動原理，借助Adams仿真軟件設計了一種仿生機械魚魚尾擺動機構，實現泳動方式運動提供動力[7]。本文通過觀察螃蟹的行走姿態，模仿設計了一種行走機械腿部結構，研究腿部行走軌跡規劃及運動特性。

1 行走機械腿部結構設計

1.1 腿部運動軌跡規劃

研究行走機械腿部行走軌跡及運動特性，重點針對腿部系統單獨一條腿的足端進行軌跡規劃。其中單腿系統是在模仿螃蟹行走姿態的運動特點基礎上進行設計，足端的軌跡與螃蟹行走的軌跡類似。將行走機械跨步過程簡化為4個階段：上升、前跨、下降、觸地，軌跡形狀如圖1所示，近似為一條拋物線與一條水平直線連接而成。其中拋物線部分是腿部足端抬起向前跨步的過程，水平直線部分是腿部足端著地不動，作為整個行走機械的支撐，而其他腿在完成跨步運動。

圖1 腿部跨步軌跡

1.2 腿部自由度計算及機構求解

行走機械的腿部設計是由多個關節連接在一起的構件組合而成，其中各桿件組成平面搖桿機構和平面雙搖桿機構，重點在設計平面搖桿機構時必須確定桿長與曲柄存在的成立條件。本文設計的行走機械腿部機構運動簡圖如圖2所示，其中桿件d為機架，桿件a為曲柄，主要分為5個部分：由桿件a、b、c、d組成的平面搖桿機構1；由桿件a、d、g、h組成的平面搖桿機構2；由桿件f、g、j、i組成的平面雙搖桿機構；由桿件c、f、e組成的三角形固定構件1；由桿件l、k、j組成的三角形固定構件2。

腿部動力通過曲軸帶動曲柄和各機構來傳遞，運動自由度為1。平面連桿機構的自由度計算如式(1)所示。

F=3n=(2PL+PH)

(1)

圖2中活動構件數目n為7，低副數目PL為10，高副數目PH為0，代入式(1)中計算求解得到腿部機構自由度為1，符合設計要求。

圖2 腿部機構運動簡圖

利用解析法計算求解平面搖桿機構1的尺寸參數，建立XOY坐標系如圖3所示，其中α0、Ψ0分別為曲柄、搖桿初始位置時與x軸的夾角，θ1i、θ2i、θ3i分別為曲柄、連桿、搖桿從初始位置開始轉動的角度，列出矢量方程如式(2)所示。

圖3 平面搖桿機構求解

+=+

(2)

向x、y軸分別投影可得如式(3)所示。

(3)

將式(3)消去θ2i整理后可得如式(4)所示。

b2=a2+c2+d2+2dccos(θ3i+Ψ0)-

2adcos(θ1i+α0)-2accos(θ3i+Ψ0-θ1i-α0)

(4)

cos(θ1i+α0)=mcos(θ3i+Ψ0)-

(5)

cos(θ1i+α0)=p0cos(θ3i+Ψ0)+

p1cos(θ3i+Ψ0-θ1i-α0)+p2

(6)

平面雙搖桿機構的設計求解過程與上述類似，作用是將2個曲柄搖桿機構生成的路徑進行傳遞。給定初始位置參數值α0=Ψ0=0°，定義3組平面雙搖桿機構運動角度特征值，如表1所示。

表1 平面雙搖桿機構運動角度 (°)

將平面雙搖桿機構初始位置參數值及3組運動角度特征值分別代入式(6)計算可得：p0=1、p1+p2=0，即平面雙搖桿機構尺寸參數g=i=30mm。基于設計的三角形固定構件形狀為等腰直角三角形，得到平面雙搖桿機構其余兩桿尺寸參數f=j=30mm，即形狀構成菱形。

1.3 腿部結構設計

行走機械的曲軸是連接電機部件與腿部各機構的傳動零件，要求具有良好的抗沖擊載荷性能且耐磨損。通過觀察螃蟹腿部行走姿態，針對螃蟹腿部結構進行簡化處理，模仿設計6條腿對稱分布完成行走動作。為了保證各腿部結構關節之間的協同平衡性，將曲軸上的3個曲柄設計成空間120°均布布置。行走機械的支撐骨架設計成三角形結構，滿足穩定性設計要求。根據1.2節單腿各機構求解得到的尺寸參數，借助UG軟件完成行走機械腿部部件、曲軸、支撐骨架等結構的三維建模并進行裝配，得到行走機械腿部整體結構如圖4所示。

圖4 行走機械腿部結構

2 行走機械腿部運動特性研究

2.1 腿部關節運動軌跡

借助UG軟件的運動仿真分析功能，基于UG的后置處理器Post Builder模塊，對行走機械腿部關節運動特性進行研究[8-10]。仿真模擬過程主要分為2個部分：建立運動仿真模型；進行運動仿真實驗，分析流程如圖5所示。

圖5 腿部關節運動仿真分析流程

針對行走機械單腿進行運動仿真，各機構裝配順序尤為重要，避免關節出現過約束現象。在運動仿真過程中，根據整體機構的自由度及運動副關系確定各構件約束形式，其中2個三角形固定構件需要定義為無運動副固定連桿，逐次對各機構連桿添加運動副，如旋轉副、柱面副等，最后添加解算方案，定義解算類型、分析類型、時間、步數及重力方向等并進行求解。給行走機械單腿各關節編號，通過使用追蹤命令來觀測各關節的運動軌跡如圖6所示。

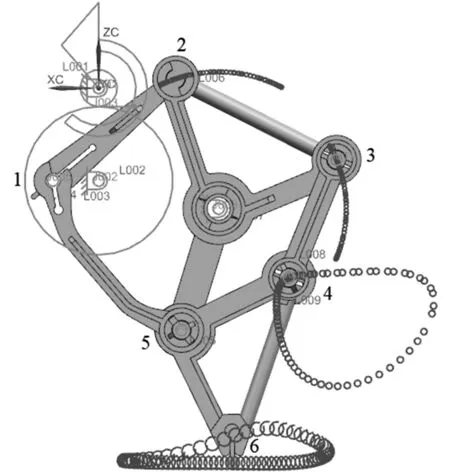
圖6 腿部關節運動軌跡

由運動仿真分析結果可知：在曲軸曲柄的驅動下關節1做圓周運動，關節2、3、5做搖擺往復運動，關節4、6的運動軌跡分別為一條封閉的曲線構成1個循環。分析關節6即足端的運動軌跡曲線，可以細分為4個階段：上升、前跨、下降、觸地，其中上升、下降階段與地面的夾角與跨越障礙物能力有關，夾角在確保行走機械腿部支撐骨架不發生傾覆的正常范圍內越大，表明跨越障礙物的能力越強。

2.2 腿部關節速度分析

設定行走機械的曲軸曲柄初始角速度為40rad/s，通過單腿運動仿真分析過程，測量得到各關節點的速度曲線，分別選取搖桿關節點2的速度曲線如圖7所示，及足端關節點6的速度曲線如圖8所示，進行分析。

圖7 搖桿關節點2速度曲線

圖8 足端關節點6速度曲線

由搖桿關節點2和足端關節點6的速度曲線圖可知：速度變化平穩，沒有出現突變現象，不會造成剛性沖擊，符合行走機械腿部的運動連續性要求，速度呈柔性增加，各關節之間沒有發生干涉，行走過程平穩。1個運動循環中回程速度變化較快，符合機構的急回運動特性，節省空回行程的時間，提高行走效率。

2.3 腿部關節加速度分析

加速度在機械運動過程中是一個十分重要的參數，變化規律影響機械運動過程的穩定性。同理腿部關節速度分析流程，分別選取搖桿關節點2、足端關節點6關鍵節點進行分析，通過運動仿真結果分別測得上述2個關節點的加速度曲線如圖9和圖10所示。

圖9 搖桿關節點2加速度曲線

圖10 足端關節點6加速度曲線

由搖桿關節點2和足端關節點6的加速度曲線圖可知：在1個行走循環周期內，加速度變化平穩，回程加速度較大，說明回程階段速度變化很快，驗證了腿部機構運動的急回特性，有利于提高腿部行走效率及越過障礙物能力。加速度變化曲線連續不間斷，不會造成柔性沖擊，各關節之間運動沒有出現干涉現象，提高了機構可靠性，驗證了腿部機構運動的可行性及穩定性。

結語

(1)本文通過觀察螃蟹行走姿態，研究腿部各關節之間的運動協同性特點，完成了行走機械腿部的運動軌跡規劃、自由度計算及機構求解、結構設計、運動軌跡仿真及運動特性研究的一體化分析流程。

(2)借助UG軟件完成行走機械腿部部件、曲軸、支撐骨架等結構的三維建模并進行整體結構裝配。通過運動仿真分析功能模塊的追蹤命令觀測腿部各關節的運動軌跡，驗證足端運動軌跡分為4個階段：上升、前跨、下降、觸地。上升、下降階段與地面的夾角在一定范圍內越大，表明腿部跨越障礙物的能力越強。

(3)由腿部關鍵節點速度及加速度曲線分析結果可知：在1個行走循環周期內，行走機械腿部速度及加速度變化平穩，沒有發生突變，各關節之間無干涉現象，表明腿部機構運動的可行性及穩定性，為后續腿部結構優化設計提供理論依據。