基于GI-AMED的滾動(dòng)軸承早期故障診斷

崔奔，郭盼盼，張文斌

(1.昆明理工大學(xué) 機(jī)電工程學(xué)院，昆明 650500；2.紅河學(xué)院 云南省高校高原機(jī)械性能分析與優(yōu)化省重點(diǎn)實(shí)驗(yàn)室，云南 蒙自 661199)

滾動(dòng)軸承是機(jī)械設(shè)備中應(yīng)用廣泛的部件，也是極易損壞的部件，其運(yùn)行狀況直接影響整個(gè)旋轉(zhuǎn)機(jī)械設(shè)備的穩(wěn)定性，對(duì)滾動(dòng)軸承進(jìn)行健康狀態(tài)評(píng)估和早期故障診斷具有十分重要的意義[1]。滾動(dòng)軸承發(fā)生故障時(shí)會(huì)產(chǎn)生一系列的周期性脈沖，從被噪聲污染的振動(dòng)信號(hào)中提取脈沖特征是軸承故障診斷的關(guān)鍵步驟[2-3]。

最小熵解卷積(Minimum Entropy Deconvolution，MED)于2007年首次應(yīng)用于軸承與齒輪的故障診斷[4-5]，國(guó)內(nèi)學(xué)者陸續(xù)將其與稀疏分解[6]、變分模態(tài)分解[7]、支持向量機(jī)[8]、聯(lián)合平方包絡(luò)譜[9]等方法相結(jié)合，用于滾動(dòng)軸承微弱故障特征的提取和分類(lèi)。最小熵解卷積通過(guò)最大化軸承振動(dòng)信號(hào)中沖擊分量的峭度值并最小化其他噪聲分量的峭度值[3]實(shí)現(xiàn)故障信號(hào)的降噪并突出沖擊成分，其降噪效果取決于濾波器長(zhǎng)度的選取。模糊熵是一種可以表征信號(hào)復(fù)雜程度的熵[10]，軸承振動(dòng)信號(hào)經(jīng)最小熵解卷積降噪后，周期性脈沖成分與噪聲成分分離，信號(hào)由無(wú)序變有序，模糊熵值也由大變小，可將模糊熵作為標(biāo)準(zhǔn)實(shí)現(xiàn)最小熵解卷積參數(shù)的自適應(yīng)選取。

基尼系數(shù)[11]是經(jīng)濟(jì)學(xué)中用來(lái)衡量收入分配均勻程度的指標(biāo)，滾動(dòng)軸承振動(dòng)狀態(tài)出現(xiàn)異常時(shí)，監(jiān)測(cè)信號(hào)呈現(xiàn)的稀疏性與經(jīng)濟(jì)學(xué)中描述居民收入分配的不均衡性相似。因此，本文將基尼系數(shù)用于處理軸承退化數(shù)據(jù)，判斷軸承產(chǎn)生早期故障的時(shí)間范圍；并采用自適應(yīng)最小熵解卷積進(jìn)行降噪預(yù)處理，通過(guò)包絡(luò)解調(diào)實(shí)現(xiàn)軸承故障特征的提取。

1 理論分析

1.1 最小熵解卷積

最小熵解卷積的實(shí)質(zhì)是通過(guò)解卷積的計(jì)算過(guò)程尋找最優(yōu)逆?zhèn)鬟f函數(shù)，并作用于輸入信號(hào)，以此恢復(fù)信號(hào)中的沖擊脈沖[12]。滾動(dòng)軸承的振動(dòng)信號(hào)y(n)可以表示為

y(n)=h(n)*x(n)+e(n)，

(1)

則

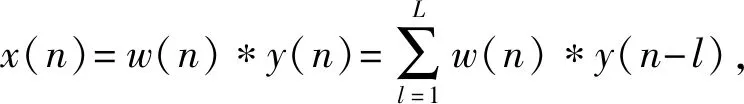
(2)

式中：x(n)為沖擊信號(hào)；h(n)為傳遞函數(shù)；e(n)為噪聲成分；w(n)為最優(yōu)逆?zhèn)鬟f函數(shù)；L為逆濾波器的長(zhǎng)度。

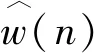
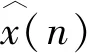
(3)

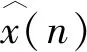
(4)

則

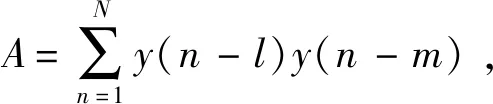
(5)

(6)

式中：b為y(n)和x(n)的互相關(guān)矩陣；A為y(n)的自相關(guān)矩陣。

最小熵解卷積的算法可以歸納如下[12]：

1)初始化w(0)中的元素全為0；

2)迭代計(jì)算x(n)=w(n)i-1*y(n)；

3)計(jì)算b(i)(l)；

4)計(jì)算w(i)=A-1b(i)；

1.2 模糊熵

模糊熵用于描述時(shí)間序列的復(fù)雜度，廣泛應(yīng)用于機(jī)械設(shè)備的故障診斷領(lǐng)域[13]。對(duì)于時(shí)間序列X={X1,X2,…,XN}，構(gòu)造m維向量X(i)=[Xi,Xi+1,…,Xi+m-1]，其中1≤i≤N-m。則X(i)，X(j)對(duì)應(yīng)元素之差中絕對(duì)值的最大值為

(7)

借助模糊隸屬度函數(shù)測(cè)量向量X(i)，X(j)之間的相似程度。模糊隸屬度函數(shù)為

(8)

則互相關(guān)概率的平均值為

(9)

對(duì)于維數(shù)m+1，迭代(7)—(9)式可得到Bm+1(r)，則模糊熵可表示為

EFE(m,r,N)=lnBm(r)-lnBm+1(r)，

(10)

本文選取模糊熵的維數(shù)m=2，相似容限r(nóng)=0.2[14]。

1.3 基尼系數(shù)

當(dāng)滾動(dòng)軸承出現(xiàn)故障時(shí)，其振動(dòng)信號(hào)的能量通常集中在信號(hào)序列的某些位置，故障信號(hào)呈現(xiàn)出的稀疏性與經(jīng)濟(jì)學(xué)中描述居民收入分配的不均衡性很類(lèi)似，因此可利用基尼系數(shù)表征滾動(dòng)軸承故障的發(fā)展趨勢(shì)并進(jìn)行健康狀態(tài)評(píng)估。對(duì)于時(shí)間序列X={X1,X2,…,XN}，向量Xi為

(11)

則基尼系數(shù)可表示為

(12)

式中：A為時(shí)間序列的正序排列；F為時(shí)間序列的和；基尼系數(shù)G的取值范圍為[0，1]。

1.4 診斷步驟

最小熵解卷積的參數(shù)優(yōu)化流程如圖1所示，濾波器長(zhǎng)度L的取值范圍為2～300，將原始振動(dòng)信號(hào)輸入最小熵解卷積中進(jìn)行優(yōu)化，得到最佳L并獲得自適應(yīng)最小熵解卷積。將原始振動(dòng)信號(hào)輸入自適應(yīng)最小熵解卷積中進(jìn)行降噪處理，然后經(jīng)過(guò)包絡(luò)解調(diào)提取出故障特征頻率，具體診斷流程如圖2所示。

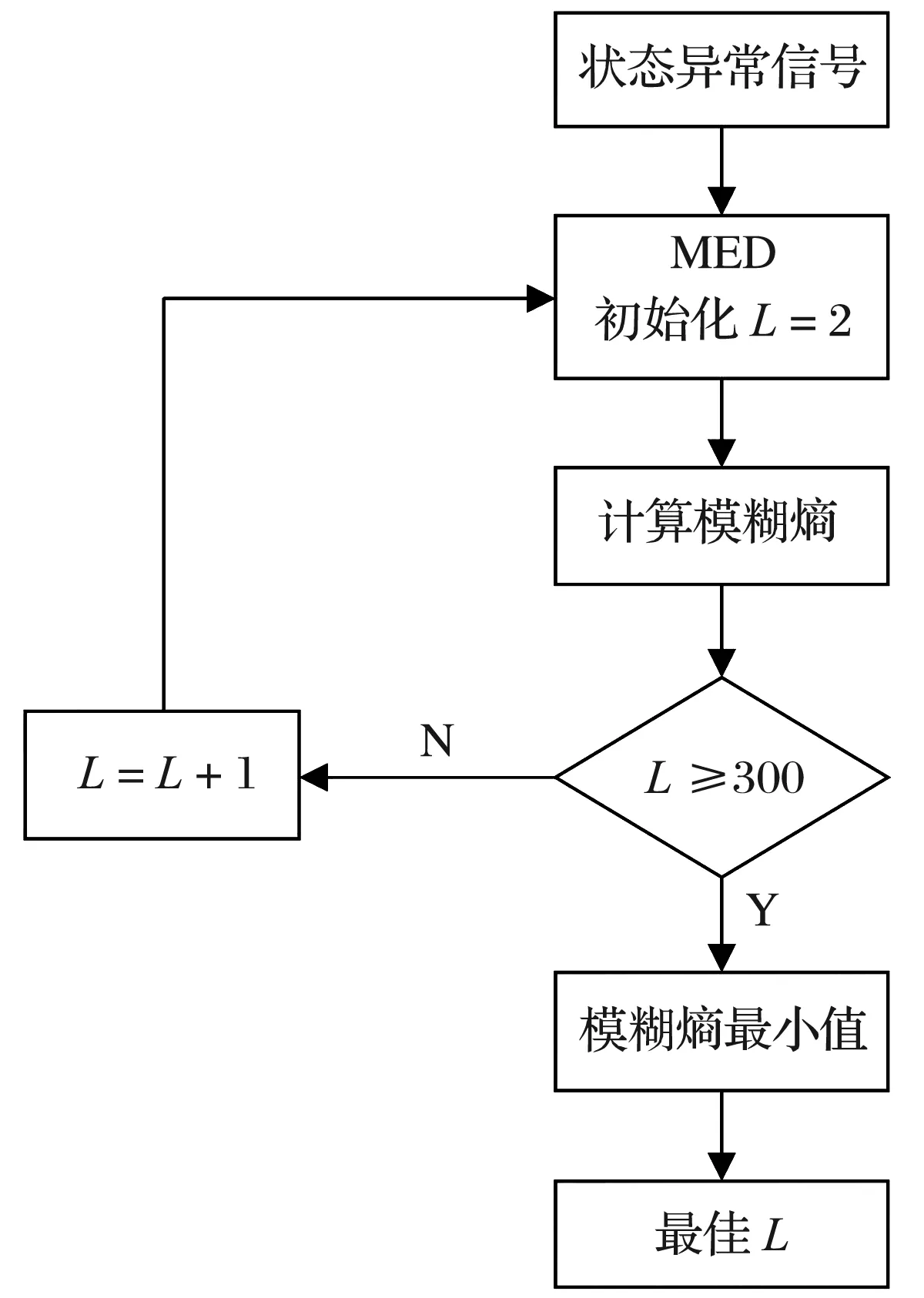
圖1 MED參數(shù)優(yōu)化流程圖Fig.1 Flow chart of MED parameter optimization

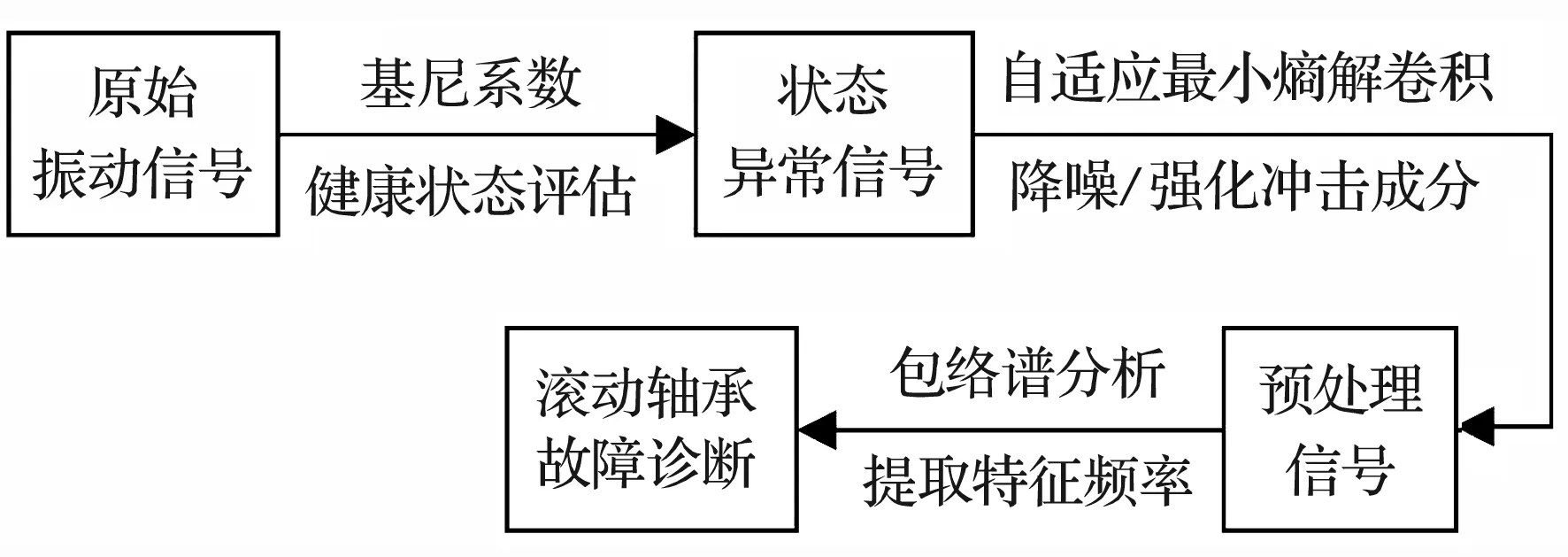
圖2 基于GI-AMED的滾動(dòng)軸承故障診斷流程Fig.2 Fault diagnosis process of rolling bearing based on GI-AMED

2 試驗(yàn)分析

采用美國(guó)辛辛那提智能維護(hù)中心的滾動(dòng)軸承全壽命數(shù)據(jù)[15]進(jìn)行分析，試驗(yàn)臺(tái)結(jié)構(gòu)如圖3所示，軸承與電動(dòng)機(jī)通過(guò)皮帶連接，每套軸承的水平和垂直方向各放置一個(gè)加速度傳感器采集數(shù)據(jù)。試驗(yàn)軸承型號(hào)為ZA-2115，轉(zhuǎn)速為2 000 r/min，具體參數(shù)見(jiàn)表1。選用發(fā)生外圈故障的1#軸承的數(shù)據(jù)進(jìn)行分析，每10 min采集一次數(shù)據(jù)，共得到984個(gè)數(shù)據(jù)。

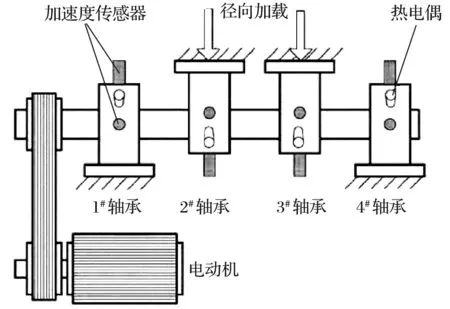
圖3 試驗(yàn)臺(tái)結(jié)構(gòu)示意圖Fig.3 Structure diagram of test bench

表1 ZA-2115軸承的基本參數(shù)Tab.1 Basic parameters of ZA-2115 bearing

1#軸承全壽命周期的運(yùn)行趨勢(shì)如圖4所示：在7 020 min時(shí)均方根值有明顯突變，表明軸承發(fā)生了故障[13]；基尼系數(shù)則從5 280 min開(kāi)始有上升趨勢(shì)，在7 020 min發(fā)生了更明顯的突變，判斷軸承產(chǎn)生故障；采用最小二乘法對(duì)軸承運(yùn)行狀態(tài)開(kāi)始變化的上升沿?cái)?shù)據(jù)進(jìn)行直線擬合，通過(guò)直線斜率K的對(duì)比可以看出，相對(duì)于均方根值，基尼系數(shù)對(duì)滾動(dòng)軸承運(yùn)行狀態(tài)的變化更敏感。

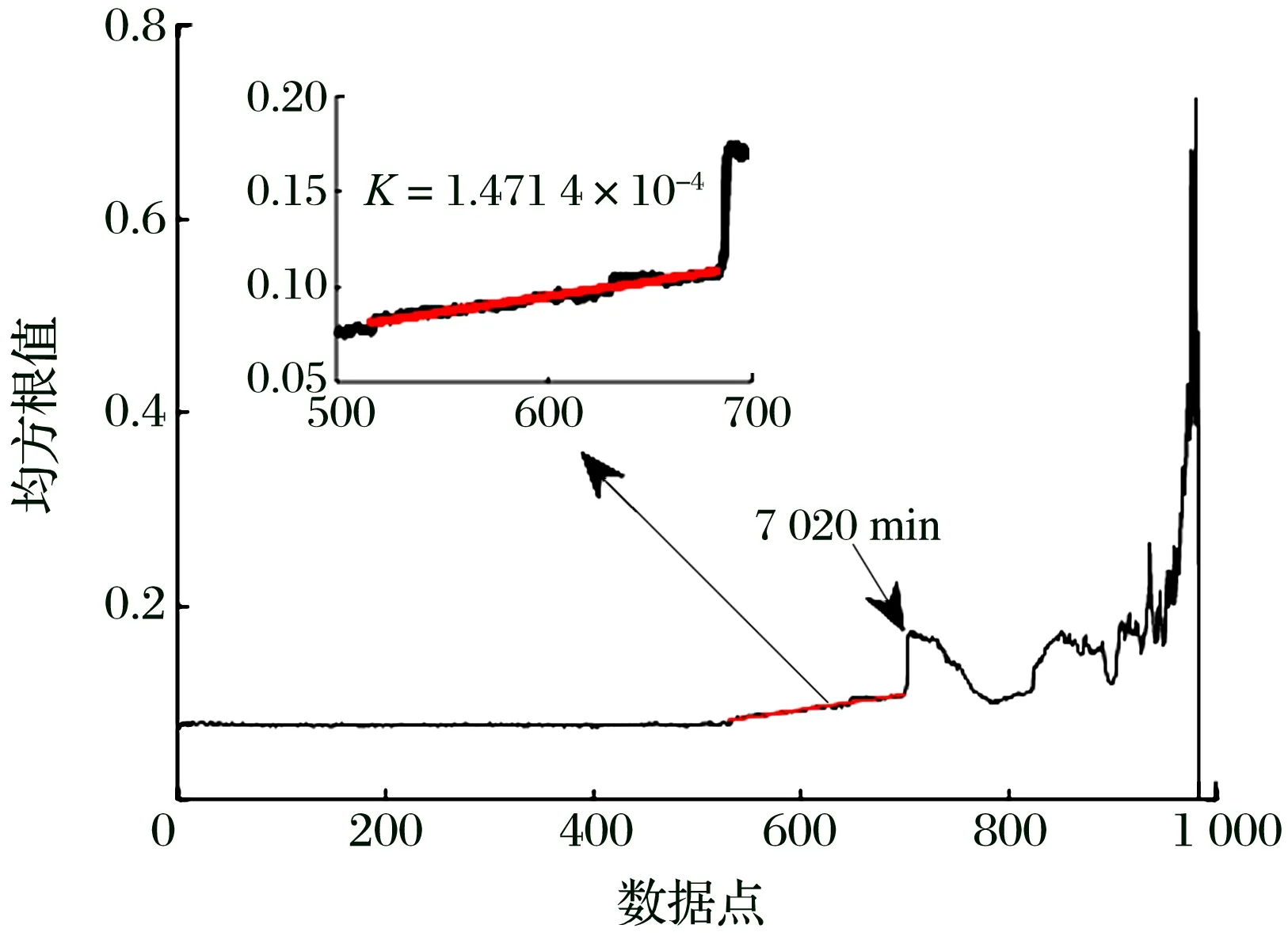
(a) 均方根值

為驗(yàn)證GI-AMED對(duì)軸承早期故障診斷的有效性，選取軸承狀態(tài)初始變化點(diǎn)(5 280 min)的振動(dòng)數(shù)據(jù)進(jìn)行分析，該時(shí)刻軸承振動(dòng)信號(hào)的時(shí)域波形及其包絡(luò)譜如圖5所示，包絡(luò)譜中存在較多干擾成分，觀察不到明顯的故障特征頻率。

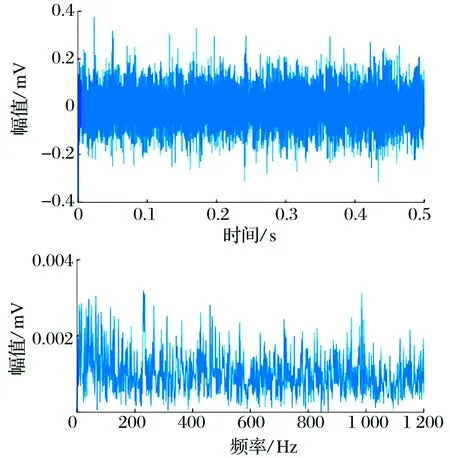
圖5 第5 280 min軸承振動(dòng)信號(hào)的時(shí)域波形與包絡(luò)譜Fig.5 Time-domain waveform and envelope spectrum of bearing vibration signals at 5 280 min

采用GI-AMED對(duì)第5 280 min軸承振動(dòng)信號(hào)進(jìn)行處理，通過(guò)模糊熵對(duì)最小熵解卷積的參數(shù)尋優(yōu)結(jié)果如圖6所示，利用AMED對(duì)軸承振動(dòng)信號(hào)進(jìn)行降噪處理的結(jié)果如圖7所示：從包絡(luò)譜中可以觀察到明顯的外圈故障特征頻率(230 Hz)及其倍頻，與發(fā)生明顯突變的第7 020 min相比提前了1 740 min實(shí)現(xiàn)軸承早期故障診斷。

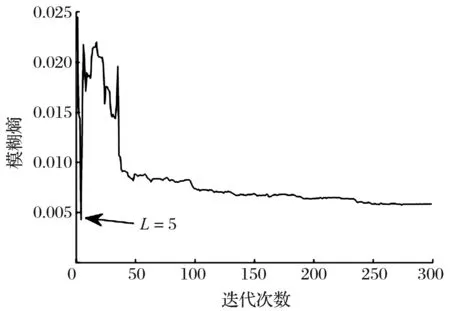
圖6 AMED濾波器長(zhǎng)度L的尋優(yōu)結(jié)果Fig.6 Optimization result of AMED filter length L

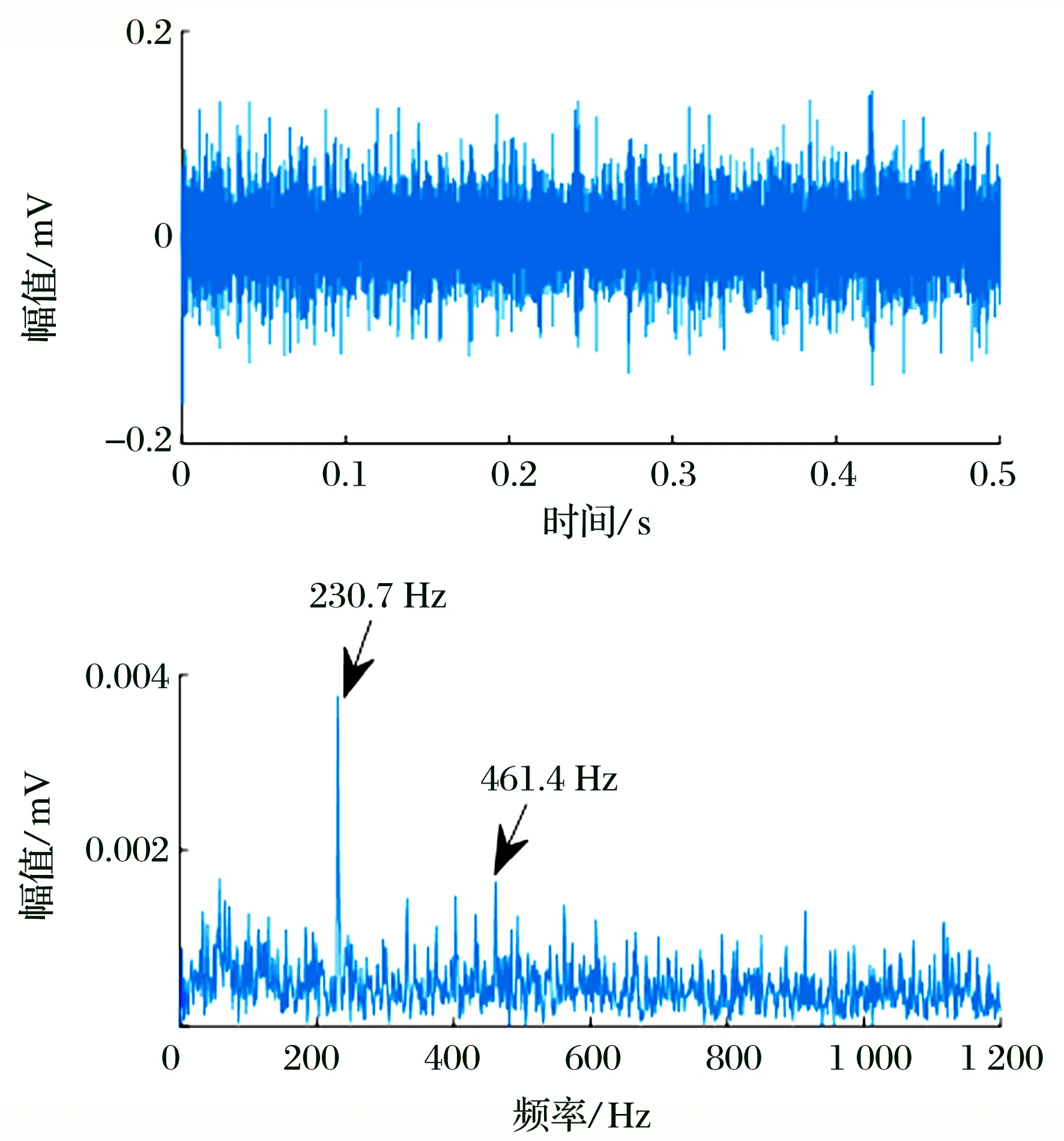
圖7 AMED降噪后的時(shí)域波形與包絡(luò)譜Fig.7 Time-domain waveform and envelope spectrum after AMED noise reduction

作為對(duì)比，文獻(xiàn)[7]采用最小熵解卷積與變分模態(tài)分解對(duì)5 370 min的軸承振動(dòng)數(shù)據(jù)進(jìn)行分析(圖8)，其依靠經(jīng)驗(yàn)選取MED濾波器長(zhǎng)度L為79，直接進(jìn)行包絡(luò)譜分析后只能識(shí)別故障特征頻率，但倍頻被干擾諧波淹沒(méi)，對(duì)降噪信號(hào)進(jìn)行變分模態(tài)分解后以峭度值為標(biāo)準(zhǔn)選取最優(yōu)分量進(jìn)行包絡(luò)譜分析才能識(shí)別出倍頻。而GI-AMED只需進(jìn)行包絡(luò)譜分析就可提取出故障特征頻率及其倍頻，且所處理數(shù)據(jù)提前了90 min采集，故障特征更加微弱，充分說(shuō)明了本文所提方法在滾動(dòng)軸承早期故障診斷中更具優(yōu)越性。

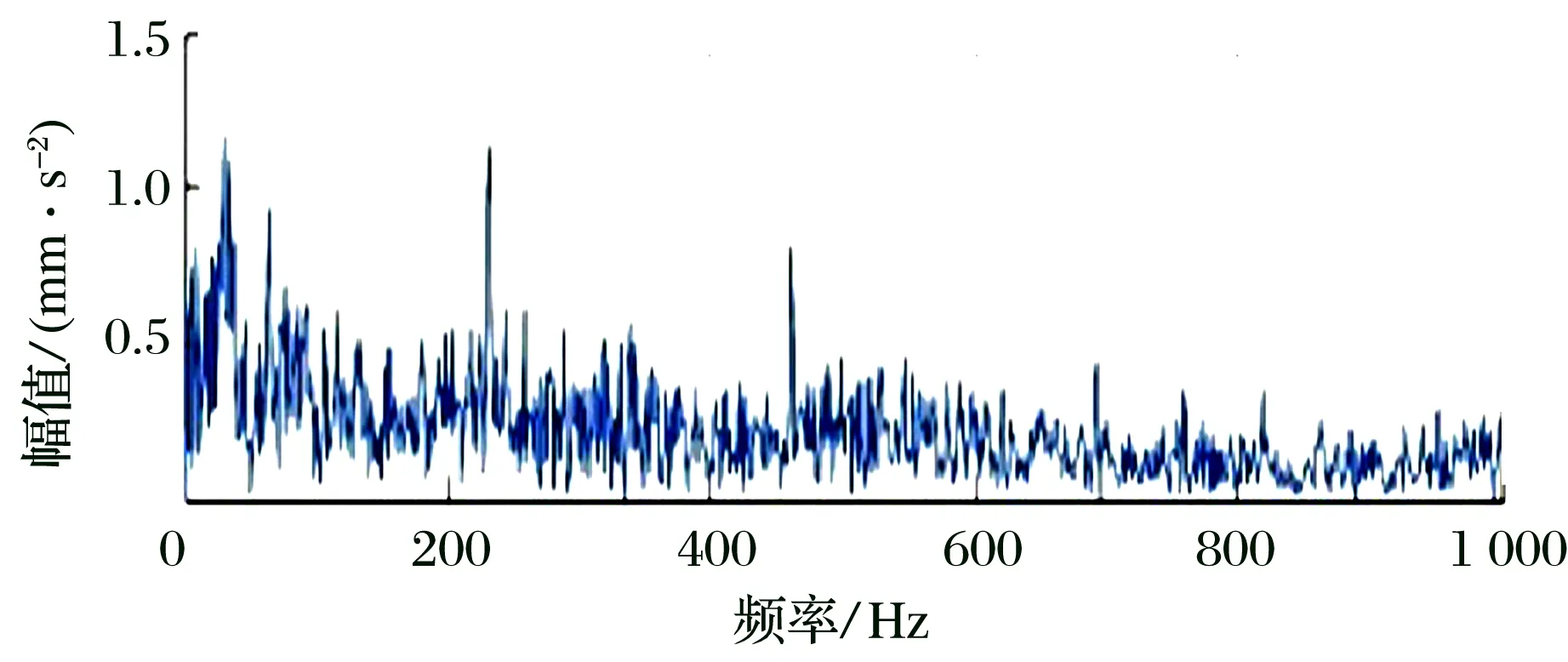
圖8 文獻(xiàn)[7]最優(yōu)分量IMF3的包絡(luò)譜Fig.8 Envelope spectrum of optimal component IMF3 in reference [7]

3 結(jié)束語(yǔ)

均方根值是軸承運(yùn)行趨勢(shì)常用的統(tǒng)計(jì)指標(biāo)，本文利用經(jīng)濟(jì)學(xué)中的基尼系數(shù)對(duì)軸承全壽命周期數(shù)據(jù)進(jìn)行處理，與均方根值擬合直線斜率的定量對(duì)比證實(shí)了基尼系數(shù)是一種更優(yōu)越的指標(biāo)。利用模糊熵對(duì)最小熵解卷積的參數(shù)L進(jìn)行尋優(yōu)，克服了人為經(jīng)驗(yàn)選取的局限性，對(duì)比分析結(jié)果也表明其降噪效果更好，GI-AMED方法能夠更好地實(shí)現(xiàn)滾動(dòng)軸承早期微弱故障的有效判定。