基于滑動窗口一維卷積自編碼器的滾動軸承故障實時診斷

趙耀，仲志丹，田恒，謝興會，程永龍

(1.河南科技大學 機電工程學院，河南 洛陽 471003；2.航空精密軸承國家重點實驗室，河南 洛陽 471039；3.中鐵工程裝備集團有限公司，鄭州 450016)

滾動軸承是機械設備的重要基礎部件，也是易損部件[1]，軸承故障是常見的機械設備故障，在一些情況下會導致機械設備的損壞并危及生命財產安全，因此，軸承故障診斷方法的智能化和精準化成為研究的新目標[2]。通常，對軸承信號進行時域、頻域、時頻域分析以診斷故障類型，如小波包變換、經驗小波變換[3]、快速傅里葉變換[4]等，但這些方法依賴于專家經驗且需人為分析信號并提取重要特征，整個過程十分繁瑣，診斷效果也有待進一步提高[5]。

近年來，隨著計算機性能的大幅提高和傳感器技術的高速發展，依賴于機械設備的海量傳感器數據，基于深度學習的故障診斷方法繁榮開展，與依賴人為經驗提取特征不同，深度學習方法以強大的自適應能力自發提取故障特征，而且識別能力大大提升[6]。自編碼器屬于深度學習中的無監督方法，文獻[7]利用堆疊式自編碼器構建深度學習網絡，其利用訓練集訓練自編碼器獲得隱含向量，然后將輸出層去除并將隱含向量輸入下一個自編碼器中，成功診斷滾動軸承故障，但網絡中的計算單元為最基本的神經元，計算能力有待提高。卷積神經網絡是經典的有監督算法，其計算單元為卷積核，比普通神經網絡的計算能力更高效[8]：文獻[9]將軸承時域振動信號轉化為小波時頻圖后再輸入二維卷積神經網絡進行故障診斷，但仍然受人工特征提取的干擾，并不能完全發揮卷積神經網絡的強大學習能力；文獻[10]直接以原始時域信號作為一維卷積神經網絡的輸入，不涉及任何人工特征提取的計算，成功診斷了軸承故障。相較于二維卷積，一維卷積可直接處理原始時域信號，不涉及人工特征提取的干擾，可充分利用卷積網絡的學習能力。

為自適應的提取特征，避免人工參與帶來的失誤，發揮不同網絡的優勢，本文提出了一種基于滑動窗口一維卷積自動編碼器(SW1DCAE)的滾動軸承無監督故障檢測算法，使用無監督方式預訓練網絡模型，通過重用編碼層結構，使用少量標簽數據訓練分類器即可完成軸承故障診斷。

1 理論背景

單純采用卷積神經網絡進行故障診斷屬于有監督學習，網絡模型的準確率極大依賴于標簽數據的數量；而自編碼器等無監督方法的網絡連接方式多為全連接神經元，計算能力不足：因此，以自編碼器為基礎架構，以卷積核為基本計算單元，構建融合不同網絡優勢的卷積自編碼器，以使用少量標簽訓練分類器并進行故障診斷。

1.1 自編碼器

自動編碼器能夠學習輸入信息的隱含特征并將其重構，可分為編碼和解碼2個步驟，其網絡結構如圖1所示。

圖1 自編碼器網絡結構Fig.1 Structure of auto-encoder network

對于第m個輸入信號

(1)

其編碼過程為

Hm=σ0(W0Xm+b0) ，

(2)

解碼過程為

(3)

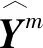
ReLU激活函數的表達式為

σ=max(0,x) ，

(4)

損失函數為

(5)

1.2 卷積神經網絡

一維卷積神經網絡通常由卷積層、池化層、全連接層組成，其網絡結構如圖2所示。

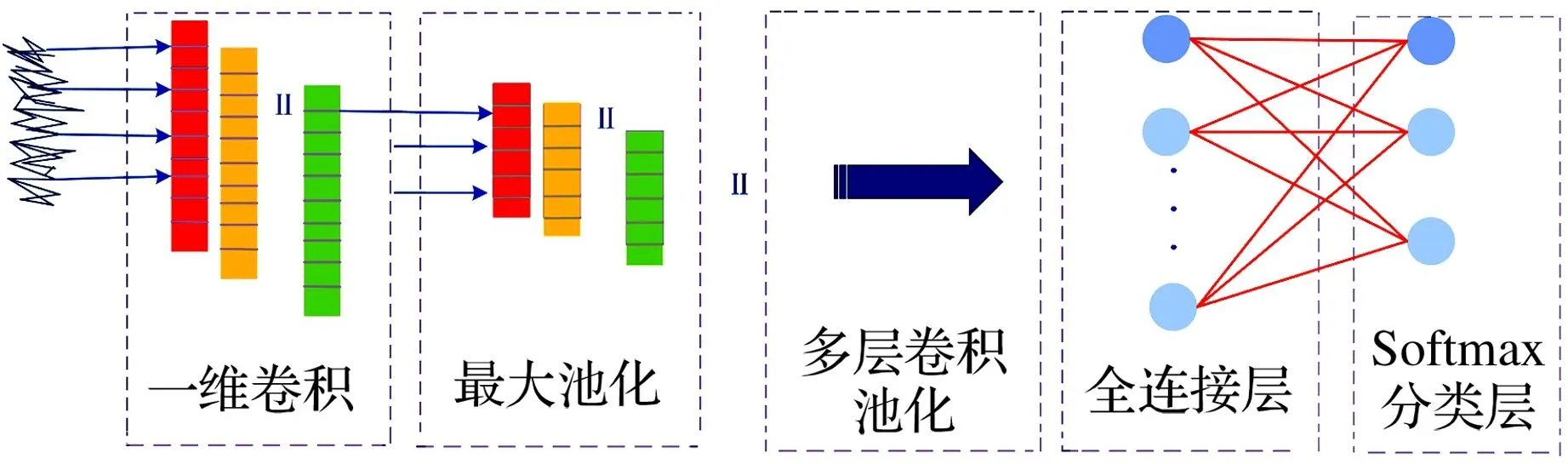
圖2 一維卷積神經網絡結構Fig.2 Structure of one-dimensional convolutional neural network

卷積層由卷積核構成，卷積核可進行一維卷積計算，其輸出為

(6)

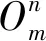
池化層選用最大池化以減小特征面的維度和訓練的成本，其輸出為

p=max (O1,O2,O3,…,On)，

(7)

式中：n為池化區域的寬度；Oi為池化區域的第i個數據。

全連接層在卷積和池化之后，其輸出為

δ=f(ωP+b)，

(8)

式中：ω為權重；b為偏差；f為激活函數；P為輸入。

1.3 滑動窗口算法

如圖3所示，滑動窗口通過指定一個固定長度的窗口去框住時間序列，并以固定的長度和步長朝著指定方向前進，可以得到任一個窗口數據的均值、方差等信息。

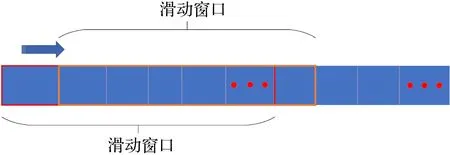
圖3 滑動窗口算法示意圖Fig.3 Diagram of sliding window algorithm

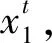
2 滑動窗口一維卷積自編碼器模型

2.1 節點隨機丟棄技巧

在常規神經網絡中，神經元之間復雜的共適應關系會導致過擬合的發生，節點隨機丟棄技巧(Dropout)[11]可以對神經元節點進行隨機舍棄，被丟棄的神經元不再參與計算，減弱了神經元的共適應關系以及節點間的相關性，從而防止網絡訓練過擬合。因此，本文引入Dropout，在神經元節點處添加一道概率流程使之隨機丟棄，以防止網絡過擬合的發生，網絡結構如圖4所示。

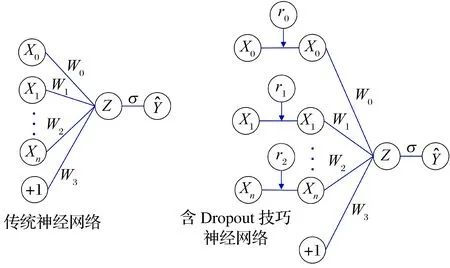
圖4 節點隨機丟棄技巧Fig.4 Node random discard technique

不存在Dropout的網絡的計算公式為

(9)

(10)

采用Dropout的網絡，其節點處存在一道概率流程，輸入的計算公式為

(11)

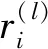
2.2 網絡模型的搭建

一維卷積自編碼器將卷積計算引入傳統的自編碼器，通過卷積、池化、反卷積提取數據的隱含特征，其結構如圖5所示。

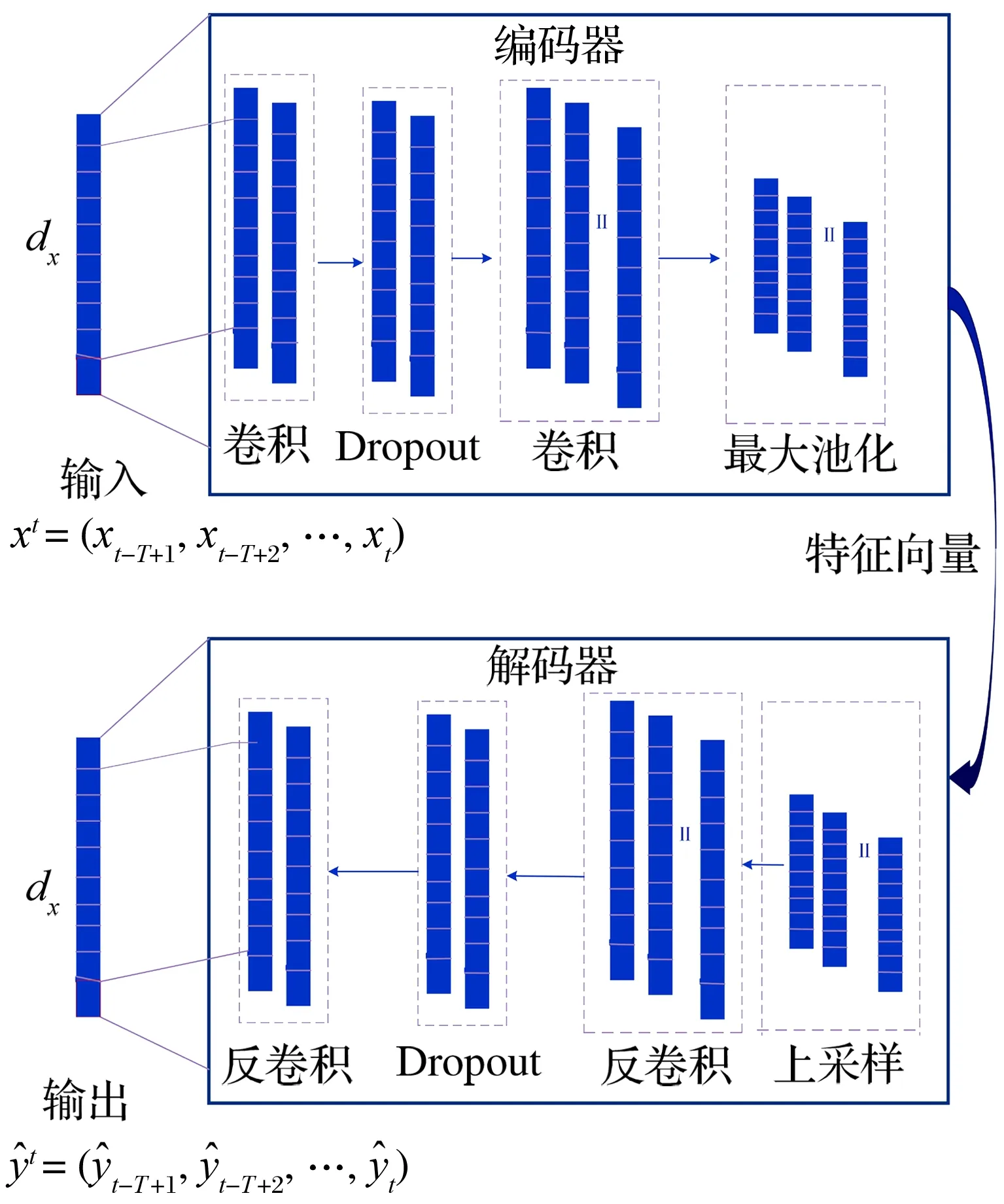
圖5 一維卷積自編碼器模型Fig.5 One-dimensional convolutional auto-encoder model

SW1DCAE模型分為數據處理、編碼和解碼3個階段。數據處理階段，通過滑動窗口算法將長時間序列截取為若干段短時間序列并生成訓練樣本，以便網絡更好地捕獲數據的序列相關性。假設時間步長為T(窗口的長度)，窗口中的觀測數據有維度dx，每個輸入數據具有維度(T，dx)。

編碼器由一維卷積層、Dropout層、一維池化層構成，卷積層和池化層對數據編碼以找到隱含特征，對于第i個卷積核，其輸出為

Ci=ReLU(∑Xωi+bi)，

(12)

Dropout層可有效防止過擬合，池化后數據維度減半，輸出為

(13)

式中：s為池化步長；W為池化窗口大小。本文中兩者取值均為2。

解碼器由反卷積層、上采樣層、Dropout層構成，第1層為采樣層，用于恢復數據維度，其輸出為

(14)

反卷積層是卷積層的逆運算，第i個通道的輸出為

Di=ReLU(∑X?ωi+bi) ，

(15)

式中：jk為池化時記錄的最大值的位置；ωi為反卷積核；?為反卷積運算。

相較于3σ準則，箱線圖法以四分位數和四分位距為基礎，無需對數據進行假設分布，有更好的魯棒性。因此，采用箱線圖法進行異常判定，如圖6所示。

圖6 異常判定的箱線圖法Fig.6 Boxplot diagram method for anomaly determination

利用箱線圖法判定異常時，處于上下邊緣之外的數據為異常點位，上、下邊緣分別為

(16)

異常判定根據為

(17)

式中：Q3為正常狀態下Loss分布的上四分位數；Q1為正常狀態下Loss分布的下四分位數；dIQR為四分距；LLOSS為樣本通過SW1DCAE模型產生的損失值。

2.3 模型訓練與優化

SW1DCAE模型通過重構輸入信號學習隱含特征，網絡模型取MSE作為損失函數，即

(18)

通過梯度下降法優化網絡模型參數，對于卷積層，梯度為

(19)

式中：xi為輸入；C為輸出；為卷積運算；flip表示矩陣的轉置。

對于最大池化，梯度為

(20)

式中：x為輸入；P為輸出。

對于上采樣層，梯度為

(21)

式中：xi為第i個輸入；Ut為第t個輸出；k為上采樣的步長。

對于反卷積層，梯度為

(22)

(23)

式中：K(j)為第j個反卷積核；x為輸入；D為輸出；m為反卷積的步長；k=0,1,…,t；t為輸入x的長度。

SW1DCAE模型的訓練和測試流程如圖7所示。

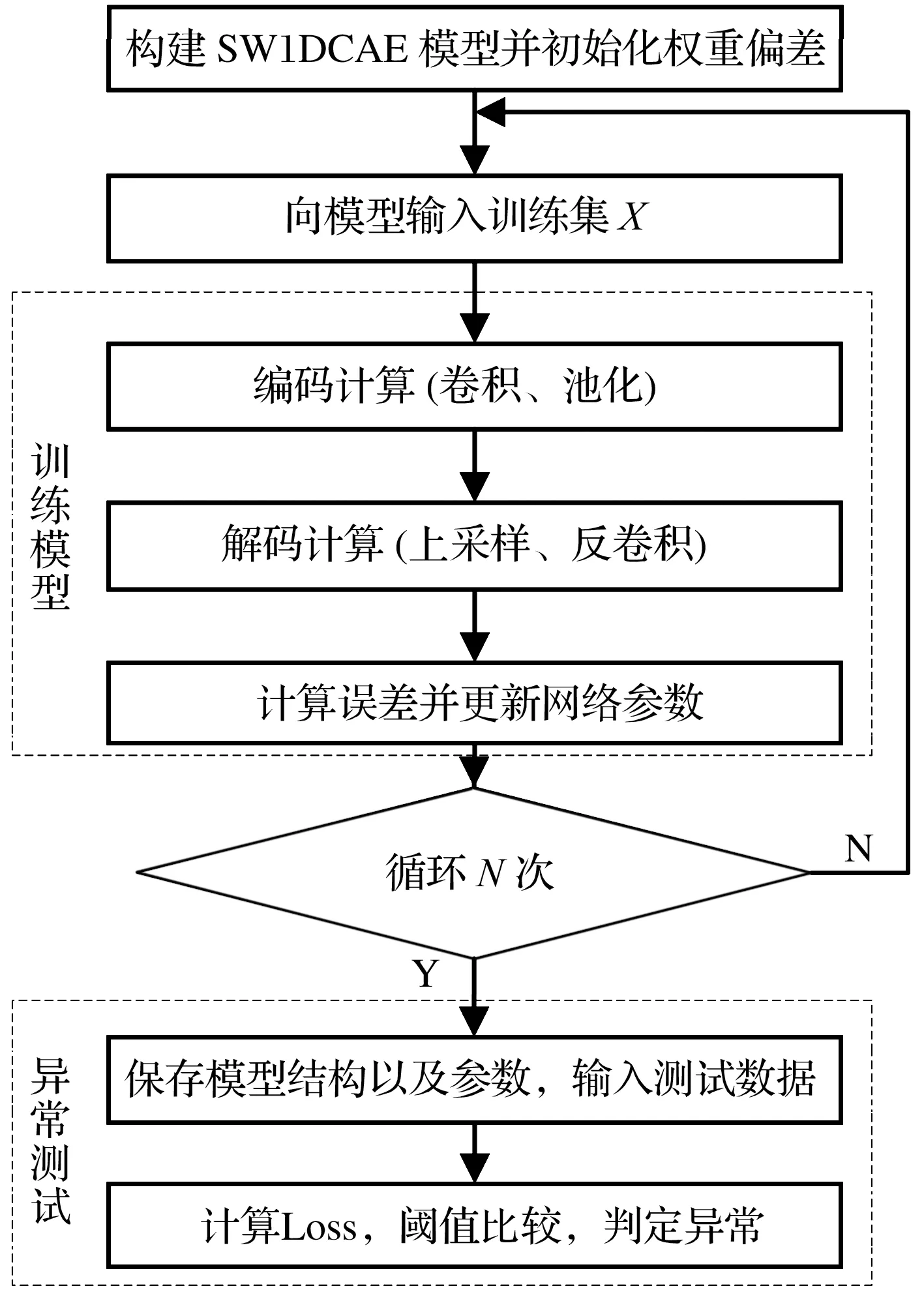
圖7 SW1DCAE模型的訓練和異常測試流程Fig.7 Training and abnormal testing process of SW1DCAE model

2.4 基于SW1DCAE的故障分類器

通過預訓練SW1DCAE模型獲取特征提取器(編碼層結構)。故障診斷時采用預訓練SW1DCAE模型的編碼層結構與權重，與全連接層和Softmax分類層共同構建分類器。基于SW1DCAE的軸承故障分類算法如圖8所示，異常檢測和故障診斷的整體流程如圖9所示

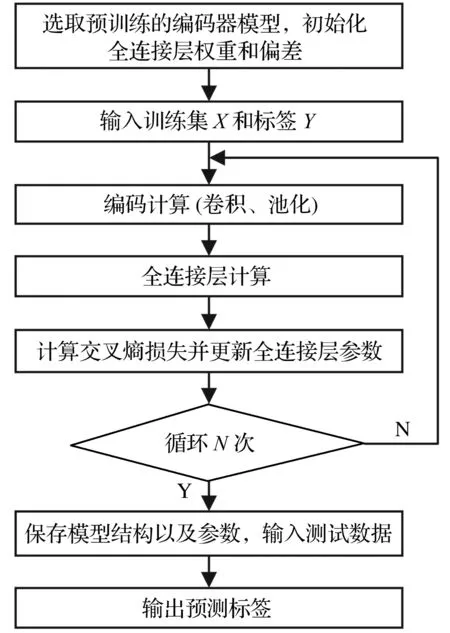
圖8 基于SW1DCAE模型的故障分類Fig.8 Fault classification based on SW1DCAE model

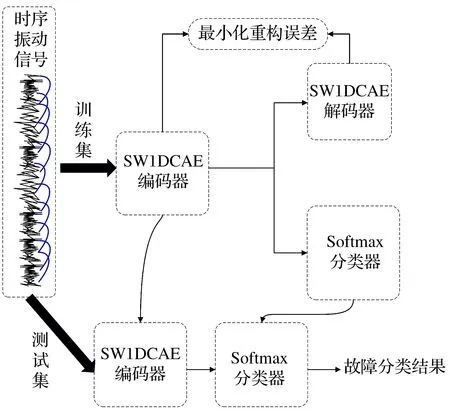
圖9 基于SW1DCAE的故障診斷流程Fig.9 Flow chart for fault diagnosis based on SW1DCAE

3 試驗分析

為驗證本文提出的滑動窗口一維卷積自動編碼器模型的性能，使用西儲大學軸承數據集進行驗證。

3.1 滑動窗口敏感性分析

滑動窗口的長度是模型能否有效獲取數據特征的重要因素，而且關系到計算成本，在一定程度上影響著模型的性能。在文中所提網絡結構參數下，滑動窗口長度在200～450變化期間，SW1DCAE模型的故障分類準確率和檢測時間如圖10所示：滑動窗口長度為400時，模型的準確率較好(約0.990)，隨著滑動窗口長度的增加，檢測時間不斷增加，意味著訓練成本不斷升高，而準確率則不再上升。因此，不宜選取太長的滑動窗口，本文選取滑動窗口長度為400進行重構及故障分類性能分析。

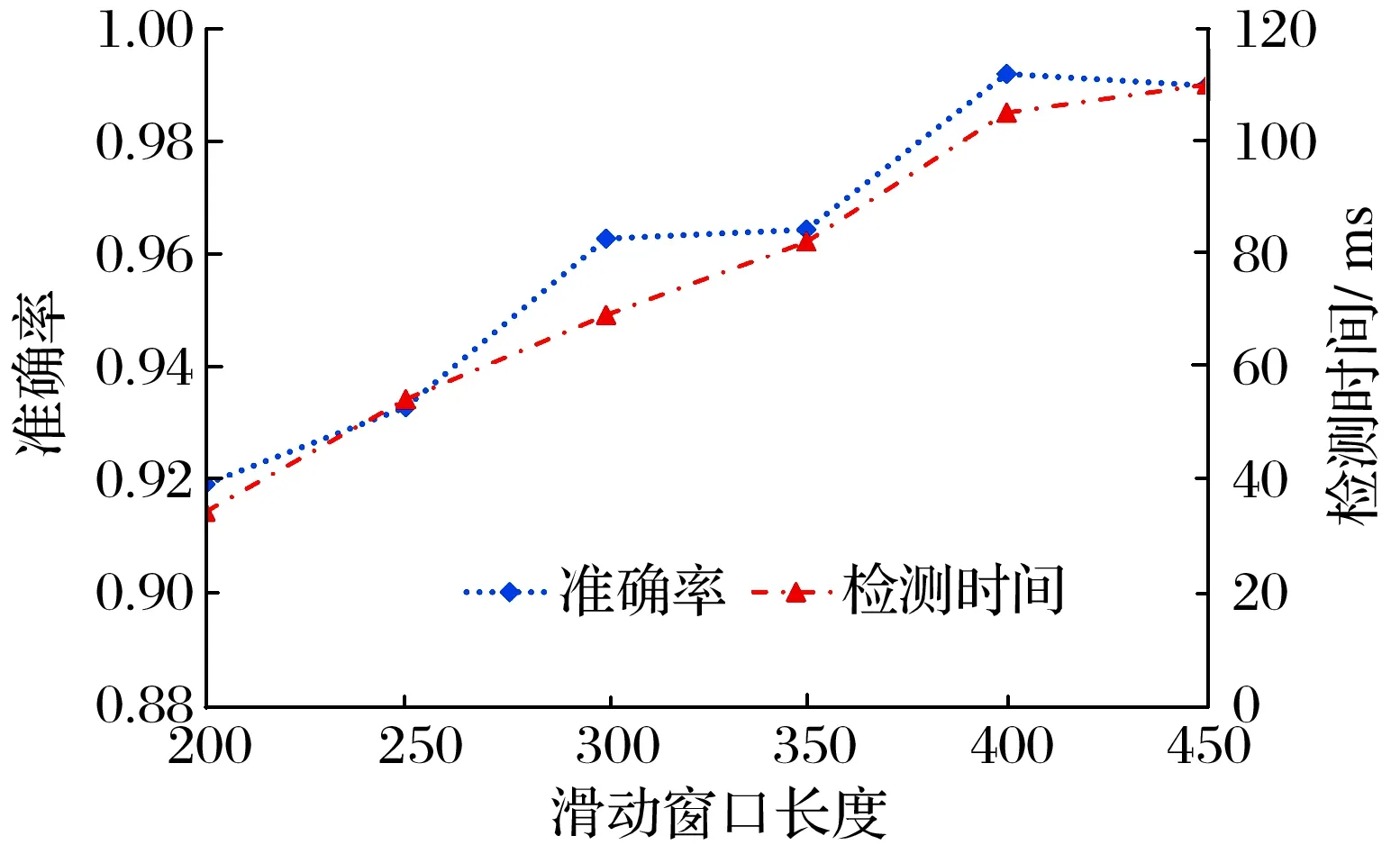
圖10 滑動窗口長度對SW1DCAE模型性能的影響Fig.10 Effect of sliding window length on performance of SW1DCAE model

3.2 SW1DCAE重構性能分析

選擇48 kHz采樣頻率下，驅動端SKF 6205軸承的正常數據作為訓練集，滾動體故障數據作為測試集。試驗期間，將滑動窗口的大小設置為400，Dropout層參數設置為0.5，Batch-size為256，Adam優化器中的初始學習率為0.001， SW1DCAE異常檢測模型的網絡結構見表1。

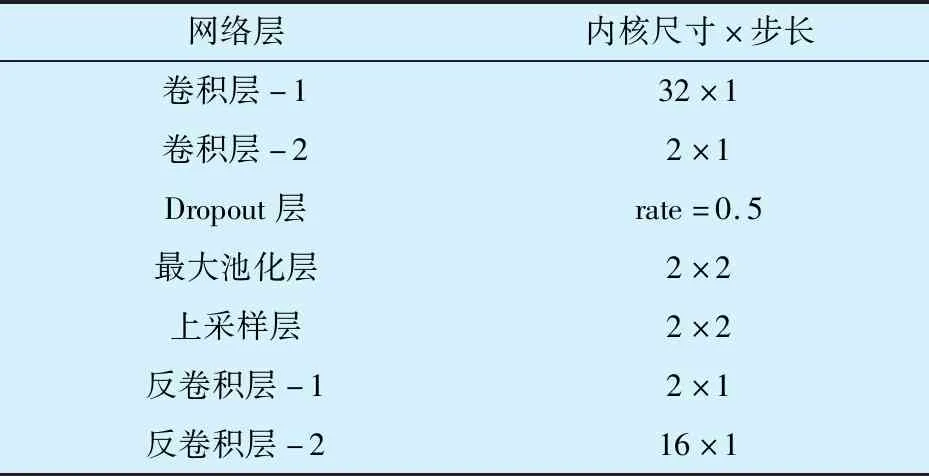
表1 SW1DCAE異常檢測模型的網絡結構Tab.1 Network structure of SW1DCAE anomaly detection model

編碼器部分，第1層卷積選取了比較寬的卷積核以更好地提取特征；池化層選取窗口尺寸為2，步長為2，在保留重要特征的情況下有效降低數據維度。解碼器部分，上采樣層、反卷積層的參數設置與編碼器部分相同。

訓練期間的損失函數如圖11所示，可以看出訓練集與驗證集的均方誤差MSE隨著迭代次數的增加而逐步下降，訓練效果良好。

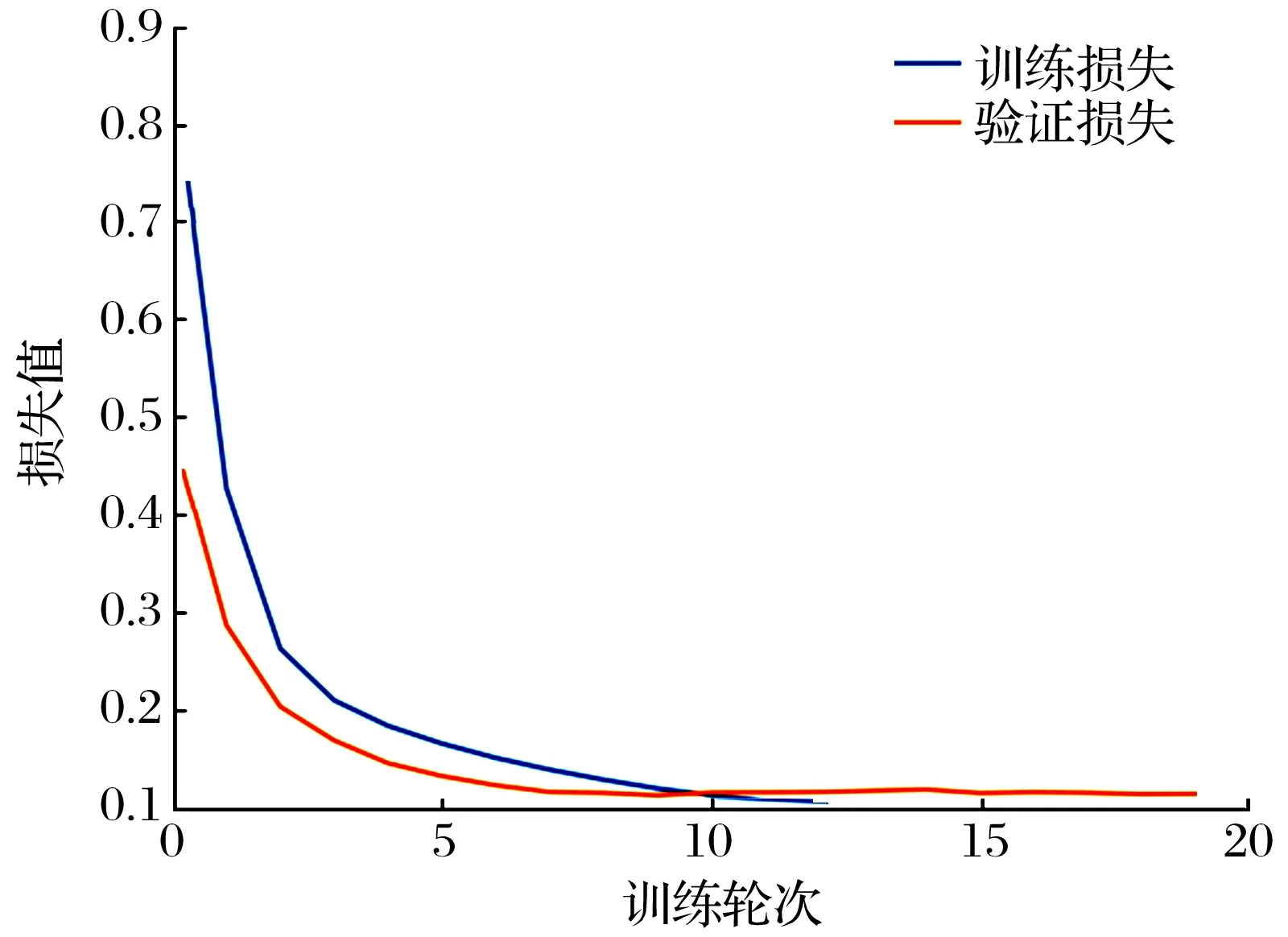
圖11 訓練集和驗證集的損失函數Fig.11 Loss function of training set and verification set

SW1DCAE模型對正常信號的重構效果如圖12所示，結果表明SW1DCAE模型能夠有效重構輸入信號，性能良好。

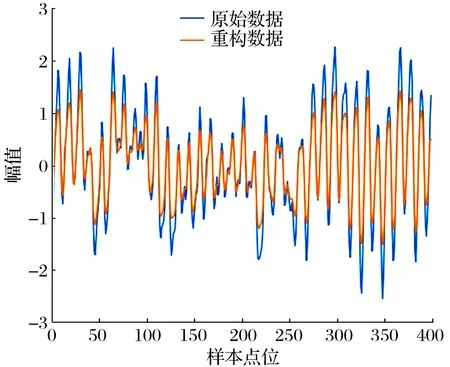
圖12 信號重構圖Fig.12 Diagram of signal reconstruction

3.3 SW1DCAE分類性能分析

選擇48 kHz采樣頻率下，驅動端SKF 6205軸承0 HP工況下的 10 種軸承故障信號作為研究對象，對SW1DCAE故障分類模型進行驗證，網絡結構見表2。

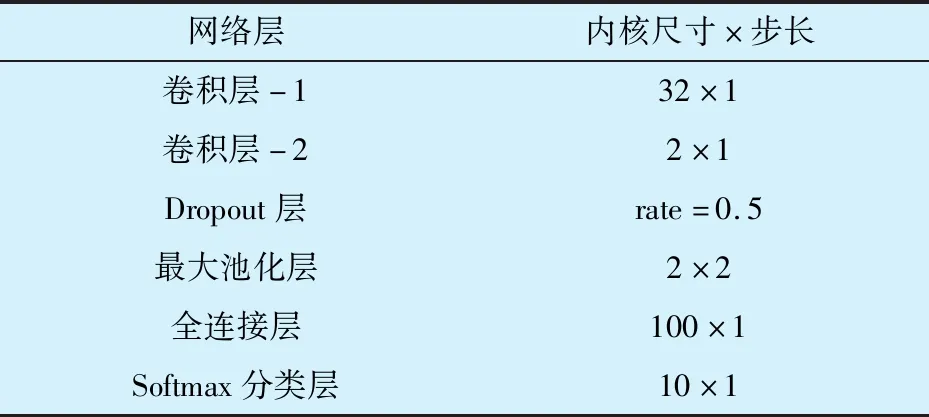
表2 SW1DCAE故障分類模型的網絡結構Tab.2 Network structure of SW1DCAE fault classification model

使用t-SNE對學習的特征進行降維并可視化處理，結果如圖13所示：隨著網絡層的加深，相同標簽的特征數據逐漸產生很好的分類效果。

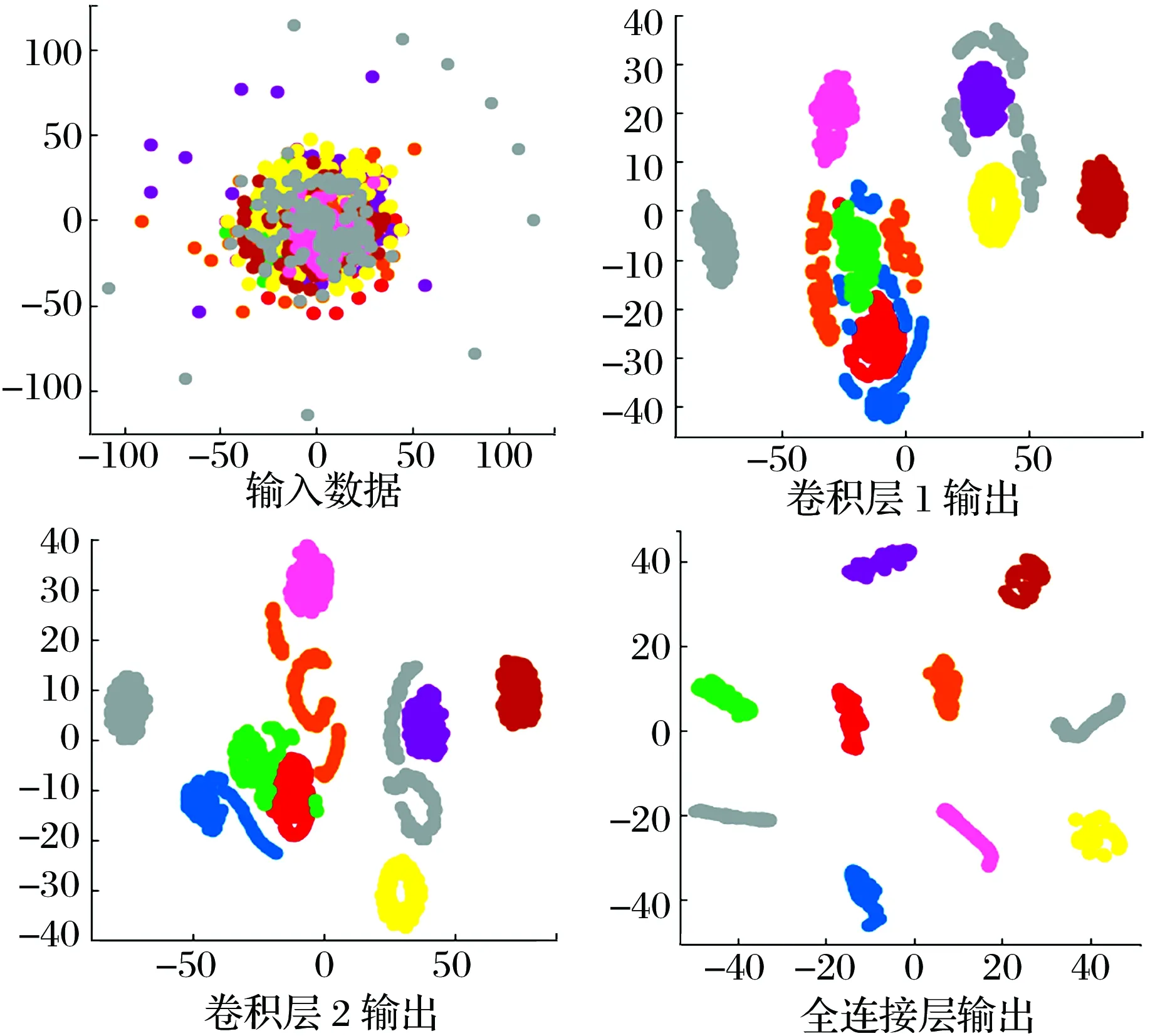
圖13 分類過程的可視化Fig.13 Visualization of classification process

為進一步證明SW1DCAE分類模型的優越性，與AE模型(在傳統自編碼器的編碼層后連接Softmax分類層構成分類器)和CNN模型(卷積神經網絡進行故障分類)進行對比試驗，結果見表3：SW1DCAE分類模型的訓練準確率和測試準確率均優于普通自編碼器以及單一卷積神經網絡。SW1DCAE能夠直接從原始信號提取特征并重構信號，將卷積神經網絡、自編碼器、滑動窗口結合為一體，從而在軸承故障檢測中表現出良好的性能。

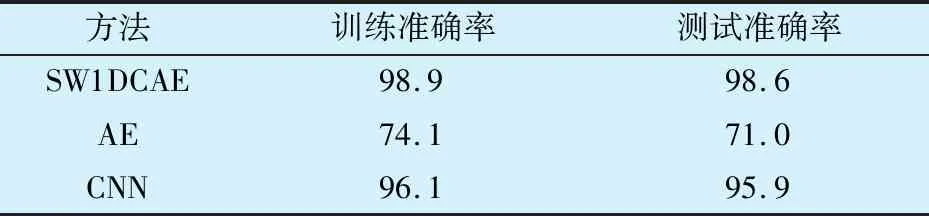
表3 不同方法的分類準確率Tab.3 Classification accuracy of different methods %

此外，SW1DCAE模型占用內存小，運算速度快，能夠運行在嵌入式計算機上，可廣泛應用于邊緣計算故障診斷領域。

4 結束語

本文提出了基于SW1DCAE的滾動軸承故障檢測方法，并通過西儲大學軸承數據集驗證該方法的優越性和可行性，其具備以下特性：

1)引入滑動窗口算法，將原始數據塑造成合適長度的樣本，能夠更好地捕獲數據的序列相關性；

2)將一維卷積核作為計算單元引入自編碼器提取數據特征，能夠提高模型的異常檢測性能。

3)相比于其他算法，SW1DCAE模型不需要太多的軸承先驗知識，無需標簽數據和人為提取特征，而且占用內存小，運算速度快，能夠運行在嵌入式計算機上，可廣泛應用于邊緣計算等智能故障診斷領域。

在實際工程中，機械設備中的軸承型號眾多，工況條件也有所不同，因此軸承的振動信號也具有不同的特性，導致同一故障診斷模型無法以高準確度匹配多種情況，如何通過遷移學習使同一模型在不同環境、工況中快速精準適配，是值得繼續研究的內容。