外圈與軸承座間隙對滾道故障軸承振動性能的影響

劉明輝，耿濤，曲瓊，閆淑萍，王風(fēng)濤

(1.洛陽LYC軸承有限公司，河南 洛陽 471039；2.航空精密軸承國家重點實驗室，河南 洛陽 471039；3.河南省高端軸承產(chǎn)業(yè)研究院，河南 洛陽 471039；4.安徽工程大學(xué) 機(jī)械工程學(xué)院，安徽 蕪湖 241000)5.河南省軸承技術(shù)創(chuàng)新中心，河南 洛陽 471039；

由于承載能力強(qiáng)，摩擦阻力小，結(jié)構(gòu)緊湊等優(yōu)點，圓柱滾子軸承被廣泛用作機(jī)械系統(tǒng)的關(guān)鍵支承部件， 其工作性能直接影響機(jī)械系統(tǒng)的運行狀態(tài)。受運行工況影響， 滾子與滾道極易發(fā)生接觸疲勞，出現(xiàn)表面剝落， 嚴(yán)重影響圓柱滾子軸承的工作性能，甚至引發(fā)機(jī)械系統(tǒng)的災(zāi)難性事故：因此，需要通過故障診斷方法發(fā)現(xiàn)并確定圓柱滾子軸承局部故障。

滾動軸承故障診斷理論依據(jù)來源于其振動性能，為此，眾多學(xué)者針對滾動軸承故障振動性能進(jìn)行了詳細(xì)研究：文獻(xiàn)[1-3]分別采用方波、三角波和半正弦波信號描述故障沖擊，構(gòu)建故障軸承振動模型，分析了徑向載荷和軸向載荷耦合作用下外滾道、內(nèi)滾道和滾動體的振動頻率；文獻(xiàn)[4]采用隨機(jī)點描述故障產(chǎn)生的激發(fā)力，融入隨機(jī)模型構(gòu)建故障軸承分析模型，分析了振動信號的頻譜特征；文獻(xiàn)[5]提出了基于時變交替載荷作用下轉(zhuǎn)子軸承動力學(xué)系統(tǒng)的故障分析模型；文獻(xiàn)[6-7]采用彈簧模型研究了包含局部故障的齒輪-轉(zhuǎn)子-軸承系統(tǒng)的振動特性；文獻(xiàn)[8]研究了包含滾動體故障和滾道故障軸承的非線性動力學(xué)特征；文獻(xiàn)[9]對故障尺寸和位置對球軸承振動性能的影響進(jìn)行了研究；文獻(xiàn)[10]采用半正弦函數(shù)和矩形函數(shù)描述時變局部故障，對故障球軸承的振動特性進(jìn)行分析；文獻(xiàn)[11]綜合考慮軸承徑向游隙、載荷分布、幾何尺寸等因素，分析了外滾道出現(xiàn)損傷后軸承的振動響應(yīng)；文獻(xiàn)[12]通過考慮環(huán)境噪聲的影響建立了內(nèi)滾道出現(xiàn)局部故障時軸承的分析模型；文獻(xiàn)[13]建立了一個平面動力學(xué)分析模型對故障軸承的振動響應(yīng)進(jìn)行分析；文獻(xiàn)[14-15]對內(nèi)滾道和外滾道存在局部故障時軸承的振動響應(yīng)進(jìn)行了分析；文獻(xiàn)[16]基于拉格朗日方程建立了齒輪箱-軸承系統(tǒng)的非線性動力學(xué)分析模型，分析了滾道和滾動體局部故障對系統(tǒng)非線性振動的影響；文獻(xiàn)[17]對復(fù)合故障下滾動軸承的振動特性進(jìn)行了分析；文獻(xiàn)[18-19]采用有限元方法對軸承系統(tǒng)進(jìn)行建模，通過在故障對應(yīng)節(jié)點上施加連續(xù)的沖擊力分析了故障軸承的振動響應(yīng)及不平衡力的影響；文獻(xiàn)[20-21]采用ADAMS軟件研究了存在局部故障深溝球軸承的動力學(xué)行為，該模型考慮了油膜厚度和油膜阻尼等對軸承振動響應(yīng)的影響；文獻(xiàn)[22]采用多體動力學(xué)鍵合圖法構(gòu)建了球軸承三維運動動力學(xué)模型，通過改變表面幾何特征對局部表面故障進(jìn)行了模擬；文獻(xiàn)[23]基于Gupta軸承動力學(xué)模型分析了滾道局部故障對軸承振動性能的影響；文獻(xiàn)[24]研究了滾子局部故障對軸承振動的性能影響。

由上述文獻(xiàn)可知，現(xiàn)有故障軸承振動分析模型大多將外圈與軸承座固定為一體；然而，受工作環(huán)境溫度或載荷影響，軸承外圈與軸承座間易出現(xiàn)間隙，直接影響故障軸承的振動特征，嚴(yán)重影響軸承故障診斷結(jié)果的精確性：因此，為分析軸承外圈與軸承座間隙對圓柱滾子軸承振動性能的影響規(guī)律，構(gòu)建考慮間隙影響的軸承故障振動分析模型，為滾動軸承故障精細(xì)化診斷提供理論依據(jù)。

1 滾道故障軸承動力學(xué)建模

考慮圓柱滾子軸承的結(jié)構(gòu)特性，為建立有效的動力學(xué)模型，提高計算效率，進(jìn)行以下假設(shè)：各零件的質(zhì)心與形心重合且只存在局部彈性變形，所有零件只在平面內(nèi)運動，忽略熱效應(yīng)影響。以上述假設(shè)為基礎(chǔ)，構(gòu)建滾子與滾道作用關(guān)系模型、滾道故障模型、外圈與軸承座作用關(guān)系模型和軸承系統(tǒng)動力學(xué)方程，形成考慮外圈與軸承座間隙的圓柱滾子軸承滾道故障分析模型。

1.1 滾子與滾道作用關(guān)系模型

如圖1所示，建立慣性坐標(biāo)系Oxyz，滾子定體坐標(biāo)系Obxbybzb，滾子方位坐標(biāo)系Obxayaza，外圈定體坐標(biāo)系Orxryrzr。慣性坐標(biāo)系中滾子中心位置向量為rb，外圈中心位置向量為rr，則外圈定體坐標(biāo)系中滾子中心到外圈中心的距離為

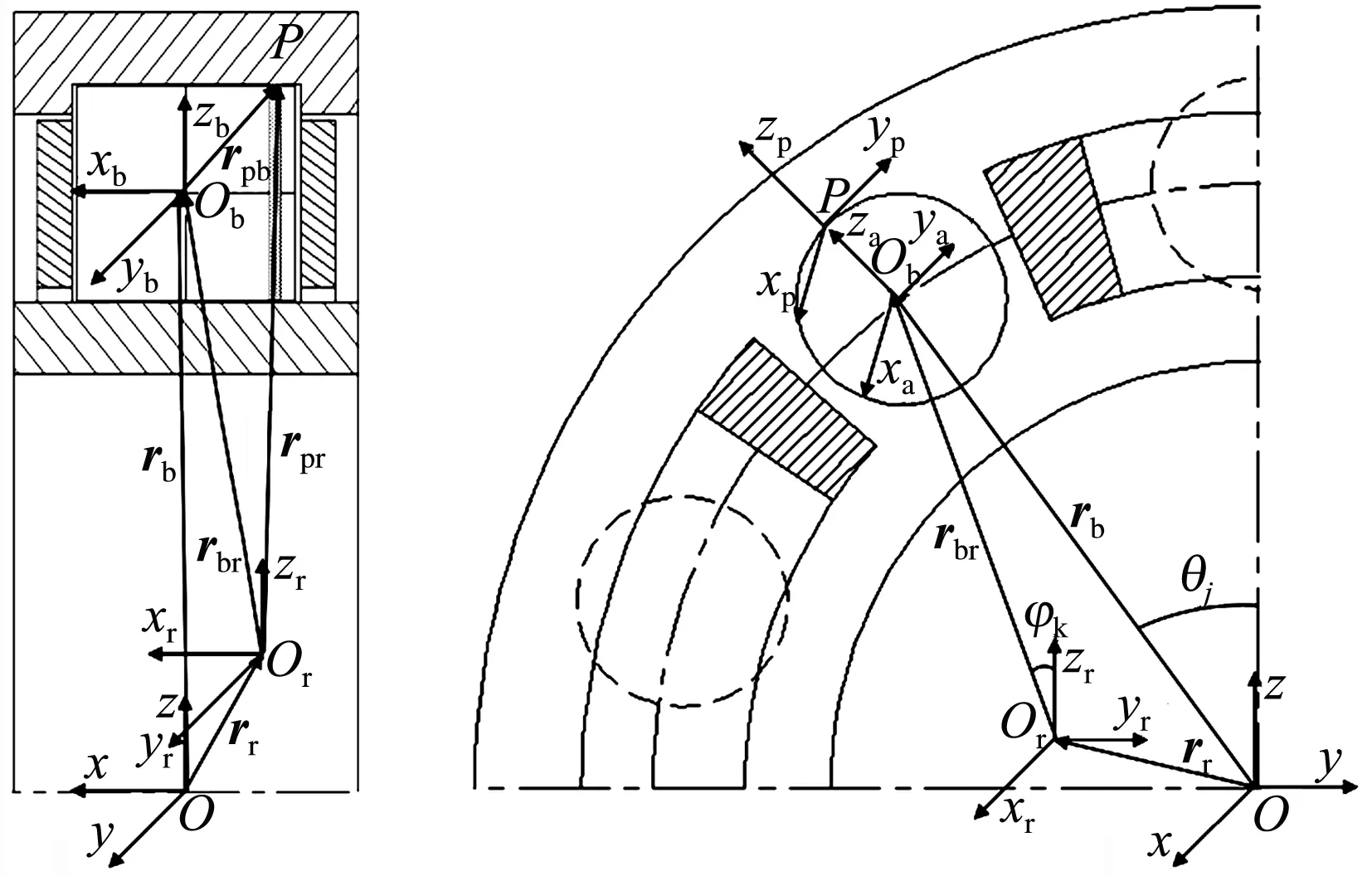
圖1 滾子與滾道幾何作用關(guān)系Fig.1 Geometric interactions between roller and raceway

rbr=Tir(rb-rr) ，

(1)

考慮滾子凸度結(jié)構(gòu)特點，對滾子進(jìn)行切片處理，切片與滾道的接觸點P到外圈中心的距離為

rpr=Trra(rbr+Tbrrpb) ，

(2)

則滾子與滾道之間的彈性接觸變形為

δ=rpr3-0.5dr，

(3)

式中：Tir為慣性坐標(biāo)系到外圈定體坐標(biāo)系的轉(zhuǎn)換矩陣；Trra為外圈定體坐標(biāo)系到外圈方位坐標(biāo)系的轉(zhuǎn)換矩陣；rpb為接觸點P到滾子中心的距離；dr為外滾道直徑；下標(biāo)3表示rpr的第3項。

根據(jù)赫茲公式和部件運動學(xué)關(guān)系，可計算得到滾子方位坐標(biāo)系下作用于滾子的合力Frb，滾子定體坐標(biāo)系下作用于滾子的力矩Mrb，慣性坐標(biāo)系下作用于外圈的合力Fbre，外圈定體坐標(biāo)系下作用于外圈的力矩Mbre，慣性坐標(biāo)系下作用于內(nèi)圈的合力Fbri，內(nèi)圈定體坐標(biāo)系下作用于內(nèi)圈的力矩Mbri，詳細(xì)計算過程可參考文獻(xiàn)[26]。

1.2 滾道局部故障模型

若軸承滾道表面出現(xiàn)局部故障，滾子通過故障區(qū)域時，滾道表面材料缺失，則受故障影響的接觸變形δr為

(4)

式中：δ為滾子與正常滾道的接觸變形；δd為滾子與故障滾道的接觸變形；φ0為故障區(qū)域初始位置角；φd為故障區(qū)域的弧長；φf為滾子方位角。

1.3 外圈與軸承座作用關(guān)系模型

如圖2所示，建立接觸坐標(biāo)系Ocxcyczc，Or為外圈中心，rr為位置向量，vr為速度向量；Oh為軸承座中心，初始與慣性坐標(biāo)原點重合，rh為位置向量，vh為速度向量。慣性坐標(biāo)系到接觸坐標(biāo)系的轉(zhuǎn)換矩陣為Tic(θ,0,0)，而θ可表示為

圖2 外圈與軸承座作用關(guān)系Fig.2 Interaction between outer ring and housing

(5)

式中：rrh2,rrh3分別為外圈相對軸承座中心向量rrh的第2，3項。

接觸坐標(biāo)系中，外圈與軸承座之間的接觸力pn和摩擦力pt分別為

(6)

式中：kr為外圈與軸承座間的接觸剛度；erh為外圈與軸承座間的間隙；μrh為外圈與軸承座間的摩擦因數(shù)；vrh2為接觸坐標(biāo)系中外圈相對軸承座的滑動速度向量vrh的第2項。

慣性坐標(biāo)系中作用于外圈的力Fhr為

Fhr=[0ptpn]T，

(7)

作用于外圈的力矩Mhr為

Mhr=rrc×(TirFhr)，

(8)

作用于軸承座的力Frh為

Frh=-Fhr，

(9)

式中：rrc為外圈定體坐標(biāo)系下外圈與軸承座的接觸點到外圈中心的位置向量；Tir為慣性坐標(biāo)系到外圈定體坐標(biāo)系的轉(zhuǎn)換矩陣。

1.4 軸承系統(tǒng)動力學(xué)方程

基于上述計算獲得作用力和力矩，以牛頓-歐拉方程構(gòu)建考慮軸承外圈與軸承座間隙的滾道故障圓柱滾子軸承系統(tǒng)運動控制方程[26]。

滾子方位坐標(biāo)系中，滾子移動控制方程為

(10)

式中：mb為滾子質(zhì)量；rj為第j個滾子徑向位置；g為重力加速度；Frb2,Frb3分別為滾子方位坐標(biāo)系下作用于滾子的力Frb的第2，3項；θj為滾子方位角。

慣性坐標(biāo)系中，內(nèi)圈移動控制方程為

(11)

式中：mi為內(nèi)圈總質(zhì)量；Fbri2,Fbri3分別為慣性坐標(biāo)系下作用于內(nèi)圈的力Fbri的第2，3項；yi,zi分別為慣性坐標(biāo)系下內(nèi)圈在y，z方向的位移；Fr為外界施加于軸承的徑向載荷。

慣性坐標(biāo)系中，外圈移動控制方程為

(12)

式中：me為外圈質(zhì)量；ye,ze分別為慣性坐標(biāo)系下外圈在y，z方向的位移；Fbre2,Fbre3分別為慣性坐標(biāo)系下作用于外圈的力Fbre的第2，3項；Fhr2,Fhr3分別為慣性坐標(biāo)系下作用于外圈的力Fhr的第2，3項。

部件(滾子和外圈)固定坐標(biāo)系中，各部件的旋轉(zhuǎn)控制方程為

I1w1-(I2-I3)w2w3=M1，

(13)

式中：I1,I2,I3為部件(滾子和外圈)的轉(zhuǎn)動慣量；w1,w2,w3為部件(滾子和外圈)的角速度向量；M1為部件作用力矩(Mrb，Nbre+Mhr)的第1項。

慣性坐標(biāo)系中，軸承座移動控制方程為

(14)

式中：mh為軸承座質(zhì)量；khy,khz分別為軸承座在y，z方向的剛度；chy,chz分別為軸承座在y，z方向的阻尼；Frh2，F(xiàn)rh3分別為慣性坐標(biāo)系下作用于外圈的力Frh的第2，3項。

2 滾道故障軸承振動分析

本文所分析圓柱滾子軸承的結(jié)構(gòu)參數(shù)及工況參數(shù)見表1，以擬靜力學(xué)計算結(jié)果為初值，采用變步長龍格-庫塔方法求解系統(tǒng)控制方程，獲得軸承零件的動力學(xué)參數(shù)[27]。

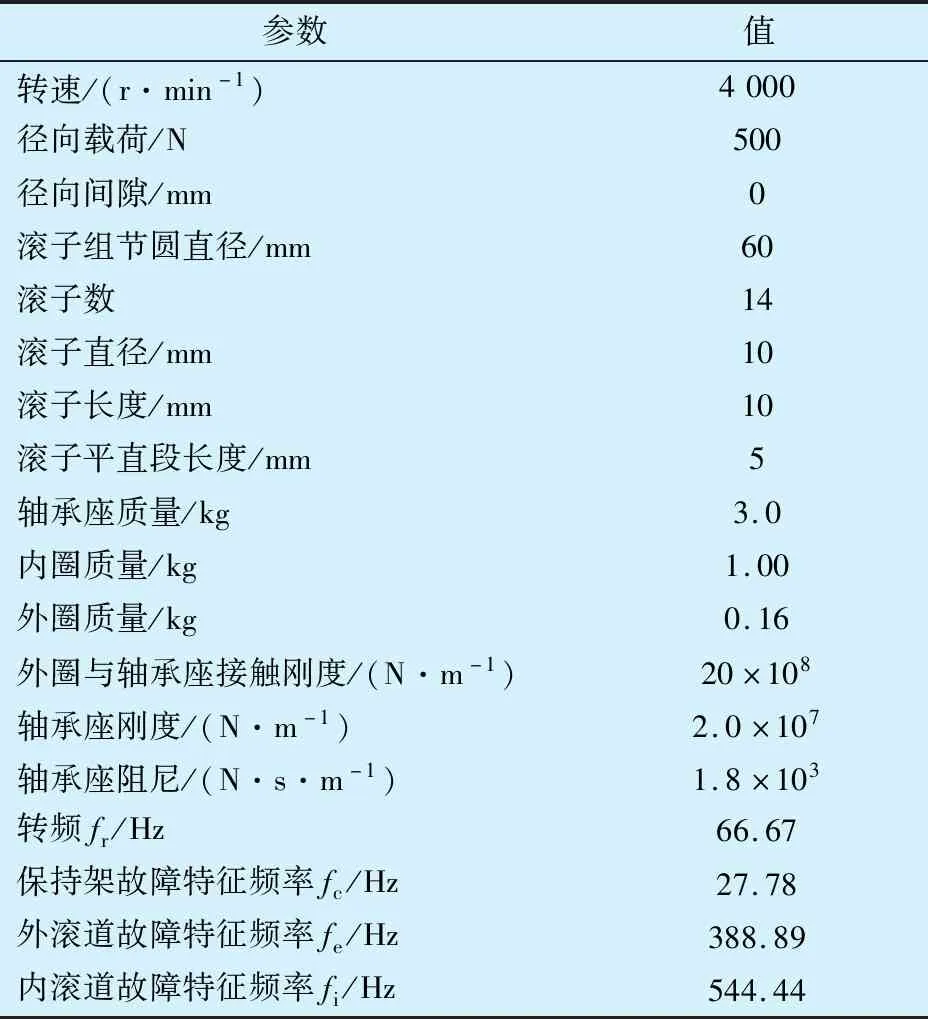
表1 圓柱滾子軸承結(jié)構(gòu)及工況參數(shù)Tab.1 Structure and working condition parameters of cylindrical roller bearing

2.1 間隙對外滾道故障軸承振動的影響

當(dāng)外圈與軸承座之間出現(xiàn)間隙時，受作用力影響，外圈相對軸承座轉(zhuǎn)動，接觸界面發(fā)生相對滑動，產(chǎn)生摩擦力，其大小受摩擦因數(shù)μrh影響[28]。當(dāng)外圈與軸承座間的摩擦因數(shù)為0.3時，間隙對外滾道故障軸承振動信號的影響如圖3所示：不同間隙下，軸承座z方向加速度出現(xiàn)周期性沖擊，未發(fā)現(xiàn)顯著區(qū)別，整體變化規(guī)律一致，且相鄰沖擊峰間的時間間隔與外滾道故障特征頻率fe相對應(yīng)；沖擊峰局部放大時，沖擊峰出現(xiàn)時間隨間隙增大而提前，但最大峰峰值減小。

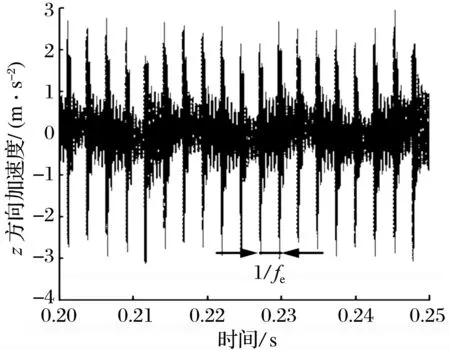
圖3 不同間隙下外滾道故障軸承的振動響應(yīng)Fig.3 Vibration response of bearing with outer raceway fault under different clearances

間隙對外滾道故障軸承振動信號包絡(luò)譜的影響如圖4所示：外滾道故障特征頻率突出且在不同間隙下保持一致；存在保持架故障特征頻率fc及其倍頻，對外滾道故障特征頻率fe有一定調(diào)制作用(如fe+fc，fe-fc)；外滾道故障頻率fe的幅值最大，其他倍頻的幅值依次減小，放大外滾道故障特征頻率附近區(qū)域可知，間隙為0時幅值最小，25 μm時幅值最大，原因在于外圈與軸承座之間的作用力隨間隙增大而改變，直接影響作用于軸承座的豎直方向分力，改變時域信號的沖擊峰峰值，以致出現(xiàn)圖4b中的頻域特征。

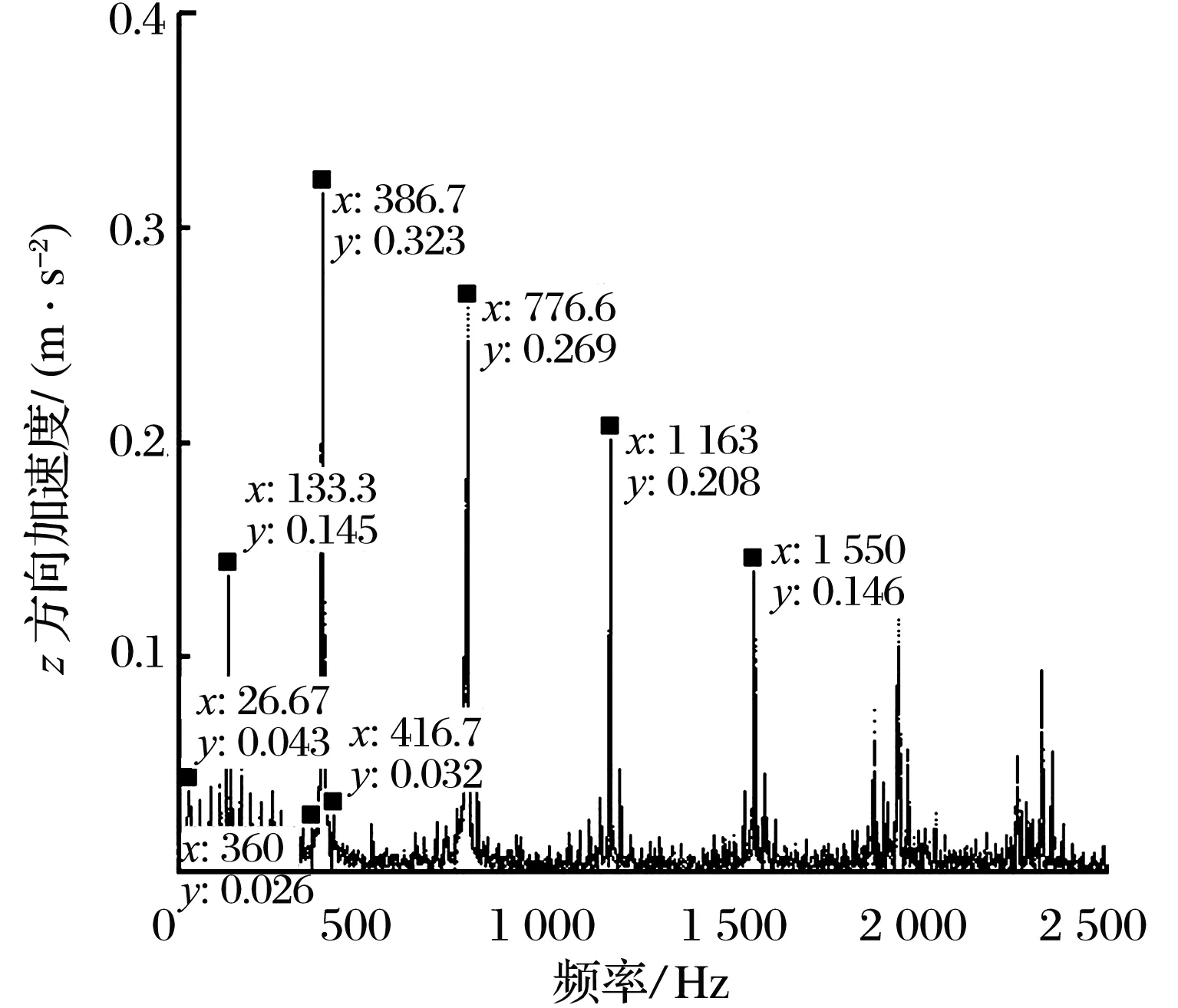
圖4 不同間隙下外滾道故障軸承振動信號的包絡(luò)譜Fig.4 Envelope spectrum of vibration signal of bearing with outer raceway fault under different clearances

當(dāng)外圈與軸承座間隙為50 μm時，摩擦因數(shù)對外滾道故障軸承振動信號的影響如圖5所示：與間隙的影響相似，不同摩擦因數(shù)下軸承座z方向加速度同樣出現(xiàn)周期性沖擊，相鄰沖擊峰間的時間間隔與外滾道故障特征頻率fe相對應(yīng)；沖擊峰局部放大時(第0.275 8 s)，局部出現(xiàn)高頻波動，波動幅值隨摩擦因數(shù)的增大而增大。

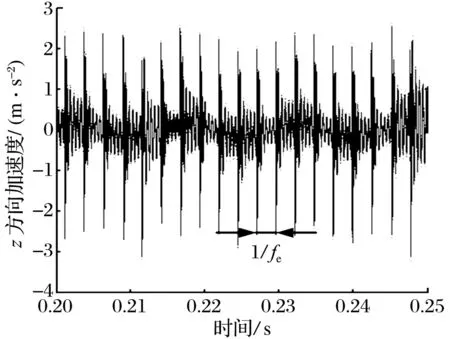
圖5 不同摩擦因數(shù)下外滾道故障軸承的振動響應(yīng)Fig.5 Vibration response of bearing with outer raceway fault under different friction coefficients

摩擦因數(shù)對外滾道故障軸承振動信號包絡(luò)譜的影響如圖6所示：與間隙影響一致，存在保持架故障特征頻率fc及其倍頻，外滾道故障特征頻率fe及其倍頻(如2fe，3fe)和間隔為保持架故障特征的邊頻帶(如fe+fc，fe-fc)；放大外滾道故障特征頻率附近區(qū)域的放大結(jié)果表明，幅值隨摩擦因數(shù)的增大而減小。

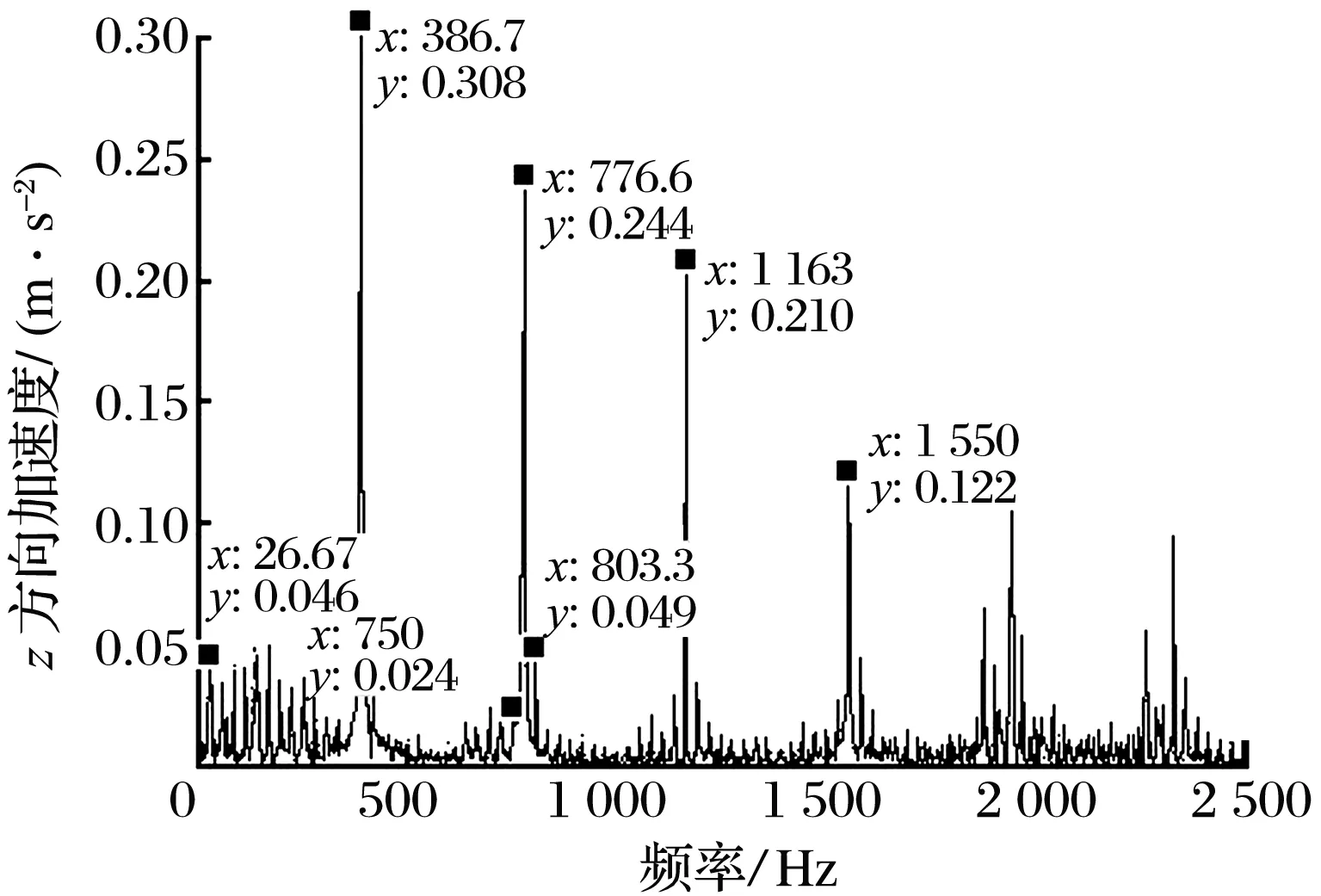
圖6 不同摩擦因數(shù)下外滾道故障軸承振動信號的包絡(luò)譜Fig.6 Envelope spectrum of vibration signal of bearing with outer raceway fault under different friction coefficients

2.2 間隙對內(nèi)滾道故障軸承振動的影響

當(dāng)外圈與軸承座間的摩擦因數(shù)為0.3時，間隙對內(nèi)滾道故障軸承振動信號的影響如圖7所示：不同間隙下，軸承座z方向加速度規(guī)律一致，短時間內(nèi)出現(xiàn)連續(xù)沖擊，形成沖擊集中區(qū)，單沖擊集中區(qū)內(nèi)相鄰沖擊峰間的時間間隔與內(nèi)滾道故障特征頻率fi相對應(yīng)，而相鄰沖擊集中區(qū)同等位置沖擊峰之間的時間間隔則與轉(zhuǎn)頻fr相對應(yīng)；對最大沖擊峰附近區(qū)域放大可知，沖擊峰出現(xiàn)的時間隨間隙增大而滯后，但最大峰的峰值一致。

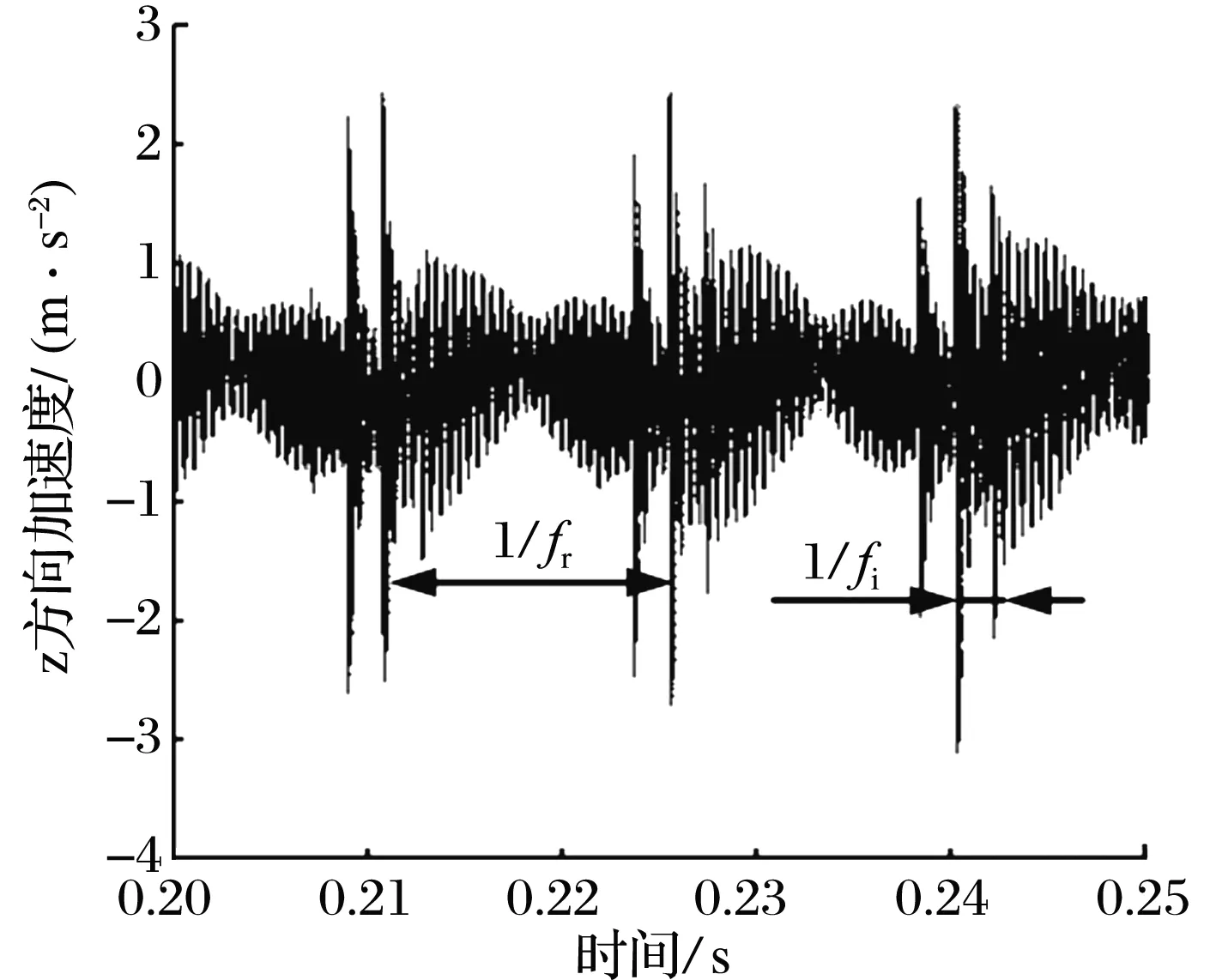
圖7 不同間隙下內(nèi)滾道故障軸承的振動響應(yīng)Fig.7 Vibration response of bearing with inner raceway fault under different clearances

間隙對內(nèi)滾道故障軸承振動信號包絡(luò)譜的影響如圖8所示：不同間隙下，內(nèi)滾道故障特征頻率一致，同時存在轉(zhuǎn)頻fr及其倍頻、內(nèi)滾道故障特征頻率fi及其倍頻附近有間隔為轉(zhuǎn)頻的邊頻帶(fi+fr，fi-fr，2fi-fr，2fi+fr)；對內(nèi)滾道故障特征頻率附近區(qū)域放大可知，0，25，50 μm間隙時幅值依次增大，而75 μm間隙時的幅值急劇減小。

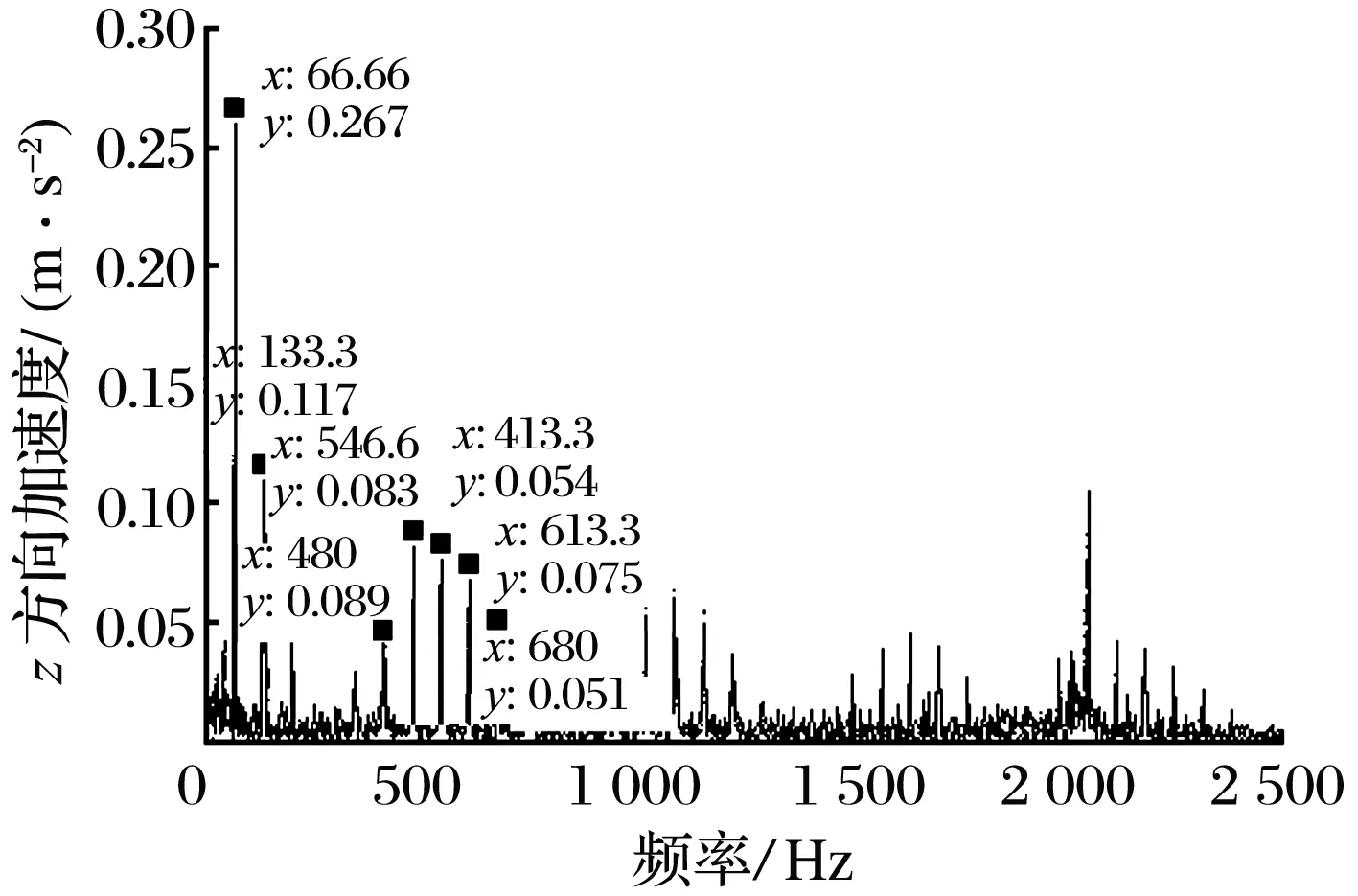
圖8 不同間隙下內(nèi)滾道故障軸承振動信號的包絡(luò)譜Fig.8 Envelope spectrum of vibration signal of bearing with inner raceway fault under different clearances

當(dāng)外圈與軸承座間隙為50 μm時，摩擦因數(shù)對內(nèi)滾道故障軸承振動信號的影響如圖9所示：與間隙影響相似，不同摩擦因數(shù)下內(nèi)滾道故障軸承振動信號中存在一致的周期性沖擊；最大沖擊峰局部放大時也存在高頻波動，波動幅值隨摩擦因數(shù)的增大而增大。

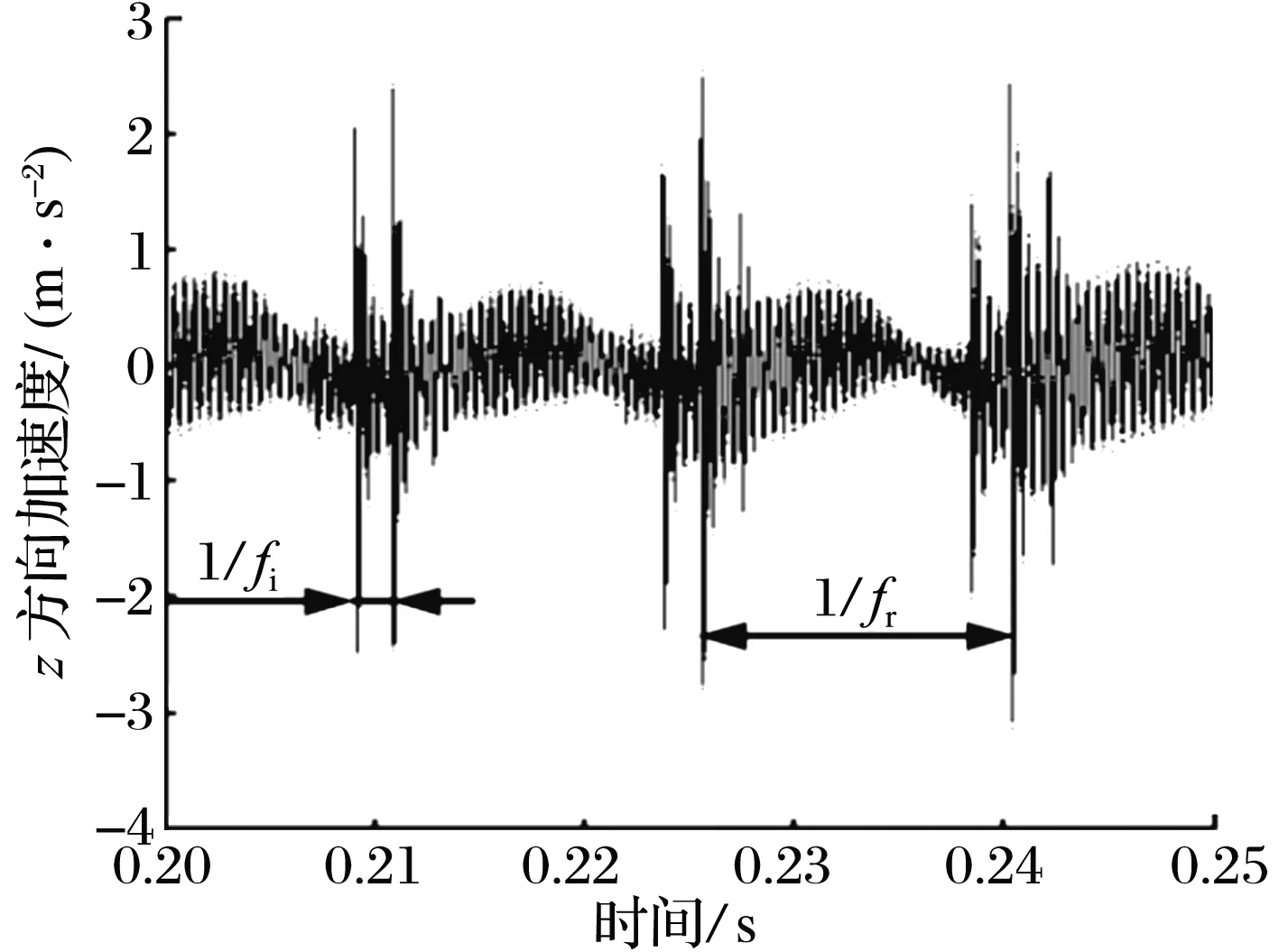
圖9 不同摩擦因數(shù)下內(nèi)滾道故障軸承的振動響應(yīng)Fig.9 Vibration response of bearing with inner raceway fault under different friction coefficients

摩擦因數(shù)對內(nèi)滾道故障軸承振動信號包絡(luò)譜的影響如圖10所示：與間隙影響相似，出現(xiàn)了相同故障頻率特征；對內(nèi)滾道故障特征頻率附近區(qū)域放大可知，摩擦因數(shù)0.3時幅值最大，0.7時幅值最小。摩擦因數(shù)增大，外圈與軸承座之間的摩擦力增大，影響作用于軸承座的豎直方向分力，改變時域信號沖擊峰峰值，使特征頻率幅值減小。

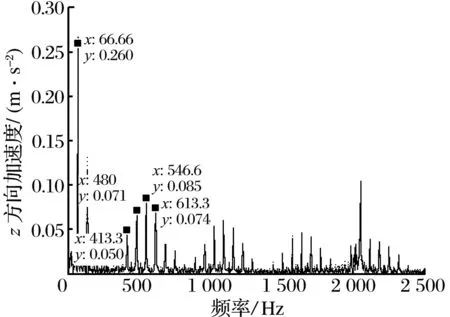
圖10 不同摩擦因數(shù)下內(nèi)滾道故障軸承振動信號的包絡(luò)譜

2.3 有無間隙對滾道故障軸承振動的影響

為體現(xiàn)本文所建外圈與軸承座間隙模型的特點，將文獻(xiàn)[29]中外圈與軸承座一體化的振動分析結(jié)果與本文中間隙為0的結(jié)果進(jìn)行對比。鑒于滾道故障產(chǎn)生的振動響應(yīng)是周期性的，取一個周期的振動信號進(jìn)行分析，結(jié)果如圖11所示： 相對于外圈與軸承座一體化模型，考慮外圈與軸承座間隙時的模型能描述外圈與軸承座的作用關(guān)系，更接近實際情況，且滾道故障軸承的振動幅值小很多，振動信號更加豐富，更能反應(yīng)實際軸承復(fù)雜振動信號的來源。

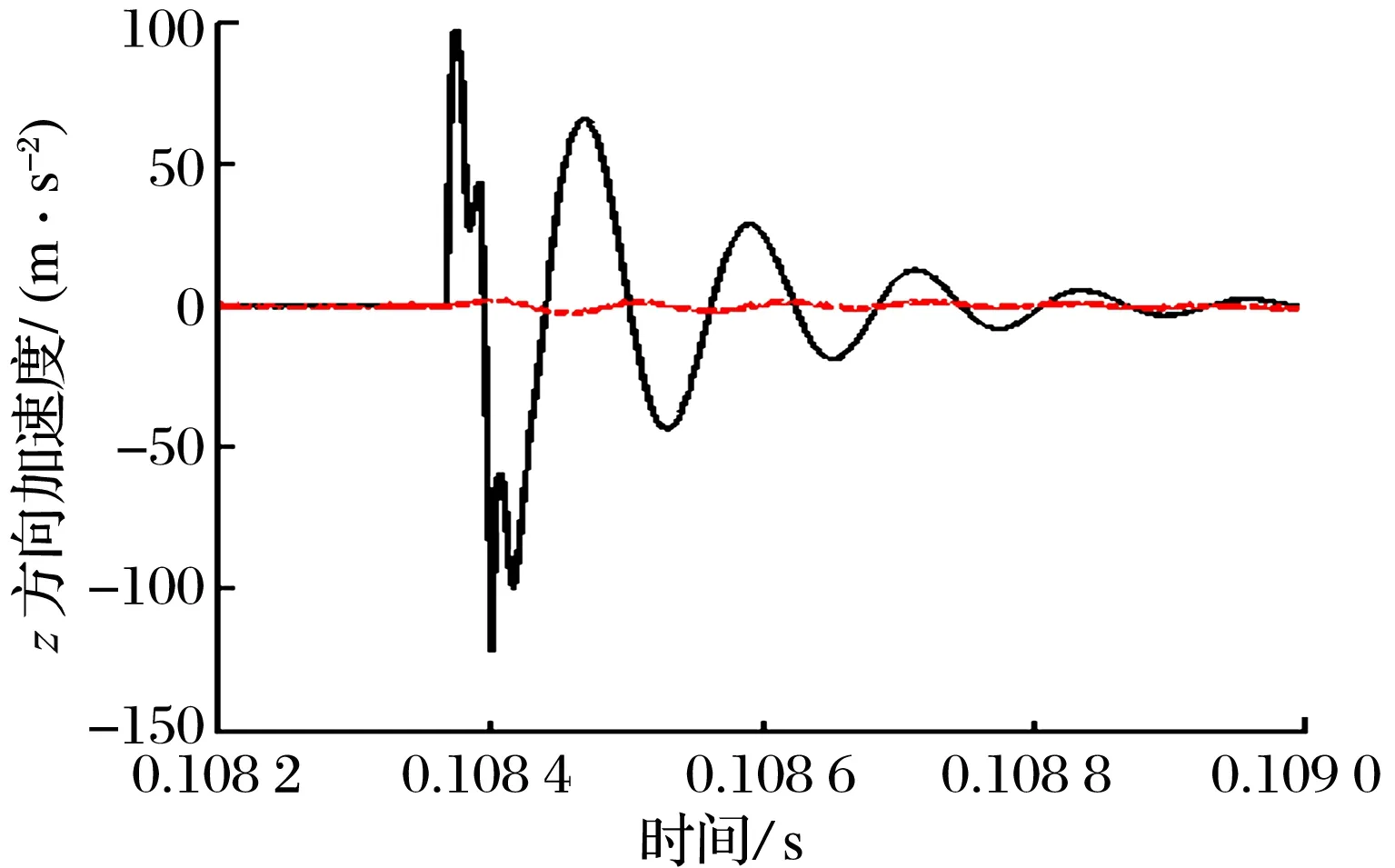
(a)外滾道故障

3 試驗驗證

為驗證本文所建立圓柱滾子軸承故障動力學(xué)模型的可靠性，搭建如圖12所示的故障軸承試驗平臺，試驗軸承如圖13所示，滾子組節(jié)圓直徑60 mm，軸承寬度18 mm，滾子直徑10 mm，滾子個數(shù)12，故障寬度0.2 mm、深度0.2 mm，外圈與軸承座間隙為0。軸承轉(zhuǎn)頻fr為16.67 Hz，保持架故障特征頻率fc為7.53 Hz，外滾道故障特征頻率fe為188.33 Hz，內(nèi)滾道故障特征頻率fi為228.33 Hz。

圖12 故障軸承測試試驗臺Fig.12 Test rig for faulty bearing

(a)內(nèi)滾道故障

依據(jù)文獻(xiàn)[24]的試驗過程進(jìn)行試驗，試驗結(jié)果與理論分析結(jié)果的對比如圖14所示：

1)外滾道故障時，存在保持架故障特征頻率fc，外滾道故障特征頻率fe及其2倍頻，以及以保持架故障特征頻率為間隔的邊頻帶(fe-fc，fe+fc)，外滾道故障特征頻率幅值最大，保持架故障特征頻率幅值最小，試驗結(jié)果與理論分析結(jié)果相應(yīng)頻率的最大誤差為1.44%。

2)內(nèi)滾道故障時，存在轉(zhuǎn)頻fr及其二倍頻，內(nèi)滾道故障特征頻率fi及其二倍頻，以及以轉(zhuǎn)頻為間隔的邊頻帶(fi-fr，fi+fr，2fi-fr，2fi+fr)，轉(zhuǎn)頻幅值大于內(nèi)滾道故障特征頻率幅值，內(nèi)滾道故障特征頻率2倍頻幅值最小，試驗結(jié)果與理論分析結(jié)果相應(yīng)頻率的最大誤差為2.52%。

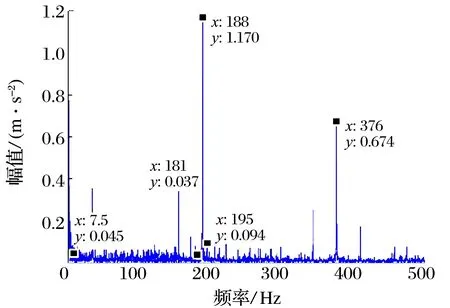
(a)外滾道故障試驗結(jié)果

4 結(jié)論

通過接觸變形引入故障激勵，分析外圈與軸承座作用關(guān)系，獲取軸承零件承受的作用力和力矩，借助牛頓-歐拉方程建立考慮外圈與軸承座間隙影響的滾道故障圓柱滾子軸承動力學(xué)分析模型，通過理論分析和試驗得到以下結(jié)論：

1)外滾道存在局部故障時，軸承座豎直方向時域振動信號出現(xiàn)周期性沖擊和對應(yīng)的故障特征頻率，沖擊峰出現(xiàn)時間隨外圈與軸承座間隙增大而提前，但峰峰值減小；間隙為0時故障特征頻率幅值最小，25 μm時故障特征頻率幅值最大；時域振動信號局部高頻波動幅值隨摩擦因數(shù)增大而增大，故障特征頻率幅值則隨之減小。

2)內(nèi)滾道存在局部故障時，軸承座豎直方向時域振動信號短時間出現(xiàn)多次沖擊，時間間隔與轉(zhuǎn)頻和故障特征頻率相對應(yīng)，沖擊峰出現(xiàn)時間隨外圈與軸承座間隙增大而滯后，峰峰值無區(qū)別；在間隙0，25，50 μm時，內(nèi)滾道故障特征頻率幅值隨間隙增大而增大，而間隙75 μm時幅值則急劇減小；時域振動信號局部高頻波動幅值隨摩擦因數(shù)增大而增大，摩擦因數(shù)0.3時內(nèi)滾道故障特征頻率的幅值最大，0.7時最小。