臨近空間高超聲速飛行器的直接力與襟翼復合滑模控制

董金魯， 馬悅萌， 周荻， 龔曉剛， 張曦， 宋加洪

(1.山東交通學院 信息科學與電氣工程學院(人工智能學院)， 山東 濟南 250000；2.哈爾濱工業大學 航天學院， 黑龍江 哈爾濱 150001； 3.北京航天長征飛行器研究所， 北京 100076)

0 引言

臨近空間高超聲速再入飛行器具有遠距離攻擊、強機動突防、精確打擊和攻擊威力大等突出優點，使得此類飛行器受到越來越多的重視，同時也對國家安全防御系統帶來新的挑戰[1-2]。高超聲速飛行器可以在臨近空間長時間巡航飛行，其工作具有長航時、廣空域及頻繁機動等特點。高超聲速飛行器在再入過程中將遭受惡劣的氣動熱環境與巨大的氣動扭矩，使得傳統的舵面很可能在再入過程中燒蝕變形。為解決這一問題，襟翼由于其在減少氣動熱燒蝕方面的顯著優勢[3]，成為再入式高超聲速飛行器氣動控制的一個優先選擇[4]。目前襟翼控制已發展到實用化階段，國外已有許多成功案例，如美國雙錐削面升力體構形的高超聲速飛行器HTV-1和類乘波構形的HTV-2[5]、歐洲太空局試飛成功的過渡性實驗飛行器(IXV)以及最近俄羅斯公布的“先鋒”高超聲速飛行器。

升力體構型的高超聲速飛行器在飛行器的速度從幾馬赫變化到20馬赫以上情況下可實現更寬的再入走廊，但較大的飛行包線會導致空氣動力系數劇烈變化[6]；高超聲速飛行器細長的幾何外形和輕型結構使彈體易產生彈性變形，從而對剛體動力學造成嚴重干擾[7]；飛行器在臨近空間機動飛行時，由于飛行高度較高、氣動壓低，氣動舵很難滿足控制命令的需求。為此，通常引入直接力作為輔助執行機構，為飛行器提供快速響應。為使氣動舵與直接力更好地配合，達到即節省能量又提高系統動態特性的目的，通常對兩種執行機構進行邏輯分配[8-10]。文獻[8]指出對于復合控制輸入混合問題，常采用菊花鏈法和偽逆法，但這兩種方法都存在缺點，菊花鏈法在穩態時直接力不輸出，但在瞬時作用時非常大，常會造成輸入的突變，不利于平滑控制。偽逆法在穩態時反作用力也不為零，造成能量的浪費。文獻[9]考慮氣動舵飽和輸入的限制，針對控制命令，優先分配給氣動舵，若氣動舵飽和，則通過控制分配算法分配給側噴發動機以輔助氣動舵完成控制命令；為使側噴發動機更好地配合氣動舵，文中縱向通道提出一種自適應地生成氣動舵與反作用控制系統(RCS)的控制命令，同時考慮攻角約束和不確定參數[10]。復合控制也常與有限時間控制理論相結合[9，11-12]，文獻[9]中設計終端滑模控制器以提高系統的魯棒性，并通過神經學習和擾動觀測器保證系統的有限時間收斂。將固定時間收斂與滑模技術相結合，可確保系統在不同的初始條件下在有界時間內收斂，與文獻[9]提到的終端滑模不同的是，其穩定的時間界限與初始狀態無關[11]。文獻[12]針對氣動舵控制回路基于有限時間穩定理論得到一個高性能受控彈體，并針對新的受控彈體基于Backstepping技術設計關于直接力的控制律。Liu等[13]考慮側噴發動機射流相互的影響，提出一種改進的模型預測控制方法，與經典控制方法作仿真對比，證明了所提方案的有效性和效率。側噴發動機的開關性與襟翼的連續性使得復合系統成為一個混合控制系統[14]，這些問題使得臨近空間高超聲速飛行器的直接力與襟翼復合控制器設計極富挑戰[15]。

當機身以大攻角飛行時，機身阻擋了舵附件的氣流，方向舵效率大幅度下降，高超聲速簡化為僅有兩個控制舵的欠驅動系統[16]。此外，當舵損壞時及縱向舵間的耦合，都會使得飛行器變為欠驅動系統[17]。欠驅動機構也有許多優點：減小舵的質量、降低成本及能量消耗、重新設計飛行器的配置[18]。

文獻[19]針對欠驅動飛行器設計了自適應控制系統，通過移動質量塊和側噴發動機達到控制飛行器姿態動力學的目的，并基于不變性理論設計了氣動參數的估計器，用于對不確定項的補償。文獻[20]基于觀測器對存在洋流的欠驅動船舶提出了跟蹤曲線路徑問題的解決方案。文獻[21]從理論層面和數值仿真方面都證明了飛行器在僅有襟翼控制的條件下，控制器可以穩定控制飛行器。

HTV-2A試驗失敗的原因之一是飛行器偏航運動超出預期上界[22]。由于滾轉通道與偏航通道間的強耦合作用，滾轉角速率隨著側滑角的增大而不斷增大，最終導致副翼控制量飽和，飛行器失穩。因此為提高偏航的控制力度以確保飛行安全，本文將一對側噴發動機作為輔助執行機構引入飛行器的偏航通道(見圖1，其中O、E分別為飛行器質心、飛行器后視圖截面的中心，OXbYbZb為飛行器的體坐標系，Flap為飛行器的襟翼執行機構)，這時高超聲速飛行器的姿態控制是由側噴發動機與兩個體襟翼(提供等效升降舵和副翼控制量)聯合實現的。

圖1 復合控制高超聲速飛行器框架結構圖Fig.1 Schematic diagram of a hypersonic vehicle with the composite control scheme

在過去幾十年中，反饋線性化方法[23]、切換控制[24]、模糊控制[25]、神經網絡控制[26]和反步控制[27]等控制方法被廣泛應用于高超聲速飛行器自動駕駛儀的設計中。然而，這些設計均沒有考慮襟翼與側噴發動機的復合控制以及側噴發動機的開關動作特點。本文將充分考慮襟翼的連續工作特性和側噴發動機的開關工作特性，并選擇合適的控制方法設計襟翼與側噴發動機的控制律。

本文針對臨近空間飛行器氣動力不足以及傳統氣動舵面在高超聲速再入過程中燒蝕嚴重等問題，將襟翼與側噴發動機相結合，對再入式高超聲速飛行器進行復合控制。側噴發動機的引入使側滑角能夠被限制在小范圍內波動，對該非線性控制系統進行解耦與線性化，得到俯仰與滾轉- 偏航兩個子系統，進一步應用線性最優二次型控制方法，分別對兩個子系統設計等效升降舵與副翼控制律。

將設計好的襟翼控制律代入滾轉- 偏航通道子系統模型中，形成新的受控模型，以側噴發動機的輸出作為新受控對象的控制輸入。為與噴發動機的開關工作特性相匹配，運用滑模控制理論設計控制律是一種合理的選擇[28]。文獻[29]在考慮不確定和外部干擾的情況下，基于擾動觀測器，為高超聲速飛行器設計了自適應高階滑模控制器。但尚未有公開文獻將滑模控制理論應用于襟翼和側噴發動機的復合控制系統。滑模控制的主要缺點是滑動流形上的抖振現象，將引起系統的高頻特性，不利于制導控制的實現。為改善非線性控制系統的性能，本文提出一種帶邊界層的變結構滑模控制器來抑制系統中的抖振，從而消除抖振現象，進而減少燃料的消耗。

已有研究大多只是將單一執行機構(襟翼或側噴發動機)應用于飛行的某一階段，本文注重考慮飛行器從大氣層外再入到大氣層內這一過程，空氣密度低、飛行速度高、極端的氣動熱環境與低氣動力操縱性是這一階段的主要特點，因此引入襟翼+側噴發動機并在控制系統設計時充分考慮了氣動執行機構的連續特性與直接力執行機構的離散特性，建立復合控制系統，以實現飛行器在臨近空間再入段的高精度控制。

本文的主要創新點包括：

1)為解決常規舵再入過程中的燒蝕問題，巧妙引入具有良好熱防護性能的襟翼執行機構。

2)針對欠驅動強耦合高超聲速飛行器在臨近空間飛行時氣動力嚴重不足的問題，提出襟翼與側噴發動機的復合控制解決途徑，靈活地將襟翼與側噴發動機結合在一起，在臨近空間滑翔段各自發揮其獨特優勢，以提高再入飛行器的可操縱性。

3)根據實際情形，充分考慮側噴發動機Bang-Bang特性，首先通過非奇異變換將生成的復合控制模型轉換為標準型，然后應用滑模變結構控制理論設計滑模控制器，將具有連續和離散不同類型的執行機構較好地進行結合。

4)為同時達到節省側噴發動機燃料和消除滑模面抖振現象的目的，對滑模面引入邊界層進行改善。

1 直接側向力與襟翼復合控制數學模型

帶有襟翼與直接側向力的復合控制系統高超聲速飛行器如圖1所示，襟翼作為控制系統的執行機構，只能提供等效的升降舵控制量δz與副翼控制量δx，系統中缺乏方向舵控制量δy。由于偏航通道與滾轉通道間存在一定的氣動耦合[30]，可以在偏航通道中引入副翼控制量δx，即使用副翼控制量δx同時控制偏航、滾轉兩個通道。同時為避免側滑角發散，在滾轉通道中引入了側滑角反饋量。

由于氣動耦合對偏航通道的控制效果較弱，尤其是在動壓不足的情況下，本文在偏航通道中引入一對側噴發動機，此時高超聲速飛行器的數學模型中將不僅包含氣動力與氣動力矩，還包含側噴發動機產生的推力及相應力矩[31]。當側滑角低于設定閾值時，側噴發動機不工作；當側滑角超過設定閾值時，側噴發動機啟動以抑制側滑角的發散。

假定飛行器質量恒定且為剛體，簡化的飛行器質心運動方程表示如下：

(1)

(2)

式中：m和v分別表示飛行器的質量和速度；α和β分別表示攻角和側滑角；ωx、ωy和ωz分別表示滾轉、偏航和俯仰角速率；Fy和Fz分別為沿飛行器體坐標系Yb軸和Zb軸方向的分力。

作用在飛行器上的力由氣動力、反作用推力和重力構成，即

(3)

式中：Ya和Za表示升力和側向力；Ty和Tz表示側噴發動機在飛行器體坐標系Yb軸和Zb軸方向的反作用力；Gy和Gz為重力在飛行器體坐標系Yb軸和Zb軸方向的分力。

忽略慣性積，飛行器的姿態動力學方程表示如下：

(4)

式中：Jx、Jy和Jz分別為轉動慣量在飛行器體坐標系Xb、Yb和Zb三軸的分量；Mxa、Mya和Mza分別為氣動力對質心的力矩在體坐標系各軸上的分量；Mxt、Myt和Mzt分別為側噴發動機產生的直接力對質心的力矩在體坐標系各軸上的分量。用氣動力導數近似表示氣動力和氣動力矩為

Ya=Yα(α)α+Yδz(α)δz

(5)

Za=Zββ

(6)

(7)

(8)

(9)

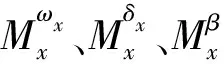
結合圖1，側噴發動機產生的直接力可表示如下：

Ty=0 N,Tz=FTz

(10)

式中：FTz表示兩個側噴發動機的推力之和。

由于側噴發動機的推力不通過質心，反作用力產生的力矩可表示為

Mxt=0 N·m,Myt=FTzl,Mzt=0

(11)

式中：l表示姿控發動機作用點到飛行器質心的距離。

將式(5)～式(11)代入式(1)、式(2)和式(4)，可得

(12)

(13)

(14)

(15)

(16)

滾轉通道動力學模型近似為

(17)

式中：γ為滾轉角。

至此，得到直接側向力與襟翼復合控制飛行器的6自由度數學模型，控制目標是在攻角與滾轉角快速跟蹤制導指令的同時將側滑角保持在0°附近。

2 高超聲速飛行器襟翼控制律的設計

2.1 縱向通道升降舵線性二次型最優控制律

由于側滑角始終約束在一定范圍內，β、ωy都是小值，俯仰通道模型可從非線性系統中解耦出來，利用線性二次型最優控制律設計控制量δz。俯仰通道的系統模型從式(12)～式(17)中解耦出來為

(18)

(19)

定義狀態變量和控制輸入分別為

(20)

式中：αc為攻角命令，積分項有助于消除攻角指令跟蹤的穩態誤差。則俯仰通道系統模型可寫成如下狀態空間形式為

(21)

式中：

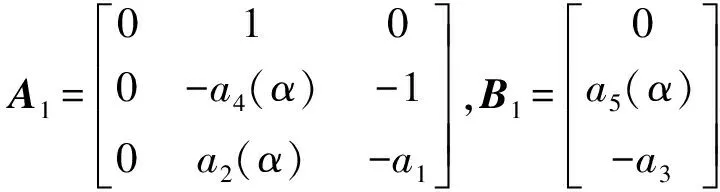
基于線性二次型最優控制理論[32]，針對系統式(21)設計出關于舵偏角的狀態反饋控制器：

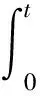
(22)

即

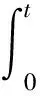
(23)

式中：Kp1、Kp2和Kp3分別為通過最小化式(24)的線性二次型性能指標而獲得的負反饋增益。

(24)

式中：Q1為半正定加權矩陣；R1為正常數。

2.2 橫側向通道副翼線性二次型最優控制律

偏航通道缺少直接的控制量，基于滾轉、偏航通道間的氣動耦合，利用δx對偏航通道進行控制，故將滾轉- 偏航通道聯合設計控制律。

由于升力體飛行器為面對稱結構，即Jy=Jz，有c4=0。側噴姿控發動機不工作時，側向通道系統模型可重寫為如下狀態空間形式：

(25)

式中：狀態變量X2=[γc-γωxβωy]T，γc為滾轉角命令；控制輸入u2=δx；狀態矩陣A2和輸入矩陣B2分別為

基于線性二次型最優控制理論，針對系統式(25)設計關于副翼偏角的狀態反饋控制器如下：

u2=KrX2=Kr1(γc-γ)+Kr2ωx+Kr3β+Kr4ωy

(26)

即

δx=Kr1(γc-γ)+Kr2ωx+Kr3β+Kr4ωy

(27)

式中：Kr1、Kr2、Kr3和Kr4分別為通過最小化式(28)的線性二次型性能指標而獲得的負反饋增益。

(28)

式中：Q2為半正定加權矩陣；R2為正常數。

3 高超聲速飛行器直接力的滑模控制律設計

3.1 橫側向通道直接側向力控制系統模型

在飛行過程中，當側滑角超過預設閾值時，側噴發動機開始工作，以抑制側滑角的發散。橫側向通道在側噴發動機工作時的系統模型為

(29)

側噴發動機工作過程中，氣動舵始終工作，因此將式(27)代入式(29)，可得新的狀態空間模型為

(30)

式中：狀態變量X3=[γc-γωxβωy]T；控制變量u3=FTz；狀態矩陣A3和輸入矩陣B3分別為

3.2 具有規范形式的線性系統滑模控制律設計方法

考慮到側噴發動機開關式的工作特點，選取滑模控制作為控制律的設計工具是一個很自然的選擇，此外滑模控制還可以處理系統中的模型不確定性與外部干擾，提高控制系統的魯棒性。

考慮一類線性系統

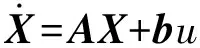
(31)

式中：X∈Rn為狀態變量，n為系統的維數；u∈R為控制輸入；(A,b)為規范形式，即控制變量b∈Rn的形式為b=[0 … 0bn]T，bn≠0，狀態矩陣A∈Rn×n的形式如下：

(32)

ri(i=0,1,…,n-1)為狀態矩陣的特征值。

對于此類線性系統，設計如下形式滑模面：

S(X)=p1x1+p2x2+…+pn-1xn-1+pnxn

(33)

式中：pi(i=1，2，…，n)滿足Hurwitz條件，且pn=1。

設計滑模控制律滿足如下形式：

(34)

式中：f1和f2分別為控制變量u的上界和下界。

假設系統的初始狀態X0是不屬于滑模面上的任意一點。為使點X0漸近收斂到滑模面上，必須滿足如下條件：

(35)

根據式(31)～式(35)可得

(36)

式中：p0=0。根據式(36)，可得如下滑模子空間：

(37)

顯然，滑模子空間的邊界由兩個平行的超平面給出，其表達形式如下：

(38)

定義p=[p1,p2,…,pn]T和r=[r0,r1,…,rn-1]T，則式(33)～式(38)可表示為如下緊集形式：

pTx=0

(39)

(rT-pTG)x=bnf1,2

(40)

式中：

為使滑模面屬于滑模子空間，可獲得如下方程：

(rT-pTG)=ρpT

(41)

式中：ρ∈R滿足下面等式

ρn-rn-1ρn-1+…+(-1)nr0=0

(42)

基于式(34)的控制輸入約束形式和由設計的滑模面決定的滑模子空間式(37)，針對式(31)描述的規范形式系統，如果滑模面系數滿足式(41)和Hurwitz條件，則所設計的滑模面屬于滑模子空間。

3.3 橫側向通道側噴發動機滑模控制律設計

(43)

線性非奇異變換矩陣為

(44)

式中：ri(i=1,2,3)為下式特征多項式的系數

det(sI-A3)=s4+r3s3+r2s2+r1s+r0

(45)

選取滑模面為

S(X)=p1x1+p2x2+p3x3+p4x4

(46)

式中：pi(i=1,2,3,4)滿足式(41)且滿足Hurwitz條件。則滑模控制律為

(47)

式中：Fs為單個側噴發動機的穩態推力。u3可確保所設計的滑模面屬于滑模子空間。

為消除抖振現象且節省燃料，對控制器增加邊界層設計如下：

(48)

式中：ε表示小的正值。

顯然，當S(X)>ε或S(X)<-ε時，滿足式(35)，即系統是完全可控的。

圖1中的飛行器姿控系統可以輸出不同量值的反作用力和反作用力矩。按照上述滑模控制律，可以根據當前的飛行狀態和指令要求，選取當前系統適合的控制力幅值。

4 直接力與襟翼復合控制系統仿真分析

表1 俯仰通道氣動參數Table 1 Aerodynamic parameters in the pitch channel

表2 偏航通道氣動參數Table 2 Parameters in the roll and yaw channels

表3 滾轉通道氣動參數Table 3 Parameters in the roll and yaw channels

為展示側噴姿控發動機的必要性，仿真中針對相同仿真條件下，對有無姿控發動機的控制進行比較分析。

4.1 情形1：跟蹤階躍信號

為驗證本文所設計控制律的快速精確性，攻角指令與滾轉角指令選為αc=10°和γc=90°的階躍信號，同時期望側滑角穩定在零度附近，即βc=0°。

為最小化性能指標式(24)及式(28)，增益矩陣Kp設計為Kp1=-20，Kp2=-15，Kp3=1.76；增益矩陣Kr設計為Kr1=-1.1，Kr2=0.97，Kr3=3.9，Kr4=0.55。

在設計姿控發動機的滑模控制律時，設計式(45)的特征多項式系數分別為r0=2 215.4，r1=1 974.4，r2=317，r3=6.90。

通過求解式(44)，可得線性非奇異變換矩陣為

根據式(41)和式(42)，漸近穩定的滑模面設計為

S(x)=445.4x1+307.4x2+1.93x3+x4

滑模控制律的邊界層設定為ε=1，單個姿控發動機的穩態推力為Fs=1 500 N。

在襟翼和側噴發動機的復合控制下，階躍函數的跟蹤響應曲線見圖2～圖7中的藍色實線，作為對比，圖2～圖7中的紅色虛線表示僅襟翼控制的階躍函數跟蹤響應曲線，綠色點線為階躍指令值。由圖2～圖4可知，在姿控發動機存在的情況下，攻角α1和滾轉角γ1完美跟蹤制導指令，同時側滑角快速的收斂到0°附近。從圖2中可見，攻角α1響應曲線的上升時間為0.18 s，最大超調量小于3%，由于側滑角β1的耦合效應，攻角α1在響應的初始階段存在一些不良振蕩。從圖3的側滑角響應曲線發現，由同一耦合效應導致的相似不良振蕩，隨著側滑角β1的快速收斂，攻角α1和滾轉角γ1逐漸變的平滑。

圖2 攻角響應曲線(情形1)Fig.2 Response curve of the angle of attack (Case 1)

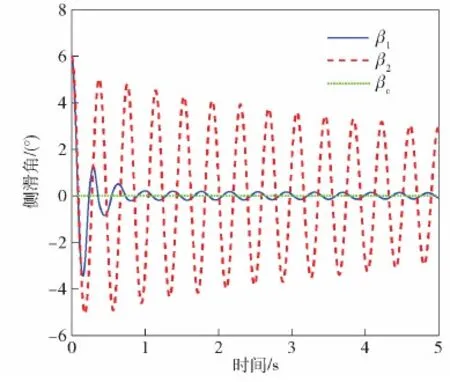
圖3 側滑角響應曲線(情形1)Fig.3 Response curve of the sideslip angle (Case 1)

圖4 滾轉角響應曲線(情形1)Fig.4 Response curve of the roll angle (Case 1)

作為對比，僅在襟翼控制下，側滑角β2的振蕩幅值比β1大的多，且其收斂速度也比β1慢(見圖3)。此外，β2的強振蕩被耦合到滾轉通道從而引發滾轉角響應的振蕩，在圖4中，滾轉角γ1以零過沖平滑的跟蹤命令信號，而滾轉角γ2以14%最大超調量在命令信號附近振蕩。僅襟翼控制下，β2的強振蕩耦合到俯仰通道造成攻角α2的超調量大于攻角α1的超調量，并且攻角α2的調節時間長于攻角α1。

控制變量δx和δz的響應曲線如圖5和圖6所示。圖5中，δx1表示復合控制，δx2表示僅襟翼控制。由于制導指令的階躍變化及不充分的氣動壓，控制量δx1和δx2在響應的初始階段均存在飽和現象。僅襟翼控制下，由于側滑角β2和滾轉角γ2的振蕩，δx2長時間處于飽和狀態；在復合控制下，δx1能夠很快地退出飽和狀態。圖6中，δz1表示復合控制下升降舵偏角的響應曲線，δz2表示僅襟翼控制下升降舵偏角的響應曲線。由圖6可以看出二者在響應初始階段都略微飽和，但均逐漸收斂，很快退出了飽和狀態，δz1最后收斂到一個常值，而δz2最后收斂到一個微小的振蕩狀態。姿控發動機響應曲線如圖7所示，側噴發動機只在動態過程(初始階段)中工作，穩態時一直處于關機狀態，避免了過多的燃料消耗和擾動。

圖5 副翼響應曲線(情形1)Fig.5 Response curve of the aileron (Case 1)

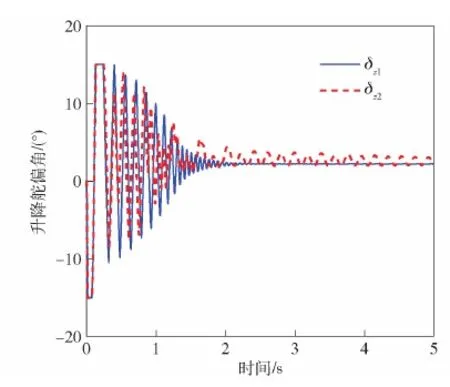
圖6 升降舵響應曲線(情形1)Fig.6 Response curve of the elevator (Case 1)

圖7 直接側向力響應曲線(情形1)Fig.7 Response curve of lateral jets (Case 1)

4.2 情形2：跟蹤正弦信號

飛行器的初始條件和情形1相同，期望高超聲飛行器執行正弦機動，即αc=10°sin (πt/4)，γc=45°sin (πt/4)，βc=0。

為最小化性能指標式(24)及式(28)，增益矩陣Kp設計為Kp1=-23，Kp2=-15，Kp3=1.76；增益矩陣Kr設計為Kr1=-1.1，Kr2=0.87，Kr3=3.9，Kr4=0.55。

通過求解式(44)，可得線性非奇異變換矩陣為

根據式(41)和式(42)，漸近穩定的滑模面設計為

S(x)=565.4x1+308.2x2+2.21x3+x4

滑模控制律的邊界層設定為ε=1，單個姿控發動機的穩態推力為Fs=1 500 N。

在襟翼和側噴發動機的復合控制下，正弦變化的攻角和滾轉角的跟蹤曲線見圖8～圖9中的藍色實線。作為對比，圖8～圖9中的紅色虛線表示僅襟翼控制的攻角和滾轉角的跟蹤響應曲線。由圖8～圖10可知，姿控發動機存在的情況下攻角α1和滾轉角γ1快速平滑地跟蹤上正弦指令，同時側滑角β1快速收斂到0°附近。僅襟翼控制下，側滑角β2的振蕩幅值比側滑角β1大得多，且在給定仿真時間內難以收斂。側滑角β2的振蕩耦合到滾轉通道導致滾轉角γ2發生相應的振蕩，如圖9所示。僅襟翼控制下，側滑角的大振蕩被耦合到俯仰通道中使得攻角指令的跟蹤產生輕微振蕩，而在復合控制中這種現象幾乎沒有，如圖8所示。控制變量δx和δz的響應曲線見圖11～圖12，跟蹤正弦命令時，復合控制下的δx1未發生飽和且很快收斂，而僅襟翼控制下的δx2在整個仿真過程中經常發生飽和且持續振蕩。同樣，復合控制下的δz1非常平滑，而襟翼控制下的δz2有輕微振蕩現象。動態過程中，舵偏角δx1、δx2有一定程度的飽和，穩態時有小幅度的波動，從而將系統狀態穩定在滑模面上并收斂到原點，彌補了穩態過程中發動機關機所造成的穩態誤差。側噴發動機只在動態過程(初始階段)中工作，穩態時一直處于關機狀態，避免了過多的燃料消耗和擾動，如圖13所示。

圖8 攻角響應曲線(情形2)Fig.8 Response curve of the angle of attack (Case 2)

圖9 滾轉角響應曲線(情形2)Fig.9 Response curve of the roll angle (Case 2)

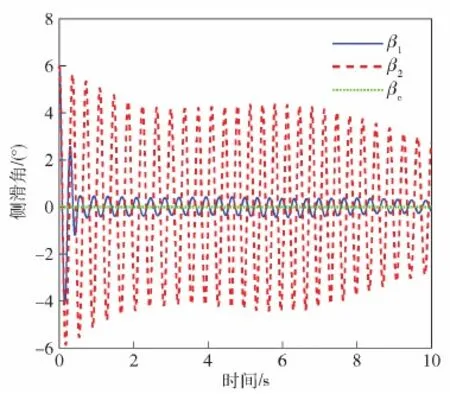
圖10 側滑角響應曲線(情形2)Fig.10 Response curve of the sideslip angle (Case 2)

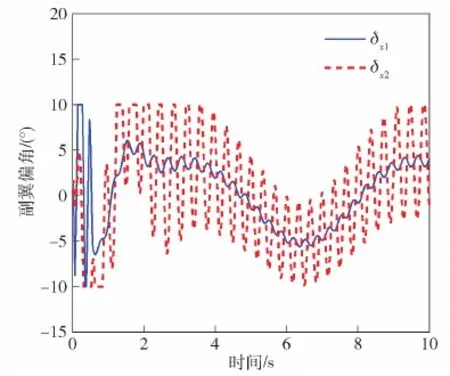
圖11 副翼響應曲線(情形2)Fig.11 Response curve of aileron (Case 2)

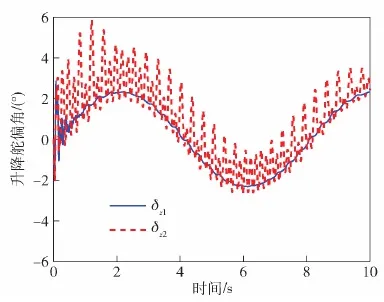
圖12 升降舵響應曲線(情形2)Fig.12 Response curve of elevator (Case 2)

圖13 直接側向力響應曲線(情形2)Fig.13 Response curve of lateral jets (Case 2)

5 結論

本文在襟翼飛行器的偏航通道中引入一對姿控發動機，構成了一種直接側向力與氣動力復合控制系統。通過將側滑角限制在0°附近，使該非線性模型可以解耦和線性化為縱向運動子系統和側向運動子系統。縱向運動子系統中不存在直接力，采用線性二次型最優理論設計控制器。針對側向運動子系統，采用線性控制理論設計了關于副翼舵偏角的線性狀態反饋控制律，將此控制律設計結果代入側向運動子系統模型后產生一個新的受控對象。對于新的受控對象，進一步利用側噴發動機的開關控制來提高對側滑角的控制品質。結合側噴發動機的開關特性，應用滑模控制理論設計側噴發動機的控制律，并通過設計邊界層有效地消除了滑模控制系統的抖振。仿真結果驗證了所提出的控制方法的優良性能，即偏航通道抖振現象被明顯抑制，側滑角可快速收斂，并且攻角與滾轉角可實現對制導指令的平穩快速響應。