MEMS陀螺噪聲理論與模型綜述*
聶偉豪,焦 娟,劉夢(mèng)祥,姜 波,周 怡,蘇 巖
(南京理工大學(xué) 機(jī)械工程學(xué)院·南京·210094)
0 引 言
陀螺儀是測(cè)量載體相對(duì)慣性空間運(yùn)動(dòng)角速度和角度的傳感器,高性能的硅微機(jī)電系統(tǒng)(Micro Electro Mechanical Systems,MEMS)陀螺儀在慣性導(dǎo)航、制導(dǎo)、控制等領(lǐng)域中具有至關(guān)重要的作用。目前,國(guó)內(nèi)外MEMS陀螺大多工作在模態(tài)匹配閉環(huán)檢測(cè)模式下,以此提高陀螺的整體性能[1],如提升標(biāo)度因數(shù)穩(wěn)定性,獲得高機(jī)械靈敏度,同時(shí)不會(huì)過(guò)多地?fù)p失測(cè)量帶寬。但是,陀螺閉環(huán)檢測(cè)與控制電路是復(fù)雜的機(jī)電混合系統(tǒng),系統(tǒng)中的噪聲源一旦變多,多種噪聲源共同引起諧振時(shí)信號(hào)相位和幅度的抖動(dòng)。因此需要研究陀螺各部分噪聲產(chǎn)生機(jī)理,構(gòu)建陀螺閉環(huán)系統(tǒng)的相位噪聲模型和幅度噪聲模型,從而對(duì)MEMS陀螺噪聲性能進(jìn)行評(píng)估與預(yù)測(cè)。本文主要圍繞MEMS陀螺噪聲源理論分析和系統(tǒng)噪聲模型的構(gòu)建展開調(diào)研,分析討論了國(guó)內(nèi)外研究機(jī)構(gòu)在MEMS陀螺噪聲理論研究與噪聲模型構(gòu)建上的思路和進(jìn)展,為后續(xù)提高M(jìn)EMS陀螺噪聲性能提供參考。
1 MEMS陀螺噪聲理論研究
1.1 MEMS陀螺噪聲表征方法
噪聲是一個(gè)隨機(jī)過(guò)程,通常使用一定時(shí)間段內(nèi)信號(hào)幅度平方的平均值來(lái)表示。噪聲在頻域上主要使用功率譜密度函數(shù)來(lái)表征,體現(xiàn)在主譜線兩旁連續(xù)分布的噪聲邊帶,具有頻譜不純凈的特點(diǎn)。另一種常用的表征方法為Allan方差[2],能夠直觀地反映MEMS陀螺的性能水平。一般情況下兩種表征方法可以相互轉(zhuǎn)換。與Allan方差相聯(lián)系的隨機(jī)漂移誤差源包括:零偏不穩(wěn)定性(Bias Instability,BIS)、量化噪聲、角度隨機(jī)游走(Angular Random Walk,ARW)、速率隨機(jī)游走(Rate Random Walk,RRW)、速率斜坡。這五種誤差源在Allan方差圖中具有不同的斜率,如圖1所示。零偏不穩(wěn)定性和角度隨機(jī)游走是力平衡模式下的主要性能指標(biāo),當(dāng)對(duì)角速率速度信號(hào)進(jìn)行積分時(shí),角度誤差的標(biāo)準(zhǔn)差最開始由角度隨機(jī)游走占主導(dǎo),當(dāng)積分時(shí)間變大,零偏不穩(wěn)定性成為主要因素。

圖1 Allan方差各誤差源Fig.1 Error sources of Allan variance
1.2 MEMS陀螺諧振系統(tǒng)中的噪聲源
在MEMS陀螺結(jié)構(gòu)以及測(cè)控電路構(gòu)成的諧振系統(tǒng)中包含多個(gè)噪聲源,如機(jī)械熱噪聲、前端放大器噪聲、偏置電壓噪聲等,這些噪聲源基本上由熱噪聲和閃頻噪聲構(gòu)成。MEMS陀螺及電路中的熱噪聲決定了角度隨機(jī)游走,電路中晶體管、場(chǎng)效應(yīng)管等器件產(chǎn)生的閃頻噪聲決定了陀螺零偏不穩(wěn)定性,所以將各噪聲源分為熱噪聲與閃頻噪聲進(jìn)行概述。
1.2.1 MEMS陀螺熱噪聲研究
由于硅微諧振式陀螺儀結(jié)構(gòu)尺寸非常小,封裝腔內(nèi)氣體分子的無(wú)規(guī)則運(yùn)動(dòng)會(huì)對(duì)可動(dòng)結(jié)構(gòu),如檢測(cè)質(zhì)量塊、諧振梁等產(chǎn)生碰撞,從而形成機(jī)械熱噪聲。機(jī)械熱噪聲會(huì)產(chǎn)生在敏感檢測(cè)方向的振動(dòng),作用效果與科氏力相同,會(huì)被接口電路檢測(cè)為角速度輸入。但是,機(jī)械熱噪聲產(chǎn)生的振動(dòng)極其微弱,沒(méi)有辦法直接測(cè)量,需要經(jīng)過(guò)接口電路對(duì)信號(hào)進(jìn)行放大,與此同時(shí)又會(huì)引入前端放大器輸入噪聲。多種噪聲使噪聲分析變得復(fù)雜,所以不斷地有學(xué)者對(duì)機(jī)械熱噪聲結(jié)合其他類型噪聲在測(cè)控電路中的傳遞過(guò)程和噪聲模型的構(gòu)建進(jìn)行研究。最早在1993年,T. B. Gabrielson[3]比較系統(tǒng)地研究了機(jī)械熱噪聲,并應(yīng)用等效電學(xué)模型來(lái)分析,他闡述了機(jī)械熱噪聲只取決于溫度和機(jī)械阻尼的大小,是一種白噪聲,功率譜密度在整個(gè)頻帶內(nèi)是均勻的,可以等效為沿著阻尼方向施加的大小隨機(jī)的力,其功率譜密度如下
(1)
式中,kB為玻耳茲曼常數(shù),T為絕對(duì)溫度,c0為阻尼系數(shù),Q為品質(zhì)因數(shù),m為陀螺結(jié)構(gòu)質(zhì)量,ω0為諧振頻率。同樣,電路中的電阻和晶體管也會(huì)由于內(nèi)部帶電載流子的無(wú)規(guī)則運(yùn)動(dòng),向電路引入熱噪聲。電阻熱噪聲可以用一個(gè)電壓源來(lái)模擬,晶體管熱噪聲主要在溝道中產(chǎn)生,可以用一個(gè)連接源漏兩端的電流源來(lái)模擬,兩者的功率譜密度為
SR(f)=4kBTR
(2)
SM(f)=4kBTγgm
(3)
式中,R為電阻值,γ為溝道深寬比相關(guān)的常系數(shù),長(zhǎng)溝道晶體管為2/3,gm為晶體管跨導(dǎo),f為頻率。
隨后,V. Annovazzi-Lodi[4]等將機(jī)械熱噪聲代入陀螺兩個(gè)軸的動(dòng)力學(xué)方程中,同時(shí)考慮了電熱噪聲的影響,計(jì)算出陀螺的信噪比,并引入噪聲等效角速率(Noise Equivalent Angular Rate,NER)這個(gè)參數(shù)來(lái)同時(shí)表征陀螺的噪聲性能與靈敏度限制,研究發(fā)現(xiàn)機(jī)械熱噪聲可能代表傳感器實(shí)際靈敏度的極限。2005年,阿拉巴馬大學(xué)R. P. Leland[5]首先構(gòu)建了機(jī)械熱噪聲在MEMS陀螺控制環(huán)路中傳遞過(guò)程的數(shù)學(xué)表達(dá)式,使用隨機(jī)平均法得到開環(huán)和力平衡模式下“慢”變量表示的近似系統(tǒng)來(lái)分析機(jī)械熱噪聲的影響,給出了模態(tài)匹配和頻率裂解下角度隨機(jī)游走和噪聲等效角速率的功率譜密度之間的關(guān)系,在給定結(jié)構(gòu)參數(shù)下計(jì)算出的角度隨機(jī)游走水平達(dá)到了戰(zhàn)術(shù)級(jí)。
1.2.2 MEMS陀螺閃頻噪聲研究
閃頻噪聲即1/f噪聲,頻率越高功率譜密度越小。與白噪聲不同,閃頻噪聲無(wú)法通過(guò)對(duì)輸出數(shù)據(jù)進(jìn)行平均而降低,而且由于這種噪聲在低頻處能量集中,信號(hào)經(jīng)過(guò)積分產(chǎn)生的角度誤差會(huì)隨著時(shí)間積累,對(duì)導(dǎo)航精度產(chǎn)生很大影響。閃頻噪聲來(lái)源于CMOS晶體管柵氧化層與硅襯底界面處電荷載流子的隨機(jī)俘獲和釋放,是所有晶體管的固有特性[6]。在硅微陀螺儀復(fù)雜的測(cè)控電路中,存在成百上千的晶體管,且不同晶體管的噪聲轉(zhuǎn)化機(jī)理也不盡相同,從眾多含有晶體管電路中定位出影響硅微陀螺零偏不穩(wěn)定性的主導(dǎo)噪聲源就顯得十分困難。晶體管的閃頻聲通常用一個(gè)與柵極串聯(lián)的電壓源來(lái)模擬
(4)
式中,Cox為單位面積的柵極氧化層電容,K為由工藝決定的常量,W,L分別為晶體管溝道的寬度和長(zhǎng)度。
2001年,懷俄明大學(xué)S.C.Peacock[7]基于場(chǎng)效應(yīng)晶體管放大器研究了1/f噪聲影響增益的幅度和相位,將其轉(zhuǎn)換為載波信號(hào)上的振幅調(diào)制噪聲和相位調(diào)制噪聲。A. Mohammadi等[8]在2012年發(fā)表的文獻(xiàn)中指出電熱噪聲和閃頻噪聲是批量加工的MEMS陀螺中的主要噪聲,并提出一種低閃頻噪聲的接口電路。同年,M. Kirkko-Jaakkola[9]將1/f噪聲的特性與陀螺偏置校準(zhǔn)中涉及的預(yù)測(cè)問(wèn)題聯(lián)系起來(lái),利用卡爾曼預(yù)測(cè)器和移動(dòng)平均預(yù)測(cè)器來(lái)預(yù)測(cè)零偏。2017年,德國(guó)博世公司T. Hiller等[10]討論了具有力平衡和正交控制回路的陀螺噪聲性能,發(fā)現(xiàn)零偏不穩(wěn)定性在長(zhǎng)積分時(shí)間內(nèi)主導(dǎo)了角度誤差,即1/f噪聲是主要誤差分量,并證明零偏不穩(wěn)定性與正交誤差不具有相關(guān)性。為了尋找主導(dǎo)零偏不穩(wěn)定性的1/f來(lái)源,他們通過(guò)理論分析和測(cè)試數(shù)據(jù)得出零偏不穩(wěn)定性隨著驅(qū)動(dòng)振幅的增大而增加,隨頻差增大而降低,并不是獨(dú)立產(chǎn)生于敏感回路,并給出了幾個(gè)零偏不穩(wěn)定性可能的來(lái)源,包括:通過(guò)力作用于檢測(cè)質(zhì)量塊的噪聲源,通過(guò)饋通產(chǎn)生交叉耦合的噪聲源,以及來(lái)自驅(qū)動(dòng)回路鎖相環(huán)(Phase-Locked Loop,PLL)的解調(diào)信號(hào)的相位抖動(dòng),如圖2所示。隨后又在2019年發(fā)表的論文[11]中驗(yàn)證之前的猜想,分析了附加于頻率調(diào)諧電壓上的閃頻噪聲會(huì)影響零偏不穩(wěn)定性,并且交叉耦合到輸出的傳遞函數(shù),比輸入角速率到輸出的傳遞函數(shù)在驅(qū)動(dòng)頻率處具有更陡峭的相位梯度,進(jìn)一步通過(guò)實(shí)驗(yàn)證明DAC施加于頻率調(diào)諧電壓上的1/f噪聲使交叉耦合信號(hào)在驅(qū)動(dòng)頻率附近產(chǎn)生噪聲邊帶,從而主導(dǎo)了零偏不穩(wěn)定性。

圖2 博世公司提出的閉環(huán)控制下陀螺零偏不穩(wěn)定性的可能來(lái)源Fig.2 Possible sources of gyro bias instability under closed-loop control proposed by Bosch Company

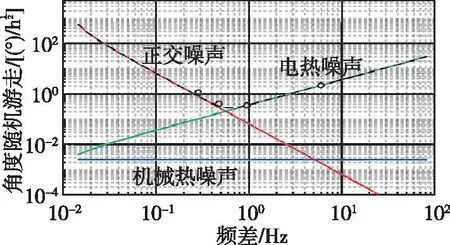
圖3 加州大學(xué)歐文分校由不同噪聲源估計(jì)的ARW極限Fig.3 Estimated ARW limit of the gyroscope due to different noise sources
2 MEMS陀螺噪聲模型研究進(jìn)展
進(jìn)行噪聲分析的重要手段是噪聲模型的建立,將各器件或者模塊的噪聲傳遞過(guò)程連結(jié)起來(lái)可以得到整個(gè)系統(tǒng)的噪聲模型,通過(guò)對(duì)諧振器系統(tǒng)噪聲模型的分析,可以得出系統(tǒng)的噪聲特性。但是為了實(shí)現(xiàn)高精度測(cè)量,測(cè)控系統(tǒng)變得復(fù)雜多樣,噪聲源增多,特別是在模態(tài)匹配、閉環(huán)檢測(cè)形成的多閉環(huán)系統(tǒng)中,對(duì)各噪聲源的分析較為困難,不同類型的噪聲源經(jīng)過(guò)諧振器會(huì)影響信號(hào)的幅度和相位。
為了使不同的實(shí)際噪聲源在統(tǒng)一的模型框架下進(jìn)行傳遞,A.Hajimiri將對(duì)象系統(tǒng)分解為幅度和相位兩個(gè)子系統(tǒng),引入了沖擊敏感函數(shù)(Impact Sensitive Function,ISF)來(lái)描述不同時(shí)刻輸入的脈沖電流噪聲對(duì)輸出電壓幅值和相位波動(dòng)的影響。隨后,D.Ham 與A.Hajimiri[13]一起提出以虛擬阻尼作為相位噪聲的度量,把振蕩器相位噪聲理論和諧振器理論放在相同的框架內(nèi)。南京理工大學(xué)趙健等[14]將噪聲分解的方法應(yīng)用于MEMS諧振器中,將加性噪聲源和乘性噪聲源通過(guò)諧振器分解的調(diào)制矩陣得到幅度噪聲和相位噪聲,分解后的噪聲源通過(guò)同樣被分解的幅度和相位子系統(tǒng)得到幅度抖動(dòng)和相位抖動(dòng),并對(duì)噪聲分解模型進(jìn)行仿真與實(shí)驗(yàn)驗(yàn)證。2018年B.Hong與A.Hajimiri[15]發(fā)表的論文中完善了包含振幅衰減和相位轉(zhuǎn)化的非線性振幅擾動(dòng)和相位擾動(dòng)表達(dá)式。分解后的系統(tǒng)相比原系統(tǒng),階數(shù)得以降低,對(duì)象足夠簡(jiǎn)化,單獨(dú)分析噪聲對(duì)信號(hào)幅度和相位的影響,分解原理如下:
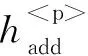
(5)
(6)
(7)
(8)
式中,τ為沖激時(shí)刻,指數(shù)衰減函數(shù)為
(9)
(10)
式中,Km為在諧振頻率處諧振器的增益,u(t)表示載波信號(hào)。
式(9)和式(10)可以看作噪聲響應(yīng)在理想振幅矢量的切向(振幅變化方向) 和法向 (相位變化方向) 的投影,從中可以得到分解后諧振器幅度調(diào)制和相位調(diào)制子系統(tǒng)的傳遞函數(shù)。由此,可以定義一個(gè)調(diào)制矩陣M,用來(lái)將完整模型中的加性噪聲和乘性噪聲分解到相位調(diào)制和幅度調(diào)制子系統(tǒng)中,得到的相位調(diào)制及幅度調(diào)制噪聲,施加在分解后的傳遞函數(shù)上,最終得出諧振器系統(tǒng)幅度和相位的噪聲響應(yīng),過(guò)程如圖4所示。基于以上理論,將MEMS陀螺的噪聲建模劃分為相位噪聲模型與幅度噪聲模型的構(gòu)建。

(a) 諧振器復(fù)平面的噪聲響應(yīng)
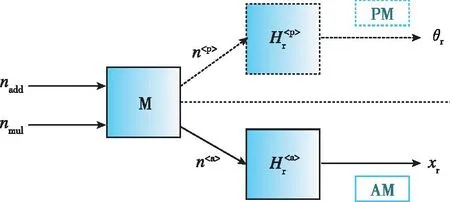
(b) 分解的諧振器噪聲傳遞過(guò)程圖4 相位與幅度噪聲分解過(guò)程Fig.4 Decomposition process of phase and amplitude noise
2.1 相位噪聲模型研究進(jìn)展
諧振器系統(tǒng)中的噪聲源會(huì)引起諧振器頻率或相位抖動(dòng),產(chǎn)生相位噪聲。建立相位噪聲模型,分析相位噪聲理論上對(duì)陀螺零偏輸出的影響,在傳感器設(shè)計(jì)階段具有十分重要的意義。針對(duì)不同的諧振器類型,先后提出線性時(shí)不變(Linear Time-invariant,LTI)模型、線性時(shí)變(Linear Time-Varying,LTV)模型以及非線性相位噪聲模型。
2.1.1 傳統(tǒng)振蕩器相位噪聲模型發(fā)展過(guò)程
最早在1966年,D.B.Leeson[16]提出了基于線性反饋系統(tǒng)的線性時(shí)不變相位噪聲模型,如圖5所示,構(gòu)建了從放大器輸入噪聲功率譜密度到輸出相位噪聲的傳遞過(guò)程,稱為L(zhǎng)eeson公式,其表達(dá)式為
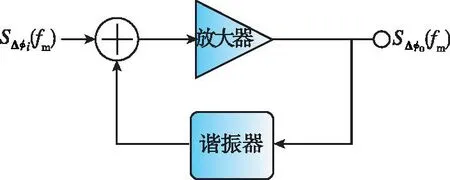
圖5 Leeson相位噪聲模型Fig.5 Leeson phase noise model
(11)
式中,F(xiàn)為放大器噪聲系數(shù),Ps為載波功率,fc為熱噪聲與1/f噪聲轉(zhuǎn)折頻率,f0為諧振頻率,QL為有載品質(zhì)因數(shù),是表征振蕩器相位噪聲指標(biāo)的參數(shù)。
Leeson公式作為L(zhǎng)TI模型的基礎(chǔ),不斷有人對(duì)其進(jìn)行引用及補(bǔ)充。1996年B.Razavi[17]研究了噪聲源被帶有振蕩器的反饋系統(tǒng)整形后輸出噪聲功率譜密度的過(guò)程,重新定義了有載品質(zhì)因數(shù),并且分析了三種噪聲的特性,即加性噪聲、低頻乘性噪聲、高頻乘性噪聲,計(jì)算的環(huán)形振蕩器相位噪聲的理論仿真值和測(cè)量值誤差不超過(guò)5dB/Hz。但是基于LTI假設(shè)的模型不能解釋相位譜中的閃頻噪聲、1/f3噪聲,并且未考慮噪聲調(diào)幅到調(diào)相的變換過(guò)程,還包含經(jīng)驗(yàn)參數(shù),幾乎無(wú)法對(duì)指定振蕩器噪聲進(jìn)行準(zhǔn)確的預(yù)測(cè)。
為了彌補(bǔ)線性時(shí)不變相位噪聲模型的缺陷,A.Hajimiri等[19]T.H.Lee等[19]提出了振蕩器的線性時(shí)變相位噪聲模型,利用ISF推導(dǎo)了環(huán)形振蕩器在給定的總功率損耗與振蕩頻率下抖動(dòng)和相位噪聲的閉環(huán)表達(dá)式。研究發(fā)現(xiàn)輸出噪聲功率譜密度由各部分噪聲在振蕩頻率整數(shù)倍附近的相位噪聲之和給出,并證明了相位譜中的閃爍頻率噪聲是由電路中非對(duì)稱因素引起的。LTV模型預(yù)測(cè)實(shí)際相位噪聲需要確定沖擊敏感函數(shù),但 ISF并沒(méi)有直接與振蕩器的電路物理參數(shù)相關(guān)聯(lián),限制了該模型在電路設(shè)計(jì)中的應(yīng)用。2000年,A.Demir[20]對(duì)線性時(shí)變模型進(jìn)行改進(jìn),將噪聲擾動(dòng)引入振蕩器的微分方程中,采用Floquet理論得到振蕩器的周期穩(wěn)態(tài)解,并將相位噪聲視作相位偏移對(duì)周期穩(wěn)態(tài)解的調(diào)制,得到在頻偏處的單邊帶功率譜密度。之后他又提出冪律譜噪聲模型[21],使用各種符合冪律譜函數(shù)的噪聲分量之和來(lái)表征振蕩器信號(hào)的相位起伏譜密度。2010年,M.Q.Lee[22]根據(jù)閉環(huán)增益參數(shù)對(duì)反饋式振蕩器的穩(wěn)定性與相位噪聲進(jìn)行了研究。將 1/f噪聲視為直流附近的擾動(dòng)對(duì)器件參數(shù)的調(diào)制,利用 Kurokawa方法分析1/f噪聲到相位噪聲的變換。
2.1.2 非線性相位噪聲模型發(fā)展過(guò)程
無(wú)論對(duì)于LTI模型還是LTV模型,鑒于CMOS振蕩器的應(yīng)用場(chǎng)合,幅度抖動(dòng)對(duì)頻率的耦合作用均作為被忽略的因素處理。對(duì)于MEMS振蕩器,由于非線性剛度的存在,幅度與頻率之間存在一個(gè)不可被忽略的耦合路徑,因此上述模型均無(wú)法直接應(yīng)用于MEMS振蕩器。密歇根大學(xué)S. Lee等[23]研究發(fā)現(xiàn)MEMS諧振器中振幅-剛度耦合(Amplitude-Stiffness,A-S)效應(yīng)會(huì)導(dǎo)致額外的1/f3相位噪聲,產(chǎn)生的1/f3噪聲與低于臨界振幅的振幅無(wú)關(guān)。為了探究非線性剛度下低頻域相位噪聲產(chǎn)生機(jī)制,研究人員相繼提出新的相位噪聲模型。
2010年,新加坡國(guó)立大學(xué)賀林[24]等人提出了狀態(tài)空間相位噪聲模型,將 LTV 模型與 A-S 效應(yīng)相結(jié)合,使用自動(dòng)幅度控制回路(Automatic Amplitude Control Loop,AAC)避免軌道擾動(dòng)被積分產(chǎn)生漂移,如圖6(a)所示。將位移傳感器檢測(cè)到的振蕩幅值與預(yù)設(shè)值進(jìn)行比較,它們的差值被送入AAC環(huán)路濾波器L(s),以產(chǎn)生增益擾動(dòng)信號(hào),得到相位噪聲的封閉解。其中,AAC引入的1/f噪聲通過(guò)A-S效應(yīng)產(chǎn)生1/f3相位噪聲。2011年,美國(guó)Draper實(shí)驗(yàn)室建立了閉環(huán)下諧振器噪聲和電路噪聲以及幅度頻率耦合導(dǎo)致的頻率噪聲到輸出相位噪聲功率譜密度的傳遞過(guò)程[25],并且額外分析了MEMS諧振器系統(tǒng)的參數(shù)調(diào)制的影響,如圖6(b)所示。參數(shù)抖動(dòng)由振幅噪聲、電壓源擾動(dòng)和溫度等因素導(dǎo)致,不僅使上述三種噪聲分量出現(xiàn)額外的相位噪聲,還導(dǎo)致加性噪聲電壓和相位之間的直接耦合使閃頻噪聲在相位噪聲譜中產(chǎn)生1/f3噪聲。研究還發(fā)現(xiàn),電路非線性使近載波相位噪聲顯著增加,且由于1/f到諧振器的非線性映射,拐角頻率會(huì)降低到1/10,如果再加入諧振器非線性,相位噪聲會(huì)進(jìn)一步增加。2013年,南京理工大學(xué)石然[26]對(duì)傳統(tǒng) LTI 模型進(jìn)行修正并考慮A-S效應(yīng)引起的額外相位噪聲,如圖6(c)所示。他分析了振蕩器中自動(dòng)增益控制(Automatic Gain Control,AGC)電路對(duì)低頻范圍內(nèi)相位噪聲(1/f3相位噪聲和1/f5相位噪聲)的影響,指出AGC噪聲與跨阻放大器輸出電壓信號(hào)相乘會(huì)導(dǎo)致噪聲頻譜的搬移,產(chǎn)生1/f3與1/f5相位噪聲,在滿足帶寬條件下,調(diào)整驅(qū)動(dòng)振幅和Q值可以有效降低相位噪聲。將實(shí)驗(yàn)結(jié)果與噪聲模型預(yù)測(cè)對(duì)比,白相位噪聲和1/f5相位噪聲的測(cè)試數(shù)據(jù)比模型預(yù)測(cè)值低約10dB。與之前的模型相比,相位噪聲模型與實(shí)驗(yàn)結(jié)果更加吻合。2014年,D.K. Agrawal等[27]在其發(fā)表的論文中更全面地分析了來(lái)自機(jī)械結(jié)構(gòu)和電路模塊非線性效應(yīng)引起的相位噪聲,研究發(fā)現(xiàn)靠近載波頻率的相位噪聲受非線性影響非常嚴(yán)重。另外,引入了擴(kuò)散系數(shù)作為定性參數(shù)來(lái)量化振蕩器中的相位噪聲,擴(kuò)散系數(shù)與剛度硬化系數(shù)和剛度軟化系數(shù)成比例,可以通過(guò)調(diào)節(jié)電剛度減小非線性,來(lái)找到最優(yōu)擴(kuò)散系數(shù),但是在噪聲模型中沒(méi)有考慮由非線性導(dǎo)致的1/f的轉(zhuǎn)換。2019年,M.Bonnin等[28]研究了有色噪聲對(duì)非線性振蕩器中相位噪聲的影響,將受有色噪聲影響的非線性系統(tǒng),轉(zhuǎn)換為受高斯白噪聲影響的等效系統(tǒng),對(duì)變換系統(tǒng)的相位偏差和振幅偏差進(jìn)行了描述,其中系統(tǒng)動(dòng)力學(xué)僅用相位變量來(lái)描述,推導(dǎo)了一個(gè)簡(jiǎn)化的相位模型來(lái)分析和表征相位噪聲,實(shí)現(xiàn)了更精準(zhǔn)的預(yù)測(cè)。2021年,南京理工大學(xué)劉夢(mèng)祥等[29]提出了包括AGC電路和頻率讀出電路在內(nèi)的全相位噪聲系統(tǒng)模型,如圖6(d)所示。結(jié)合電路仿真軟件模擬晶體管噪聲加入到仿真模型進(jìn)行仿真,揭示調(diào)頻陀螺儀中所有不同的物理噪聲源,并量化它們的權(quán)重,在高頻域量化噪聲占主導(dǎo),在低頻域結(jié)構(gòu)中熱噪聲和AGC噪聲共同影響預(yù)測(cè)的性能,測(cè)試的零偏不穩(wěn)定性為1.4(°)/h,預(yù)測(cè)的零偏不穩(wěn)定性為1.1(°)/h,相位噪聲模型為陀螺儀系統(tǒng)設(shè)計(jì)和CMOS電路設(shè)計(jì)提供了定量的指導(dǎo)。

(a) 狀態(tài)空間形式的相位噪聲模型
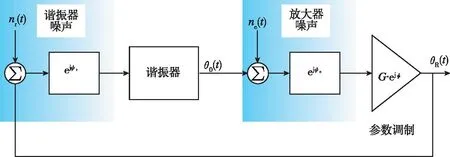
(b) Draper實(shí)驗(yàn)室諧振器相位噪聲閉環(huán)傳遞
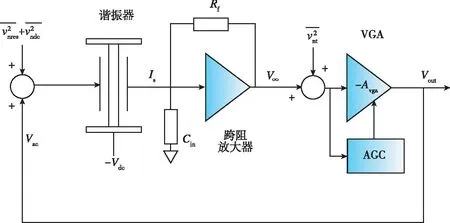
(c) 帶有AGC的諧振器相位噪聲傳遞過(guò)程
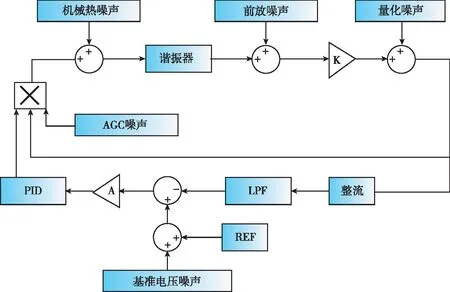
(d) FM陀螺的相位噪聲模型圖6 非線性相位噪聲模型Fig.6 Nonlinear phase noise model
2.2 幅度噪聲模型研究進(jìn)展
MEMS陀螺的閉環(huán)驅(qū)動(dòng)具有自動(dòng)幅度控制環(huán)路以確保恒幅振蕩,所以驅(qū)動(dòng)軸的振幅穩(wěn)定性相對(duì)較好,驅(qū)動(dòng)信號(hào)對(duì)解調(diào)信號(hào)的噪聲貢獻(xiàn)一般可以忽略,常用的幅度噪聲模型主要是針對(duì)檢測(cè)軸諧振系統(tǒng)建立。由于FPGA中的調(diào)制和解調(diào)模塊使得電路的閃頻噪聲幾乎不影響檢測(cè)輸出,陀螺儀帶寬中的電路噪聲可視為白噪聲。在力平衡閉環(huán)檢測(cè)下,推導(dǎo)出諧振器、測(cè)控電路各部分傳遞函數(shù)和角速率輸出處各噪聲源的頻譜表達(dá)式,而計(jì)算出角度隨機(jī)游走性能指標(biāo)。這樣的理論分析方法還能反映單個(gè)噪聲源對(duì)輸出噪聲等效率的貢獻(xiàn),分析隨著陀螺結(jié)構(gòu)和電路參數(shù)變化的不同趨勢(shì),量化這些噪聲對(duì)輸出端噪聲性能的影響,能夠?qū)?yōu)化實(shí)際電路提供參考。


(a) 加州大學(xué)洛杉磯分校提出的力平衡噪聲模型

(b) 南京理工大學(xué)提出的開環(huán)檢測(cè)噪聲模型

(c) 東南大學(xué)提出的噪聲模型
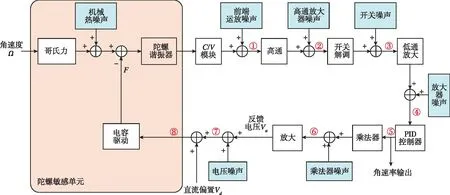
(d) 國(guó)防科技大學(xué)提出的嵌套環(huán)陀螺噪聲模型
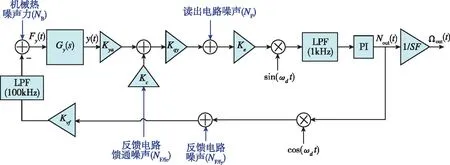
(e) 蘇州大學(xué)提出的基于EAM檢測(cè)的噪聲模型圖7 各種幅度噪聲模型Fig.7 Various amplitude noise models


幅度噪聲模型的構(gòu)建過(guò)程基本是針對(duì)力平衡閉環(huán),在環(huán)路不同位置加入實(shí)際噪聲源,使模型預(yù)測(cè)效果更加貼近測(cè)試結(jié)果,如表1所示。構(gòu)建噪聲模型一方面可以研究陀螺結(jié)構(gòu)以及電路參數(shù),如驅(qū)動(dòng)頻率、驅(qū)動(dòng)振幅、電路增益等對(duì)于輸出噪聲等效角速率的影響;一方面可以量化不同噪聲源對(duì)于輸出噪聲等效角速率的貢獻(xiàn),從而指導(dǎo)設(shè)計(jì),提高陀螺噪聲性能。

表1 各幅度噪聲模型預(yù)測(cè)效果對(duì)比Tab.1 Experimental performance index of each amplitude noise model
3 噪聲模型總結(jié)及展望
綜上所述,近年來(lái)隨著MEMS陀螺精度的不斷提高,對(duì)噪聲性能的要求也逐步提升,噪聲模型的構(gòu)建變得愈加重要。相位噪聲模型從LTI模型到考慮非線性因素的模型,已經(jīng)能夠很好地解釋各種低頻相位噪聲的產(chǎn)生機(jī)理,并對(duì)相位噪聲進(jìn)行準(zhǔn)確預(yù)測(cè),但是這些相位噪聲模型主要針對(duì)以頻率為輸出的諧振器,應(yīng)用于指定的環(huán)路,缺少相對(duì)統(tǒng)一的方法探明相位噪聲與陀螺性能指標(biāo)的關(guān)系。對(duì)于主流的調(diào)幅陀螺,由于相位噪聲對(duì)信號(hào)幅度耦合作用,以及解調(diào)過(guò)程相位噪聲對(duì)解調(diào)輸出的影響效果尚不清晰,目前并沒(méi)有一個(gè)系統(tǒng)化的相位噪聲模型來(lái)完整地解釋相位噪聲對(duì)零偏輸出的影響。幅度噪聲模型雖然基于諧振器系統(tǒng)各部分傳遞函數(shù),搭建各輸入噪聲與輸出噪聲等效角速率的數(shù)學(xué)關(guān)系,從中得到角度隨機(jī)游走影響因素,并能夠通過(guò)仿真及實(shí)驗(yàn)進(jìn)行驗(yàn)證。但是幅度噪聲模型對(duì)噪聲傳遞過(guò)程進(jìn)行了簡(jiǎn)化,僅以陀螺環(huán)路中的白噪聲為研究對(duì)象,缺少對(duì)零偏不穩(wěn)定性噪聲模型的建立。
針對(duì)這些問(wèn)題,本文認(rèn)為需要從以下兩個(gè)方面對(duì)噪聲模型進(jìn)行改進(jìn)。
1)通過(guò)建立相位噪聲模型探究相位噪聲對(duì)MEMS調(diào)幅陀螺角速率輸出的影響,并建立相位噪聲模型與陀螺性能之間的聯(lián)系。
2)深入對(duì)MEMS陀螺零偏不穩(wěn)定性來(lái)源的研究,并探究閃頻噪聲在陀螺系統(tǒng)傳遞過(guò)程中的機(jī)理。通過(guò)對(duì)零偏不穩(wěn)定性和閃頻噪聲特性的研究,搭建一個(gè)完整的幅度噪聲模型,以更好地理解陀螺系統(tǒng)中幅度噪聲的產(chǎn)生。
建立完整的噪聲模型不僅能夠量化各物理噪聲源對(duì)MEMS陀螺性能指標(biāo)的實(shí)際貢獻(xiàn),還能優(yōu)化陀螺結(jié)構(gòu)及電路設(shè)計(jì),使陀螺分辨率和精度得到大幅提高。

