基于數據融合的MEMS陣列加速度傳感器實現方法*

吳奇龍，周 同

(南京理工大學 機械工程學院·南京·210094)

0 引 言

工程技術的不斷發展以及對精密制造與精密測量技術需求的日益提高，極大地刺激著MEMS傳感器及數據處理技術的發展。盡管如此，依然存在著對寬頻帶、大范圍信號實時測量的高要求與傳感器有限檢測性能之間的矛盾。例如，在大型光學器件精密加工時，需要對機器人終端執行器跨越7個數量級(10-7g～1g，g表示重力加速度)的寬頻(1～500Hz)振動信號進行實時檢測以實現納米級原位測量及振動補償等關鍵技術環節，要求加速度傳感器具備低噪聲、寬頻帶、高動態范圍等性能。然而，已有的壓電式、諧振式、電容式和隧道電流式等MEMS加速度傳感器均無法同時滿足上述應用場景的技術需求。

近年來，芯片工藝的不斷迭代升級，推動了MCU主頻與算力的不斷增加，通過實時數據融合技術融合多個MEMS加速度計的互補性數據以獲得更可靠的數據已成為了提高對寬頻帶、大范圍信號振動信號檢測能力的新方案。MEMS加速度傳感器具有抗過載、體積小、質量小、成本低和易于集成等優點，適合陣列集成。陣列傳感器的性能一方面受制于各子傳感器的性能與契合度，另一方面受制于數據融合算法的性能。MEMS陣列加速度傳感器將用于振動信號的動態測量，因此，對數據融合算法的實時性和精度提出了較高的要求，例如，在機器人末端振動檢測的應用場景中，需要數據融合算法的融合輸出間隔小于1ms，且融合數據的精度不低于各個MEMS子傳感器的精度。

數據融合技術，也稱多傳感器數據融合技術，分為數據級融合、特征級融合和決策級融合三類[1]，MEMS陣列加速度傳感器采用數據級融合技術。現有的數據級融合技術可以歸納為以下三類：其一是加權平均法[2]、貝葉斯估計法[3]、卡爾曼濾波法[4]和最小二乘法[5]等經典融合方法，這類方法的實時性較好，但一般需要配合最優化技術或自適應策略以獲取較高的融合精度；其二是模糊控制法[6]、粗集理論法[7]、神經網絡法[8-9]，這類方法的穩健性較高，能夠融合不同類型或差異較大的傳感器數據，缺點是模型復雜、融合精度和實時性之間相互制約；其三是證據理論[10]、支持度評估等與上述方法的雜交變體，也是近年來多傳感器數據融合領域的研究熱點，例如加權融合與卡爾曼濾波結合[11]、信任度與遺傳算法結合[12]等方法，這類方法能在數據源存在較大干擾的情況下使融合數據維持較高的可信度，但該方法依賴大量的傳感器節點且實時性低。因此，上述眾多已有的數據融合方法均無法滿足本文MEMS陣列加速度傳感器對數據融合算法的精度與實時性要求。

針對單MEMS加速度計性能有限，其采集到的信息往往無法滿足實際工程中復雜且嚴苛的檢測需求的問題，本文設計一種MEMS陣列加速度傳感器的系統架構，并針對已有的數據融合技術無法滿足MEMS陣列加速度傳感器的精度與實時性要求的問題，提出基于離散對數映射的自整定加權融合算法。在此基礎上，設計MEMS陣列加速度傳感器的實現方法與仿真驗證方案。

1 MEMS陣列加速度傳感器系統設計

MEMS陣列加速度傳感器主要由MEMS加速度傳感器陣列和微控制單元(Microcontroller Unit，MCU)兩部分組成，其系統架構如圖1所示。其中，MEMS陣列模塊由多個(本文以3個為例)具有互補范圍的MEMS加速度計組成，在通道使能信號的控制下，為MCU提供指定通道(子傳感器)的數據；在工作模式下，MCU將輸出通道使能信號并采集兩個通道的加速度數據，然后對采集到的數據進行野值修正、溫度補償等必要的預處理操作，對數尺度權重映射策略模型將根據輸入數據的范圍情況輸出數據融合權重，最后，數據融合模型將對融合預處理后的雙通道數據加權以獲得輸出值，同時數據通道決策控制模塊將根據融合輸出值產生新的通道使能信號；在標定模式下，MCU根據輸入的標定參考值計算融合數據的損失值，進而在線整定對數尺度權重映射策略的模型參數。通道使能信號采用一位二進制表示，其為0時，使能加速計1和2；為1時，使能加速度傳感器2和3。

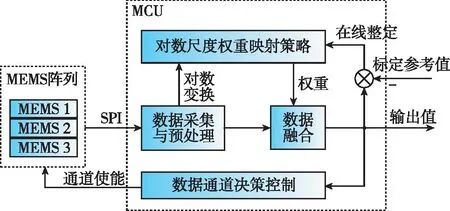
圖1 MEMS陣列加速度傳感器系統架構框圖Fig.1 Frame of the MEMS array acceleration sensor

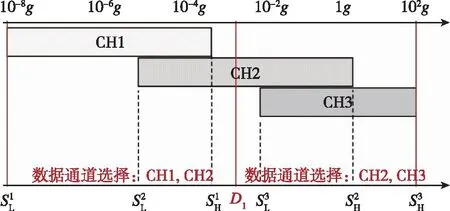
圖2 MEMS陣列加速度傳感器互補范圍示意圖Fig.2 Schematic of the complementary range of MEMS array acceleration sensor

2 基于離散對數映射的自整定加權融合算法

低延時、高精度的數據融合算法是MEMS陣列加速度傳感器的關鍵技術需求。加權平均數據融合方法是根據經驗賦予各個數據源合適的權重系數以獲得更高質量的數據輸出，該方法具有原理簡單、實時性高的優點，因此本文將基于加權融合法對采集到的雙通道數據進行實時融合，雙通道數據加權融合公式如下

d=dL×ω+dH×(1-ω)

(1)

式中，dH和dL為采集的雙通道數據，d為融合輸出數據，ω為雙通道加權融合的權重。

權重設計是加權融合法的關鍵環節，決定著加權融合算法的性能。近年來相關研究中的權重設計方法可以歸納為以下兩類：其一是利用噪聲分析、支持度分析等技術自適應生成融合權重的在線方法[13]，此類方法的計算過程復雜，實時性較低；其二是粒子群優化等技術生成最優權重向量的離線方法[14]，這類方法幾乎不損失融合速度，缺點是依賴離線訓練過程且收斂困難。為了在不損失加權融合實時性且不依賴離線優化過程的前提下提高融合精度，本文提出了基于離散對數映射的自整定加權融合算法。該算法在工作模式時將根據數據狀態快速給出融合權重，在標定模式時將根據標定參考值計算融合輸出的損失值進而實現權重自整定。為避免數據范圍對權重自整定過程的影響，本文使用相對誤差的平方δ2作為損失值，損失函數如下

(2)

算法1描述了離散對數尺度權重映射及自整定算法的具體流程。其中，N是MEMS陣列加速度傳感器的工作范圍在對數尺度上的等分區間個數，較大的N有利于提高融合精度，但會降低權重自整定的收斂難度和收斂效果，反之亦然；α是ω每次調整的步長，較大的α將提高權重自整定的收斂速度，但會降低收斂的精度和穩定性，反之亦然；K是權重更新的平滑步數，恰當的K將提高算法的魯棒性，避免算法易受到噪聲或異常數據的干擾而無法收斂。

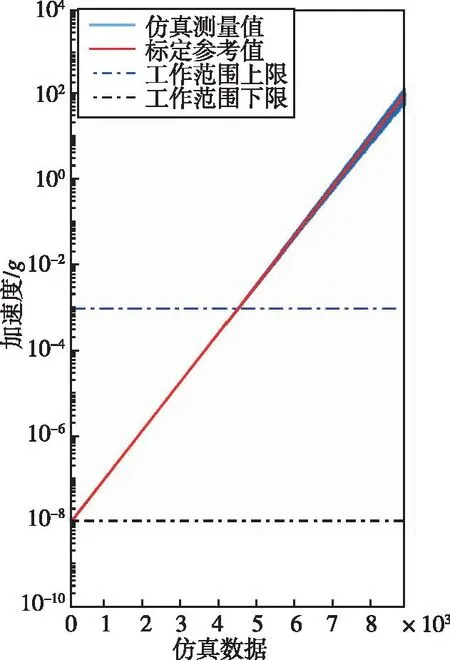
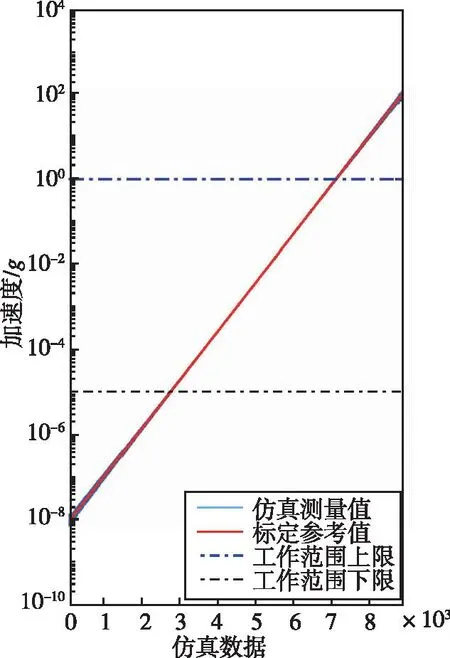
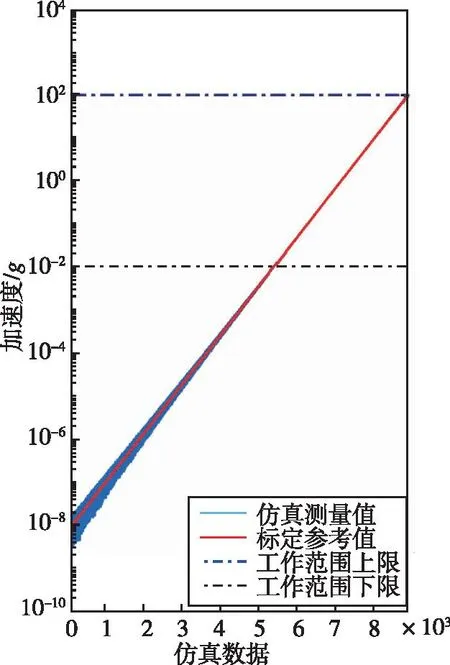
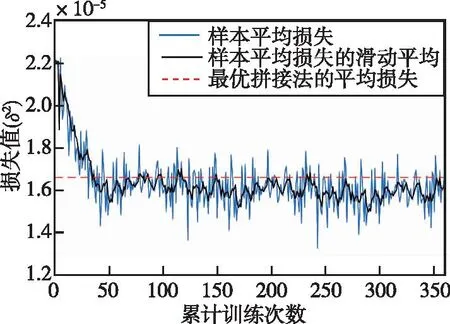
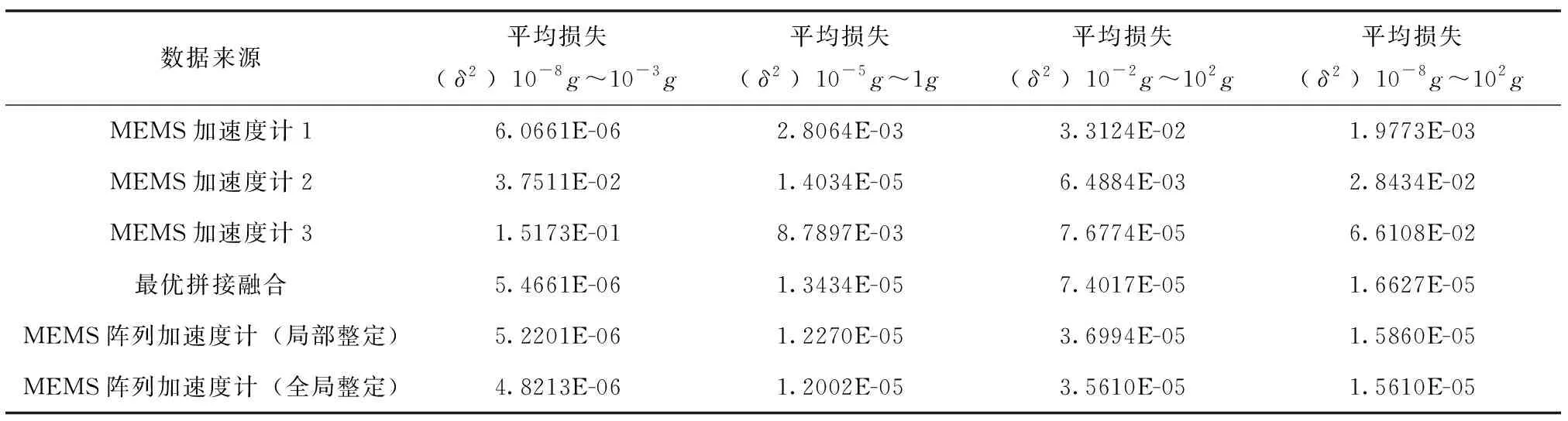
算法1:離散對數尺度權重映射及自整定流程Algorithm 1:Discrete logarithmic scale weight mapping and self-tuning process參數設置:區間個數N,調整步長α,平滑步數K初始化:融合權重Ω=(ω1,ω2,…,ωN),區間閾值Τ=(τ1,τ2,…,τN-1),經驗回放池GN×K×2=?輸入:對數尺度Sc=logdL+dH2 ,標定參考值R(可選,缺省值為inf)輸出:融合權重ωWhileR≠inf i=count(τi∈Τ∩τi

3 仿真實驗與結果分析

為了驗證本文MEMS陣列加速度傳感器實現方法的可行性，設計了三個不同工作范圍的MEMS加速度計。假設三個MEMS加速度計的工作范圍分別為10-8g～10-3g、10-5g～1g、10-2g～102g，因此集成后的MEMS陣列加速度傳感器的工作范圍為10-8g～102g，在該范圍上按照對數尺度均勻生成6×106個標定參考值，并根據三個MEMS加速度計的工作范圍為其疊加特定的隨機噪聲以生成仿真測量數據。生成仿真數據的具體過程可以表示為

(3)

式中，Di是第i個MEMS加速度計的仿真數據，M是標定參考數據，r是0～1上的均勻分布隨機數。

生成的三個MEMS加速度計的仿真數據如圖3 所示，按照對數尺度各取約9000個仿真數據進行繪制。在工作范圍內仿真測量值的相對誤差小于0.1，在工作范圍之外，其相對誤差將隨著遠離工作范圍的程度而逐漸增大。

(a) MEMS加速度計1

(b) MEMS加速度計2

(c) MEMS加速度計3圖3 三個不同工作范圍的MEMS加速度計Fig.3 Three MEMS accelerometers with different operating ranges

對三個MEMS加速度計的仿真測量數據與標定參考數據進行間隔120的等間隔采樣，構建出120個樣本容量為5000的訓練集，其中每個樣本S=(d1，d2，d3，R)由同一時刻的三個MEMS加速度計仿真測量值和標定參考值組成。

為了客觀地證明本文MEMS陣列加速度傳感器實現方法的有效性，利用最優拼接法融合三個MEMS加速度計的數據并計算其損失值作為對比。最優拼接法即在每個樣本中尋找最優的仿真測量值，因此其輸出數據精度將不低于MEMS陣列加速度傳感器中任意子傳感器的精度。最優拼接法的輸出數據損失值l的計算公式如下

(4)

仿真實驗在Python環境下搭建運行，設置最大訓練次數M=360，區間個數N=100，平滑步數K=2，調整步長α如式(5)，其中m是當前累計訓練次數。仿真實驗分為局部整定和全局整定兩個部分，在局部整定實驗中，僅對處在交疊區內進行權重自整定，而全局整定則是對所有權重進行整定。分別在120個訓練集上獨立循環運行，記錄每個訓練集的樣本平均損失，并存儲最終的權重模型。

(5)

根據記錄的各個訓練集的樣本平均損失值繪制仿真實驗的權重自整定過程曲線，如圖4所示，并采用寬度為5的滑動窗口計算樣本平均損失的滑動平均值。從局部整定過程曲線可以看出，在訓練初期樣本的平均損失下降較快，經歷約50次訓練后，提出的基于離散對數映射的自整定加權融合方法在絕大多數樣本上都能獲得低于最優拼接法的平均損失。對比局部整定過程曲線與全局整定過程曲線，可以看出后者能獲得更高的數據融合精度，因此本文的方法在非交疊區域依然能夠有效提高數據精度。

(a) 局部整定過程

(b) 全局整定過程圖4 基于離散對數映射的加權融合算法權重自整定過程Fig.4 Process of weight self-tuning of fusion algorithm based on discrete logarithm mapping

利用訓練好的權重模型在6×106個樣本上進行測試并計算平均損失，分別在三個MEMS加速度計工作范圍以陣列集成后的工作范圍上進行結果分析，分別計算四個工作范圍上仿真數據、最優拼接融合、局部整定模型和全局整定模型的平均損失，實驗結果見表1。從表1數據可以看出，本文提出的基于數據融合的MEMS陣列加速度傳感器實現方法有效地實現了三個不同范圍的MEMS加速度計的陣列集成與數據融合輸出，且構建的MEMS陣列加速度傳感器具有更高的性能，在6×106個樣本的平均損失值相比三個子傳感器最優拼接的平均損失值降低了6.1%，融合數據的精度超越了各個加速度計的原始仿真數據。

表1 仿真實驗結果及對比數據表Tab.1 Table of simulation experiment results and comparative data

4 結 論

本文針對單MEMS加速度計性能有限無法滿足實際工程中日益復雜且嚴苛的檢測需求的問題，提出了一種基于數據融合的MEMS陣列加速度傳感器實現方法，在仿真環境下，實現了陣列集成三個不同范圍的MEMS加速度計以提高檢測性能的目的，相比于最優拼接法的平均損失降低了6.1%，且融合數據的精度超越了各個加速度計的原始仿真數據。但本文未能完全還原真實MEMS加速度計的數據特性，后續將搭建MEMS陣列加速度計樣機并進行功能驗證與優化，使其應用于實際工程中的寬頻振動信號檢測任務。