類蛛網狀盤式諧振微陀螺的抗沖擊性能與結構誤差仿真分析*

樊 波，郭述文

(1.南華大學 電氣工程學院·衡陽·421001；2.蘇州大學 微納傳感技術研究中心·蘇州·251001；3.華東光電集成器件研究所·蚌埠·233040)

0 引 言

基于微納加工技術的微機械陀螺因尺寸小、成本低、功耗低，以及易于與信號處理電路集成等優勢，目前已經占據了大部分消費類電子、汽車電子、工業控制、安全檢測等中低端應用場景[1]。為了拓展高端應用場景市場，具有中心對稱、低錨定損耗、大模態質量和免疫外部振動等特點的盤式諧振微陀螺成為近年來微機械陀螺主流的研究方向[2]。

目前國內外主要采用兩種方案設計高性能盤式諧振微陀螺。一種方案為通過結構參數優化實現，斯坦福大學通過有限元仿真分析了環寬、環數、輻條角度、輻條寬度等結構參數對諧振頻率和品質因數的影響，并通過分析結果優化了盤式諧振微陀螺性能[3]；國防科技大學通過采用粒子群算法對環寬和輻條長度等結構參數進行優化，改進了陀螺的品質因數、機械靈敏度和機械熱噪聲等性能參數[4-5]。另一種方案主要為優化陀螺敏感結構，加州大學歐文分校提出了外錨點內電極的盤式諧振微陀螺，工作在模態階數n=3的酒杯模態，具有極佳的標度因子穩定性[6]；斯坦福大學提出在盤式諧振微陀螺環與環之間設置雙電極的方案，大幅度增加了電容傳感面積[7]；美國ADI公司提出了復合環內外雙錨點的盤式諧振微陀螺，能有效提高角增益[8]；國防科技大學提出了懸掛質量塊的優化方案和蜂窩狀盤式諧振微陀螺，能有效提高品質因數和制作誤差對結構頻率裂解的魯棒性[9-10]。本研究小組近年來利用直線形結構工藝誤差小于弧形結構的工藝特點提出了一種全線性結構的類蛛網狀盤式諧振微陀螺，并結合懸掛質量塊，可有效提高品質因數和減少工藝誤差[11]。

為了解類蛛網狀盤式諧振微陀螺的結構特性、抗沖擊性能和非理想情況工作頻率特性，則需要建立準確的理論模型。因此本文采用有限元軟件進行模態分析和過載分析，并開展結構誤差的頻率裂解仿真研究。

1 結構介紹及其工作原理

類蛛網狀盤式諧振微陀螺由10個同心的正十六邊形環組成，通過八個輻條交替連接到中心錨點。每個環由16個相同的矩形梁端到端連接。小實心質量塊被懸掛在從內到外的奇數層環和偶數輻條層。相鄰的正十六邊形諧振環與輻條之間形成凹槽，所述凹槽內設置有雙層電極，目的是增加驅動和檢測的傳導面積以及頻率調諧能力。正多邊形結構全部采用直線連接，諧振器近似多環圓盤結構，實為全線形結構，沒有圓弧線。因此，邊緣誤差效應小，對稱性誤差相對較小，2個工作模態諧振頻率裂解小[12]。其結構如圖1所示。

圖1 類蛛網狀盤式諧振微陀螺敏感結構示意圖Fig.1 Structural schematic of micro cobweb-like disk resonator gyroscope

該結構為軸對稱陀螺敏感結構，工作振動模式為具有一對平面內橢圓彎曲的振動模式，驅動模態和敏感模態的波腹角相差45°，但相位差為90°，這種振型也被稱為四波腹振型，即n=2酒杯模態振型，其工作振型如圖2所示。這意味著當陀螺敏感結構在0°方向產生恒幅振動時，有Z軸角速度輸入，會在45°方向上產生位移。

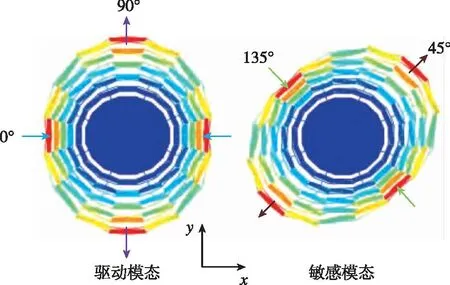
圖2 類蛛網狀盤式諧振微陀螺n=2酒杯振型Fig.2 n=2 wineglass mode shape of micro cobweb-like disk resonator gyroscope

2 結構特性仿真分析

陀螺芯片的結構形狀和結構參數決定了諧振模態、抗沖擊等結構特性，陀螺芯片采用(111)單晶硅材料，經過絕緣體上硅(Silicon-on-Insulator，SOI)工藝加工制作而成，其結構參數和主要材料屬性分別如表1和表2所示，通過模態分析和沖擊分析得到諧振頻率、最小寄生模態頻差(即寄生模態與工作模態之間最小頻差)和最大沖擊載荷加速度等性能參數。

表1 類蛛網狀盤式諧振微陀螺敏感結構參數Tab.1 Structure parameters of micro cobweb-like disk resonator gyroscope

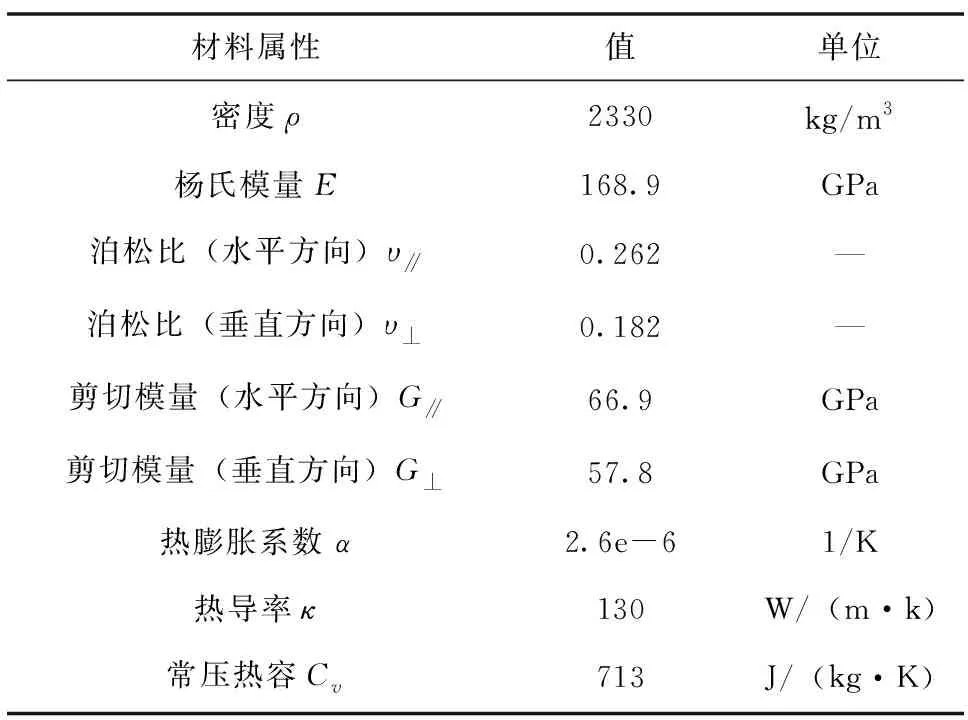
表2 常溫(T=298.15K)下(111)單晶硅材料屬性Tab.2 Properties of (111) single crystal silicon at room temperature (T=298.15K)

2.1 模態分析

對于類蛛網狀盤式諧振微陀螺而言，確定諧振器工作模態諧振頻率以及寄生模態頻差對陀螺性能極為重要。其中諧振頻率是諧振器性能指標的重要參數，寄生模態頻差過小可能會降低品質因數和引入混模干擾，甚至導致陀螺無法正常工作。因此需采用模態分析研究陀螺敏感結構的固有頻率和模態振型等特性。本文在不考慮結構誤差的情況下，采用有限元軟件對陀螺進行模態分析，提取并分析了前10階模態的頻率和振型。

在有限元分析軟件中，模態分析是利用系統固有的模態的正交性，建立用模態坐標和模態參數所描述的模態方程，并通過模態疊加法對其進行求解，并基于以下3個假設：

1)載荷具有時不變性；

2)剛度和質量矩陣為常量；

《指路經》在西南少數民族的葬禮中比較普遍。苗族的《指路經》，內容從死者出生開始說起，講到他（她）出生的地方（也是埋衣胞的地方），他（她）為什么死，他（她）離開家如何去到祖先亡靈所在的地方，路上如何應答，如何過河，如何辨認誰是祖先，等等。

3)在未使用阻尼特征求解法情況下，不考慮阻尼效應。

通過參數化建模，設置材料屬性和邊界條件，以及采用網格劃分后，再利用特征頻率法對諧振器進行求解，計算得前10階模態頻率和模態振型分布，如表3和圖3所示。

表3 類蛛網狀盤式諧振微陀螺前10階模態諧振頻率Tab.3 First 10 order modal resonance frequency of micro cobweb-like disk resonator gyroscope

(a) 第1階 面外翹曲振動模態(0°方向) (b) 第2階 面外翹曲振動模態(45°方向)

(c) 第3階 面外搖擺振動模態(0°方向) (d) 第4階 面外搖擺振動模態(90°方向)

(e) 第5階 X軸擺式振動模態 (f) 第6階 Y軸擺式振動模態

(g) 第7階 n=2階酒杯式振動模態(0°方向) (h) 第8階 n=2階酒杯式振動模態(45°方向)

其中，第1、2階模態沿Z軸方向彎曲振動，互成45°方向、面外翹曲振動模態(圖3(a)、(b))，諧振頻率約為8.7kHz。第3、4階模態沿Z軸方向上下搖擺，互成90°方向、面外搖擺振動模態(圖3(c)、(d))，頻率約為11.1kHz。第5、6階模態分別在XY平面內沿X軸左右搖擺和沿Y軸前后搖擺，為X軸擺式振動模態和Y軸擺式振動模態(圖3(e)、(f))，頻率約為14.9kHz。第7、8階模態在XY平面內互成45°角兩個方向的橢圓彎曲振動(四波腹振動)，且兩個模態的波節點和波腹點互為相反對應關系，即n=2酒杯式振動模態(圖3(g)、(h))，兩模態諧振頻率約為18.8kHz。第9、10階模態在XY平面內互成30°角兩個方向的三葉草式振動，為n=3酒杯式振動模態(圖3(i)、(j))，頻率約為23.6kHz。其中第7階和第8階模態為工作模態，其與前后相鄰寄生模態頻率的頻差約為3.9kHz和4.8kHz，較大的頻差可有效避免模態間的耦合。同時，兩工作模態諧振頻率在設計時完全匹配，可實現機械靈敏度最大，且機械熱噪聲最小。依據仿真結果，陀螺諧振器的結構參數滿足模態匹配設計的原則，且能有效抑制寄生模態耦合效應。

2.2 沖擊分析

MEMS陀螺從實驗室到工程化轉換階段，抗沖擊能力是其重點考慮的問題之一。機械沖擊定義為短時間施加于機械系統或其一部分的劇烈且非周期性的載荷作用，常見有半正弦脈沖、梯形脈沖等[13]。沖擊仿真分析采用有限元軟件的瞬態響應分析方法，研究MEMS陀螺敏感結構在強瞬態沖擊載荷下的應力分布。

在MEMS陀螺中，最常見的沖擊失效現象是斷裂。根據Von Mises屈服準則，當最大應力畸變能密度大于或者等于材料單向拉伸屈服時的畸變能密度時，結構會發生斷裂。晶體硅為一種純脆性材料，為了盡量減少在給定的沖擊水平下斷裂的可能性，其中一個設計標準是保持最大Von Mises應力低于1GPa[14]。

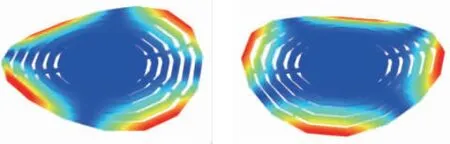
為模擬沖擊環境下的過載特性，通過有限元軟件在X、Y、Z三軸方向上對陀螺敏感結構施加脈寬為2ms的半正弦沖擊載荷，選擇幅值分別為15000g、20000g、25000g和30000g(g=9.98m/s2，為重力加速度)，分析該結構在沖擊載荷下的瞬態響應，明確其抗動態沖擊過載能力。圖4(a)和(b)分別為MEMS陀螺在X(Y)軸和Z軸沖擊載荷下其敏感結構最大Von Mises應力的時間響應曲線。顯然，在相同載荷下，由于結構完全對稱，在平面內X軸和Y軸方向所受的最大Von Mises應力基本一致，而在Z軸方向小于平面內X軸和Y軸方向所受最大Von Mises應力。這是由于Z軸方向擺式振動模態的諧振頻率高于平面內擺式振動模態，也說明諧振器在Z軸方向可承受更大的加速度沖擊載荷。陀螺敏感結構在X軸方向25000g的加速度沖擊載荷下最大Von Mises應力為974.6MPa，而在30000g的沖擊載荷下最大Von Mises應力為1169.5MPa。根據設計標準，陀螺敏感結構可承受25000g的加速度沖擊載荷。這表明該結構的抗沖擊性好，可承受高加速度沖擊載荷而無需任何特殊保護。

(a) X(Y)軸方向沖擊載荷

(b) Z軸方向沖擊載荷圖4 沖擊載荷下陀螺動態響應曲線Fig.4 Dynamic response curves of the gyroscope under impact load

一般不同的應用環境產生的沖擊強度不一致。常見的應用環境要求能夠承受7000g以下的沖擊強度。如汽車應用中，要求安全氣囊傳感器在20～50g的沖擊環境下工作，爆震傳感器需在1000g的沖擊環境下工作。其他汽車應用要求設備能承受3000g的沖擊強度[15]。在惡劣的環境中，則需要承受更高的沖擊強度，通常為10000g以上。如油氣勘探中傳感器需要承受20000g的沖擊力；在軍事應用中，制導導彈的炮彈發射往往需要承受高沖擊，過載加速度載荷可達15000g以上[16]。根據沖擊分析結果，類蛛網狀盤式諧振微陀螺適用于所有常見的應用環境，甚至部分惡劣環境。

3 結構誤差分析

(a) (b)

(c) (d)圖5 SEM圖：CDRG的整體結構圖(a)和局部放大圖(b)，以及RDRG的整體結構圖(c)和局部放大圖(d)Fig.5 SEM photos：a fabricated CDRG：overview (a) and magnified view (b)；a fabricated RDRG：overview (c) and magnified view (d)

3.1 晶向誤差

研究(111)單晶硅晶向誤差對頻率裂解的影響，首先需確定晶向誤差來源。對于SOI晶圓，有兩種常見的公差規范：晶圓平面(Wafer-flat，晶圓的頂部表面)切割對準失配和晶圓主平面定位誤差[17]。根據制造商提供的規范，本研究使用的晶圓切割對準誤差為[111]晶向0.2°，晶圓定位誤差為[110]晶向0.5°。

為確定晶向誤差對頻率裂解的影響，首先要通過線性本構方程找到晶向誤差對應的剛度矩陣。由于單晶硅的單位單元是面心立方晶格，因此，(100)單晶硅相對于固定笛卡爾坐標系的剛度矩陣為[18]

(1)

其中彈性常數的值給出如下[18]

C11=165.7GPa,C12=63.9GPa,
C44=79.6GPa

(2)

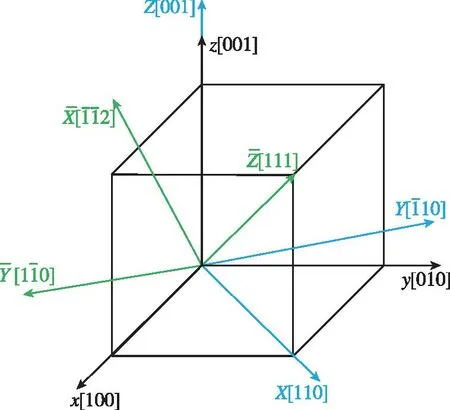
(a) 兩種晶圓的坐標系配置

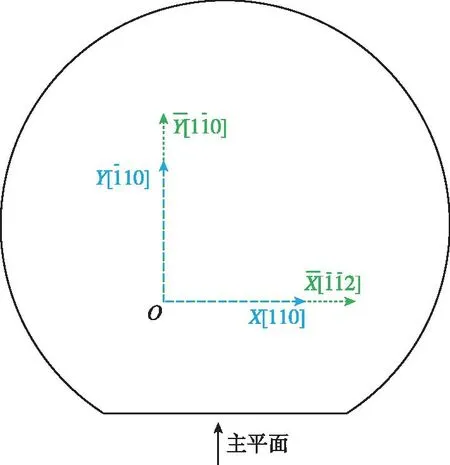
(b) 兩種晶圓的頂視圖圖6 (100)和(111)單晶硅晶圓的坐標系統和頂視圖Fig.6 Coordinate systems and overhead views of the (100) and (111) single crystal silicon wafers

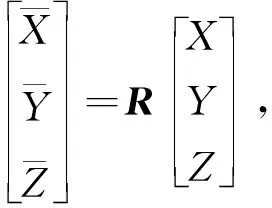
(3)

(4)

(5)

其中，

(6)

σ′=Mσ

(7)

其中，

M=

ε′=Nε

(8)

其中，

N=

C′=MCN-1

(9)

取不同的θ值，得到不同的剛度矩陣C′。采用上述分析方法也可獲得晶圓切割失配誤差對應的剛度矩陣C′，均可通過Matlab編寫代碼求解得到所需剛度矩陣。將剛度矩陣代入有限元分析軟件中，仿真計算得到[110]和[111]晶向偏轉角度情況下的頻率失配，仿真結果如圖7所示[11]，其中紅色直線和藍色直線分別表示RDRG和CDRG的頻率裂解與晶向誤差的關系。

圖7 由晶向誤差引起的 CDRG和RDRG頻率裂解仿真結果Fig.7 Simulation results of CDRG and RDRG frequency splitting caused by crystal orientation error

仿真結果表明，沿[111]晶向(Z軸)的角度偏轉對頻率裂解沒有影響，如圖7中虛線所示。這是由于對于(111)單晶硅，楊氏模量、泊松比和剪切模量是水平方向和垂直方向各向同性的[18]，垂直方向的偏角對水平方向振動模態的諧振頻率沒有影響。圖7還描述了兩種結構在[110]晶向上的定位誤差與頻率裂解的關系。顯然RDRG頻率裂解的晶向誤差敏感度為23.18Hz/(°)，而CDRG為16.8Hz/(°)；CDRG頻率裂解的晶向誤差敏感度相較于RDRG降低了27.53%，說明類蛛網狀盤式諧振微陀螺頻率裂解對晶向誤差的敏感度更低。

3.2 工藝誤差

在加工過程中，掩模版的精度限制、光刻縮放，以及DRIE刻蝕工藝的lag效應和刻蝕速率非均勻等都會影響陀螺敏感結構成品的對稱性，造成頻率失配。其中由DRIE刻蝕引起的環寬非均勻是造成頻率分裂的重要原因[21]，故需要通過仿真環寬非均勻性來表征工藝誤差對頻率裂解的影響。實際加工過程中形成的環寬非均勻具有隨機性，有限元分析軟件難以模擬，可將其等效為在均勻環上某一方向上增加或者減少環寬。本文通過有限元分析軟件建立理想模型，并在圓環狀盤式諧振陀螺模型每個環的0°方向上附加圓弧角為22.5°的弧形梁，以及對類蛛網狀盤式諧振陀螺模型每個環的0°方向上附加等角的直梁來模擬環寬非均勻 (見圖8(a))[11]，其中附加梁寬為ΔW，用以表征工藝誤差，均勻環寬為W0。

(a) 環寬非均勻等效模型

(b) 仿真結果圖8 工藝誤差對CDRG和RDRG頻率裂解的仿真結果Fig.8 Simulation results of process error on frequency splitting of CDRG and RDRG

為分析ΔW對頻率裂解的影響，采用有限元軟件對ΔW進行參數化仿真，設置范圍為0～1μm，間隔為0.1μm，應用固體力學模塊，采用特征頻率法求解諧振頻率，得到兩種結構頻率裂解與ΔW的關系，如圖8(b)所示[11]。從圖中可知，CDRG和RDRG的頻率裂解對應斜率分別為76.7Hz/μm和84.8Hz/μm。CDRG的環寬非均勻誤差敏感度相較于圓環狀盤式諧振陀螺降低了9.55%，說明類蛛網狀盤式諧振微陀螺對工藝誤差的魯棒性更高。

綜上所述，由仿真分析結果可以看出，類蛛網狀盤式諧振陀螺對結構誤差的敏感度低于圓環狀盤式諧振陀螺，可見類蛛網狀盤式諧振陀螺具有更佳的結構誤差魯棒性。

4 結 論

本文通過有限元軟件對類蛛網狀盤式諧振微陀螺的模態頻率、抗沖擊等結構特性進行了研究，并進行了結構誤差對頻率裂解影響的仿真分析。仿真結果表明，類蛛網狀盤式諧振微陀螺具有抗高過載的優異性能，且對結構誤差的魯棒性優于圓環狀盤式諧振陀螺。這說明該結構具有高性能潛力且可應用于惡劣環境。