關于函數極值問題的注記

呂偉

山東省菏澤市鄆城縣黃泥岡鎮初級中學 山東鄆城 274700

極值理論是高等數學函數理論中的重要內容，函數極值反映了函數形態的一個重要特性。極值問題一直是數學理論中研究函數問題的重要內容之一，在科學和生產實踐中存在著許多和極值有關的問題。比如在工農業生產、自然科學、工程技術和經濟發展這類問題中出現的最大產量、最大收益、最小成本、最大利潤等一系列問題，其實質都是函數極值問題，都可以利用極值理論和方法予以解決。因此，極值理論不僅具有抽象的理論意義，也是解決實際問題的重要方法和手段。

在教學過程中我們發現，很多學生對極值點的種類、極值(點)與最值(點)的關系等問題會產生疑惑，并且很多高等數學或微積分教材中對這類問題也沒有進行有針對性的分析、講解。一些相關專家、學者從不同角度對這類問題進行了探討[1-12，14-16]，本文針對在教學、學習極值理論過程中出現的上述問題進行進一步的探討，以期為今后的教學和學習提供幫助和參考。

極值問題和極值理論通常可分為一元函數和多元函數兩種情形。我們主要以一元函數為例進行探討，相關結論也相應地被推廣到了多元函數的情形。

1 函數極值的性質

首先，我們要明確極值、最值及相關概念。本文中，我們以I表示數軸上的某一區間。

定義1.1[13]設R為實數集合，x0∈R，δ>0均為實數，稱開區間(x0-δ，x0+δ)為點x0的δ鄰域，記作U(x0，δ)。x0稱為該鄰域的中心，δ稱為該鄰域的半徑。

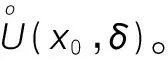
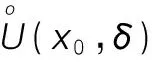
定義1.4 設函數f(x)在I上有定義，x0是I上一點。若對任意的x∈I，有f(x)≤f(x0)(或f(x)≥f(x0))，則稱f(x0)是f(x)在I上的最大值(或最小值)，x0稱為f(x)在I上的最大(小)值點。最大值與最小值統稱為最值，最大值點與最小值點統稱為最值點。

由上述關于極值與最值的定義，我們可以得到函數f(x)在I上的極值與最值具有如下性質。

注記1.1 (1)極值是一個局部概念，最值是一個全局性概念。也就是說，極值是函數在一點的某一小鄰域內的最大值或最小值，但最值是函數在區間I上的最大值或最小值。

(2)極值只能在區間I的內部取到，但最值可能在I的內部取到，也可能在I的邊界點處取得，除非I是不包含邊界點的開區間。這是因為，I的邊界點不存在以其為中心的鄰域，由定義1.3知，函數在I的邊界點沒有極值。

(3)極值在區間I上可能是不唯一的，但最值在I上若存在必是唯一的。

2 函數極值點的種類

首先給出駐點的定義和極值的必要條件。

定義2.1[13]設函數f(x)在點x0的某鄰域U(x0，δ)內有定義，且在x0處可導，若f′(x0)=0，則稱x0為f(x)的駐點。

引理2.1[13]設函數f(x)在點x0處可導，且在x0處取得極值，則f′(x0)=0。

引理2.1告訴我們，可導函數f(x)的極值點必是其駐點，但函數的駐點卻未必是其極值點，具體例子見下面的例2.1。

另外，函數也可能在不可導的點處取得極值，具體例子見下面的例2.2。

下面我們再給出判斷函數在駐點和不可導點取得極值的一個充分條件。

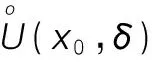
(1)若x∈(x0-δ，x0)時，f′(x)>0，而x∈(x0，x0+δ)時，f′(x)<0，則f(x)在x0處取得極大值；

(2)若x∈(x0-δ，x0)時，f′(x)<0，而x∈(x0，x0+δ)時，f′(x)>0，則f(x)在x0處取得極小值；

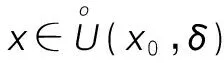
該充分條件說明，若導數f′(x)在鄰近點x0的左、右兩邊符號不同，則f(x0)是極值，否則不是極值。

例2.1 設函數f(x)=ex3-1的駐點，并判斷f(x)的駐點是否為極值點。

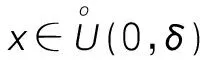
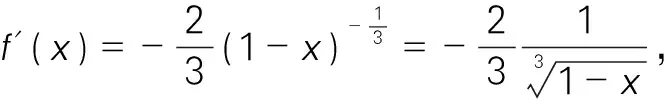
由以上的討論我們可以得到關于一元函數極值點的如下性質。

注記2.1 函數f(x)在區間I上的極值點包括兩類點：駐點和不可導的點，但這兩類點未必都是極值點。

3 函數最值點的種類及其與極值點的關系

由極值與最值的定義及注記1.1、注記2.1，我們可以得到關于一元函數f(x)在區間I上的極值與最值的如下性質。

注記3.1f(x)的最值若在I的內部取到，則其一定也是相應的極值；f(x)的最值若在I的邊界點處取到，則其不是極值。反之，區間I上的極值可能是最值，也可能不是最值。

注記3.2f(x)在I上的最值點與極值點的關系如下：

我們以一個具體的例子來說明上述兩個結論。

例3.1 已知函數:

試求f(x)在區間I=[-2，4)上的極值與最值。

解 由f(x)的表達式，可得:

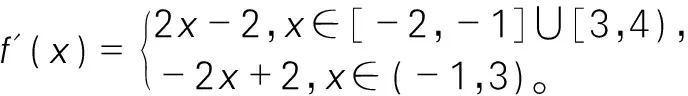
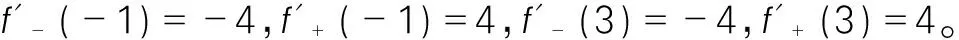
利用引理2.2容易判斷，x1=1是極大值點，x2=-1是極小值點，x3=3是極小值點。且f(-2)=5，f(-1)=0，f(1)=4，f(3)=0。故f(x)在區間[-2，4)上的極小值為f(-1)=f(3)=0；極大值為f(1)=4；最大值為f(-2)=5；最小值為f(-1)=f(3)=0。

4 多元函數極值問題的情形

在這部分內容里，我們以二元函數為例說明在學習和處理多元函數極值問題時應注意的問題。首先我們給出平面(R2)上一點鄰域的概念。

定義4.1[13]設P0(x0，y0)是xoy平面上一點，δ是某一正數，與點P0(x0，y0)距離小于δ的點P(x，y)的全體，稱為點P0的δ鄰域，記作U(P0，δ)，即:

U(P0，δ)={P||PP0|<δ}

其中，P0(x0，y0)稱為該鄰域的中心，δ稱為該鄰域的半徑。

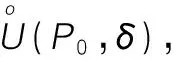
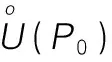
由鄰域的定義我們知道，平面上點P0的δ鄰域是以點P0為中心，以長度δ為半徑的開圓面，它實際上是一維情形中的開區間的推廣。

在鄰域這一概念的基礎上，我們再給出在討論多元函數問題時常用到的概念，即區域。

定義4.2[13]設P是平面R2上任意一點，E∈R2是平面上任意一點集。如果存在點P的某個鄰域U(P)，使得U(P)?E，則稱點P為E的內點。

定義4.3[13]如果點集E的點都是E的內點，那么稱E為開集。

定義4.4[13]如果點集E內任何兩點，都可以用折線連接起來，并且該折線上的點都屬于E，那么稱E為連通集。

定義4.5[13]連通的開集稱為區域或開區域。

定義4.6[13]開區域連同它的邊界一起所構成的點集稱為閉區域。

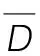
利用鄰域和區域的概念，可以把一元函數極值與最值的概念推廣到多元函數的情形，這里我們不再贅述這些概念，有需要的讀者可參閱文獻[13]等相關資料。

下面我們給出二元函數極值的必要條件和充分條件。

引理4.1[13](必要條件)設函數z=f(x，y)在點(x0，y0)具有偏導數，且在點(x0，y0)處有極值，則有fx(x0，y0)=0，fy(x0，y0)=0。

我們稱使fx(x，y)=0，fy(x，y)=0，同時成立的點(x0，y0)為函數f(x，y)的駐點。

引理4.2[13](充分條件)設函數z=f(x，y)在點(x0，y0)的某鄰域內連續且有一階和二階連續偏導數，又fx(x，y)=0，fy(x，y)=0，記fxx(x0，y0)=A，fxy(x0，y0)=B，fyy(x0，y0)=C，則有如下結論成立：

(1)當AC-B2>0時，函數f(x，y)在點(x0，y0)處取得極值。且當A<0時取極大值；當A>0時取極小值。

(2)當AC-B2<0時，函數f(x，y)在點(x0，y0)處不取極值。

(3)當AC-B2=0時，無法判斷函數f(x，y)是否在點(x0，y0)極值，需要利用其他方法來判斷。

顯然，引理4.2只能用來判斷二元函數是否在其駐點處取得極值。

仿照一元函數的情形，我們可以得到關于二元函數極值和最值的如下性質。

注記4.1 函數z=f(x，y)在區域D上的極值點包括兩類點：駐點和不可導的點，但這兩類點未必都是極值點。

注記4.2 針對引理4.2中的第三種情形和偏導數不存在的點，我們可以利用極值的定義來判斷。

我們利用下面的例題說明注記4.2。

例4.1 設函數f(x，y)=x2+y2-2xy，試判斷駐點是否為函數的極值點。

解 由已知，fx(x，y)=2x-2y，fy(x，y)=2y-2x。故該函數的駐點為直線y=x上的任意點(x，x)。又沿直線y=x上的點A=fxx(x，y)=2，B=fxy(x，y)=-2，C=fyy(x，y)=2。

這樣，AC-B2=0，引理4.2無法判斷該函數的駐點是否為極值點。但我們可以把函數整理為f(x，y)=(x-y)2，顯然對y=x上的點(x，y)=(x，x)的任一鄰域內的其他點(x，y)(x≠y)，都有f(x，y)=(x-y)2>f(x，x)=0。因此，按照極值的定義知道，該函數的駐點是其極大值點，極大值為0。

因此，按照極值的定義，函數在(0，0)處取得極小值。

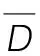
對多元函數極值的其他性質，可以仿照注記1.1和注記3.1給出，我們在此也不再贅述。