一種分區快速航跡關聯算法

莊 俊，楊 沛

(解放軍63889部隊，河南 孟州 454750)

0 引 言

分布式多傳感器信息融合系統中，為解決目標重復跟蹤問題，需要建立來自不同傳感器的局部航跡之間的對應關系，即進行航跡關聯[1]。航跡關聯是多傳感器系統后續進行融合、識別處理的依據。

分布式多傳感器系統的傳感器一般配置在很寬廣的地理范圍上，所以系統目標區域較大[2]。如果直接對整個目標區域的所有局部航跡進行兩兩航跡關聯，運算量會非常大，難以滿足工程應用的實時計算要求。所以，選擇一種能夠降低航跡關聯運算量的方法是必要的。

近年來，有一些文獻對如何降低航跡關聯運算量這一問題進行了研究。文獻[3]利用剖分的網格對目標進行分配，減少了目標之間進行兩兩關聯的次數，從而降低了運算量；文獻[4]提出了將目標進行分區，只對本區域和相鄰區域進行航跡關聯的策略，但該策略仍有較多重復計算；文獻[5]基于網格技術將關聯計算分解成多個小任務，各個小任務并行計算，這種方法受處理器并行性能的影響，并未從根本上降低運算量。

本文提出了一種分區快速航跡關聯算法，該算法將目標區域劃分為若干個子區域，對目標區域內的航跡進行分區，只對同一子區域內的航跡進行兩兩關聯判決。為了抑制分區導致的漏關聯和錯關聯，相鄰子區域間設置重疊區域。隨著目標區域內航跡密度變化，自適應選擇最優分區數。仿真實驗表明，該算法可有效降低航跡關聯的運算量。

1 航跡關聯算法概述

目前，常用的航跡關聯算法可分為3類：第1類是基于統計理論的航跡關聯算法，主要有加權法[6]、修正法[7]、最近鄰域法、經典分配法等；第2類是基于模糊理論的關聯算法，主要有模糊雙門限法[8]、模糊綜合決策法[9]等；第3類是基于灰色理論[10]的關聯算法。基于統計理論的航跡關聯算法在目標密集、存在較多航跡交叉、分岔及傳感器存在較大誤差場景下關聯性能嚴重降低；基于模糊理論的航跡關聯算法在上述場景下的關聯性能優于基于統計理論的關聯方法，但其參數設置復雜，需要通過大量的仿真確定；基于灰色理論的航跡關聯算法對傳感器數據的要求較少，參數設置較少，比較適合于工程應用。本文算法仿真選擇灰關聯算法進行航跡關聯。

2 基于區域劃分的航跡關聯

本文對航跡關聯算法的研究是基于兩坐標雷達進行的，很容易推廣到三坐標雷達的應用。

2.1 目標區域劃分方法

傳統航跡關聯算法在進行精關聯之前，一般要先設定關聯門限進行粗關聯，大于粗關聯門限的航跡點之間是沒有必要進行關聯比較的。所以，可以考慮將目標區域劃分成若干個小區域，只對小區域范圍內的目標航跡點進行關聯，從而減少兩兩航跡關聯次數，降低航跡關聯運算量。

將多傳感器系統目標區域按照一定策略劃分后的小區域稱為目標子區域，目標子區域可以根據需要繼續劃分成更小的目標子區域。

由于自身精度的影響和各種雜波及干擾的存在，傳感器的量測數據或多或少會存在一定的系統誤差和隨機誤差，目標航跡會偏離目標真實位置，進行區域劃分時有可能將不同傳感器源于同一目標的航跡劃分到不同目標子區域，從而產生漏關聯或錯關聯。為了抑制分區導致的漏關聯和錯關聯，在相鄰目標子區域之間設置部分重疊區域。如圖1所示，假設目標區域為一長方形區域，將目標區域平均劃分為若干個目標子區域，Δx、Δy為目標子區域長度和寬度，灰色區域為相鄰目標子區域之間的重疊區域，寬度為D。

圖1 目標區域劃分示意圖

2.2 重疊區域寬度計算

以兩坐標雷達為例，傳感器對目標的量測是在極坐標系下獲取的，其距離和方位測量誤差分別為σr、σa，為了計算方便，需要將雷達在距離和方位上的測量誤差變換到直角坐標系中，分別為σx、σy，其計算公式為：

(1)

式中:R為距離量測值；A為方位量測值。

設傳感器1的最大作用距離為Rmax1，則可根據式(1)計算出傳感器1對目標的最大測量距離偏差為Δdmax1。假設多傳感器系統中共有S個主動傳感器，則系統中傳感器對目標的量測距目標真實位置的最大距離偏差為：

Δdmax=maxΔdmaxs,s=1,2,…,S

(2)

2個傳感器對同一目標的量測距離偏差可能方向相反，則2個傳感器對同一目標的量測之間的距離最大為Δdmax的2倍。所以，重疊區域寬度D應大于系統最大距離偏差的2倍。同時，為了避免重疊區域過大，增加重復關聯運算量，按照重疊區域不大于目標子區域面積一半的原則，重疊區域寬度D應小于min(Δx、Δy)的一半。

2.3 關聯沖突處理

由于相鄰目標子區域之間存在重疊區域，處于重疊區域內的航跡可能同時和2個或2個以上航跡點關聯成功。假設傳感器1的航跡i在l時刻的航跡點處于目標子區域的重疊區域，在l時刻分區航跡關聯結果中傳感器1的航跡i同時和傳感器2的航跡j和k關聯成功，如圖2所示，則航跡關聯對t1_i、t2_j和航跡關聯對t1_i、t2_k沖突。

關聯沖突處理機制如下：比較航跡i與j之間的距離dij和航跡i與k之間的距離dik，若dij>dik，則判定航跡i與k關聯成功；否則，判定航跡i與j關聯成功。

3 最優分區數確定

與一般航跡關聯算法不同的是，分區航跡關聯算法在進行航跡關聯之前，需要先對輸入航跡進行子區域劃分，將各子區域航跡進行獨立存儲，然后分別對各子區域航跡進行關聯，最后對各子區域關聯關系表進行合并和關聯沖突處理，形成關聯關系總表。因此，為了評估分區航跡關聯算法的運算量，需要綜合評估目標子區域劃分和子區域航跡關聯的運算量。

假設2個傳感器目標區域完全重疊，目標區域內航跡總數為N，將目標區域劃分為M個目標子區域。對目標子區域劃分和航跡關聯的時間復雜度進行分析，進而對最優分區數進行判定。

3.1 目標子區域劃分復雜度分析

對輸入航跡進行子區域劃分時，目標子區域數M越大，搜索某航跡所屬子區域的運算量就越大，存儲子區域航跡數據的數據結構也越復雜，運算時間復雜度隨M線性變化；航跡數N越大，子區域劃分的運算量也越大，運算時間復雜度隨N線性變化，則目標子區域劃分對M和N的時間復雜度均為O(n)。

3.2 目標子區域航跡關聯算法復雜度分析

假設某時刻落入目標子區域i(i=1,2,…,M)內的航跡數為Ni，則目標子區域i內的航跡關聯次數為Ni2，整個目標區域內的航跡關聯總次數為∑Ni2。若不對目標區域進行分區，則航跡關聯次數為N2。不考慮目標航跡落入相鄰目標子區域之間重疊區域的情況，則有:

特別地，當航跡均勻分布在各目標子區域，即Ni=N/M時，則：

(4)

由式(3)和式(4)可以看出，子區域航跡關聯運算量隨航跡數N變化的時間復雜度為O(n2)，隨子區域數M變化的時間復雜度為O(1/n)。

3.3 最優分區數判定

分區航跡關聯算法耗時為子區域劃分耗時和子區域航跡關聯耗時之和。當航跡數N不變時，隨著子區域數M的增加，子區域劃分耗時線性增加，而子區域航跡關聯耗時線性減少，則可能存在1個拐點(最小值)，使得在該分區數下分區關聯算法總耗時最小。影響算法總耗時隨M變化的趨勢的因素主要有子區域劃分方法和航跡關聯算法。

由于子區域劃分運算量隨航跡數N變化的時間復雜度為O(n)，子區域航跡關聯運算量隨航跡數N變化的時間復雜度為O(n2)，則隨航跡數N的變化，耗時最少的最優分區數也可能發生變化。

工程應用中，可在航跡關聯系統調試時運用仿真數據對系統進行測試，得到在不同目標密度下的最優分區數。實際應用中，根據輸入的航跡數量自動調整目標子區域數，使系統關聯耗時最少，提高了系統效率。

4 算法仿真與分析

4.1 仿真場景設置

假設目標在二維平面運動，各目標起始方位和航向在[0,2π]內服從均勻分布，距離在[5 km,40 km]內服從均勻分布，速度在[100 m/s,300 m/s]區間服從均勻分布，過程噪聲協方差Q=diag[100,100]。2部雷達均位于坐標原點，雷達1的測距標準差e1r=50 m，測角標準差e1θ=0.1°，測距系統誤差Δ1r=20 m，測角系統誤差Δ1θ=0.1°；雷達2的測距標準差e1r=50 m，測角標準差e1θ=0.1°，測距系統誤差Δ1r=100 m，測角系統誤差Δ1θ=0.2°。采樣周期T=1 s，仿真時長50 s，蒙特卡洛仿真50次。目標區域內目標個數分別為50、100、200、400，將整個目標區域按橫、縱坐標劃分為1、4、9、16、25、36、49、64、81、100個目標區域，相鄰區域間重疊區域寬度為1 km。選用灰關聯算法進行航跡關聯[12]，統計不同目標密度下不同分區數時的關聯性能和運算耗時。

4.2 仿真結果分析

對不同目標密度不同分區數下子區域劃分和航跡關聯耗時進行統計，結果見表1～表3，圖3～圖4為對應的時間統計曲線。

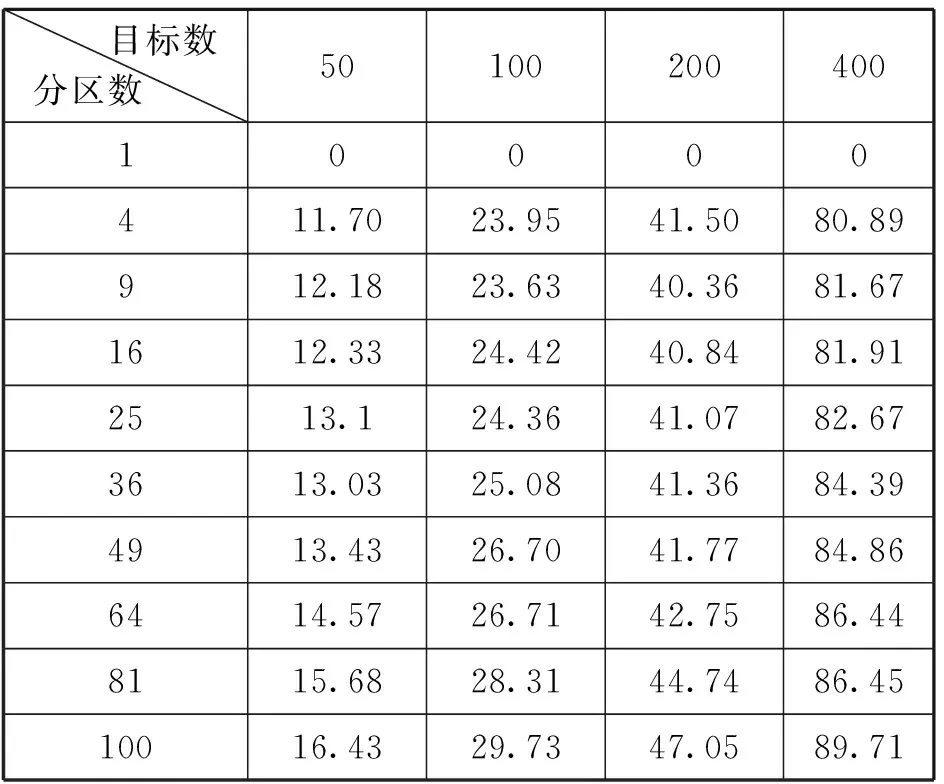
表1 子區域劃分耗時(單位：s)

表2 子區域航跡關聯耗時(單位：s)

表3 航跡關聯總耗時(單位：s)

由表1和圖3可以看出，子區域劃分耗時隨航跡數N和子區域數M的增加線性增加。由表2和圖4可以看出，子區域航跡關聯耗時隨航跡數N的增加呈平方階增加，但隨子區域數M的增加并不是線性減少的。這是由于重疊區域的存在，使得分區數較大時，重復關聯運算量也比較大，增加了關聯耗時。

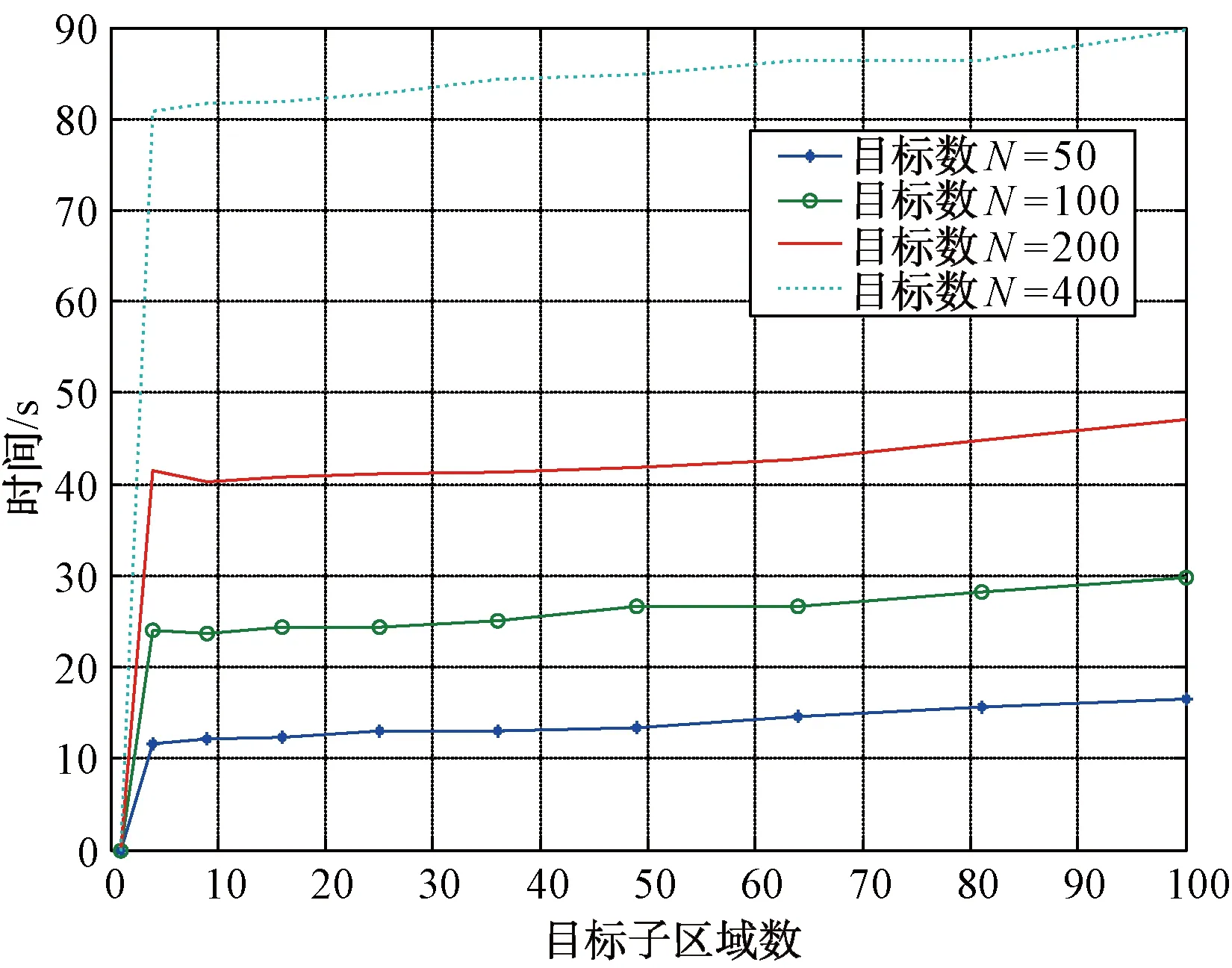
圖3 子區域劃分耗時

圖4 子區域航跡關聯耗時

由表3和圖5的統計結果可以看出，對目標區域進行分區，能夠大大降低運算量，提高了關聯速度。子區域劃分耗時和航跡關聯耗時的變化規律不同使得航跡關聯總耗時隨航跡數N和子區域數M的變化呈現不同的變化趨勢。由最優分區數統計結果可以看出，并不是分區數越多，運算量越小，但隨著航跡數N的增加，最優分區數也越來越大。

圖5 航跡關聯總耗時

圖6為N=200時不同分區數下的關聯正確率曲線。由圖6可以看出，在目標密集且均勻分布的情況下，航跡關聯正確率隨分區數量的增加而有所降低，但與不分區時的航跡關聯正確率相比，下降的幅度較小。這是由于劃分目標子區域時，在相鄰子區域設置了重疊區域，抑制了傳感器測量誤差可能帶來的漏關聯和錯關聯。

圖6 N=200時關聯正確率統計

綜上所述，本文提出的分區航跡關聯算法在保證關聯性能的同時能夠大大提高計算速度，在實際工程應用中具有重要的意義。

5 結束語

本文針對多傳感器信息融合系統航跡關聯運算量大，無法滿足工程應用實時計算要求的問題，提出了一種分區快速航跡關聯算法。該算法將目標區域劃分成多個目標子區域，為消除測量誤差對關聯的影響，相鄰目標子區域之間設置了重疊區域，并給出了最優分區數的判定方法。仿真實驗結果表明，本文提出的算法能夠大大降低航跡關聯運算量，且保證了航跡關聯性能，適用于工程應用。