基于時間序列的PM2. 5時空插值算法改進研究
肖亞楠
關鍵詞: PM2.5 時間序列 相關性分析 時空插值
隨著生活品質的提高,“霧霾”一詞越來越多出現在人們的視野里,其主要成分是PM2.5[1]。各地區的PM2.5分布具有季節、地域特征,與溫度、濕度、風速、降雨量等氣象特征之間具有相關性[2]。
PM2.5是典型的時空數據,具有顯著的時間序列特征和地域性特征。現有的PM2.5分析方法中,多將時間和空間特征分割開來,不能充分地利用時空數據的全部特征,分析結果的可靠性較低。
該文基于成都地區氣體污染物觀測數據對基于時間序列的時空插值算法進行了改進研究,并設計了對比實驗,對改進后的算法插值精度進行了評估。
1 研究區概況與現有研究方法的概述
1. 1 研究區概況
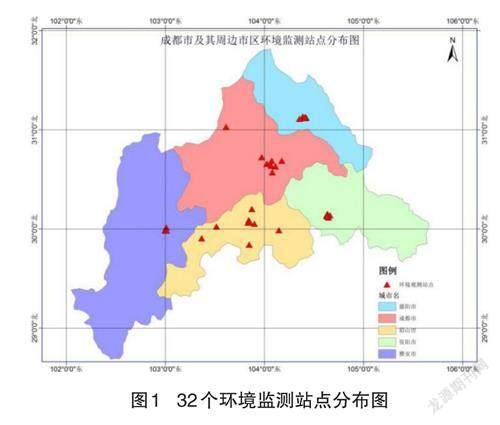
成都位于四川盆地西部,地形地貌復雜,東接龍泉山脈和盆中丘陵,西臨邛崍山脈,中部為成都平原[3],靜小風頻率高,污染物難以及時擴散,此外,該地區近年來發展迅速,基礎設施建設迭代更新較快[4],使得成都地區的PM2.5處于高濃度狀態。該文研究了32 個環境監測站點的數據,這些監測站點位于成都市及周邊的4 個市區,站點分布不規律,局部成簇,分布于北緯28.7°~34.57° 、東經100.82°~105.67°。圖1 為32 個環境監測站點分布圖。
1. 2 數據來源及預處理
該文采用的數據包括研究區域的地理范圍、環境監測站點的位置,待研究空氣污染物指數觀測數據。通過網絡數據訪問方式完成數據獲取,具體為:編程獲取四川省空氣質量監測系統中JSON 格式數據,經解析后得到各觀測站點全天候空氣污染物指數數據(污染物濃度與其指數呈現正相關)。
需要先對空氣污染物指數數據進行預處理,處理結果用于插值分析。
1. 3 既有研究方法概述
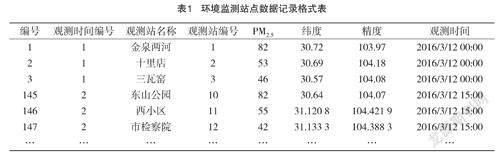
既有的時空插值方法眾多,其中,約減法和擴展法較為經典,兩種算法均能實現對不規則數據集的時空混合插值計算。約減法首先對數據進行時間插值,再進行空間插值[5],該方法只能在時間序列內對觀測站點歷史缺失數據進行插補,對PM2.5 進行歷史數據統計,并對PM2.5的變化規律進行分析,但是不能實現對PM2.5數據的實時監測。擴展法綜合考慮了時間和空間因素,整體性較好,但時空單位的多種組合形式會造成插值結果各異,且不同組合單位之間并不具有換算規律,結果不穩定。該文以約減法為基礎,結合時間序列分析和相關性分析結果,改進PM2.5時空插值方法。表1 是環境監測站點數據記錄格式表。
2 基于空氣污染物之間相關性的相關權重法
約減法將時間間隔作為插值權重,算法基于“等間隔內PM2.5指數變化量相同”的假設,算法執行過程中使用中間時刻對應的前后兩時刻的PM2.5指數估算中間時刻的PM2.5數值。分析發現,PM2.5的時間變化量并不均勻,該權重具有局限性。
2. 1 相關性分析
相關性分析是指使用相關系數定量的分析兩變量之間的相關性,以判斷其關系的密切程度。相關系數的取值在[-1,1]范圍內,為無量綱數,相關程度與相關系數的絕對值正相關,正值表示正相關。該文采用Spearson 秩相關系數和Pearson 相關系數來衡量各空氣污染物指數與PM2.5指數值之間的相關程度。對于變量X、Y 的觀察值xi 和yi,采用式(1)、式(2)分別計算Pearson 相關系數和Spearson 秩相關系數:
式(1)(2)中,xi、yi 為i 時刻兩變量的觀測值;xˉ、yˉ為兩樣本觀測均值;N為變量X與Y的Pearson 相關系數;pi、qi 為兩變量的秩次,N為樣本數量,R 表示變量X 與變量Y的Spearson 相關系數。
2. 2 PM2. 5與主要空氣污染物之間的相關性
CO、O3、SO2、NO2等氣態污染物在擴散過程中可轉換為二次污染物,引起PM2.5指數變化,研究PM2.5與空氣污染物之間的相關性對于描述PM2.5的變化趨勢具有重要意義。楊可鑫[6]、彭菲等人[7]、黨瑩等人[8]、陳菁等人[9]、BRAVO M A 等人[10]和WONG D W[11]等人通過對國內外部分地區空氣污染物暴露水平進行監測和分析,證明了主要氣體污染物與PM2.5的變化趨勢具有相似性。該文定量分析了成都地區PM2.5與主要氣態污染物之間的相關性。
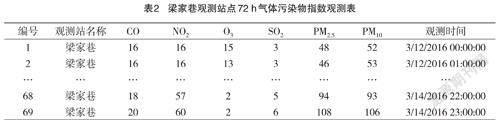
該文以梁家巷觀測展為例進行說明,表2 是各空氣污染物72 h 內的指數觀測值,圖2 是各空氣污染物的變化曲線,表3 是PM2.5與各氣體污染物之間的相關系數。
2. 3 基于空氣污染物相關性的相關權重法
由表3 數據可知,除CO 和O3 之外,PM2.5 與SO2、NO2、PM10 的相關系數均大于0.6,相關性較強。進行PM2.5時間插值時,將其變化程度及變化趨勢作為確定插值權重的參考。
第一步:數據準備。數據預處理,得到長為72 h 的六組空氣污染物時間序列數據結果。
第二步:相關性分析。根據編制好的時間序列數據,采用公式(1)、公式(2)算出這5 種氣體污染物與PM2.5的相關系數Rj,若結果若滿足式(3),則相關性較強,其變化程度數據可作為PM2.5插值權重的參考。
第三步:權重計算。計算待插值時刻氣體污染物指數相對前后兩連續時刻的變化率,該文次采用商表示變化率:
第四步:PM2.5時間插值計算。采用式(5)計算插值結果。
第五步:PM2.5時空插值。分析PM2.5的時、空插值與真值間的相對關系,構建多元線性回歸模型,估算出PM2.5在時空范圍內任意點的數值。
3 基于PM2.5自相關性的函數模型法
相關權重法基于氣體污染物之間的相關性特征,能實現對時空范圍內任意點的插值分析。該方法的局限性在于:第一,只能用于估算首尾時刻之間的PM2.5數值;第二,算法基于“一定時間范圍內,PM2.5與主要空氣污染物的變化趨勢具有相似性”的前提,若參考氣體與PM2.5的相關系數小于0.6 時,則該方法的可信度較低[12]。
傳統時間序列分析方法僅能夠實現指定時刻的數據預測[13],該文研究了PM2.5時序數據的自相關特征,構建了預測模型,實現了PM2.5指數的實時預測。
X = {x1 x2 x24},其中x1~x24 是采樣間隔為1 h的PM2.5時間序列數據集。首先從時間序列數據中計算出趨勢變化特征點,以此特征點為隔斷,將整個序列劃分為多個不等長的子區間,然后對各區間的觀測值分別建立函數估算模型,即:第一步,趨勢變化特征點的確定。對于時間序列X 而言,如果X 滿足條件xp ≤xp + 1 ≤ ≤xi,并且xi ≥xi + 1 ≥ ≥xq (1 ≤p ≤i ≤q ≤n),或者滿足xp ≥xp + 1 ≥ ≥xi且≤xi + 1 ≤ ≤xq (1 ≤p ≤i ≤q ≤n),則xi 為時間序列數據X 的趨勢變化特征點。
第二步,函數估算模型的確定。以趨勢變化特征點為間隔,劃分時間序列子區間,使用函數模型擬合各區間內的PM2.5指數變化趨勢估算任意時刻的PM2.5指數值。采用式(7)、式(8)進行計算。
式(7)(8)中,a1、b1、a2、b2、c 為函數模型中的常數,通過最小二乘法計算得到;Z(t )為PM2.5在t 時刻的指數估算值。
第三步,開展PM2.5 數據時空插值計算。采用式(9)進行綜合考慮時空的混合插值。可估算任意時刻、觀測站點的PM2.5指數值。
4 實驗結果分析
在進行PM2.5時空插值時,第一需要確定時空插值的目的,第二要確定插值的方法。由圖3 可知,針對不同的插值要求和數據情況,分為以下3 種情況進行分別處理。
(1)僅PM2.5 數據缺失,也即SO2、NO2 等其他空氣污染物觀測值完整。該情況下,可計算PM2.5與各空氣污染物指數的相關系數,使用相關權重法修補缺失的PM2.5數據。
(2)所有氣體污染物觀測數據在某一時刻整行缺失。該情況下可以使用約減法進行數據修補。
(3)實時空氣污染物指數值預測。需要編制完整時間序列,進行數據平穩性分析及處理,然后采用函數模型法進行數據值預測。
4. 1 成都市PM2. 5缺失數據修補
截取29 個環境觀測站的連續72 h 的空氣污染物指數觀測數據作為數據源,對其進行了循環計算及交叉驗證。分別采用了相關權重法、約減法、直接函數模型法以及平穩性處理后的函數模型法,對中間段的70個時刻的污染物指數進行逐一插值計算。以平均絕對誤差、均方根誤差即平均相對誤差作為計算結果的評價指標,對各插值算法的PM2.5 修補結果進行精度評價,表4 是指標計算結果。
評估結果反映出:相關權重法的精度最高,經時間序列數據平穩性分析處理后,基于時間序列的函數模型法計算得到的結果精度有提高。試驗表明,各監測站點的計算結果一致,該文將以梁家巷觀測站點為例進行結果展示。圖4 表示不同時刻的PM2.5指數修補結果,圖5 表示不同插值方法的PM2.5數據修補結果的相對誤差分布。
4. 2 成都市PM2. 5數據預測
數據預測前對原始數據進行了預先處理,具體如下。
(1)奇異站點的檢測與觀測數據修補。奇異站點為數據缺失超過3 h 的觀測站,使用時間序列分析法對奇異站點進行PM2.5數據修補。
(2)時間序列插值補充。修補歷史缺失數據,得到完整的時間序列,為實時數據預測做準備。
(3)計算時空插值模型的參數值wp、wt,w。
(4)將第24、36、72 組數據作為“待預測值”,其他組數據作為“樣本觀測值”,對其進行觀測值預測。
該文采用了時間插值方法、空間插值方法以及基于時間序列的函數模型法進行插值計算,表6 是插值精度的評定結果。
4. 3 結果分析
這3 種插值方法的精度由低到高依次為:空間插值算法<時間插值算法<基于時間序列的時空插值算法。其中,基于時間序列的時空插值算法的RMSE 比時間插值法提高了25%,比空間插值法提高了40%。分析其原因:由于研究的環境監測站點分布不規律,且數量有限,導致了空間插值的精度較低;由于用于時間序列分析的原始數據時間分布均勻,且數據量充足,導致時間插值算法的精度較高;時空插值算法綜合考慮了時、空因素對PM2.5指數的綜合影響,該文中對其進行了量化分析,并參與插值計算,故其插值結果精度最高。
5 結論
基于時間序列的時空插值算法的優勢在于:(1)進行時序數據預測時,對時間間隔無要求;(2)考慮了空間因素對空氣污染指數的影響,可以對任意地點、任意時刻的PM2.5 觀測值進行預測。實驗表明,改進后的基于時間序列的時空插值算法從理論和原理上可行。

