如何營造具有生長力的單元復習課
沈寬

1. 問題提出
對大部分學生來說,復習課就是整理知識點和大題量的操練,教師就題講題,這樣的教學模式枯燥無味,缺乏數學本質的教學,更缺乏學科育人的理念。要改觀這一現象,需要教師把學習的主動權還給學生,引導學生經歷知識的“重建——解構——優構”過程,讓學生看清數學本質,優化數學思維,切實提高問題解決的能力及創新意識和實踐能力。那么,到底如何激發學生思維和情感參與,營造具有生長力的課堂呢?筆者以蘇科版教材數學八年級上冊第六章“一次函數小結與復習(1)”為例與大家進行探討。
2. 教學實踐
2.1 展示導圖,梳理知識
2.1.1 教師展示課前讓學生畫好的思維導圖,并給予充分肯定。
2.1.2 追問:展示的思維導圖有沒有可以補充的內容?可否更優化?(通過學生之間互相補充介紹,教師建構、優化表達本章節的思維導圖)
設計意圖:開門見山地利用思維導圖引入課題,改變傳統以教師為中心的教學模式,不僅可以讓學生自主提前復習本章內容、整理知識結構,還能加深本單元知識的理解,起到了思維可視化、知識精煉化、內容結構化的效果。同時,通過師生共同建構后,思維導圖中呈現的從概念——圖像——性質——應用的研究思路,揭示了函數研究的一般方法,為接下來研究反比函數和二次函數奠定堅實基礎。
2.2 復習鞏固,活動交流
2.2.1 回顧知識,建立圖表
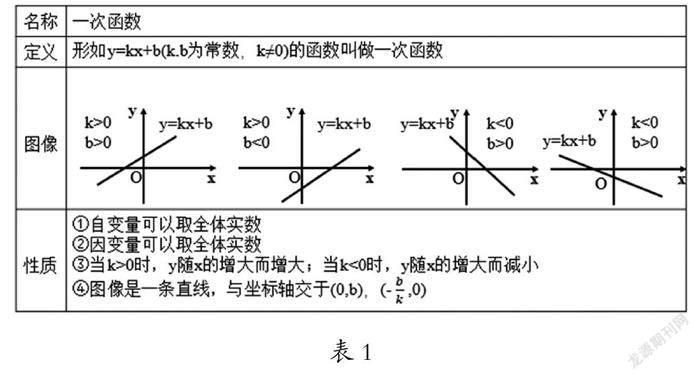
學生講解一次函數的定義與圖像性質,教師適時評價,引導學生歸納成圖表1。
設計意圖:鼓勵學生參與講解,充分奉行學生為主體的教學理念,鍛煉學生的數學邏輯和語言表達能力,增強學生的自信心,激發學生的學習積極性和主動性。表格的構建直觀體現出一次函數的圖像受k, b的共同影響,增減性只受k的影響而與b無關,進而促進學生深刻理解一次函數“數”與“形”的聯系,在歸納的過程中積累數學活動經驗。
2.2.2 深化概念,形成聯系
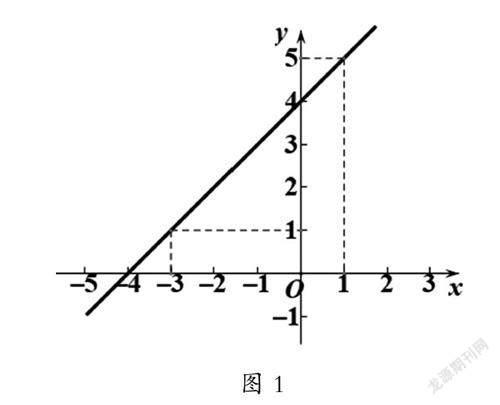
問題1:如圖2,若函數圖像經過(-3,1)和(1,5)兩點,你能求這條直線的解析式嗎?
追問1:在這個過程中,你運用了什么知識和方法?
問題2:你還能從中獲取哪些信息?請你設計一個問題,并對其進行解答.
問題3:若直線y=x+4與x、y軸分別交于A,B兩點,求△AOB的面積.
問題4:若點P在一次函數y=x+4的圖像上,求到x軸的距離為4的點P坐標.
問題5:當x取何值時,y的值大于0?小于0?
問題6:若平面內有另一條直線y=-2x+1,與x軸的交點為C,與y軸的交點為D,試求出yAB>yCD時x的值.
問題7:求兩直線交點與x軸圍成的三角形的面積.
設計意圖:問題1從知識(“數”與“形”的轉化)、方法(待定系數法)、思想(函數思想和數形結合的)三方面進行了考查,教師投屏學生的解題過程并加以評析,提高課堂效率。追問1做出過程性追問,旨在讓學生對行為、想法背后的思維活動進行反思和審視,實現深度學習,提高學生的思維能力。問題2設置問題空白,讓學生自主提問和解答,貼近學生的最近發展區,引導學生深度參與到課堂中來,提高應用知識的能力和教學效率。問題3根據圖形確定出三角形的底和高,學生思維在“數”與“形”之間穿行,然后進行解答。問題4考查了數形結合的應用以及分類討論的思想,既可以從“數”的角度把y=4或y=-4時,代入函數求出x的值來解決,也可以從“形”的角度根據k=1時直線與x軸所夾的銳角為45°角,利用等腰直角三角形的性質來解決。問題5到問題7是由一次函數生長出的與一元一次方程、一元一次不等式、二元一次方程組的聯系,本質上是函數變化的特殊情況,加深了學生對“數形結合”思想的認知。整個過程中,通過不斷添加條件,設置問題串聯知識,步步推進,讓學生感受到數學知識的生長過程,有利于培養學生數學思維的發散性、廣闊性和深刻性。
2.2.3 變式拓展,發散思維
變式1:求直線y=x+4向上平移2個單位后的直線解析式
變式2:求直線y=x+4向右平移2個單位后的直線解析式
變式3:求直線y=x+4關于x軸對稱后的直線解析式
變式4:求直線y=x+4繞它與x軸交點逆時針旋轉90°后的直線解析式
變式5:若點P 是y軸上的一個動點,過點P的一條直線PQ交AB于點Q,將點B沿著直線PQ翻折,若點B恰好與點E重合,請求出此時的直線PQ解析式.
設計意圖:初中階段主要研究平移、旋轉、翻折這三種變換,在平面直角坐標系中我們可以引導學生多樣化的探究函數圖像。通過變式1和2的探究,讓學生明晰問題的本質,加深對“待定系數法”的理解和靈活運用。變式3和變式4對問題進行了拓展,通過引導學生觀察變換前后的函數圖像,揭示問題本質屬性,解題思路與剛才變式1和2基本一致,提高思維的延伸性和靈活性。在問題的循序漸進中,學生已逐步把握解決此類問題的突破口——找關鍵點。變式5可以和學生一起從知識(翻折變換)、方法(方程與勾股定理)、思想(全等變換、方程思想)三個方面進行歸納,把思維引向深處,感受知識的生長和發展過程,為學生提供運用綜合知識解決問題的機會。要注意的是,教師在引導學生解決問題后,可以把提問方式進行結構化處理,即多問學生是怎么想的,運用了什么知識和方法?引導學生通過問題不斷反思,提高數學能力。
變式6:函數y=x+4的圖像上是否存在一點P,使
S△AOP=S△AOB?若存在,求出點P坐標;若不存在,請說明理由.
變式7:若兩直線交點為點E,是否存在y軸上一點P,滿足S△EBD=S△BEP?若存在,求出點P坐標;若不存在,請說明理由.
設計意圖:在學生熟悉函數y=x+4后,植入面積問題,發散學生思維。變式6是兩個同底直角三角形的面積關系問題,本質上就是兩個直角三角形的高的關系,進而可以得到點P的橫坐標,解決問題。變式7可以引導學生按照方法1“同底等高的兩三角形面積相等——構造平行線——求平行線表達式——求點P坐標”,或者方法2“把斜三角形BEP轉化成有橫平豎直線段的三角形面積和差問題求出點P坐標”. 在一題多解和多解歸一中不斷探尋,讓學生在問題中意識到,對于這類直線上的動點問題,求三角形面積所需要的底或者高,歸根到底還是一次函數和坐標軸的交點問題,從而打破難點,豐盈了數學經驗,提升了數學素養。
2.3 課堂小結,積累經驗
教師引導學生從基礎知識、解題方法、數學思想三個維度對本節課進行歸納總結,盤點收獲。
數缺形時少直觀,形少數時難入微。
——華羅庚
設計意圖:引導學生回顧反思,感悟數學,感悟函數蘊含的基本知識,感悟函數滲透的數學基本思想,積累函數運用的數學經驗,進而提升數學能力。最后引用數學家華羅庚先生的名句,增強學生的民族自豪感,激發學生的學習熱情,引起強烈的情感共鳴,達到課雖終、意未盡的效果。
3. 教學思考
3.1 活用思維導圖,建構知識體系
復習課上知識點的掌握是關鍵的,它是解題之源、思維之本。若只是孤立地看待教材上的知識點,它們是零散、瑣碎的。因此需要教師充分研究教材,引導學生以章節、板塊的角度整體把這些細碎的學習內容“組織”起來,形成有一定關聯的知識網絡,才能更有效地幫助學生進行學習。思維導圖就是一種很好的整理方法,通過讓學生課前自主對知識進行梳理分析、歸納總結、理清知識脈絡、形成知識結構框架,然后在課上對比探索、交流展示、深挖知識點,有序推動學生數學思維的發展,促進深度學習,讓學生的認知達到“既見樹木、又見森林”的效果,培養思維的廣闊性、發散性。
3.2 設計關鍵問題,引發深度學習
從教育的角度來看,數學思維比數學知識更重要,因此教師要精心備課,在教學設計時把學生的核心素養放在首位,設計體現數學本質與意義的問題,以思維為導向,促進學生知識結構的螺旋式上升。在這節復習課中,始終圍繞y=x+4這條主線,以提升學生的深度學習能力作為暗線,摒棄傳統的題海戰術,通過關鍵問題和變式拓展,巧妙地把本章節的零散知識點都串聯起來,并在原來的問題上不斷“生長”出新的問題進行研究,引導學生思維不斷走向縱深,讓學生感受知識、方法、經驗、思維的自然生長,提升思維品質、積累數學活動經驗,達到深度學習的效果。
3.3 注重方法梳理,提升數學素養
從知識到能力、從能力到素養依次提升,這是數學教育所追求的目標。學生的數學基本技能、基本思想和方法都是在解決問題的過程中獲得的,教師在教學時要注重研究方法的梳理和研究思路的提煉。一次函數是最具代表性的基本函數,教師在引導學生分析問題、解決問題之后,要啟發他們回過頭反思問題解決的過程,感受一次函數的研究思路,抽象出數形結合、分類討論、數學建模、轉化等基本思想方法,積累活動經驗。在舊知回溯中求新、在求新發展中反思,不斷提高學生思維能力、實踐能力和創新意識,幫助學生增強“四基”,提升“四能”。只有提升課堂的立意,才能真正有效地提升學生的學科素養,實現學科育人的價值。

