讓數學課堂共生思維之花

滕莉祥

問題是數學的心臟，問題也是數學課堂的靈魂，零散分離的“壞”問題不能發展學生的思維，只有經過精心設計、層次分明的“好”問題才可更好地引發學生深層思維，發展學生的思維品質。巧妙地設計問題串，可使不同層次的學生思維都得到連續地、系統地訓練，使每一位學生的思維都得到更好地發展。下面筆者就此談談在數學課堂中運用“問題串”教學的意義。

一、巧設問題串，激發學習興趣，提升“發散思維”能力

為激發學生學習數學的興趣，教師要引導學生用數學的眼光觀察生活，用數學的思維思考世界，將數學與生活巧妙聯系，為學生鋪設適度的“問題串”臺階來調動學生的學習積極性，學生通過一步步攀爬，逐步領悟數學本質，鍛煉數學發散思維能力。

案例1：蘇科版數學七年級《從問題到方程》這節內容，其本質是將未知數和已知數享有同等的地位參與數式的運算，從而打開已知和未知之間的通道，達到解決問題的目的。核心是要尋求已知量與未知量間的等量關系，為了讓學生更好地感受方程是刻畫現實世界的有效模型，設計如下主題式問題串：

同學們，學校準備組織部分同學去春游活動，小明是本次活動的負責人，你能幫助他解決下列問題嗎？

問題1：某校組織七年級80名優秀學生到玄武湖劃船，一共租了30條船，其中每條大船可坐4人，每條小船可坐2人。如果小船有x條，那么可得什么方程？

學生1：根據題意我們可以得到以下數量關系式：大船容納的人數+小船容納的人數=90，故得方程2x+4（30-x）=90

師：回答得非常好。經過討論決定此次春游自帶水果，你能幫小明管好后勤嗎？

問題2：計劃用班費90元買蘋果和香蕉共30斤，已知蘋果每斤4元，香蕉每斤2元。如果買了x斤香蕉，那么可得什么方程？

學生2：由于本題的等量關系是：香蕉的總價格+蘋果的總價格=90。香蕉的總價格是2x，蘋果的總價格是4（30-x），因此可以得到方程2x+4（30-x）=90

師：春游回來正好發現學校在舉行球賽，有一個關于球賽的問題需要你們來解決。

問題3：某球隊參加聯賽，勝一場得4分，負一場得2分，該隊賽了30場，共得分90分，請問該隊負了多少場（用方程表示）？

學生3：本題的等量關系：勝的場數×4+負的場數×2=90。 解設該隊負x場，則勝（30-x）場，可得方程2x+4（30-x）=90

問題4：同學們開動腦筋，回答得都不錯，仔細觀察剛剛解決的這三個實際問題，你有什么發現？

學生4：通過觀察發現列出的幾個方程長得一模一樣，都是2x+4（30-x）=90。雖然實際的問題情境不一樣，但是運用方程解決問題時挖掘出來的數學本質都是一致的。

師：是的，數學之美在于它的智慧和簡潔，同一個方程模型往往可以描述現實生活中不同的問題背景，但萬變不離其宗。

問題5：聯系生活情境你能不能自己也編一道題目，使得能用模型2x+4（30-x）=90來解決？

學生思維活躍，各抒己見，最后發現這樣的實際情境可以有無數個，只要抓住等量關系就可以，從而達到理解模型，理解數學本質，體驗在生活中學數學、用數學的價值。

上述案例以“春游”為主題設計問題串，將游戲問題、購物問題、球賽問題等實際生活中的常見情境串在一起，將知識與情感有機地整合到課堂教學中，通過變化不同的問題背景，將不同問題的“解法歸一”，經歷將實際問題數學化的過程，讓學生深度思考，思維生長。

二、巧設問題串，喚醒思維起點，提升“創造思維”能力

奧蘇伯爾認為，當學生把教學內容與自己的認知結構聯系起來時，意義學習便發生了。教學時先需喚醒學生已有的認知經驗，在此基礎上引導學生通過轉化、遷移、類比、分析、應用等策略解決新的問題得到新的學習經驗。教師要充分了解學情，有針對地設計與學生認知經驗相符的“問題串”，幫助學生理解同化新的知識，激發學生的創造思維。

案例2：蘇科版數學九上《5.1二次函數》是整章的起始課，與前面學習一次函數、反比例函數的套路一以貫之。喚醒了學生如何學習一次函數的記憶，也就能順理成章地突破二次函數重難點，知道如何研究新的知識，提升學生的創造思維。

問題1 ：寫出石塊落入水中蕩起的波紋向外擴展形成的圓形面積S與半徑r之間的關系式。追問：這可能是一個什么函數？

用熟悉的生活情境說明二次函數存在于生活中，讓學生產生探究的欲望，產生學習的需要。

問題2：我們曾經已經研究過哪些函數？

喚醒學生思維起點，與已有的認知結構架構橋梁。

問題3：同學們回憶一下，我們當時是如何研究這兩類函數的？

不斷追問逼著學生回憶起點，一次函數、反比例函數的研究方法可以創造性地遷移到新的函數的學習中來。

生1：我們研究一次函數的表達式，還有它的函數圖像、性質、應用。表達式通過具體的實際情境得來，由特殊到一般，得出一般的形結構而且一定要加上成立的條件。

生2：畫函數圖像的一般步驟為：列表，描點，連線。

問題4：同學們回答得很好，前面的知識掌握得非常扎實，對于剛剛遇見的這類新函數，你們現在會研究它們了嗎？

同學們大受啟發，撥云見日如醍醐灌頂，知道了研究任何一類沒見過的函數都是按照相同的方法。為后面新知的學習開啟了愉快的學習之旅。

在數學教學中不斷滲透數學研究的“基本套路”，顯化基本套路，培養學生對基本套路的認識和把握，從方法上給學生帶來啟發與思考，幫助學生發展創造性思維。

三、巧設問題串，完善知識結構，提升“邏輯思維”能力

法國數學家托姆認為學習知識不是死記硬背可得的，而是以智力參與主動探究建構的過程。教師在教學中要善于設計具有探究意義的問題串，讓學生的思維在探究中得到發展和升華。

案例3：蘇教版八年級下第九章中心對稱圖形復習課（第一課時）筆者設計了如下問題串：

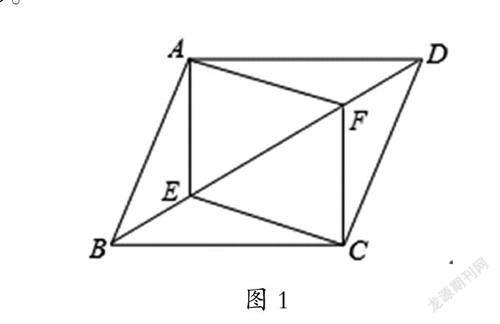
問題1：如圖1，在四邊形ABCD中，點E、F在BD上，且BE =DF， 若四邊形ABCD是平行四邊形。求證：四邊形AECF是平行四邊形。

本題考查平行四邊形的判定方法，從邊、角、對角線出發共四種判定方法。本題中幾乎每一種判定方法都可以解決，但在一題多解的過程中，教師要引導學生盡可能尋找最簡單的方法解題。

問題2：若四邊形AECF是平行四邊形，則四邊形ABCD是平行四邊形嗎？說說你的理由。

問題3： 要使四邊形AECF為矩形，還要添加哪些條件？

問題4：如果在原條件基礎上增加AB=AD，那么四邊形AECF是什么圖形？證明你的結論。

問題5：在變式3的條件下，連接AC交BD與點O，若AB：BE：AO =13：7：5，求證：四邊形AECF是正方形。

通過設計上述“問題串”，層層遞進，環環相扣，貫穿整章知識結構。問題1和問題2鞏固平行四邊形的判定方法；問題3在問題1和問題2的基礎上聯系了平行四邊形與矩形的關系，復習鞏固矩形的判定方法；問題4回顧了平行四邊形與菱形的關系，強化了菱形的性質和判定方法；問題5則將正方形與菱形、矩形、平行四邊形都聯系起來，復習其內在的轉化關系。緊緊圍繞一個例題把本章的所有知識點都串聯起來，通過“問題串”不僅完善了學生的知識結構，還鍛煉了思維能力，提升了學生的邏輯思維水平和整體思維觀。

四、巧設問題串，內化問題解決，提升“反思思維”能力

著名的數學家波利亞在他的《怎樣解題》一書中詳細介紹了問題解決的四個步驟：弄清題意，擬定計劃，執行計劃，回顧反思。在數學教學過程中，教師往往較重視前三個步驟，而對回顧反思不是很重視，通過合理設計問題串，加強回顧反思，從而提高學生反思思維能力。

案例 4： 探索三角形全等的條件（起始課）為使學生對本章節的總體內容和框架有一個全面而大致的了解，筆者在本節課的最后幾分鐘提出了以下問題：

問題1：通過本節課的學習，你有哪些新的收獲？

問題2：在數學活動經驗方面你有哪些新的成長和體會？

問題3：本節課中滲透了什么數學思想？

問題4：在證明的過程中有哪些注意事項和規范性要求？

在問題 1中，學生通過推理論證大致得到了判定三角形全等的條件至少需要三個：當滿足三邊對應相等或者兩邊及其夾角對應相等或者兩角及其夾邊對應或者兩角及其一角的對邊分別相等時可以判定全等。在問題 2和問題3中，學生從簡單到復雜進行思考，從一個條件出發，然后兩個條件、三角條件以此類推找出最簡單的判定條件，通過舉出反例或用尺規作圖加以驗證猜想及結論，學生抓住“邊”和“角”兩個維度，對邊和角的個數進行分類探討，體現分類討論的數學思想方法。基于三個條件的分析，通過對邊或者角的個數進行分類，學生可以得到以下六類情形：三條邊；兩邊一角（夾角或一邊的對角）；兩角一邊（夾邊或一角的對邊）；三個角。對每一類情形分別深入細致思考，想一想、畫一畫、動手操作，尺規作圖、舉出反例等驗證結論的正確性。這種分類討論、操作實驗的研究方法在數學解題中常會用到。

在問題4這一環節中，教師設置“問題串”引導學生對數學學習進行反思總結，積累豐富的數學活動經驗，滲透思想方法，前后一致、一以貫之，體會學習數學的樂趣及反思的必要。只有學會反思，才能不斷完善和成長！

數學教學的一項重要使命就是啟發學生學會思考，培養學生數學的眼光、數學的思維和數學的語言。課堂以問題作為載體，而高效、有意義、有層次的問題更能引發學生積極思考，發展思維能力，通過設計有價值的“問題串”提高課堂效率，開發學生的思維能力，優化育人的效果，為學生營造出個性化的生態課堂，讓數學課堂共生思維之花！