淺談信息技術對初中數學動態問題教學的優化

吳文敏

初中數學教學中，“圖形與幾何”作為主要教學內容，需要培養學生的空間想象能力與分析能力，提升學生的分類討論思想與數形結合思想。在此以初中數學動態問題教學為例，教師利用信息技術手段輔助教學，能夠幫助學生直觀地了解圖形變化過程，進而理解題目中各種變量的關系，為幾何教學注入新的活力。基于此，本文先討論在初中數學動態問題教學中運用信息技術的優越性，然后從審題、猜想、驗證、實踐的角度探究如何將信息技術運用到動態問題教學中，旨在通過此為教師開展解題教學提供參考。

一、初中數學動態問題教學中使用信息技術的優越性

信息技術在解決動態問題的優越性主要體現在：第一，能夠更直接地呈現問題中點變化時圖像的變化，激發學生的積極思維。在傳統動態問題教學中教師只能在黑板上做出靜止的圖形，精準度還不足，學生難以感受到動態問題中的運用過程，不能感受圖形的位置變化，導致在解動態問題的時候容易產生為難情緒，放棄學習。但是在信息技術的使用后，讓學生能夠加強對圖形變化的感知，直觀了解位置與數量的關系，減輕學生的解題壓力。第二，借助信息技術還能開闊學生的解題思路，培養數學素養。學生在做中考試卷的時候不能借鑒輔助工具，需要在頭腦中形成動態思維解答問題，此需要學生掌握一定的動態思維。所以在課堂中運用信息技術開展解題教學，可以讓學生在觀看的時候主動思考問題，產生跳躍思維，自然地找到解決方法，靈活建構知識。第三，借助信息技術實施解題教學還能提升教學效率。進行動態問題教學時，教師除了講解問題還要繪圖、書寫板書，此大大占用了課堂時間，影響教學效率。而信息技術的運用能直接借助多媒體展示圖畫與板書，減少教師繪畫與書寫的時間，繼而有更多時間深化問題，讓學生探究思考，進而能夠提升教學效率。

二、初中數學動態問題教學中信息技術的運用策略

（一）借助信息展示動態問題，弄清題意

有時學生受讀題能力的影響，在讀題后不能有效挖掘條件，或者出現理解錯誤。特別是當學生面對動態問題的時候，難以有效聯想動點、動線、動角等。教師針對此的教學如果使用傳統的教學手段，難以讓學生了解點或者線的運動過程，當然題目中包含的隱含條件更是難以發現。另外受初中生直觀想象能力的影響，還不能將題目中的未知與已知條件結合推敲聯想。基于此，學生難以找到數學動態問題的解題途徑。

信息技術的運用，能夠為學生清晰地展示動態問題，有效挖掘幾何動態問題中的隱藏條件，繼而找到未知與已知條件之間的關系，找出問題實質。另外如果題目中包含大量的干擾信息阻礙學生解題思路的探究時，在借助信息技術中動態數學技術的時候還能清晰地為學生展示圖形中動態元素的變化，加強對問題的理解。

例如問題：如圖1，在直角三角形ABC中，∠C=90°，直角邊AC與BC相等，為4，點P是直角邊AC上的一動點，沿著直線BP折疊三角形BPC，點C的對應點是點D，此時在折疊的過程中點D的路徑長是________。此類動態翻折類的問題解答時，需要學生先弄清題意，在傳統教學中，教師難以為學生展示隨著三角形的折疊點D的變化，單靠學生自己的想象也難以想象出畫面。但是借助動態數學技術，則能夠清晰地展示三角形折疊的全過程，并能夠發現隱含條件，即三角形BPC沿著PB折疊后，△BCP和△DBP一直是全等的，此時PC=PD，BC=BD。

（二）借助信息展示關鍵信息，助力猜想

初中數學教材中幾何知識的呈現是通過嚴謹的證明得到的，而利用相關知識解答動態問題的時候，我們根據波利亞解題理念要先進行猜想，即在學生找到題目中的已知條件和未知關系以及它們之間的聯系后，就可進行合理的猜想。而在傳統的動態問題解題教學中，教師使用傳統的手段難以幫助學生找出題目中的關鍵要素，再加上初中生的空間想象能力比較薄弱，所以很難獲得正確的猜想過程。所以在解答動態問題教學中，幫助學生找到題目中已知與未知量的內在關系是教學難點。運用動態數學技術能夠為學生動態性地展示題目，幫助教師快速解決教學難點。實際教學中，教師可利用信息技術動態數學教學技術中的“跟蹤軌跡”功能，對幾何圖形進行動態化地處理，如此突破學生的動態想象障礙，在幾何圖形的動態變化下，對題目中的未知建立與已知條件的聯系，實施合理的猜想，繼而產生解題思路。

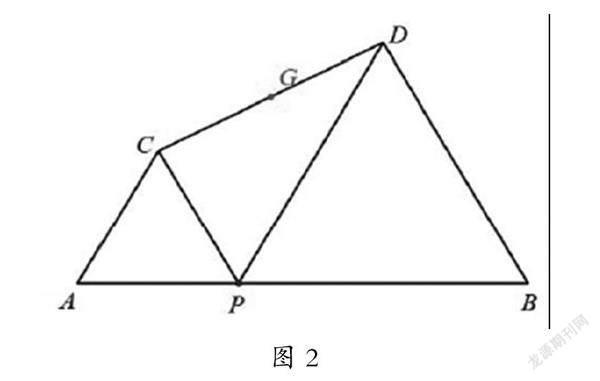
例如問題：如圖2，線段AB的長為10，點P是線段AB上的動點，然后以安AP和PB為邊分別做△APB和△PBD（△APB和△PBD在線段AB的同側），連接CD，G是CD的中點，點P從點A出發向點B出發過程中，點G的移動路徑長是________。此題中是雙動點問題，教師在教授學生“擬定計劃”的時候，提出問題：“點P是主動點，點G是從動點，在點P從A向B運動時，點G的運動路徑是什么？”請學生先聯想思考。然后針對沒有想象出來的學生，需要教師再進行引導：“動點G的移動路徑跟另一個動點P的路徑相同嗎？”“你能嘗試取幾個特殊點嗎？”請學生畫出草圖探究。若還是有的學生不能合理猜想，就可以運用動態數學技術為學生展示動點P的幾個特殊位置（與A點重合、與B點重合，在AB的中點上），然后觀察點G的運動軌跡是直線。繼續提問：“動點的運動軌跡是直線還是圓弧？”此時學生已經可以對自己的猜想有很大的把握，最后在信息技術中動態數學技術的運用下，讓學生確更好地猜想點G的運動路徑——直線。

（三）借助動態演示解析題目，深化解題

在學生們合理猜想之后，就進入到驗證猜想環節中，在此需要找到幾何動態問題中的已知與未知的關系。動態問題往往綜合性強，讓學生難以確定已知數據與未知量的內在聯系，特別是在傳統的解題教學中，教師難以邊講解邊展示圖形運動的過程，在此若結合信息技術展示幾何圖形的動態變化過程，能夠幫助學生更深入地理解問題，解題教學達到事半功倍的效果。

例如問題：如圖3，平面直角坐標系中有一個矩形OABC，點A和C都在坐標軸上，點B的坐標為（2，），在矩形邊BC上分別取點E和F，讓三角形CEO沿著OE翻折，再將三角形BFA沿著AF翻折，此時點B落到點G上，得到的三角形為AGF，如果∠OGA=90°。（1）求過點A、O、G的二次函數的解析式與對稱軸。（2）二次函數的對稱軸上是否存在點P，令△OPG是等腰三角形？在同學們解答完第一小問，確定拋物線的解析式與對稱軸之后，在求點P的坐標的時候，教師要先使用動態數學技術中的“隱藏”功能，將△OPG之外的矩形OABC、△AGF和OGE的圖形隱藏，讓學生直接減少對無關信息的干擾，然后利用動態數學技術中的“繪制”功能，以點O為圓心、G為圓心，OG為半徑做圓，圓與拋物線對稱軸的點為點P，以此找到點P的坐標。

（四）通過動手操作，積累解題經驗

新課程標準要求教師在設計課程的時候融入現代信息技術手段，在解動態問題的時候，還希望學生能夠利用信息技術手段有效思考問題，以此優化教與學的方法，讓學生能夠主動投入到探究性的學習活動中。對學生數學分析能力的培養不是一朝一夕能夠完成的，需要循序漸進，讓學生逐漸積累數學活動經驗，更好地了解數學問題中的包含的規律。所以在解題教學中教師要為學生創造適合的條件，引導其觀察、猜測、推理與解答，豐富數學活動經驗。

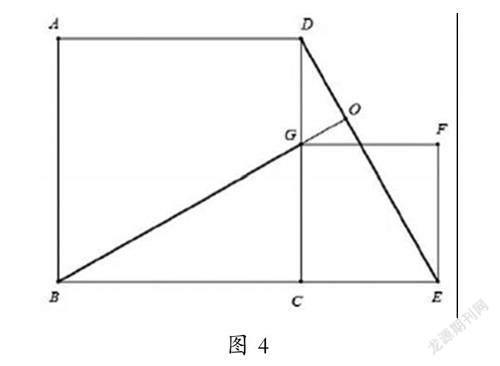
例如問題：如圖4，點G是正方形ABCD中CD邊上的動點，以CD為邊做正方形CGFE，連接DE與BG，求線段DE與BG的關系？在學生們解答完問題后，對此類問題產生了初步認知，教師再設計變式題繼續幫助學生鞏固知識，請學生自主操作，積累解題經驗。變式一，將原題中的正方形CGFE圍繞點C旋轉一定角度后，請問原題中的線段DE和BG的關系還存在嗎？變式二，原題中的正方形變為矩形，兩個矩形邊的關系為：AB=x，BC=y；EC=kx，CG=ky（x和b≠0，k>0），然后提問線段DE與BG的關系？矩形CGFE圍繞點C旋轉一定角度后，請問原題中的線段DE和BG的關系還存在嗎？請學生利用動態數學技術改變題目條件，自主實踐探究，找到問題的答案。

三、初中數學動態問題教學中信息技術的運用實踐

以圖形旋轉類問題為例，問題為：點G是正方形ABCD中CD邊上的動點，以CD為邊做正方形CGFE，連接DE與BG，求線段DE與BG的關系？教學過程為：第一，借助信息技術手段幫助學生弄清題意。使用動態數學技術，在圖4的基礎上，設置點G為CD上的動點，使用“變量尺”功能控制點G的位置，讓其能夠在線段CD上運動，請學生觀察，輔助其理解問題。第二，引導學生進行合情猜想。在學生審題之后，發現不能直接利用已知條件求出線段DE與BG的關系。在此教師要引導學生先猜想線段BG和DE的長度與位置關系，受其空間想象能力的影響，運用線段動態數學技術讓學生觀察，如將圖中的線段BG和DE變藍加粗，然后延長線段BG與DE相交于點O，然后拖動點G，觀察隨著點G 的變化，兩條線段長度的變化、∠BOD的大小變化，如此獲得猜想。第三，動態演示深入理解。結合問題中的條件，引導學生嘗試證明剛剛的猜想。先證明猜想BG=DE，即證明它們所在的三角形GCB和ECD全等，根據三角形全等的性質得到BG=DE。再證明猜想BG⊥DE，可以制作輔助線DE’⊥DE與AB相交于點E’，然后證明DE’∥BG，繼而推導出DE⊥BG。很多學生因為不能想到做這個輔助線，此時教師可以運用幾何畫板為學生演示三角形CDE繞點D逆時針旋轉90°的動畫，最后點A和點C重合，點E落到線段AB上直接與E’重合，以此能夠加強學生的理解，并指導為什么制作輔助線DE’。

通過在初中動態問題教學中運用信息技術策略的研究，討論動態問題教學的優化路徑，可以有效提升動態問題教學效果，為提升教師教學質量提供可行參考。同時通過信息技術的運用還能幫助學生提升解題能力，建立積極的數學學習情感態度，為培養學生的數學核心素養提供參考。