基于PBD 算法的海上補給裝備柔性體仿真技術

李楠, 任鴻翔

(1. 海軍勤務學院，天津 300450; 2. 大連海事大學，遼寧 大連 116085)

0 引言

海上補給是提升海軍艦艇的續航力和作戰半徑的有效手段[1]。海上補給裝備系統復雜，技術要求高，訓練難度大。開展仿真訓練成本較低、效率較高。目前開發的海上補給仿真訓練系統在訓練架設索道的環節中，一般采用兩端掛點實時距離計算并進行直線連點的方式[2]，與補給實際過程嚴重不符，無法模擬由于橫風載荷和船體搖擺等帶來的索具振動，導致官兵在訓練時，無法開展索具振動控制技術訓練。

索具等柔性物體建模的研究始于20 世紀初，在當時的計算條件和數值仿真技術條件下，對索具的研究僅限于穩態特性。隨著計算機計算性能的大幅提升，對索具的研究也有了深入提高。目前索具類柔性體主要使用的動力學模型包括：靜力學平面非線性模型、質量彈簧系統模型、有限元模型和多體動力學模型等[3]。

基于位置動力學(PBD)算法具有穩定性強、允許較大的時間步長以及較好的收斂性等優點。本文從多體動力學模型出發，建立補給裝備索具柔性體模型，并運用PBD 算法開展海上補給裝備索具視景仿真研究，旨在提高海上補給仿真訓練系統的真實感和訓練效能。

1 海上補給裝備柔性體仿真建模

1.1 索具多體動力學模型

索具多體動力學模型是將繩索離散成若干索具段，每個索具段視為剛體，各索具段之間由連接件連接便可建立一個多剛體系統[4]。

索具多剛體動力學模型的基礎上，在索具單元之間的連接件上添加適當的阻尼和彈性形變，如平移阻尼、平移剛度、旋轉阻尼、旋轉剛度陣等幾種矩陣，使剛體單元之間的聯接變成柔性連接，從而將索具的多剛體動力學模型轉化為索具剛柔混合動力學模型[5]。

在此基礎上，進一步將各索具單元進行柔性處理成為具備6 階模態向量的柔性簡支梁，剛柔混合體系統就轉換成了多柔體系統[6-7]。

海上補給裝備柔性體包括高架索、牽引索、輸油軟管等，動力學特性均與繩索相近。因此，本文采用索具多體動力學模型建模方法進行海上補給裝備柔性體視景仿真建模。

1.2 海上補給裝備柔性體視景仿真建模

海上補給裝備中柔性體包括輸油軟管、高架索、牽索、引纜等。其運動形式屬于三維動態運動，為準確反映其運動，在建模時將索具視為剛柔混合體系統。如圖2 所示，將索具在空間上離散為N段單元索具段，索具段之間通過無質量的質點連接，將所有外載荷(阻力、重力、浮力等)的作用集中到索具段上，并計入慣性質量的影響，建立索具段點的運動方程組，通過相應的數值計算方法求[8-10]。

應用牛頓第二定律，得到索具節點的基本運動控制方程：

式中：Mi為索具節點的質量矩陣，包括索具節點自身的慣性質量mi和其在流體中的附加質量Mai；為第i個節點的加速度；Fi為作用于節點i上的外力，包括索具節點的張力ΔTi、內部阻尼力ΔCi、浮力Bi和重力Gi等。式(1)中的mi、可以表示為

式中：Pi為3×3 階單位矩陣，ωi為繩索單元轉動慣量；ln為節點間未拉伸長度；ρ為繩索材料密度；Ca為附加質量系數；si為為微元段的橫截面積；Pi為微元段在浮動坐標系上的投影，下標i-1/2和i+1/2 分別表示節點i-1 到i、節點i到i+1 之間的物理量，如li+1/2=si+1-si表示節點i到節點i+1 間的長度；θ、φ分別為浮動坐標系與地球坐標系之間的夾角。

索具動力學模型解算如圖1 所示。

圖1 柔性索具動力學模型解算流程Fig. 1 Computation flow of the dynamic model of the flexible rigging

2 海上補給裝備柔性體視景仿真

利用多體動力學建立的海上補給裝備索具等柔性體模型，通過計算，可以很好地反映索具的拉伸、彎曲、扭轉等變形效應，但在三維可視化仿真中，實時解算仍存在迭代次數多、收斂難、失效性較差等問題，而在使用PBD 方法模擬索具，需要多次迭代才能使索具的距離約束條件收斂，容易引起模擬的索具產生彈性失真。本文在普通索具模擬的約束條件中增加長距離約束、引腳約束等約束，從而解決了海上補給裝備柔性體在視景仿真中失真的問題。

2.1 PBD 算法概述

在PBD 方法中，索具用約束耦合的粒子表示，在每個時間步長中迭代地求解這些約束條件[11]。對索具粒子的模擬迭代計算分為3 個步驟：1)根據速度和外力移動索具粒子；2)使索具粒子滿足約束條件；3)基于給定數據和時間步長Δt，執行時間 積分。

索具粒子由N粒子和M個約束組成。粒子i∈[1, ···,N]的質量為mi、位置為xi和速度為xi，約束j∈[1, ···,M]有如下5 種特性：

1)約束基數nj，即第j個約束影響的粒子數目為nj。

3){i1,… ,inj}，ik∈ {1,… ,N}。

4)約束對應的剛度參數kj∈[ 0,1]。

5)約束類型分為單邊約束Cj(xi1, …,xinj)≥0與雙邊約束。

在模擬步驟中初始化索具粒子的位置，速度和質量倒數。把所有不能轉換為位置約束的力(如重力)記為fext(xi)，并根據fext(xi)的值進行一次數值積分預測速度vi。然后直接對速度進行衰減操作模擬阻尼。計算完速度后再計算位置的預測值pi。在迭代計算的每個時間步長中生成附加的碰撞約束Mcoll，碰撞頂點的數量決定了碰撞約束Mcoll的數量。得到M個內部約束和Mcoll個外部約束之后，對這些約束進行迭代求解，得到校正后的粒子位置。最后根據摩擦和恢復系數修改速度vi。

2.2 海上補給裝備柔性體的約束設置與計算

海上補給裝備柔性體在橫風、船體搖擺、懸掛重物移動等外部載荷作用下，會出現拉升、彎曲、附著、碰撞等變形。能否在視景中逼真模擬以上各種柔性體變形是衡量海上補給仿真訓練系統逼真度高低的重要指標[12]。

PBD 方法通過修改索具粒子的位置關系，可以模擬出索具等柔性體拉升、彎曲、附著、碰撞的變形。在模擬柔性體拉升、彎曲時，本文使用了拉伸約束、彎曲約束，避免了索具的過度拉伸和彎曲失真；在模擬柔性體和附著物連接時，使用了長距離附著物約束和單邊引腳約束，避免了附著物的拉伸變形失真，附著物與柔性體連接點的兩個粒子合并為一個粒子進行計算[13-14]。

2.2.1 海上補給裝備柔性體拉伸約束的設置與計算

海上補給裝備中的高架索是實施航行橫向補給時作為承載質量的索具。在補給過程中，始終呈現緊張狀態。在其上要懸掛輸油軟管鞍座或干貨行車，并承受橫風、船搖等載荷，因此，在仿真過程中，需要實時計算其張力，并保證其柔性拉伸狀態隨載荷變化而產生拉伸變形。本文使用拉伸約束，考慮高架索為鋼索，抗拉伸能力強，因此設置拉伸約束系數為1，仿真效果如圖2 所示。其中圖2(a)顯示的是高架索的組成粒子及受力情況(綠色矢量為高架索垂直方向上的力，黃色矢量為高架索水平方向上的力)，圖2(b)為高架索組成粒子的蒙皮截圖，圖2(c)為高架索的仿真效果。

圖2 海上補給裝備高架索拉升效應視景仿真效果Fig. 2 Visual simulation results of the hoisting effect of the viaduct of the replenishment equipment

2.2.2 海上補給裝備柔性體彎曲約束的設置與計算

除了拉伸效應外，在海上補給裝備柔性體仿真中也要考慮彎曲效應。柔性體模型上3 個相鄰粒子位置可以決定柔性體的彎曲效果。p1、p2、p3為柔性體3 個相鄰粒子，以p1、p3連線為基準線，通過計算p2距基準線的距離來確定柔性體的彎矩程度。由于粒子數量和解算率的不同，可能會出現柔性體彎曲效果失真。為此需要增加彎曲約束來保證仿真效果。

輸油(水)軟管是海上補給裝備，在橫向補給過程中用于輸送油(水)液貨的柔性體設備。其具有高抗彎曲度但低拉伸剛度的物理特性，因此在添加拉伸約束和彎曲約束時，取拉伸約束值較低，約為0.5，取彎曲約束值較大，約為0.8，仿真效果如 圖3所示。其中圖3(a)顯示的是輸油軟管的組成粒子及受力情況(綠色矢量為高架索垂直方向上的力，黃色矢量為高架索水平方向上的力)，圖3(b)為輸油軟管組成粒子的蒙皮截圖，圖3(c)為輸油軟管的仿真效果。

圖3 海上補給裝備輸油軟管彎曲效應視景仿真效果Fig. 3 Visual simulation results of the bending effect of the oil hose of the replenishment equipment

2.2.3 海上補給裝備柔性體長距離附著約束的設置與計算

海上補給裝備柔性體通常存在自由端，且自由端會附著輸油軟管、貨物、掛鉤等設備，此時柔性體會隨著附著物的運動而出現擺動。在使用PBD方法對上述存在附著物時柔性體的模擬中發現，若將附著物看作柔性體的末端節點進行迭代計算時，則容易產生附著物被一同拉升而出現彈性失真。長距離附著約束只計算從附著物與柔性體接觸點粒子到柔性體自由粒子的整個路徑的拉伸，不對附著物產生影響[15]。

海上干貨補給是在高架索上設置行車，行車下部通過4 根吊帶懸掛貨物小車。4 根吊帶屬于柔性體，且作業過程中呈拉伸狀態，而下部懸吊的貨物小車屬于剛體，在行車運行時，貨物小車會出現擺動。若將貨物小車與吊帶看作一個整體進行柔性體仿真，則施加拉伸約束后，貨物小車也會出現拉伸變形。因此，需要在貨物小車與吊帶之間添加長距離附著約束，從而實現具有附著物的吊帶自由端在貨物小車重力作用下自由擺動時不出現貨物小車的變形失真。仿真效果如圖4 所示。

圖4 吊掛索具與吊筐之間的擺動效應的視景 仿真效果Fig. 4 Visual simulation results of the swing effect between the hanging rigging and the hanging basket

2.2.4 海上補給裝備柔性體與附著物相互約束的設置與計算

海上補給裝備柔性體端部一般都會連接附著物，如發射引纜。發射引纜是海上航行橫向補給作業的第一步，目的是便于接收艦通過引纜接收高架索等索具。引纜是一根纖維軟繩，前段掛有引纜球，通過撇纜槍發射到接收艦。發射引纜時，引纜隨撇纜球到達接收艦的過程中，柔性體和附著物都可以進行3 自由度運動，且相互影響。為模擬柔性體與附著物相互作用，本文通過銷子、銷接頭等引腳約束連接多個物體，引腳約束可以確保這些物體在每一個時間步長更新的位置與所連接物體的附著點位置一致。使用單邊引腳約束，以確保物體頂點位于動態物體的外部，從而避免了物體之間穿透現象的產生。仿真效果如圖5 所示。

圖5 引纜與撇纜球之間的相互作用效應的視景 仿真效果Fig. 5 Visual simulation results of the interaction effect between the lead cable and the mooring ball

2.3 海上補給仿真訓練時效性計算

在確定PBD 算法后，還需確定仿真迭代計算方法，用于確保在較少的迭代步數下，模型計算盡快收斂。PBD 算法通常采用非線性高斯-賽德爾或牛頓迭代法兩種迭代算法進行計算。本文通過以下算例比較非線性高斯-賽德爾或牛頓迭代法兩種迭代算法，確定海上補給柔性體仿真中迭代算法。

海上補給仿真訓練系統將柔性體分段長度設為0.2 m，重力加速度為9.8 m/s2，比較非線性高斯-賽德爾迭代和牛頓迭代梁總算法的相對誤差與迭代次數[16]，發現迭代次數相同的情況下，高斯-賽德爾迭代法在收斂速度上優于牛頓法，如表1 所示，采用兩種不同的方法計算得到不同的迭代次數下所用的時間和對應的相對誤差。從表1 中可以看出，在 5 次迭代計算時，PBD 方法得到的相對誤差為9.02×10-3、耗時為28 ms，而牛頓迭代法得到的相對誤差為4.5×10-2、耗時為422 ms。兩種方法在5 次迭代內均已經能夠滿足仿真精度的需求，牛頓迭代算法更加耗時。因此，本文采用的高斯-賽德爾迭代方法在較低的迭代次數時能較好地滿足仿真系統的要求，且表現出更好的穩定性能。從仿真實時性的角度考慮，此方法在交互應用中更具有優勢。

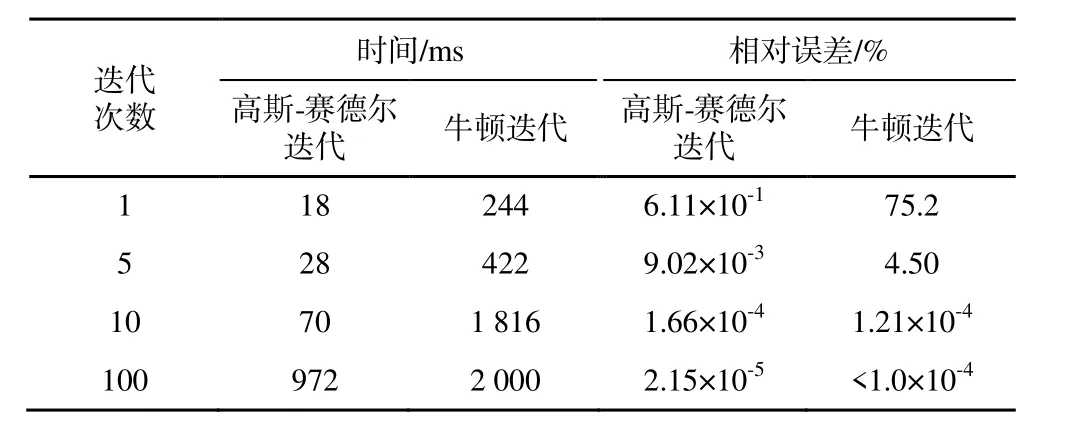
表1 PBD 方法的性能結果Table 1 Performance results of the PBD method

2.4 海上補給仿真訓練系統

本文從多體動力學模型出發，建立補給裝備索具柔性體模型，并運用PBD 算法開展海上補給裝備索具視景仿真研究，使用了拉伸約束、彎曲約束、長距離附著物約束和單邊引腳約束，避免了變形失真。通過提高索具、輸油軟管等柔性體的動態逼真度，復現海上補給實際狀態，并以此為基礎研發了海上補給仿真訓練系統，用于開展海上航行橫向干、液貨補給仿真訓練[17-20]。

該系統為國內首套用于海上補給訓練的仿真系統，可開展海上航行橫向補給全流程訓練。通過部隊試用，反映出本文系統索具、輸油軟管等柔性體的動態逼真度極高，能夠很好地復現海上補給實際狀態，訓練效果基本與實裝訓練一致，可有效提升海軍部隊海上補給的訓練水平。

3 結論

本文針對海上補給仿真訓練系統尚存在柔性體變形失真的問題，建立海上補給裝備索具柔性體多體動力學仿真模型，通過增加拉伸約束、彎曲約束、長距離約束和附著物相互約束實現了柔性體的動態變形三維模擬。最后通過比較高斯-賽德爾與牛頓算法的實時計算效果，確定本文采用的高斯-賽德爾迭代方法來提高視景仿真的效果，避免因為計算時間長導致畫面失真。最終開發出了海上補給仿真訓練系統，極大地提高了系統的操作真實感，為海上補給專業官兵盡快形成戰斗力提供了有效途徑。