新型四足并聯軍用機器人步態控制算法及仿真

李姍姍 , 王洪波 , 陳建宇 , 張興超 , 田俊杰 , 牛建業

(1. 燕山大學 河北省并聯機器人與機電系統實驗室，河北 秦皇島 066004; 2. 燕山大學 先進鍛壓成形技術與科學教育部重點實驗室，河北 秦皇島 066004; 3. 復旦大學 工程與應用技術研究院，上海 200433)

0 引言

軍用機器人是用于軍事戰場的特種機器人，在21 世紀的科技化戰場上，軍用機器人有著非常廣泛的應用場景，小到物資運輸大到實戰進攻勘探都能看到它們的身影。軍用機器人的出現和應用，改變了傳統軍隊的作戰方式，促進了現代軍事防御的發展。由于軍事戰場的環境一般都比較惡劣，涉及山地斜坡類的崎嶇不平路面，這就對機器人的移動控制提出了更高的要求。

四足機器人移動控制系統為一個非線性控制系統，擁有傳感器的多輸入到電機的多輸出結構，此系統能通過不連續且復雜的動力學計算完成機器人不同工作模式與外界環境的實時切換[1]，實現機器人的快速響應。

目前常用的控制方法有3 種，第1 種為根據零力矩點的多用于控制雙足機器人的動態穩定步態[2]算法，其缺點是會造成機器人運行的不穩定性和運動速度緩慢；第2 種是基于有節奏運動生物的中央模式(CPG)的模仿控制方法，即控制機器人的關節是通過多個相互耦合的非線性振蕩器輸出信號來實現的，其優點是機器人能具有良好的運行穩定性和越障能力[3-5]；最后一種是由Raibert 提出的虛擬模型控制框架方法，即機器人足端運動軌跡的控制是通過直接輸入機器人規劃好的運動狀態(方向、姿態、速度)進行這些物理直覺來實現的，是一種用來描述交互作用力解耦的控制方法[6-9]，此方法在控制過程中能很大程度地簡化對計算動力學模型的需求，同時也很大程度地提高了機器人硬件上的響應速度。其次，機器人的各種運動狀態參數此方法都可穩定快速地直接進行調整，即使受到外界沖擊和干擾時機體也可以快速恢復穩定。

本文針對四足機器人步態提出一種新型控制算法，由CPG 生成機器人行走時的基礎步態，完成輸入輸出之間的非線性振蕩器模型搭建，在對虛擬模型進行融合的基礎上計算出用于調整機器人姿態的力矩，并借助靜力學平衡映射為能夠對機器人行走進行控制的關節輸出。此方法在簡化控制網絡的同時還能保證機器人在行走過程中擁有較強的靈活性和抗干擾能力。

1 四足并聯軍用機器人整機構型介紹

機器人整機機構如圖1 所示，機體上安裝有 4 條獨立且對稱的機械腿，將為機器人運動供電的儲蓄電池、驅動器和腿部電機安裝在機體上，此外還可裝載需要運送的貨物。

機器人機械腿用3-UPS 機構作為單腿基礎結構，在行走過程中機器人的機械腿此時具有6 個自由度，其機構如圖2 所示，主要由上基座、支撐和足底組成，結構比較緊湊，可在腿部關節處安裝驅動電機和減速器，同時單腿機構也能具有更強的負載能力。機器人主體通過連接板與單腿機構相連，由伺服電機驅動的電動滑臺也與連接板相連，且呈120°按圓周均勻分布，借助彈性聯軸器絲杠的一端與伺服電機相連，另一端又與滑臺相連，伺服電機帶動絲杠旋轉，從而實現了對滑臺的移動控制。單腿機構中的滑臺即為3-UPS 機構中的3 個P 副，可實現機器人單腿機構運動參數和機器人四足間距的調整，使機器人在復雜路況下的越障能力和適應能力都得到了很大提高。

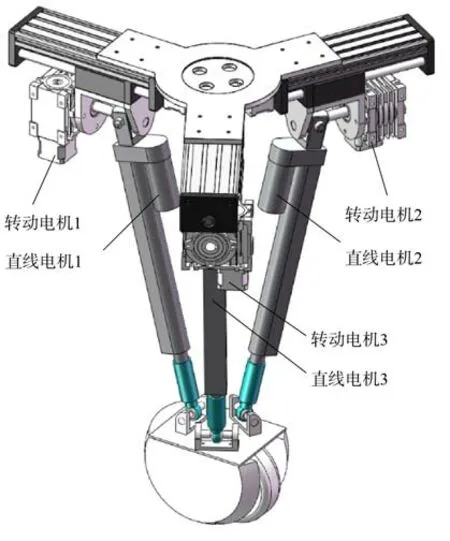
圖2 單腿機構Fig. 2 One leg mechanism

在機構零件圖3 中，機器人的腿部機構由3 個直線驅動副支撐，一端與U 副次軸連接，另一端通過魚眼軸承和軸承支架安裝在足底上。基座部分滑臺下端連接主軸支架，與伺服電機固連的型號為NRV030 蝸輪蝸桿減速器與主軸支架相連。U 副主軸一端與減速器相連接，另一端與支架相連，U 副主軸上安裝有套筒，圖中的U 副次軸由套筒和螺栓構成，其中驅動軸為U 副主軸。因此機器人單腿3-UPS 機構中6 個自由度的驅動動力源是由單腿機構中3 個直線驅動副和3 個驅動U 副主軸的電機來提供的。

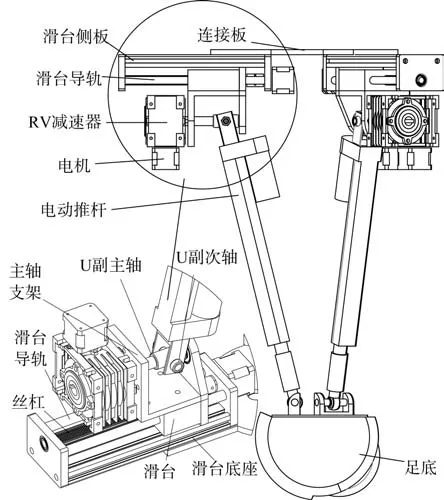
圖3 機器人單腿的結構圖Fig. 3 Diagram of a single leg of the robot

2 四足移動機器人的虛擬步態控制

2.1 基于Kuramoto 模型的虛擬控制模式

針對這一復雜的四足移動機器人控制問題，本文中機器人的腿部末端采用延遲同步模型當作發生器，這樣在運動過程中機器人的各腿部機構能保證相互耦合，而便于控制的Kuramoto 模型屬于同步的振蕩器模型。在此基礎上，其能夠把一個協同系統從無序復雜狀態轉化成同步狀態的過程模擬出來。本文機器人的關節角度也以相互耦合的4 個Kuramoto 模型當作生成器，并把關節角映射成帶有滯后同步的步態時序。

當采用全耦合的方式讓單一振子與其他振子相互作用時，用wm表示第m個振子的自然頻率，其動力學模型表示為

式中：θm為關節運動的相位，θm隨振子每循環一個周期就變化2π；k為振子間相互耦合強度；N為振蕩器的數量；θ˙m為振子的頻率。當k= 0時，表明各振蕩器間互相獨立，這時各振子用θ˙m=wm表示其自身的動力學模型，并且每個振子互不影響。

以w為自然頻率的獨立非線性振蕩器，要使其每個振子相互影響，則其耦合系數不能為0。調查結果表明當w滿足柯西分布時，N趨于無窮，耦合強度會趨于一個臨界值，當其高于此臨界值時系統的全部頻率均會收斂一致，此時系統變為同步 振動[10]。用一個圓對系統中所有的振子進行描述，且求和平均后，則系統同步的程度即為其值在復平面內質心處矢量的模，用式(2)表示為

式中：i 為虛數單位。式(2)也稱復序參量，簡稱序參量。這里矢量的方向用負指數定義，序參量的取值范圍為0 到1，且其值的大小與系統的同步程度有關，值越大則系統的同步程度也越高。即當系統的振子越分散、耦合系數越低時，序參量的值越接近0；當系統的振子耦合系數越高時，序參量的值越接近1，此時序參數較高，系統處于部分同步狀態，但仍不能到達單位圓上[11-13]；當系統的序參量為1 時，此時系統處于完全同步的理想狀態。由以上分析知系統振子從相互獨立到部分相關再到完全同步的狀態，是系統中各個相互作用的振子克服了固有頻率的結果。

設x為隨機變量，將歐拉公式sinx= (eix- e-ix)/(2i)和式(2)代入式(1)，可以得到：

式中：R為復序參量的模；ψ為任意相位。

本文中的機器人在運動時4 條腿都擁有相同的運動軌跡，只是各條腿之間有個固定的相位差存在，因此要對處于同步狀態的Kuramoto 模型做出一定的調整，確保系統中各振蕩器在周期震蕩時所輸出的相位差是固定的。為便于描述各振蕩器的相位遲滯或阻挫，現定義φmn為相位差，表示振子n與m間的相位差，并代入式(1)。又因在實際工況中系統中的電機都是以2π 為周期，故對自然頻率wm做出更改，令其為2πp(p為自然頻率)，再對耦合系數進行更改，令wnm=k/N。則此時的KM 模型為

1.2 虛擬控制的振蕩器網絡搭建與步態參數映射

本文研究的機器人4 條腿是對稱分布，每條腿對應各自的振蕩器模型，機器人在行走時各腿部驅動關節處的相位是呈現規律性變化關系的，此時各腿的振蕩器模型完成輸出和每個驅動關節的映射關系。又因在Kuramoto 模型中θm的輸出量是一條直線，且單調遞增，并不適用于機器人的關節控制和驅動。故本文振蕩器網絡需要引入正弦函數來對其輸出進行調整。

本文四足移動軍用機器人單腿機構為3-UPS機構，其控制網絡結構如圖4 所示，從中可知控制網絡中振子間均設計為雙向對稱形式，故振子間耦合強度均為wnm=wmn=1，同時相位差均為φmn=-φnm= π/12。

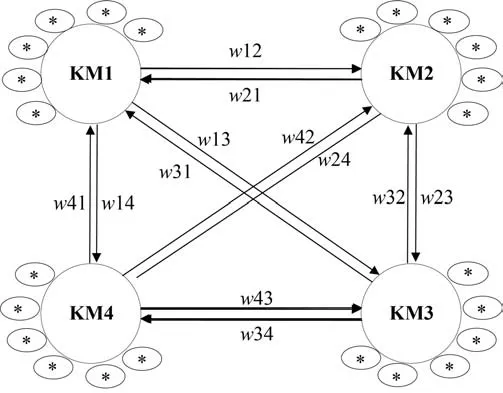
圖4 非線性振子耦合網絡Fig. 4 Coupled nonlinear oscillator network

單腿機構的簡單控制網絡完成搭建后，就要對KM 模型的主要參數進行分析確定，完成其輸出的角度映射。以右前腿向右的步進運動為例，對其進行分解并投影，如圖5 所示。圖5 中，S為步長，Am、Lm分別表示腿部的轉動電機幅值和推桿電機長度均處于最大值，Bm為腿部的次長分支轉動電機幅值，L、h分別表示腿部足端距髖關節和離地最高高度。

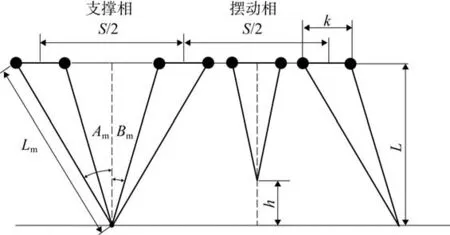
圖5 單腿周期行走圖Fig. 5 Diagram of periodic walking of a single leg

當機器人的支撐相為右前腿時，這時腿部的轉動電機幅值和推桿電機長度均處于最大值處，分別用Lm和Am表示，機體依靠關節電機的驅動使機體前移S/2，然后右前腿離地成為擺動相，其他腿觸地成支撐相。由機器人的腿部結構分析可知，只有當機器人側向邁腿時，上平臺的驅動電機才會轉動，向前邁腿時是不轉動的，腿部關節電機幅值的投影才是其幅值Am。圖6 所示為實際關節角度圖。圖6 中，單腿各分支在水平軸的投影用a表示；旋轉軸與水平面的夾角為60°，用α表示。則幅值Amax的實際值為

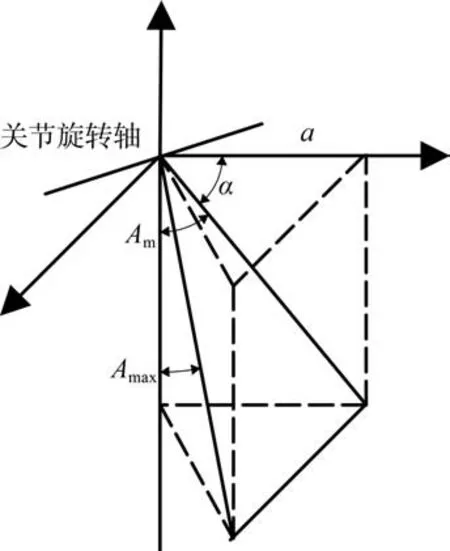
圖6 實際關節角度圖Fig. 6 Diagram of actual joint angle

再由腿部分解圖可以得出：

為使幅值對稱，選擇初始角度(Amax+Bmax)/2作為平衡點，則另外兩個腿部關節角度與驅動扭矩的關系式為

基于對機體腿部運動的研究發現，腿部的電動推桿的運動周期可劃分為兩個大運動周期，每個大運動周期包含一個小運動周期。當處于大周期內時，支撐相和擺動相運動的幅值不同；當處于小周期內時，伸縮桿的最短值相同，但最長值不同。

由圖5 知當其為支撐相時，令Lm為最長幅值，Lsm為次長值大小，則最小幅值為Ls=LmcosAmax，且腿部支撐相與擺動相相位差了半個周期。本文選定支撐相的初始長度設為(Lm+Ls)/2，則腿部各分支的長度表達式為

式中：T為運動周期。

當腿部處于擺動相時，其最低幅值變為Lmin=L-h，選擇初始長度為(Lm+Lmin)/2，則腿部各分支長度表達式和轉動電機表達式分別為

式中：f0(θ)為初始驅動扭矩值。

由此就可以確定取不同的步長和機體高度時的運動參數，可以用表1 和表2 將數據結果表示出來。

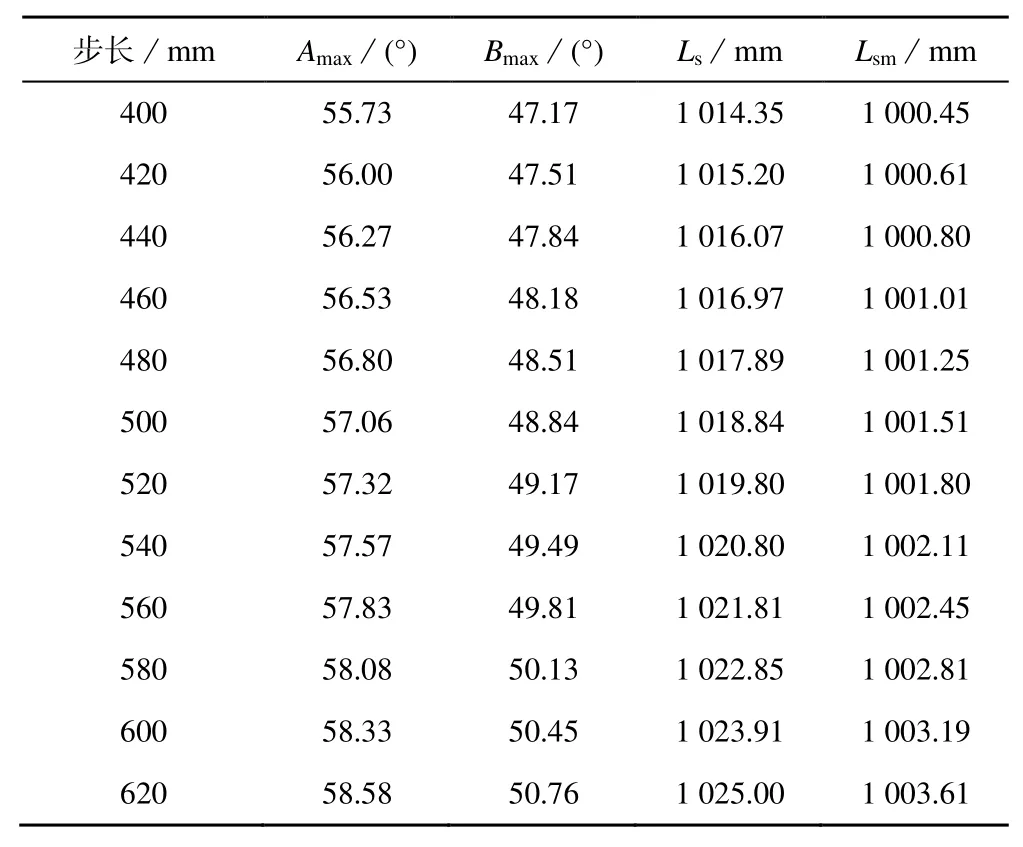
表1 步長與關節擺角關系Table 1 Relationship between step size and joint swing angle

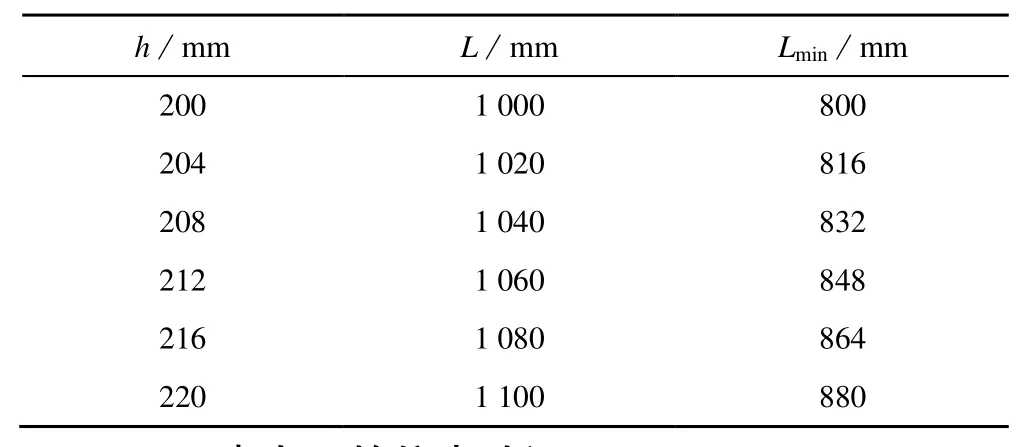
表2 抬腿高度與伸縮桿長度關系Table 2 Relationship between leg height and telescopic rod length

1.3 Trot 步態下的仿真驗證

通過觀察自然界中的四足動物可知，動物們的運動步態分 walk、trot、pace 和 gallop 4 種形 式[14-16]，且不管采用哪種運動步態行走，各腿之間均有著一定相位關系。本文把動物的各種步態運用到四足機器人上，并對這4種步態進行對比，發現比較常見的是trot 步態。故本文采用了對角腿相位相同的trot 步態，該步態會一直有2 條腿是支撐相，且與另外2條腿始終相隔半個周期，同時此種步態行走速度比較快，可用相位差矩陣表示出的步態時序為

本文令直線驅動電機Lmax= 1000 mm，Lmin= 500 mm 。小周期桿長為Lsm= 900 mm，步長選定540 mm，抬腿高度180 mm，耦合系數假定為500，以2 s 為周期，以0.1 為自然頻率，經計算行走速度為 0.27 m/s，Amax= 22°，Bmax=-11°，Ls=788 mm，Lmin= 622 mm。則trot 步態的KM 網絡表達式為

此時以trot 步態行走的機器人KM 物理模型就可由Simulink 軟件進行搭建，其整體框架如圖7所示，輸出結果如圖8、圖9 所示。

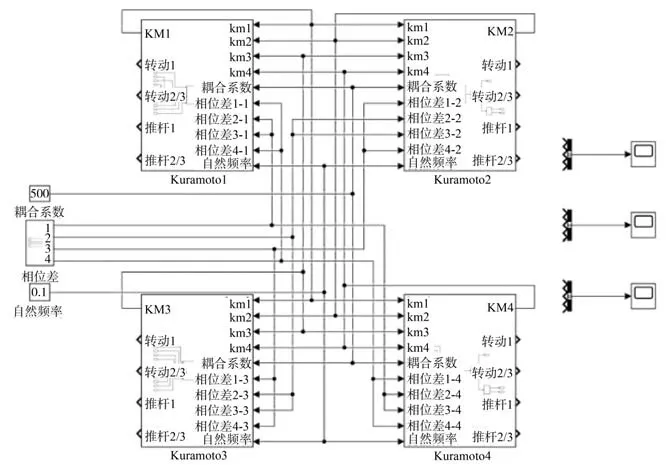
圖7 非線性振子耦合網絡圖Fig. 7 Diagram of coupled nonlinear oscillator network

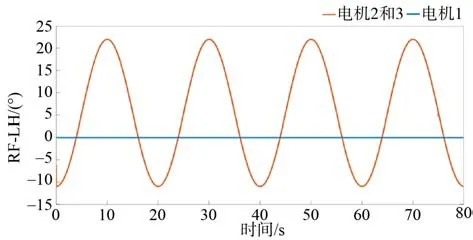
圖8 trot 步態轉動電機輸出曲線圖Fig. 8 Output curve of the trot motor

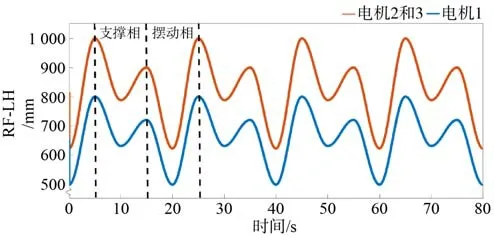
圖9 Trot 步態直線電機輸出曲線圖Fig. 9 Output curve of the trot linear motor

因為電機2 和電機3 關于電機1 對稱分布，所以電機 2 和電機 3 的輸出曲線是一致的。從 圖7~圖9 中可知，雖然機器人的耦合非線性KM網絡能很好地規劃出驅動電機的移動曲線，但在實際行走過程中卻把復雜的環境忽略了，會使機器人擁有較為僵硬的行走方式，這些會對機器人的機體和電機的使用壽命造成很大的損傷。為了讓機器人的運動更加柔順，就要在規劃電機曲線時把緩沖量加入到其與實際的電機控制中，從而確保在遇到復雜的路況時，機器人能更好的進行適應。

在實際中，可把四足動物的單腿關節進行簡化，當作一個彈簧阻尼器，同時提高阻尼系數以保證仿真結果的穩定性。本文機器人單腿將引入彈簧阻尼器來完成非線性KM 網絡的輸出量與扭矩的轉化，這樣就可以在控制機器人移動的同時，實現對機器人姿態的調整。但對于降低機器人因遇意外所產生的沖擊力，就需在各驅動關節角與期望值間虛擬增設彈簧阻尼模型，且此關節力矩控制也保障了機器人各關節的扭矩輸出。而關節的輸出力矩隨著足端期望角度的變化使得主動驅動關節隨期望關節角度對足端軌跡進行輸出。則此時機器人的腿部力矩輸出為

式中：Kqi、Bqi分別為跟隨的轉動關節彈性系數和阻尼系數；φqd、φ˙qd分別為轉動關節期望的角度和角速度；分別為跟隨的轉動關節期望的角度和角速度；Kli、Bli分別為跟隨的直線驅動關節彈性系數和阻尼系數；分別為期望的直線驅動關節長度和速度。

3 基于虛擬模型控制的姿態調整

3.1 俯仰角調整

以搭建虛擬機械部件的方式來模擬機構同外界環境的交互運動為核心的虛擬模型控制就是對交互行為進行描述的模型，其僅依靠機器人當前狀態即關節角度和速度再加上虛擬組件的狀態就可實現對機器人行為的控制，通過阻尼器和彈簧等虛擬組件簡化機體結構并與外界環境建立交互，應用更為簡潔的操作步驟實現對機器人機體運動的有效控制。為預防機器人航向偏離預定方向、機體在對角軸上出現劇烈翻轉和機體出現過大的傾斜角度等情況的發生，就需對機器人的航向、姿態、對角軸等方面進行機體姿態調整。

本文四足機器人能夠實現在自身坐標系中的 3 個轉動和3 個平動共6 個自由度的運動，為能全方位對機器人進行控制，需要充分研究機體的平動和轉動情況。但因存在于模型中的虛擬力在現實中是不存在的，故機器人是依靠腿部驅動關節來實現機體的運動。而將足端的力映射為各驅動關節工作空間的關節驅動力矩，需要用到各驅動關節的速度雅可比矩陣，其表達式為

式中：θ1~θ6分別為機器人腿部各驅動關節的速度；v為機器人腿部線速度；w為機器人腿部角速度。

依虛功原理得各關節驅動力和足端驅動力各自所做虛功總和是相等的，即

式中：τ1~τ6分別為機器人腿部各關節的驅動力；Fp為機器人的足端虛擬力。

將式(16)與式(17)聯立，得各關節驅動力與足端虛擬力的關系式為

機器人在運動時的俯仰角是通過調整機體繞側向軸的虛擬力矩來控制機體相對足端連線平面的傾斜角度。本文設定支撐相的足端連線與機體質心所構成的平面為機體標準面，并將機體軀干面通過彈簧阻尼虛擬組件與其進行相連，且定義機體標準面與軀干面的夾角為相對俯仰角φy，通過測量計算彈簧組件被壓縮或拉伸的大小來反映機體的傾斜程度。當機體繞質心發生轉動使機體軀干傾斜時，這時俯仰角φy和由虛擬彈簧模型產生的虛擬力都會發生改變，因此機體的后支撐相分配來的足端虛擬接觸力也會發生改變，就會對機體的俯仰角進行調整，最終會使機體與機體標準面相平行，如圖10所示。圖10 中，x軸表示機體前進方向，z軸表示機體豎直向上方向，xF、zF分別為豎直方向上前支撐相與后支撐相的坐標，xH、zH分別為x軸方向上前支撐相與后支撐相的坐標。

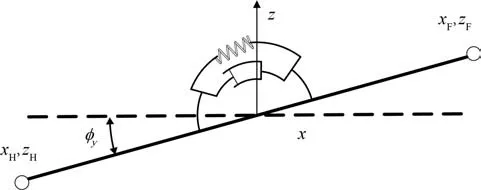
圖10 機體俯仰角調整圖Fig. 10 Diagram of pitch angle adjustment of the body

機器人機體俯仰角公式：

當機器人遇崎嶇路況時，會要求機體平面與標準面之間保持一定角度不變，因此由軀干質心處的彈簧阻尼模型通過相對俯仰角的變化而在機體側向軸上生成的虛擬力矩Ty為

式中：Kφy、Bφy為彈簧阻尼模型的彈性系數和阻尼系數；φyd為機體相對俯仰角期望值。但在實際情況下，機器人機體一般都要與足端連線相平行，此時虛擬力矩Ty為

3.2 對角軸翻滾

關于應用小跑步態的四足機器人的很多研究表明，機器人機體會繞對角支撐相發生轉動是由于在髖關節處生成的反作用力矩影響的。遇到這種情況時，機體的兩對角擺動相會有一個提前著地，這種異常著地雖會被耦合非線性振子網絡進行糾正，但此時的反作用力矩無法保證機體trot 步態的穩定性，且過大的足端著地沖擊力會在一定程度上損壞相應的電機，同時還會加重機體失穩的情況，甚至會使機器人的可靠性受到嚴重影響。

通過研究發現使機器人發生翻轉的主要原因有兩個，一個是因為機器人在向前行走時的兩支撐相會使機體繞髖關節處生成力矩，如圖11 所示，對此力矩在對角軸方向和與對角軸垂直的方向上進行分解，其中在質心處兩沿對角軸方向的合力矩會造成機器人沿對角軸發生翻轉的情況發生，翻轉方向可由右手定則的母指指向確定。另一個是因為移動的機器人會在機體質心處繞對角支撐相產生一定的傾覆力矩，此部分力矩可被慣性力矩平衡掉，或者采用某種方法消除掉，如姿態調整和附加重量的方法。由此可知兩個原因中前者對機器人的穩定運行產生的影響最大。

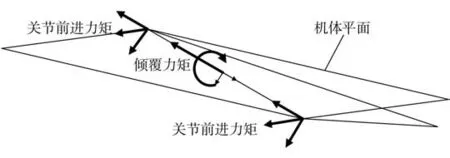
圖11 傾覆力矩圖Fig. 11 Overturning moment diagram

由KM 模型輸出的曲線可知，在機器人前進的過程中，位于髖關節處的側向轉動電機是不發揮功能的，其最主要功能是通過改變機體腿部與豎直方向的夾角使機器人更大程度地適應不同傾斜程度的地面，當機器人向前運動時其輸出的力矩可抵消掉引起機體傾覆的這部分關節輸出力矩，以提高機器人的防側翻能力。因而機器人是借助由彈簧阻尼模型生成的虛擬力矩來對變化的橫滾角進行修正，如圖12 所示。

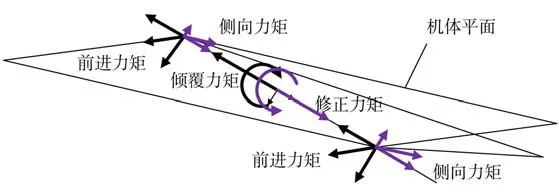
圖12 修正力矩圖Fig. 12 Corrected moment diagram

本文中機器人通過在機構中安裝陀螺儀的方法來達到隨時糾正機體繞對角軸傾斜的目的，當機體移動時用陀螺儀采集機體繞軸的角速度和角加速度，最后由虛擬彈簧阻尼模型輸出的虛擬力矩對傾覆力矩進行修正。通常對機體橫滾角的期望值為零，此時的虛擬力矩為

式中：Kφx、Bφx為彈簧阻尼模型的彈性系數和阻尼系數；φx為機體橫滾角期望值。

3.3 方向控制

要保證機器人能始終不改變預定的運動方向，就要實時對機器人在航向的偏差量進行調整。本文機器人腿部機構的自由度為6，因此在機器人的行進過程中機體可借助兩支撐相的足端反方向的側向接觸力實現對機體質心處繞z軸扭矩的調整，即對機體前進方向的調整是依靠支撐相反方向的虛擬力生成的側向速度實現的。依然使用虛擬彈簧阻尼模型對偏航角進行糾正，則式(23)為在機器人機體質心處生成的控制虛擬力矩的表達式：

式中：Kφz、Bφz為彈簧阻尼模型的彈性系數和阻尼系數；φzd為轉動關節期望的角度；φz為機體偏航角期望值。

當在機器人的行進過程中機體出現偏移量φz時，兩支撐相的足端反方向的側向虛擬力可實現對機體質心處繞z軸扭矩的調整來糾正機體的偏移量。然后機體隨φz的變化實時調整足端位移和側向速度來使機體轉動，保證機器人按預定的方向運動。但當機器人受到側向沖擊時，虛擬模型會在短暫的時間內調整前進方向，且在側向速度降低時回到正確方向。

3.4 高度調整與斜坡適應

當機器人在斜坡上行走時，其重心在豎直方向上的投影都會落在后支撐相周圍，此時由于重力的影響，機體會出現“后仰”現象，此時機體后支撐相將承擔其全部重力，而前支撐相會因與斜坡摩擦力不足出現打滑現象，更嚴重時會出現前支撐相直接離地的現象，如圖13(a)所示。為預防此種情況，本文采用姿態傳感器隨時對機體重心位置進行調整，保證機體重力在前后支撐相上的分配更均衡。故在斜坡上運動時，要使機器人的足端著地點在髖關節的坐標原點處有偏移量產生，讓其重心在豎直方向上的投影都能落在后支撐相著地點周圍，使前后支撐相所承擔的重力差變小，讓機體的穩定性盡可能得到提高，調整過程如圖13所示。圖13中，θ為機體軀干與斜坡的夾角，y軸為機體前進方向，z軸為垂直于機體豎直向上，Dy為足端落地點相對于髖關節坐標原點的偏移量。

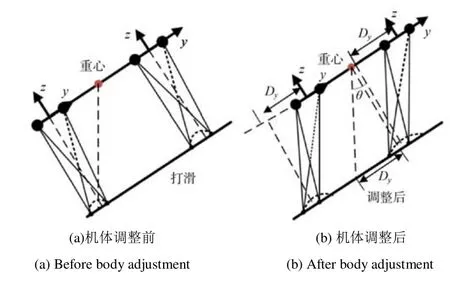
圖13 修正力矩圖Fig. 13 Corrected moment diagram

首先要借助支撐相對預期的機體高度實施調整，而機器人兩支撐相的髖關節高度的平均值就是機體的高度值。這里依然需要借助彈簧阻尼模型來完成針對機體腿部高度的調整，而在豎直方向上對機體速度的期望值通常為零，此時的虛擬力為

式中：Kh、Bh為彈簧阻尼模型的彈性系數和阻尼系數；hzd為轉動關節在豎直方向上的期望高度。

對機體的偏移完成修正后，這時支撐相高度的平均值就是機器人質心的高度值，以小跑步態為例也就是兩支撐相的平均高度，則預期的支撐相足端偏移量表達式為

式中：Y為支撐相足端實際偏移量。

當機器人在斜坡上運動時，機器人經由足端預期落地點和實際落地點間的偏移來對機器人重心進行調整，讓其始終在支撐相中心處附近，這樣使得機器人的爬坡穩定性會增加，還能在一定程度上預防足端打滑現象的發生。由增益控制器對足端偏移量進行映射，得到可以對其進行調整的力矩，則此時的修正力矩為

式中：Kx為增益控制器的調整系數。

4 四足移動軍用機器人整機步態控制規劃

4.1 虛擬力的分配

本文中機器人控制機體實現設定的預期運動狀態的虛擬力是由虛擬彈簧阻尼模型產生的，然而這些虛擬力是如何使機體單腿分支上的主動驅動關節執行出來需要進一步研究。由于機器人各腿足端的虛擬力不相同，在主動關節處產生的驅動力矩也不同，因此需要一種虛擬力的分配機制將控制機體運動狀態的虛擬力分配到不同腿上由此映射出這些虛擬力所需要的關節力矩。目前對這些虛擬力進行平均分配到機器人四條腿的足端處是最簡單的方法，但由于處在動態行走中的機器人是欠驅動的，例如使用trot 步態的機器人在移動時同時只有兩腿著地，這時虛擬力的分配就不再是簡單的四等分了。而本文中對應用trot 步態的機器人足端虛擬力的調配問題借助了靜力學分析法進行確定，其中機體的各虛擬力如圖14 所示。圖14 中，fF,x、fF,y、fF,z為前肢足端虛擬力在3 個坐標軸上的分量，fH,x、fH,y、fH,z為后肢足端虛擬力在3 個坐標軸上的分量。

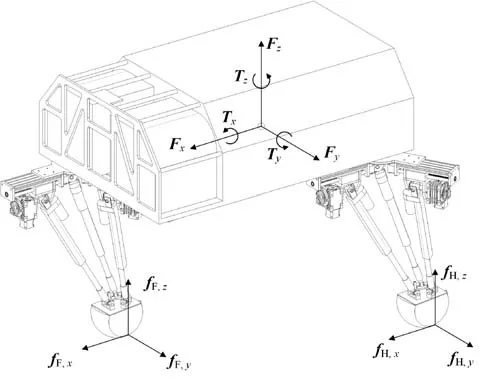
圖14 非線性振子耦合網絡圖Fig. 14 Diagram of coupled nonlinear oscillator network

首先對處于trot 步態的機器人進行整體受力分析，設機體每條腿的重力都作用于其靜態平臺中心處，四條腿的重力和即為機體所受的合力，然后把合力分解為沿垂直方向向下的機體重力GB與4 條腿相同的簡化重力Gi(i=1、2、3、4)5 個部分。再將這五部分力在各自坐標系中沿坐標軸進行分解，但因相同的腿部簡化重力在機體質心處的和力矩為 0 N·m，為預防奇異矩陣的出現，本文將在機體運動方向上的3 個虛擬力也在其坐標系中標出。則作用在機體質心處的虛擬力矩與虛擬力的求解表達式為

式中：Gx、Gy、Gz為機體重力在x、y、z軸上的分量；xH、yH、zH為機體支撐相后足端虛擬力在x、y、z軸上的分量；xF、yF、zF為機體支撐相前足端虛擬力在x、y、z軸上的分量。當機器人運動時，一般都會令其橫滾角φx=0，這樣在y軸方向上的機器人機體重力會為0 N，但受俯仰角yφ的影響，則在x、y、z軸方向上機器人的重力大小分 別為

式中：M為機器人質量；g為重力加速度。則支撐相的足端虛擬力可由式(28)求出，再將式(28)改寫為矩陣形式，有

觀察式(29)的系數矩陣可發現，其秩為5 而非滿秩，這表明僅靠機器人支撐相的足端虛擬力是實現不了機器人機體全方位運動控制的，要想實現機器人的全方位控制就得先限制機器人的某些運動狀態控制，然后再對機器人的虛擬力進行求解。而對自然界中四足動物的觀察還可發現，當其目的地在其身體側面的某一位置時，動物們并不會直接進行側向移動，而是先旋轉自身方向再進行移動，所以本文認為側向移動對機器人來說作用不大，故選擇側向虛擬力Fy進行限制，針對Fy添加約束條件fF,y=fH,y后，式(29)變為

觀察式(30)可發現其系數矩陣不為0，其必存在逆矩陣，則對式(30)的系數矩陣求逆再與機體控制虛擬力相乘可得機器人各腿足端點的虛擬力。而事實上本文機器人已用非線性振蕩器網絡得出了其向前運動時所需的主動驅動力矩，并沒有用到機體質心處的虛擬力，只是將控制機器人姿態的虛擬扭矩和控制機身高度的虛擬力進行了映射，故選取系數矩陣的逆矩陣中虛擬扭矩所對應的后5 列即可。但當處于行走中的機器人受到側向沖擊時，機器人的增益控制器就會為縮短響應時間直接輸出與側向沖擊力速度有關的足端虛擬力fF,y=fH,y=ky·vy/2 (ky為增益控制器的調整系數)，此時足端虛擬力為

式中：qij(i=1, ···, 5,j=1,···, 6)為系數矩陣的第i行第j列的元素。

確定了機器人各腿的足端虛擬力后，再借助虛功原理把它反映成主動驅動力矩，則控制機體姿態的單腿驅動力矩：

式中：Q表示系數矩陣。

進一步，此方法也可應用到機器人支撐相為多足時的步態算法中。

4.2 整體步態控制

本文中基于Kuramoto 非線性振蕩器的中央模式控制生成四足機器人運動所需的基礎信息，關節力矩則由彈簧阻尼模型生成。考慮到處于運動狀態的機器人需要對其自身姿態、著地角度和運動方向的調整，本文采用虛擬組件對處于運動狀態的腿部各關節交互力的偏差量實時檢測，通過虛擬模型控制計算出修正偏差，由其校正因處于不同步態時非線性振子產生的各關節輸出量，其整體控制框如 圖15 所示。

由圖15 可知，先是由KM 控制網絡產生步態控制信息，再經彈簧阻尼模型輸出為各關節力矩，由其控制機器人擺動腿的運動軌跡和時序。機器人也會隨時把支撐相的各姿態信息向姿態控制器發送，機器人再經虛擬模型算出調整機體姿態所需的虛擬力，對其分配就能得到控制機器人姿態的各關節力矩，這些力矩和由KM 控制網絡生成力矩一起對機器人的運動進行控制。

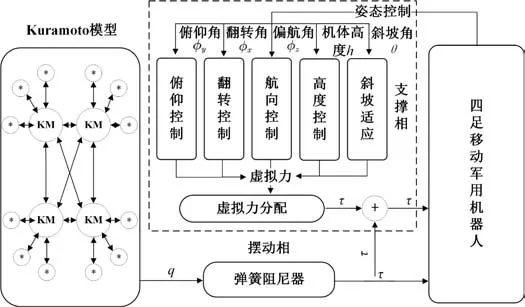
圖15 步態規劃整體框圖Fig. 15 Overall block diagram of gait planning

5 控制算法虛擬仿真驗證

5.1 V-REP 中虛擬樣機搭建

基于第3、4 節的研究，下面就軍用機器人的步態控制算法進行驗證，看其能否穩定且有效地對機器人的運動進行控制。首先將本文中機器人的虛擬樣機模型在V-REP 軟件中完成搭建，并把驗證移動控制算法所需要的仿真環境建好，通過仿真軟件監測本文中機器人處于不同運動狀態時的各種數據以及關于穩定裕度的變化，再由分析得到的各種數據來判斷此控制算法能否穩定且有效的對機器人進行控制[17-20]。

四足移動軍用機器人的三維模型已經在SolidWorks 軟件中設計完成，而要想在V-REP 中實現對三維模型的仿真，就需要在V-REP 軟件中按照實體–關節–實體的順序重新構建一個帶有各構件間依賴關系的機器人虛擬模型，最終模型如圖16所示。

圖16 最終模型圖Fig. 16 Final model drawing

最后，為測得機器人各足端的接觸力和機器人在移動過程中的姿態角，還需在模型各足端處和模型中心處均加上傳感器。

5.2 步態控制算法驗證

為簡化仿真操作，本文利用MATLAB 軟件Simulink 中的控制模型直接控制V-REP 中的虛擬樣機。本文采用Simulink 軟件中Function 直接調用V-REP 中的remoteAPI 連接庫同外部程序進行通訊[21-22]，即步態控制模型在Simulink 中就完成了搭建，再由Simulink 與V-REP 通信以達到控制V-REP 中的虛擬模型運動對其步態控制策略進行驗正的目的，則整體模型框架如圖17 所示。

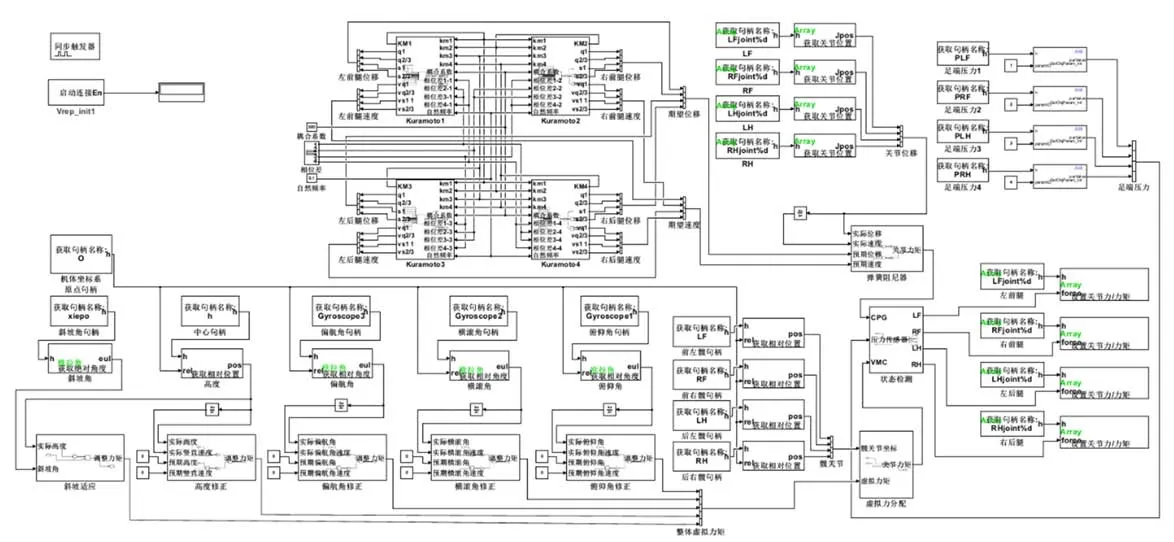
圖17 步態控制模型Fig. 17 Gait control model

由圖17 可知，步態控制模型的左上角連接VREP，啟動時由 V-REP 計算的數據會實時向MATLAB 中發送；KM 中央模型發生器位于模型上半部分，其功能為計算出機器人行走時的各關節位移，并由彈簧阻尼器將其映射成關節扭矩后再輸出；模型的下半部分用來對機器人的行走狀態進行控制，由位于V-REP 中的傳感器把采集到的數據返回到MATLAB 軟件，由虛擬模型計算出機器人保持預期狀態所需要的虛擬力矩，然后把控制各關節進行調整的力矩經由靜力學平衡進行分配，再把中央模型發生器產生的力矩和狀態檢測得到的支撐相力矩結合，最后對實時傳入V-REP 中由模型計算出的力矩進行仿真。

5.3 平坦路面行走仿真驗證

首先要對處于正常行走狀態的機器人應用步態控制算法測出其各項運動參數。然后對在V-REP 中虛擬樣機應用在MATLAB 軟件中搭建的步態控制算法進行平坦地面行走仿真，如圖18 所示。此時在trot 步態下機器人的前進速度為0.5 m/s，由圖18 可知位于機器人機體上對角線方位的機械腿動作是一致的，相互交替使機器人平穩向前運動，且在仿真過程中未出現使機器人機體震顫或摔倒的情況。

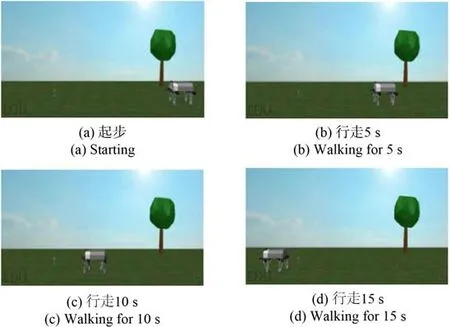
圖18 平地實驗Fig. 18 Ground experiment

為保證機器人能夠穩定的運行，V-REP 需要把機體姿態角隨時向位于MATLAB 軟件中的步態控制器發送，保證實時輸出足端虛擬力。當機器人處于行走狀態時，機體的各個姿態角和高度的檢測值變化情況如圖19 所示。

由圖19 可知，機器人機體的姿態角均存在誤差，且為周期性的，都是因為在步行狀態中機器人抬腿、落腿等動作生成的難以回避的誤差，但誤差值均在-1°~1°之間；由圖19(d)可知，機身高度的誤差最小。因此可知本文機器人能保證機體按照規劃好的航向和身體姿態穩定的進行運動，機體速度和足端沖擊力如圖20 所示。

圖19 機體姿態與高度Fig. 19 Body attitude and altitude

由圖20(a)可知，機體前進速度會隨機器人的運動狀態發生變化，在最開始的幾秒內，機器人由靜止狀態到快步提速然后速度趨于穩定；由 圖20(b)可知，因機器人足端不停的在觸地-分離間轉換，會使機體側向速度產生很小的瞬時誤差； 由圖20(c)可知，機體豎直方向速度會因周期性出現的左前足端沖擊力的影響產生最大0.05 m/s左右的誤差，可忽略不計。由此可得本文機器人在行走過程中能保證機體的平穩，不會使機體發生速度突變和機身傾斜的情況。

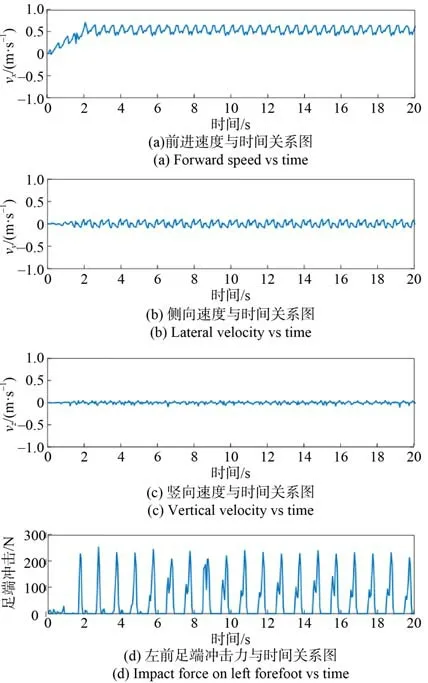
圖20 機體速度與足端力Fig. 20 Body speed and foot force

5.4 斜坡行走仿真驗證

下面對處于斜坡行走的機器人進行適應能力驗證。首先在實驗環境中設立一個傾角為6°的斜坡，然后對邁入斜坡和在斜坡上運動時機器人的各項運動參數進行觀察，仿真結果如圖21 所示。

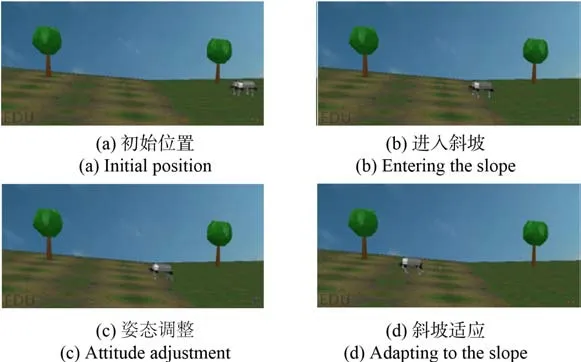
圖21 斜坡實驗Fig. 21 Slope experiment

當機器人邁入斜坡時，機體各個姿態角和高度的檢測值變化情況如圖22 所示。

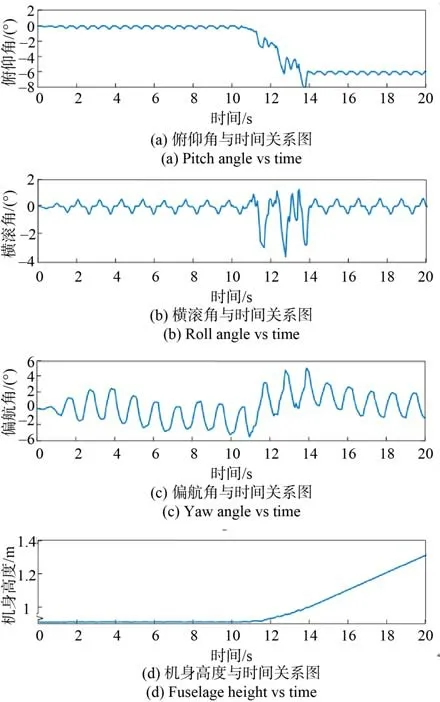
圖22 機體姿態與高度Fig. 22 Body attitude and altitude

從圖22中可知，機身的俯仰角會在機器人邁入斜坡時發生驟降，擔當機器人全部機身邁入斜坡后，機身的俯仰角會穩定在與斜坡傾角相同的6°左右，達到新的平衡狀態。由圖22(c)得知，機身的行走的趨勢因不確定的足端接觸力會向左側傾斜，隨后又因虛擬力的作用機體又會向右產生傾斜，最終機體會沿原定角度行走；由圖22(d)可知，在爬坡過程中機器人機體始終保持穩定的移動狀態。機器人速度曲線如圖23所示。

從圖23中得知：除在剛踏入斜坡時機體速度會產生不穩定變化外，都能保證機體速度的平穩，但由于斜坡的影響，在豎直方向機體會產生一個穩定且不在為0 m/s的速度；除在剛踏入斜坡時機器人因步態調整產生了較大的接觸力外，都能保證機體的平穩運行。

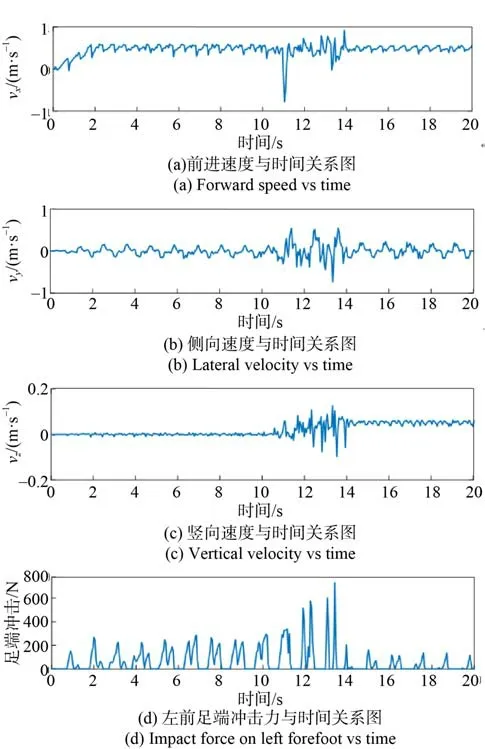
圖23 機體速度與足端力Fig. 23 Body speed and foot force

5.5 側向沖擊仿真驗證

四足機器人在行走過程中，由于機身長度一般大于機身寬度，故機體在受到側面沖擊時會產生更大的顛覆力矩。本文擬用鐘擺錘模擬機身側面的沖擊力來測試機器人的穩定性，鐘擺錘重40 kg，擺繩長0.6 m，初始角度為60°，則發生撞擊時速度為2.5 m/s，沖量為100 kg·m/s。當機器人的速度與姿態角受沖擊而失去穩定性時，由控制器中虛擬模型計算出用來恢復機體平衡所需的足端虛擬力，實驗過程如圖24所示。

圖24 沖擊實驗Fig. 24 Impact test

當機器人遭受側向沖擊力作用時，機體各個姿態角和高度的檢測值變化情況如圖25所示。

從圖25(a)中得知，機身的俯仰角會驟降同時機體后仰，但因誤差的存在，這時由虛擬模型生成的足端虛擬力可使機體向后仰的趨勢減弱，并最后使機體慢慢恢復平衡狀態。從圖25(b)中得知，機身橫滾角因沖擊力的影響瞬時產生一個反向偏角，且與機身前進方向一致，用來對開始側移的機身進行修正，并最終恢復到原來的穩定狀態。從 圖25(c)中得知，因本文假設沖擊力作用于機器人的前半身處，故在行進方向上機器人偏航角的瞬時偏差最大能達20°左右，會與原前進方向產生偏離，但隨機體足端虛擬力對偏航角的調整，最終機器人的行進方向又恢復原方向上。其速度曲線如 圖26所示。

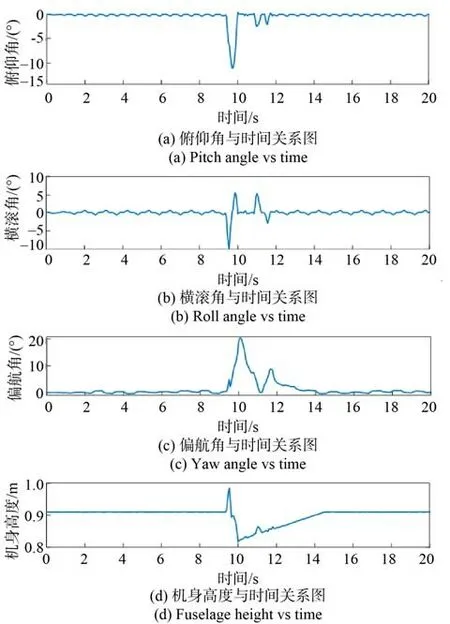
圖25 機體姿態與高度Fig. 25 Body attitude and altitude

從圖26(a)中得知，機器人的前進速度因沖擊的影響發生驟降，但隨機體腿部姿態的調整，最終機器人的行進速度恢復到原來的穩定狀態。由于機體受到的沖擊來自側面，故圖26(b)中的速度值變化最明顯，突變峰值可達2 m/s，此時機器人因與預期速度產生偏離，機體會通過持續對足端虛擬力進行調整來糾正機體的側向速度，一定時間后側向速度會趨于0 m/s，機體恢復到正常狀態。從 圖26(c)和圖26(d)中可知，豎向速度的劇變同姿態角相同，機體剛受到沖擊力時就會瞬時后仰，此時速度發生突變，然后隨著機體姿態的不斷調整速度也在不斷變化，并最終恢復到正常狀態。

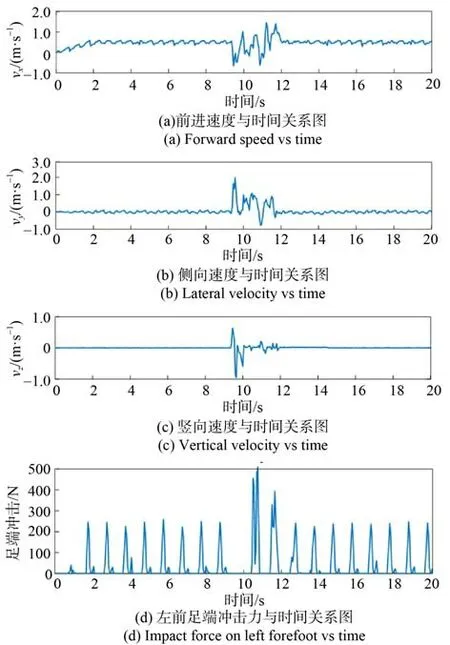
圖26 機體速度與足端力Fig. 26 Body speed and foot force

6 結論

本文在四足移動軍用機器人控制上把基于CPG 的控制方法和基于虛擬模型的控制方法進行綜合，為四足軍用機器人的步態行走控制設計了一種新型控制模式，在V-REP 軟件中搭建出虛擬樣機，在Simulink 軟件中搭建出步態控制算法的框架，通過V-REP 與MATLAB 軟件對該虛擬樣機步態進行聯合實驗仿真。仿真結果驗證了這種步態控制算法的有效性，在簡化控制網絡的同時還能保證機器人在行走過程中擁有較強的靈活性和抗干擾能力，這種新型控制模式也為四足并聯軍用機器人的步態控制提供了新的思路與方法。