基床系數對基礎設計的影響
姜斐斐,梁志剛,劉振民
(1.杭州市建筑設計研究院有限公司,浙江 杭州 310008;2.義烏城市投資建設集團有限公司,浙江 義烏 322000)
0 引言
在基礎設計中,當有限元計算模型采用彈性地基梁板法時,基于文克爾假定,用線性彈簧來模擬樁土的支撐作用。將樁土對基礎的支撐作用用線性彈簧來模擬,土彈簧剛度取基床系數與梁板單元底面積的乘積,樁彈簧剛度根據樁體材料確定。采用有限元方法計算筏板基礎的變形和內力,同時采用分層總和法進行沉降計算,調整基礎剛度使基礎變形和沉降趨于一致,從而實現上部結構、基礎與地基土共同作用。因此,基床系數和樁剛度的取值對樁和基礎設計非常重要。樁剛度可根據《建筑樁基技術規范》附錄C規定進行計算[1],本文主要針對基床系數對基礎設計的影響作討論。
1 基床系數對基礎設計的影響
基床系數是指地基土在外力作用下產生單位變形時需要的壓力,如式(1)所示。
影響基床系數的因素很多,如土的類別,土的物理力學性質,結構物基礎大小、形狀、剛度、位移,基礎埋深,應力水平,應力狀態,地下水狀態,時間效應等,其中土的類別、含水量、稠度狀態,密實程度時土體本身對壓縮變形影響最大的因素[2-3]。確定基床系數的方法也很多,包括原位測試方法、室內土工試驗方法和經驗公式法[4-5]。
為研究基床系數對基礎設計的影響,采用盈建科軟件建立地上10層地下一層的框架結構,采用樁筏基礎如圖1所示,樁徑700mm,筏板厚度600mm。

圖1 樁筏基礎
設定樁豎向剛度為100000kN/m,比較不同基床系數取值時的樁土荷載分擔情況。分別取基床系數為5000~10000kN/m3時,筏板下基底反力和樁豎向反力分布如圖2至圖9所示。

圖2 基底反力分布(K=5000)

圖3 基底反力分布(K=10000)

圖4 基底反力分布(K=50000)

圖5 基底反力分布(K=100000)

圖6 樁豎向反力分布(K=5000)
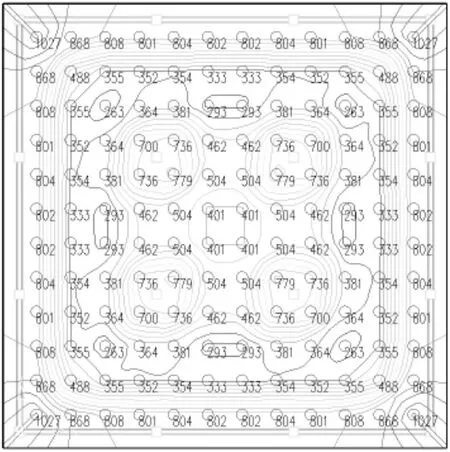
圖7 樁豎向反力分布(K=10000)

圖8 樁豎向反力分布(K=50000)

圖9 樁豎向反力分布(K=100000)
隨著基床系數增大,基底反力逐漸增大,樁反力相應減小,樁土承載力分擔比逐步下降。同時,基床系數增大,表明土的剛度增加,抵抗變形能力增加,基礎總體變形量減小,基礎變形越來越集中在框架柱范圍內,相應基底反力也逐漸向框架柱范圍內集中。比較不同基床系數取值下,底板基底反力和樁反力分布與基床系數的關系如圖10所示。
由圖10可知,隨著基床系數增大,基底反力標準差逐漸增大,表明其分布越來越不均勻;樁反力標準差逐漸減小,表明其分布越來越趨于均勻。因此,在土質較差的地基土上設計樁筏基礎時,樁反力離散性較大,基床系數雖然較均勻,但是其分擔比例較小,考慮樁土共同作用并不經濟。當基床系數較大時,樁反力和基底反力的離散性都較小,考慮樁土共同作用進行樁基設計是比較經濟合理的。
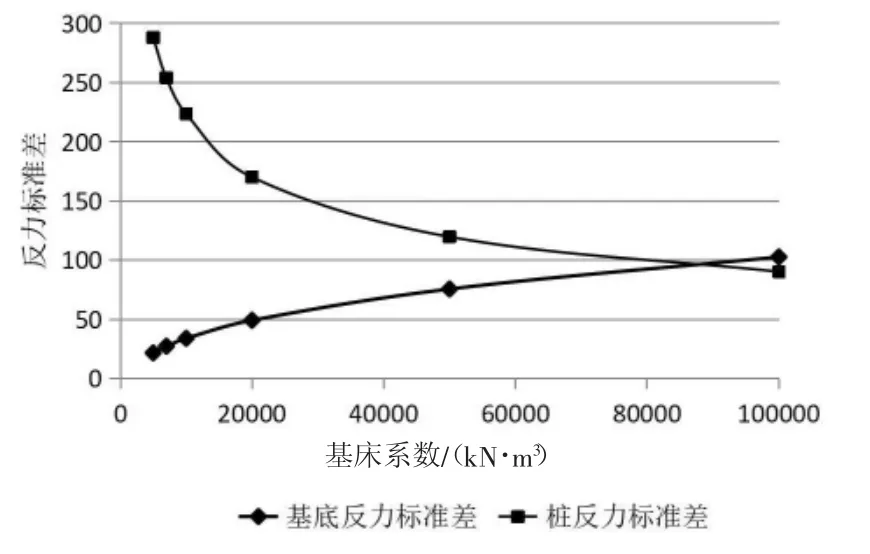
圖10 基底反力、樁反力標準差與基床系數的關系
2 樁土承載力分擔比估算
為了考察基床系數對樁土承載力分擔比的影響,分別建立地上10層,地下1層的框架結構和地上20層,地下1層的框架結構,調整基床系數與單位面積樁剛度之間的比值,樁土承載力的比值變化情況如圖11所示。
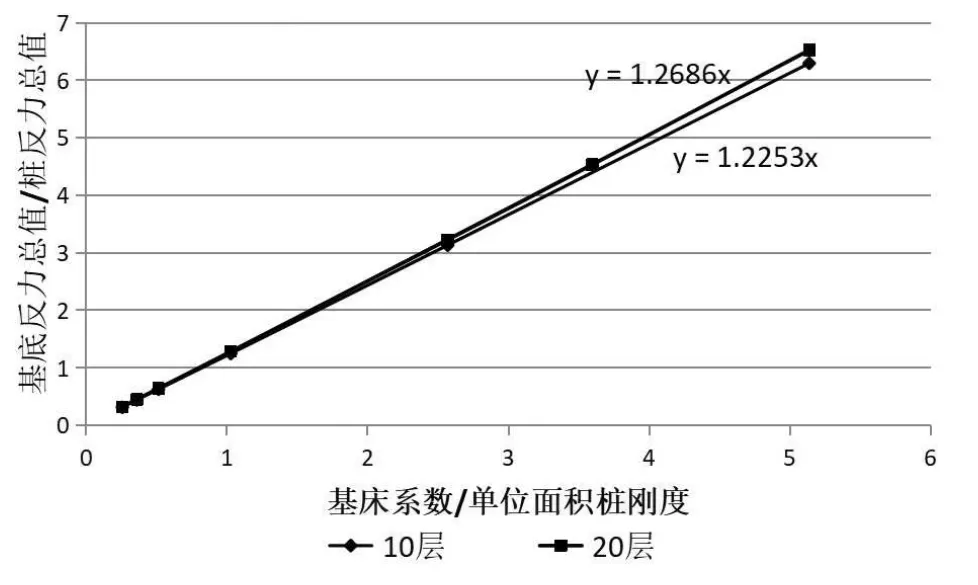
圖11 不同層數框架結構地基反力對比
對地上20層,地下1層框架結構,樁剛度取值變化時,調整基床系數與單位面積樁剛度之間的比值,樁土承載力的比值變化情況如圖12所示。

圖12 不同樁剛度下地基反力對比
可以看出,在一定的布樁密度情況下,基底反力與樁反力的比值和基床系數與單位面積樁剛度的比值基本成線性關系。比例系數受上部荷載大小、樁剛度取值的影響不大。這是因為根據彈性地基梁法的文克爾地基假定,樁土的支撐作用都是用線性彈簧來模擬的,所以在反力分配上呈現一定的線性比例關系。不同布樁密度時地基反力的對比如圖13所示。

圖13 不同布樁密度時地基反力對比
隨著布樁密度的變化,基底反力與樁反力的比值和基床系數與單位面積樁剛度的比值之間的線性比例隨之發生變化。布樁密度越大,比例系數越大。在本算例中,該比例系數與單位面積樁數之間也近似存在線性關系,如圖14所示。
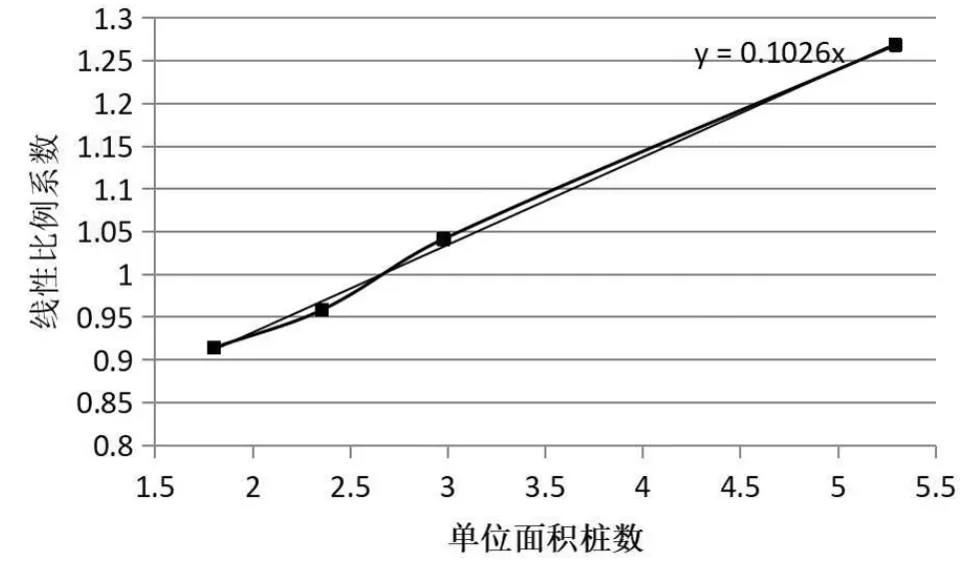
圖14 比例系數與單位面積樁數的關系
因此,當基床系數和單位面積樁剛度確定時,可以根據以上線性關系求得樁土承載力分擔比。反過來,當基床系數和樁剛度取值確定時,考慮充分發揮地基承載力和單樁承載力,則可以根據此時基底反力與樁反力的比值求得單位面積樁剛度,即最優的樁數量。
3 結語
基床系數越大,基底反力分布越不均勻;樁反力分布越趨于均勻。
基床系數較小時,考慮樁土共同作用并不經濟。基床系數較大時,考慮樁土共同作用進行樁基設計是比較經濟合理的。
在一定的布樁密度情況下,基底反力與樁反力的比值和基床系數與單位面積樁剛度的比值基本成線性關系。其比例系數受上部荷載大小、樁剛度取值的影響不大。
基底反力與樁反力的比值和基床系數與單位面積樁剛度的比值之間的線性比例隨布樁密度變化發生變化。

