具有緊急制動功能的多模式自適應巡航控制策略
歐 健,黃 棟,林嘉玉,楊鄂川,韓先勝
(1.重慶理工大學 車輛工程學院, 重慶 400054;2.重慶工貿職業技術學院 車輛工程學院, 重慶 408000;3.重慶理工大學 機械工程學院, 重慶 400054)
近年來,汽車的保有量逐年增加,據國家公安部統計[1],截至2021年底機動車保有量達3.95億輛。為了提高駕駛員的行車安全性和便捷性,全世界各汽車行業都在開發高級駕駛輔助系統(advanced driving assistance system,ADAS),特別是自適應巡航控制的研究與開發備受關注[2]。
ACC控制結構會影響到控制器運行的整體效率,通常采用分層設計,包括上、下層控制器[3-5],其中上層控制器將傳感器檢測到的車輛信息,通過合適的控制方法,輸出期望加速度;下層控制器則將上層的輸出轉化為節氣門開度(驅動轉矩)和制動壓力,從而達到控制目標。針對控制器控制算法,國內外研究人員都做了大量的研究。清華大學的李升波等[6]總結到,目前已有多種算法被用于設計上層控制器:PD反饋控制器、模型預測控制(model predictive control,MPC)、滑模控制(sliding mode control,SMC)、最優控制(linear quadratic regulator,LQR)、線性變參數、強化學習等。下層控制器的設計也是ACC系統中的重要環節。其中,動力總成、制動系統模型以及驅動/制動間的切換策略是主要研究方向。下層控制器模型主要使用逆模型對上層輸出量進行跟蹤控制[7-8],文獻[9-10]則采用基于閾值的驅動制動模式切換策略。在以上控制算法中,PID[11-12]、LQR[13-14]和MPC[15-16]算法在ACC系統中有著更為普及的研究與應用,然而,相較于傳統PID的結構簡單且魯棒性好的優點,MPC則具有預測功能以及動態響應好等優點,且在處理多約束多目標問題上具有較大優勢。
目前,合理的切換模式和切換策略對整個ACC系統的實現具有重要意義,但關于這方面的研究相對較少。合肥工業大學的孫曉文等[17]將ACC系統分為巡航速度控制和跟車距離控制2種模式,提出的控制策略能夠保證ACC車輛的行車安全,但在車距與車速模式之間切換時,加速度會在短時間內超出期望值,降低了舒適性;吉林大學的高振海等[18]根據自車的加速度將ACC分為巡航、穩態跟隨和瞬態跟隨模式,但并未充分考慮前車加速度變化對ACC系統的影響;清華大學的王建強等[19]基于零期望加速度曲線,將ACC分為定速巡航、車距保持、接近前車和超車模式,較好地解決了模式切換中的加速度突變問題,但超車模式隸屬于駕駛員操作,不應存在于系統自動駕駛模式中;南昌大學的劉明春等[20]將ACC劃分為5個控制模式,將跟車模式細分為加速接近、穩態跟車、減速接近與緊急跟車4個模式,但文中并未考慮前方緊急工況與駕駛員特性;中國科學院微電子研究所的章軍輝等[21]將ACC系統劃分出6種工作模式,同時采用模糊推理與加速度加權平均策略,以實現工作模式最佳匹配與平穩過渡,文中雖考慮了部分駕駛員心理,但采用固定時距會在一定程度上降低車輛對環境的適應性能;北京理工大學的裴曉飛[22]將ACC更加詳細地劃分為8個模式,在處理縱向前車急加速、急減速與緊急工況中,具有良好的性能,但跟車過程太過詳細,反而導致整體控制模式太過繁瑣,不利于系統的穩定。
針對現階段ACC系統切換模式較為簡單,且未考慮前方突現靜止物的復雜交通狀況,將ACC系統劃分3種主模式和4種子工況,采用分層控制策略設計ACC控制器,其中,定速巡航模式采用模糊PID進行設計,可根據環境變化動態調整PID參數;跟隨模式在充分考慮行駛過程中的跟車性、安全性以及舒適性等指標的前提下,采用MPC算法進行設計與優化;基于電機模型設計下層控制器,并選取最大輪缸壓力作為接管模式下的制動壓力。最后采用CarSim/Simulink進行聯合仿真,驗證所設計ACC系統的可行性。
1 ACC框架定義
根據前方車輛是否處于自車巡航間距范圍,并考慮到緊急工況,本文基于距離和TTC將ACC模式劃分為巡航、跟隨和接管3種,為提高該控制器對復雜多變環境的適應能力,通過引入指標參數TTC-1,將跟隨模式進一步劃分為4種子工況:加速、強減速、弱減速、穩態跟隨,并設計基于MPC的多目標ACC控制器;基于模糊PID設計定速巡航模式;通過仿真實驗選取特定輪缸壓力作為緊急制動壓力,用于設計接管模式;最后通過搭建下層控制器和仿真環境形成ACC框架,如圖1所示。

圖1 ACC總體框架示意圖
2 模式切換策略與劃分設計
切換條件直接影響到整個模型的運行流暢性與邏輯性。距離和TTC由于計算量低且能減少決策時間,而被用于切換判據。
2.1 安全距離設計
2.1.1巡航距離
當前方無車、距離過遠或者前方車輛駛出當前車道時,自車進入定速巡航模式。考慮到控制器對復雜工況的適應能力,選取車頭時距和自車車速動態計算巡航間距,公式如下:
S=Thvf+d0
(1)
式中:S為巡航間距;Th為車頭時距,一般取值范圍為5~8 s,設置6 s作為巡航時距;vf為自車速度;d0為最小固定車間距,設置5 m作為最小車間距。
2.1.2接管距離
當前車緊急減速或者前方車輛掉落的障礙物,且滿足切換條件時,自車進入接管模式,本車以設定最大制動輪缸壓力進行縱向制動避撞。為了減少計算量,基于制動過程搭建縱向安全距離模型,計算接管間距,因此可得縱向安全距離表達式:
S=Sf+d0-Sd
(2)
考慮到緊急工況,選取前車靜止與緊急制動2種工況進行分析。
1) 前車靜止工況。
當同一車道前方車輛靜止時,自車執行緊急制動,制動過程前車位移Sd=0,自車制動位移為Sf。安全距離模型公式如下:
S=Sf+d0=
(3)
式中:t1為加速度從0到amax所需時間;t2為車速從v0減到0所需時間;v0為自車初始速度;Jmax為車輛制動減速度梯度,取Jmax=21 m·s-3。
2) 前車緊急制動工況。
當同一車道前車緊急制動時,自車也執行緊急制動,以避免碰撞。緊急制動下安全距離公式為:
(4)

2.1.3跟隨距離
當車間距處于巡航間距和接管間距之間時,自車進入跟隨模式。考慮到前車速度變化會影響車頭時距,為了使車間距更加貼合實際工況,設計一種可方便預測的VTH策略,其表達式如下:
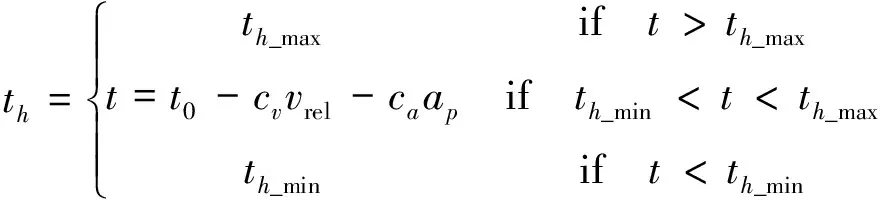
(5)
式中:th為車頭時距值;t0、cv為大于0的常數,其中t0=1.5 s,cv=0.05;vrel為兩車相對速度;th_max、th_min分別為車頭時距的上、下限值,其中,th_max=2.2,th_min=0.2;ca為大于0的常數,其中ca=0.3;ap為前車加速度。
結合可變車頭時距,可得期望跟車間距如下:
S=thv+d0
(6)
2.2 子模式劃分策略設計
跟隨模式主要針對安全距離下的穩態跟隨、加速、強減速、弱減速等工況,因此需對子工況進行劃分。基于TTC-1設計子模式,定義如下:
(7)
式中:Δv為兩車相對速度,Δv=v2-v1,v2為前車車速,v1為自車車速;d為兩車車間距。
當TTC-1接近0時,自車越安全,且穩態跟隨前車;當v2大于v1時,兩車越安全;反之,兩車容易發生碰撞。因此將子模式進行詳細的劃分:
1) 當-0.05≤TTC-1≤0.05時,車輛為穩態跟隨工況,加速度范圍為-0.6~0.6 m/s2;
2) 當-0.12≤TTC-1≤-0.05時,車輛為弱減速工況,最大減速度約束為-2 m/s2;
3) 當TTC-1≤-0.12時,車輛為強減速工況,最大減速度約束為-5 m/s2;
4) 當TTC-1≥0.05時,車輛為加速工況,加速度約束范圍為0.6~3.5 m/s2。
2.3 整體模式切換策略設計
在2.1節的基礎上,設計整體模式控制邏輯如圖2所示。
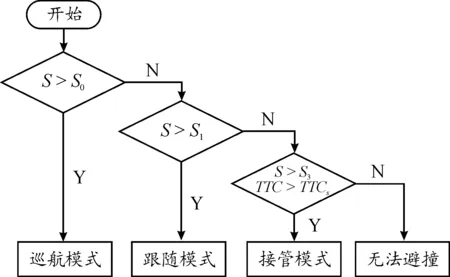
圖2 整體模式控制邏輯框圖
圖2中,S0、S1、S3以及TTCs分別為各種模式的切換條件,其中,定義S0為巡航間距,S1為接管間距,S3為無法避撞間距,TTCs=1.3 s[23],當滿足條件時,則進入對應模式,否則繼續保持模式不變,其工作流程如下:
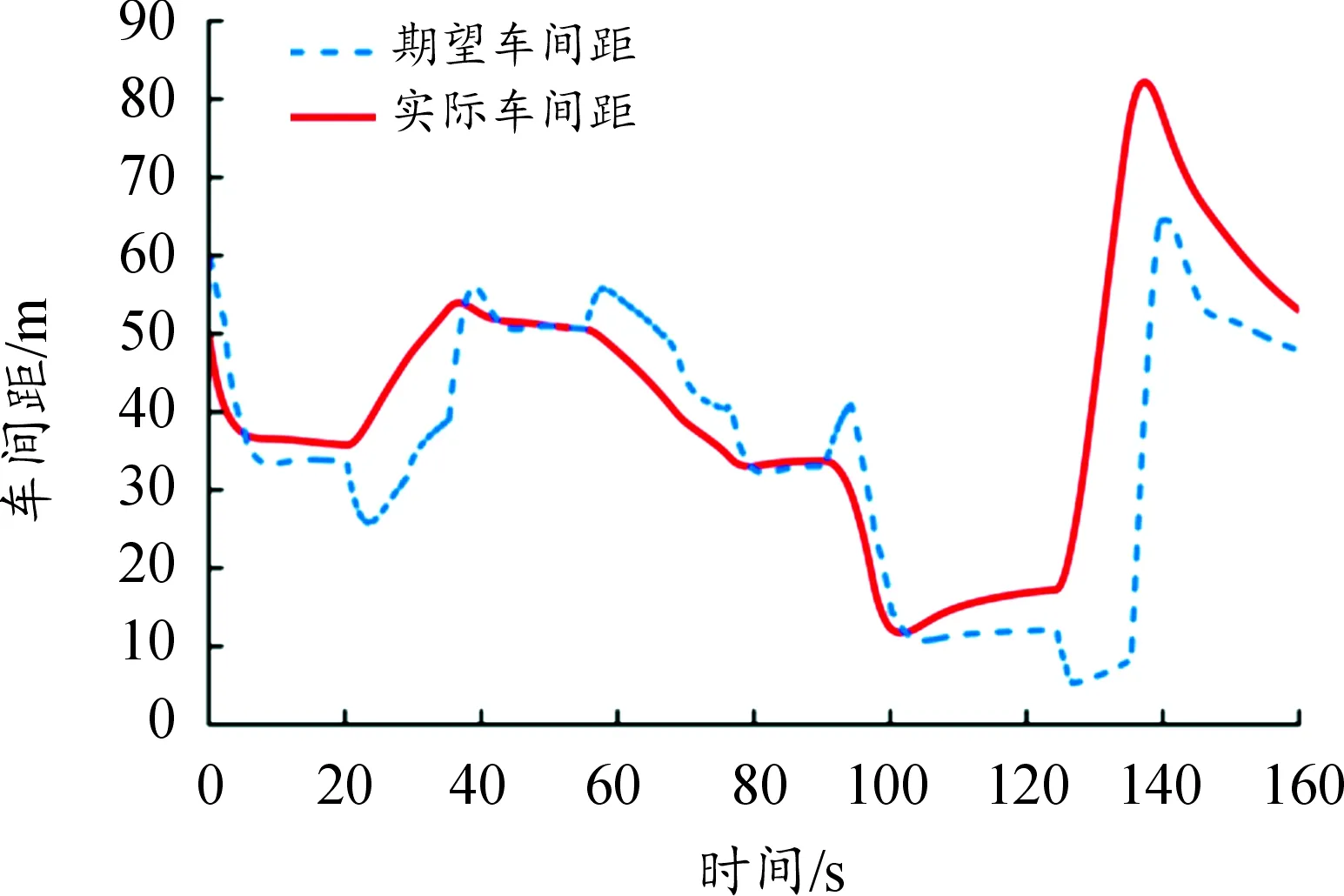
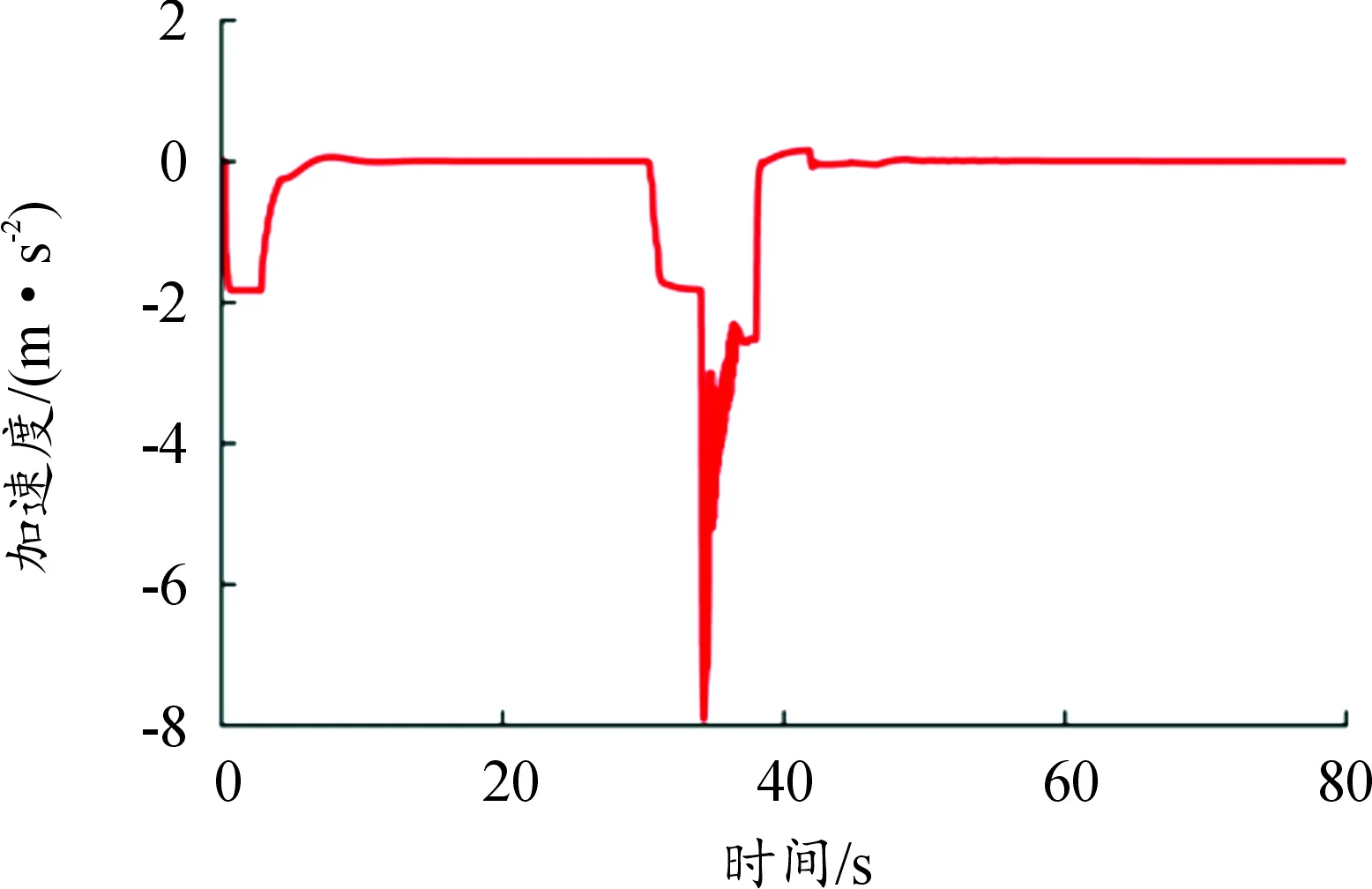
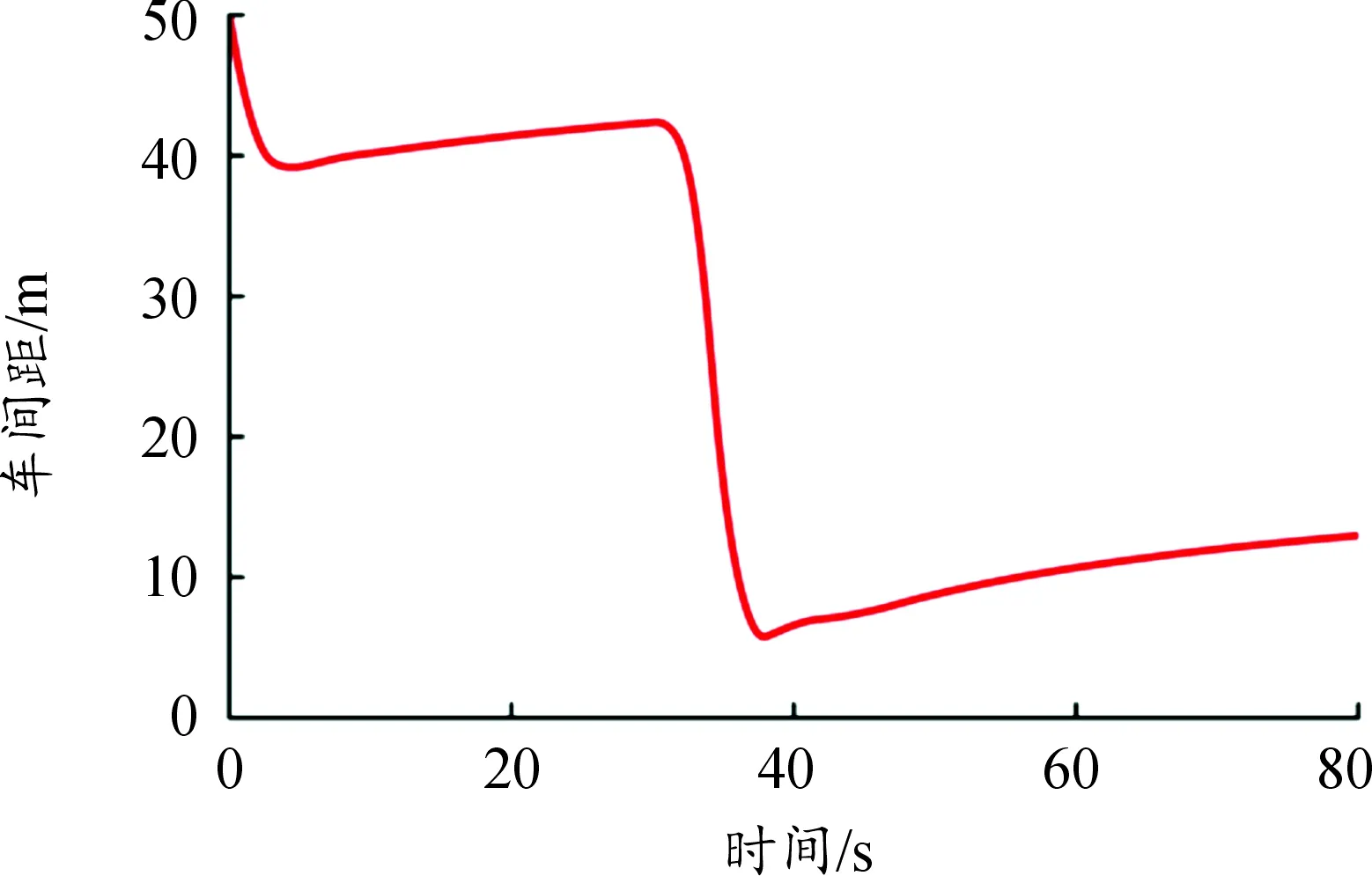
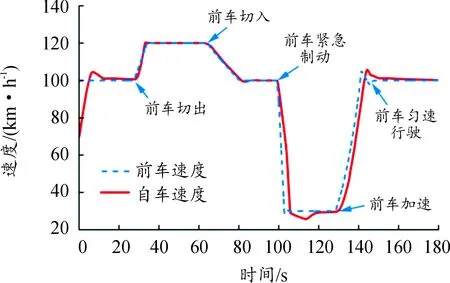
1) 當S0 2) 當S1 3) 當S3 3.1.1定速巡航模式設計 PID控制是通過輸入當前狀態值與設定值之間的誤差,計算變量輸出,其形式為: (8) 式中:u(t)為控制器的輸出變量;e(t)為當前值與設定值之間的誤差;kp、ki和kd分別為比例系數、積分系數和微分系數。 設定模糊PID控制器的輸入為當前速度與巡航速度的差值e,以及差值的變化率ec,輸出為車輛的期望加速度ades;E、Ec、Kp、Ki、Kd分別為e、ec、kp、ki、kd所對應的模糊值。定義e的基本論域為[-90,90],ec的基本論域為[-8.33,3.5];增益kp的基本論域為[1,10];增益ki的基本論域為[0.001,0.01];增益kd的基本論域為[0,2]。模糊變量均設定7個模糊集:負大(NB)、負中(NM)、負小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)。選用三角函數描述模糊輸入變量,如圖3所示,輸出變量與輸入變量隸屬度一致,不再贅述。 圖3 輸入變量隸屬度函數曲線 為保證曲線上升時間、超調量、穩定時間、穩態誤差合理,需調節增益Kp、Ki、Kd,最終建立模糊規則表,如表1所示,并在Matlab/Simulink中搭建量化因子與比例因子部分,從而控制車輛快速且舒適地跟蹤上巡航車速。 表1 Kp、Ki、Kd模糊推理規則 3.1.2跟隨模式設計 跟隨模式設計的好壞直接影響整體ACC控制器的性能表現,該模式主要功能是對復雜工況做出快速反應,同時兼顧多個優化目標,基于此,設計基于MPC的多目標ACC控制器。 1) 縱向動力學模型設計。 通過分析兩車間運動學關系,如圖4所示,考慮到自車加速度與加速度變化率,可得自車與前車的運動學公式如下: (9) 式中:Δx為實際車間距;ap為前車加速度;a為自車加速度;v為自車車速;vrel為相對車速;u為期望加速度;j為自車加速度變化率;Ts為采樣時間;τ為下層控制器控制時間。 圖4 兩車運動學關系示意圖 選取兩車車間距、自車車速、相對車速、自車加速度和自車加速度變化率作為ACC控制系統的狀態量[24],即x(k)= [Δx(k),v(k),vrel(k),a(k),j(k)]T。定義x為自車位置,選擇w作為系統干擾量,選取y(k)=[δ(k),vrel(k),a(k),j(k)]T作為待優化目標,整理得到縱向運動學狀態方程模型: (10) 式中: 式中,th為可變車頭時距。 文中引入指數衰減函數作為優化目標的參考軌跡,例如,兩車車間距的參考軌跡如下: δref(k+i)=δ(k)+ (11) 式中:δref為車間距誤差的參考軌跡;αδ為該參考軌跡的時間常數;同理,相對速度、自車加速度與自車加速度變化率設置同樣形式的參考軌跡,將參考軌跡用向量形式表示如下: 每個單元都要有明確目標,特別要突出能力目標。教師要把知識講授型為主變成知識應用型為主;從以理論思維為主,變成以能力訓練為主;從以知識點、定義、語法為載體,變成以完成項目任務為載體;從學生被動聽講,變成學生主動參與課堂,積極參與新知探索;從教師講解為主,變成由教師積極引導、創造學習的環境條件為主。把課程評價從 “老師講過”、“老師講得好”、“老師完成了教學進度”[2]為目的,變成以學生有興趣、學生的能力明顯提高為目的。老師精講知識,學生強練技能,在技能訓練過程中,學生自己學到了知識。 yrel(k+i)=φiy(k) (12) 式中:φ為車間距、相對速度、自車加速度與自車加速度變化率組成的對角矩陣;yrel為優化目標的參考軌跡向量。 2) 控制目的與約束分析。 通過控制兩車車間距保證兩車安全性,假定xp為前車位置,dc為最小安全間距,其安全性約束如下: xp(k)-x(k)≥dc (13) 車輛間的實際與期望車間距間的誤差應保證盡可能地小,且兩車在行駛過程中處于相對靜止狀態,其跟車性約束如下: δ(k)→0,vrel(k)→0 當k→∞ (14) 影響舒適性的主要因素是自車加速度以及加速度變化率jerk2個參數,因此,需要對其進行優化控制,其舒適性約束如下: (15) 此外,還需要對其他狀態量進行約束,使求解值在約束下達到最優,因此乘坐舒適性和燃油經濟性約束如下: (16) 3) 基于MPC的多目標ACC控制算法設計。 根據式(10),可建立預測時域內的預測方程,定義ex為實際狀態量與預測值之間的誤差;W(k+p)為p時域內的干擾量集合,且假定每一時刻值相等。整理得到表達式: (17) 增加權重參數Q和R,其中,Q代表跟車性,R代表安全性。整理得到如下函數表達式: (18) 式中:Q=diag(qδ,qv,qa,qj),u(k+i)為k+i采樣時刻的加速度控制值。 根據二次規劃(quadratic programming,QP)問題的求解規則,整理前述約束條件,得到如下形式: ΩU(k+n)≤T (19) 式中: 其中: 結合式(18)和(19),使用Matlab中積極求解器進行求解,輸出控制量序列,取輸出序列中的第一個控制量作為下層控制器的輸入。 本文采用輪轂電機作為動力源[25],因此,下層控制器便將上層控制器計算得到的期望加速度ades轉換為控制整車模型的驅動轉矩Tm與輪缸壓力Pb。 3.2.1輪轂電機模型 PMSM的數學模型是一個高度復雜的系統,為了使PMSM能更好地工作并施加相關控制,在做一定簡化與假設后,建立PMSM的數學模型如下: (20) 式中:Ld和Lq分別為d軸和q軸定子自感系數;id和iq分別為d軸和q軸定子電流;ud和uq分別為d軸和q軸定子端電壓;R為定子繞組電阻;ω為轉子的電子角速度;ψk為電機定子磁鏈;Te為電機扭矩;np為極對的數量;J為負載和機械轉子的慣性矩;Tl為負載扭矩;B為負載與機械的摩擦系數。 3.2.2車輛驅動模型 為簡化車輛行駛過程,在僅考慮縱向阻力下,通過對車輛受力分析,整理得到驅動力矩表達式為: (21) 式中:r為車輪滾動半徑;i0為主減速器傳動比;ηt為傳動系傳遞效率;CD為空氣阻力系數;A為汽車縱向受風面積;v為車速;m為整車質量;f為滾動阻力系數;θ為路面坡度;δ旋轉質量換算系數;ades為加速度。 3.2.3車輛制動模型 在制動過程,不考慮加速阻力和驅動力,且假定車輛在平路上行駛,整理可得縱向制動力Fb公式: (22) 在最大縱向制動力Fb約束范圍內,車輛的制動力Fb與油壓Pb呈線性變化,定義Kb為制動系數[26],Kb=1 286,其表達式如下: (23) 當前車緊急減速時,自車則需比其更大的減速度進行制動,以避免碰撞。在CarSim環境下,選取車速節點80、100、120 km/h作為測試初始車速,然后以特定輪缸壓力Pb進行制動,反向得到對應制動減速度ae,如表2所示。經分析對比,最后采用7 MPa作為緊急制動輪缸壓力。 表2 各車速、輪缸壓力下的制動減速度 3.2.4驅動/制動切換策略 在CarSim軟件中進行滑行實驗,得到各速度(10~120 km/h)下的加速度閾值a,為保證驅動/制動間的平穩切換,在原曲線基準的上下設置過渡區域Δh,設置Δh=0.1 m/s2,得到驅動/制動切換邏輯。 3.2.5下層控制器控制方法 本文采用簡單快捷的PID控制方案設計下層控制器,并在此基礎上引入前饋和誤差反饋的方式來彌補模型失配的不足,前饋即是通過上層控制器的計算輸出作用于ACC車輛的執行機構控制車輛,而誤差反饋則是通過實際狀態與期望狀態的偏差值進行調節,用來補償線性模型失配帶來的控制誤差,提升系統的控制精度,利用PID方法使得期望縱向加速度與實際縱向加速度的偏差值迅速收斂為0,實現對ACC車輛的高效控制,運用試湊法,設定PID控制器的控制參數為kp=0.2、ki=1.8。 為了對所設計的模式切換策略以及控制器進行驗證,搭建Matlab/Simulink與CarSim聯合仿真平臺,其仿真參數如表3所示。 表3 主要仿真參數 設置定速巡航、跟隨、緊急制動以及混合切換4種工況進行仿真驗證,并在CarSim中將前車駕駛設置為駕駛員操作,并應用于所有工況。 4.1.1定速巡航工況 車輛定速巡航時,ACC進入速度控制模式。車輛設置仿真環境如:自車初始車速為90 km/h,巡航車速為120 km/h,且當前車道無前方車輛,其仿真結果如圖5和圖6所示。 圖5 速度變化曲線 圖6 加速度變化曲線 從圖5中可以看出,當車輛進入巡航模式時,車輛能迅速響應控制器決策,大約在4.8 s時,車速從90 km/h加速至120 km/h,且速度超調量幾乎為0,其后車輛以當前設定巡航速度行駛;從圖6中可以看出,自車加速度在些許波動后能快速恢復穩定,保證了乘坐舒適性,同時表明控制器具有穩定性。 4.1.2跟隨工況 車輛跟隨前車行駛時,ACC進入距離控制模式。設置仿真環境如:本車的初始速度為90 km/h,且在0~160 s之間做加速、強減速、弱減速以及穩態行駛動作,兩車初始車間距為50 m。其仿真結果如圖7—9所示。 圖7 速度變化曲線 圖8 加速度變化曲線 圖9 車間距變化曲線 從圖7和圖9中可以看出,自車在各種子工況下都能很好地跟隨前車速度,且響應迅速,雖存在超調現象,但最終都能穩定跟隨前車行駛;在減速期間,自車與前車未發生碰撞,始終保持安全距離行駛;從圖8可以看出,自車實際加速度皆在子模式下的加速度約束范圍內,整個過程的加速度保持在-5~3.5 m/s2。 4.1.3前車緊急制動工況 當車輛面臨緊急工況時,切換至接管模式,ACC進入距離控制模式。設置仿真環境如:自車初始車速為120 km/h,前車初始車速為100 km/h,兩車初始車間距為50 m,當車輛行駛到30 s時,前車開始緊急制動約2.7 s,車速降至30 km/h。其仿真結果如圖10—12所示。 圖10 速度變化曲線 圖11 加速度變化曲線 圖12 車間距變化曲線 從圖10和圖11可以看出,在30 s時,前車開始緊急減速行駛,最大減速度為7.2 m/s2,為避免碰撞,自車切換至接管模式,并以7 MPa的制動輪缸壓力制動,最大減速度為7.9 m/s2,當控制器判斷為非緊急工況時,自車則切換至跟隨模式,且切換策略工作流暢,保證了乘員的舒適性;從圖12可以看出,在38 s時,兩車車間距為6 m,說明兩車在緊急工況下仍能保證安全。 4.1.4混合切換工況 為驗證所設計切換策略以及控制器,設置混合工況仿真環境如:自車初始車速為70 km/h,前車初始車速為100 km/h,兩車初始車間距為40 m;在29 s和63 s時,前車分別切出、切入當前車道,在99 s時,前車在2.7 s內緊急制動至 30 km/h,前車在其他時間段做加速、強減速、弱減速以及穩態行駛。其仿真結果如圖13—16所示。 圖13 速度變化曲線 圖14 加速度變化曲線 圖15 車間距變化曲線 圖16 Jerk變化曲線 從圖13和圖14可以看出,在整個仿真過程中,自車速度能很好地跟隨前車,且和加速度并未產生不正常突變;在緊急制動過程中,自車能快速反應,最大減速度達7.9 m/s2,在保證安全性的同時,亦能較快吻合前車速度,大部分時間段的減速度均能維持在-5~3.5 m/s2,保證了行駛舒適性;整體模式切換流程從跟隨模式至定速巡航模式至跟隨模式至接管模式至跟隨模式,模式間均能實現穩態切換;從圖15中可以看出,在行駛至99 s時,車輛開始緊急制動,最終兩車車間距能保持在5.6 m,且未與前車發生碰撞;從圖16中可以看出,除了緊急制動工況,其他工況下的jerk基本維持在-3~3 m/s3,再次體現了駕乘舒適性。 本文提出了一種具有緊急制動功能的多模式自適應巡航控制策略。針對目前復雜多變的工況,特別是緊急工況,將整體控制模式劃分為巡航、跟隨和接管3種模式,并將跟隨模式下的工況進行了更加詳細的劃分;同時,對3種模式進行了詳細設計;多種仿真工況結果表明,所設計的ACC控制器能快速且穩定地跟蹤前車速度或巡航速度,模糊PID控制下的速度幾乎無超調,MPC控制能保持在10 km/h以內,且迅速恢復穩定;除緊急工況,其他情況下的加速度均能保持在-5~3.5 m/s2;在緊急工況下,自車與前車最終能保持5.5 m左右的車間距,其他工況下的車間距可根據相對速度以及加速度參數動態調整;且所有控制模式可根據復雜多變的工況進行快速平穩切換。 所設計的ACC控制策略滿足跟隨性、安全性、舒適性以及適應性的要求,且切換模式有效平穩,在緊急工況下能通過縱向避撞策略實現緊急避撞。本文不足之處為在研究過程中未考慮不同駕駛員的駕駛特性以及換道工況等,且僅采用了聯合仿真進行驗證,后續還需進一步研究與進行硬件在環驗證。3 ACC分層控制設計
3.1 上層控制器設計
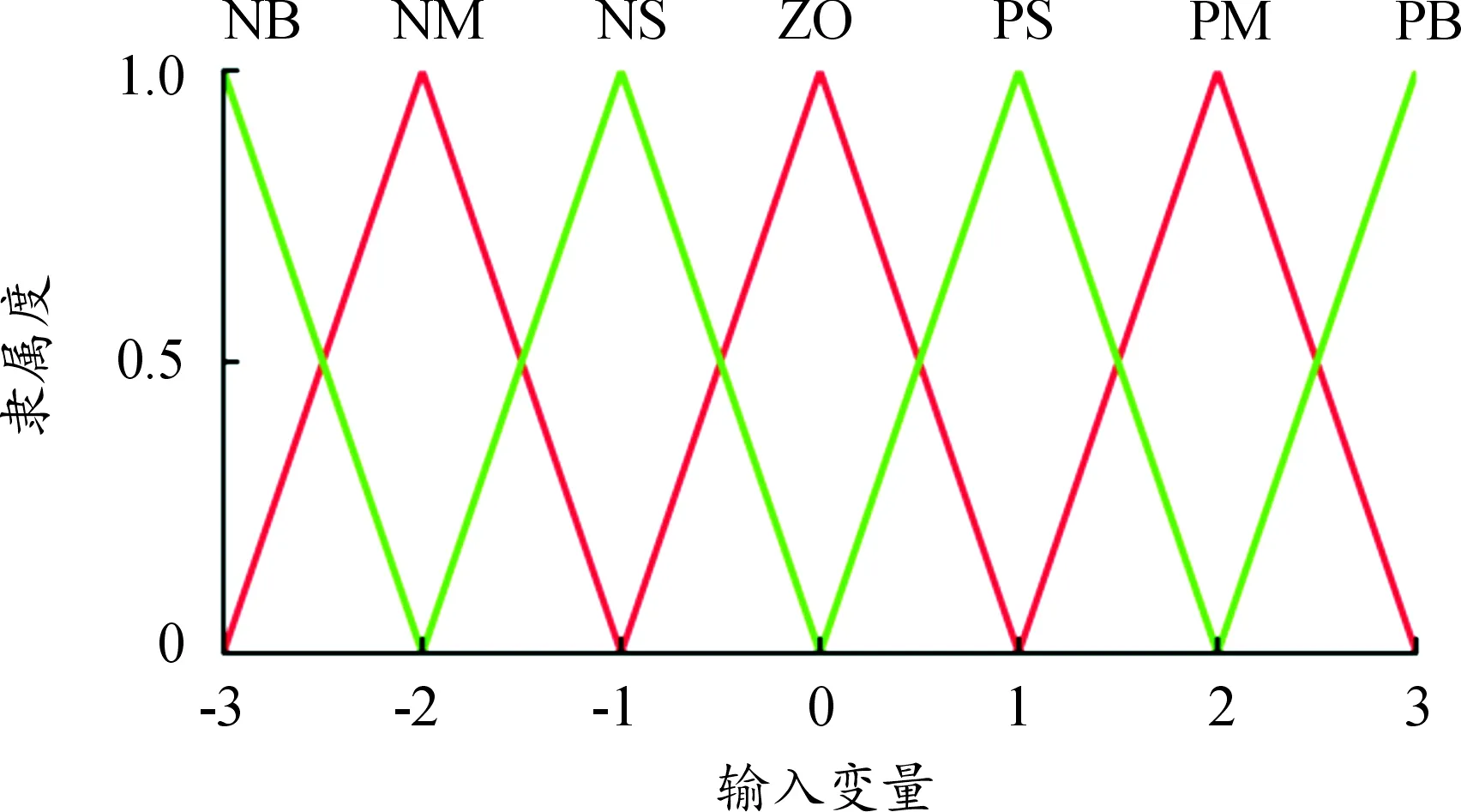
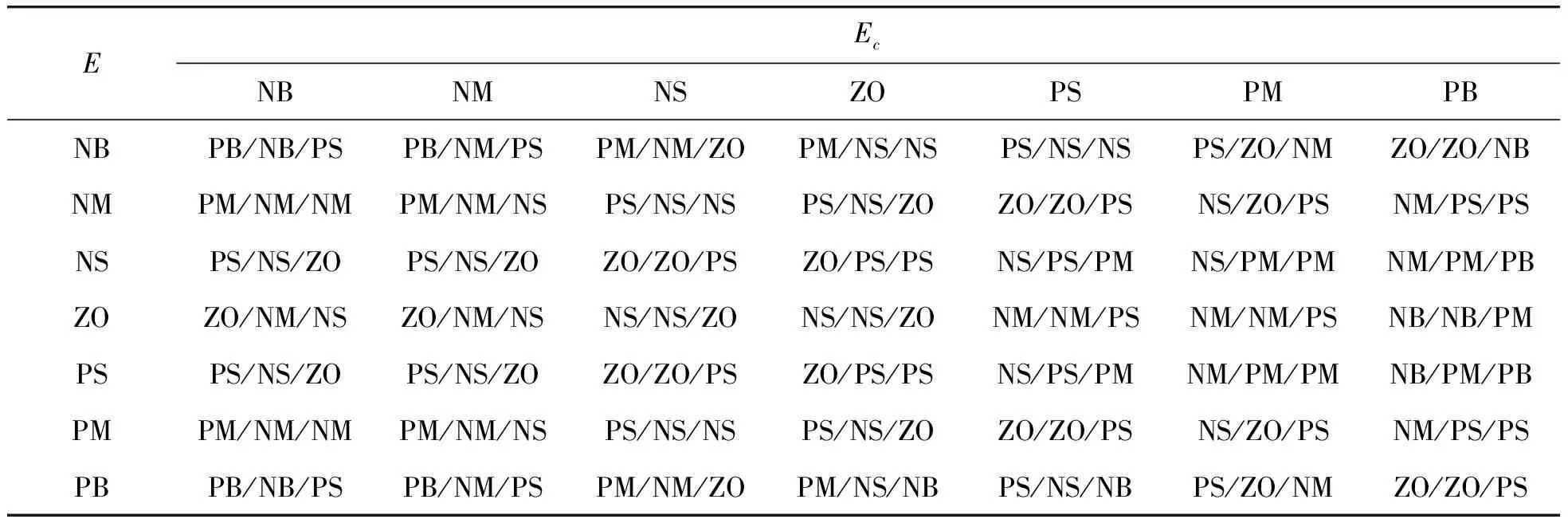

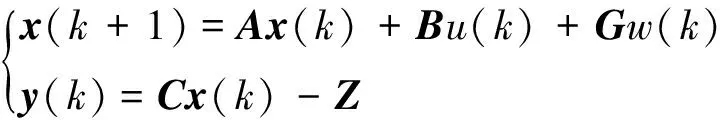

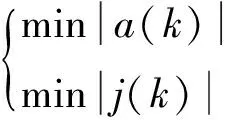

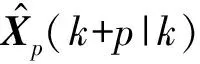
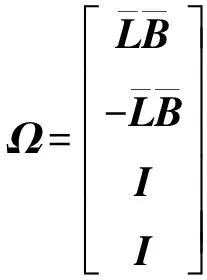
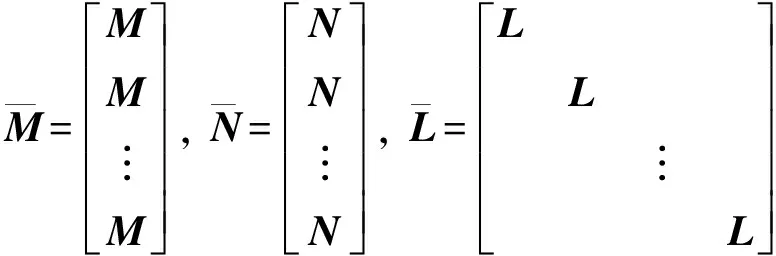
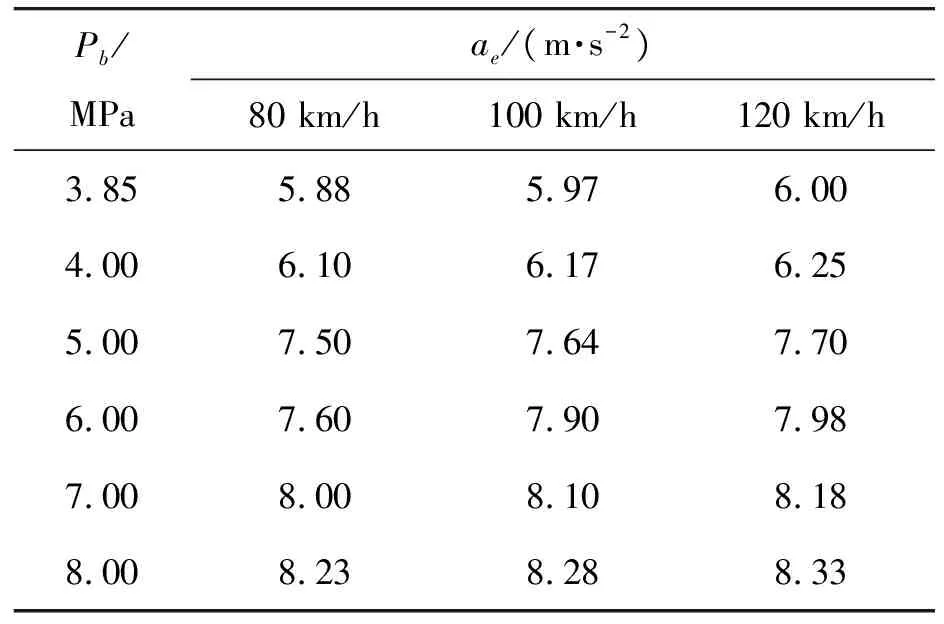
3.2 下層控制器設計
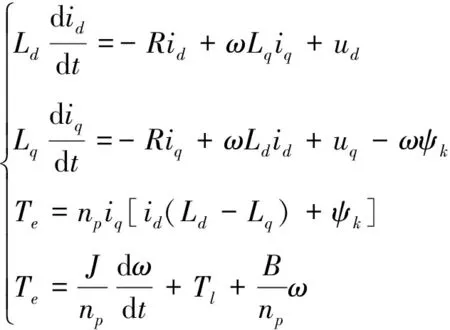
4 聯合仿真驗證與分析

4.1 仿真工況設置與結果分析
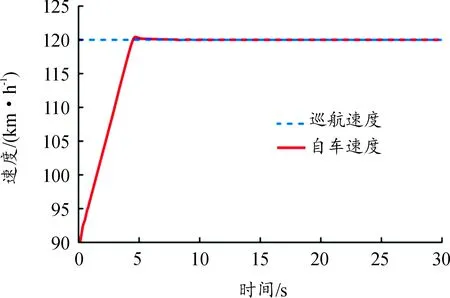






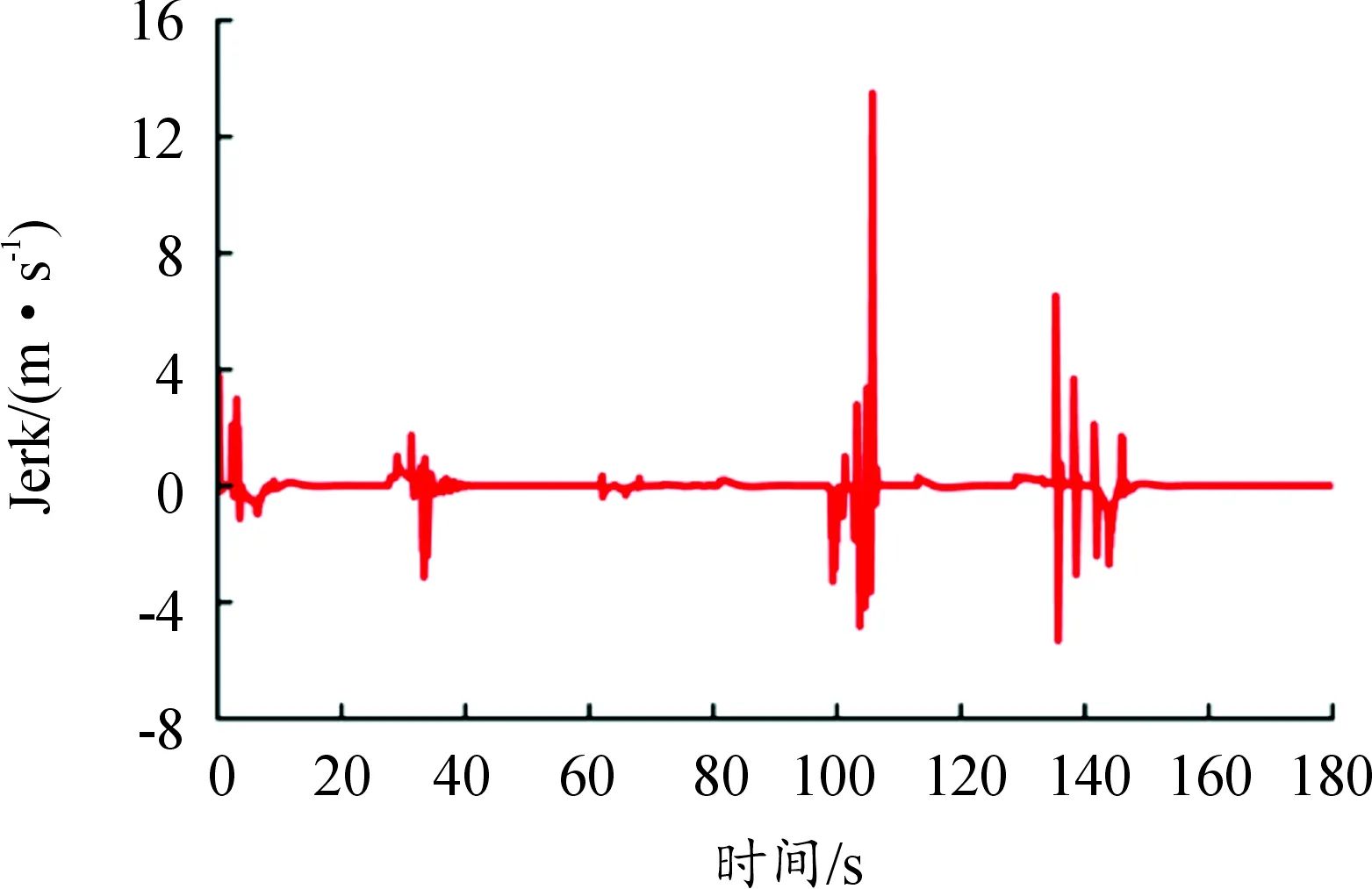
5 結論

