高速直齒輪齒面有限元網格精準離散方法

黃一倫,陳 旭,胡玉梅

(1.重慶理工大學 車輛工程學院, 重慶 400054;2.重慶大學 機械傳動國家重點實驗室, 重慶 400044)

有限元作為一種常用的齒輪嚙合仿真分析方法,被廣泛應用于齒輪動力學性能的研究,其中齒輪齒面在進行有限元網格離散時,網格的大小對于齒輪嚙合有限元仿真結果的正確性影響很大。在過去幾十年間,國內外許多學者針對齒輪有限元網格離散的問題展開了研究。劉更等[1-2]通過程序編寫出不同的齒廓網格節點生成函數,根據計算得到的節點坐標自動生成輪齒有限元網格。穆慧勇等[3]將斜齒輪齒根中點拉應力值取得平衡時的初始網格密度作為齒面齒向網格密度。張濤等[4]通過ANSYS的參數化程序語言,利用8節點六面體單元對齒輪進行有限元離散。曹雪梅等[5]利用刨齒展成法精確計算出齒面節點坐標,在旋轉投影平面上劃分網格,最終映射到齒面上。李紅勛等[6]綜合計算時長、精度和收斂性等因素,將齒面網格細化,而輪轂基體網格設置較稀疏。Coy等[7]提出了一種考慮赫茲變形影響的齒面網格尺寸選擇方法。Vijayakar等[8]通過結合曲面積分法和傳統有限元分析方法研究了齒輪齒面的有限元網格離散問題。Gonzalez-Perez等[9-11]研究了考慮齒輪扭轉變形和軸偏轉影響時的有限元網格劃分方法。Gonzalez-Perez等[12]提出了一種基于多點約束的齒輪傳動有限元模型網格細化策略。

綜上所述,國內外學者對齒輪有限元網格離散研究已經取得了豐碩成果,然而這些研究并未考慮齒面有限元網格尺寸在高轉速下的適應性問題。隨著現代航空航天技術的不斷發展,高線速直齒圓柱齒輪作為航空發動機動力傳輸的關鍵零部件具有質量輕、轉速高和載荷大等特性,其服役過程呈現強烈的非線性和瞬態性,所以對該類齒輪齒面有限元網格離散化的精度提出了更高要求。為此,本課題組用兩圓柱滾子曲面接觸有限元模型來模擬齒面接觸,通過有限元仿真分析不同轉速下兩圓柱滾子接觸產生的滑移能損失,提出一種齒面網格大小能夠適應齒面滾滑速度以及曲率半徑變化的齒面有限元網格精準離散方法。

1 齒面嚙合簡化模型

在齒輪嚙合過程中,輪齒之間的接觸屬于2個曲面之間接觸,而曲面有限元離散的基本思想是用有限個單元去近似模擬連續光滑的曲面體,要達到同等的離散化精度,曲率半徑越小的曲面,所需要的單元網格尺寸也越小。此外,高線速直齒輪轉速較高,齒面有限元網格存在較大的離心力,導致齒面有限元模型在參與嚙合時會產生單元網格之間的沖擊振動,這與實際的齒面接觸存在一定誤差。所以要想建立精確的齒面接觸有限元模型,關鍵問題是找到在不同轉速下齒面有限元網格尺寸與齒面曲率半徑之間的最佳倍數關系。

滑移能損失是2個相對滑動的面碰撞所導致的能量交換,不可避免。曲面接觸的滑移能損失與摩擦系數及正壓力有關,理論滑移能損失E可以表示為:

E=f×F×Vt×t

(1)

式中:f為接觸摩擦系數;F為垂直載荷,N;Vt為兩接觸面的相對滑動速度,m/s;t為時間,s。齒輪嚙合過程中的能量損失主要來源于輪齒之間的滑移能損失,所以輪齒之間的滑移能損失在一定程度上能夠反映出輪齒之間的接觸狀態。由于齒面上不同嚙合位置處的齒面壓力以及相對滑移速度均不相同,所以理論求解齒面滑移能損失存在一定難度。直齒輪的漸開線齒廓本質上是由一系列曲率半徑不同的圓弧所組成的光滑曲線,并且齒面接觸區寬度遠遠小于接觸區域的曲率半徑,因而可以對嚙合齒面作適當簡化。根據Weck等[13]試驗結果表明,在相同工作條件下,嚙合輪齒之間的接觸狀態可以簡化為2個圓柱滾子沿其母線方向上的接觸,如圖1所示。圖1中圓柱體滾子的半徑R1、R2分別代表齒輪嚙合位置處的齒面曲率半徑;n1和n2為圓柱滾子的轉速,上下圓柱滾子接觸點處的線速度分別代表主從輪齒齒面在嚙合位置處的切向速度;圓柱滾子垂直向下的壓力F代表齒面嚙合位置處的法向載荷;b代表齒寬。

圖1 圓柱滾子曲面接觸模型簡圖

2 直齒輪嚙合幾何分析

圓柱滾子曲面接觸模型能精準模擬高線速直齒圓柱齒輪齒面嚙合的前提是對其施加準確的邊界條件以及設置合理的幾何參數,其中包括圓柱滾子的曲率半徑、轉速以及垂直載荷,而這些邊界條件和幾何參數的值與高線速直齒圓柱齒輪的齒面曲率半徑、齒面切向速度、相對滑移速度以及齒面法向載荷的大小密切相關。本課題組根據直齒圓柱齒輪漸開線齒廓的嚙合過程,通過理論推導得出這些參數的計算方法。

圖2為直齒輪齒廓嚙合過程示意圖。P為節點,K1點和K2點是嚙合線上任意位置嚙合點。N1N2為理論嚙合線,B1B2為實際嚙合線,主動輪從B1點進入嚙合并推動從動輪的齒頂旋轉,從動輪在B2點與主動輪齒頂脫離嚙合。

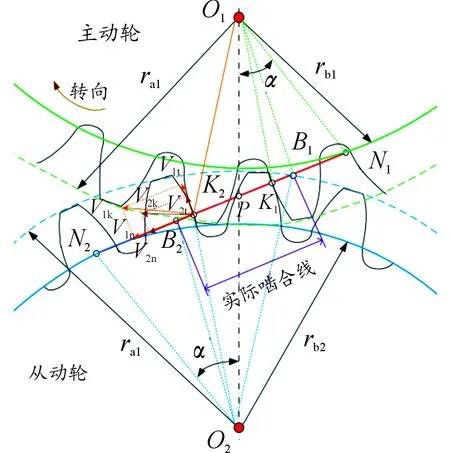
圖2 齒輪齒廓嚙合過程簡圖

根據齒廓嚙合過程中的幾何關系可知,齒面上任意嚙合點的曲率半徑等于齒面漸開線的發生線長度,即圖2中嚙合點距離N1點或N2點的長度,所以任意嚙合點在主、從動輪上的曲率半徑可以表示為:

(2)

(3)

式中:ρ1為任意嚙合點在主動輪上的曲率半徑;ρ2為任意嚙合點在從動輪上的曲率半徑;α為分度圓壓力角;r1為主動輪分度圓半徑;r2為從動輪分度圓半徑;rk為任意嚙合點在主動輪上的半徑;rb1為主動輪基圓半徑。

圖2中的V1k、V1t、V1n分別是嚙合點K2在主動輪上的絕對速度、切向速度以及法向速度,根據任意嚙合點K2在主動輪上的速度矢量三角形與直角三角形⊿K2O1N1的相似關系,主動輪上任意嚙合點沿齒面的切向速度V1t可以表示為:

(4)

式中:n1為主動輪轉速,r/min;ρ1為任意嚙合點K2在主動輪上的曲率半徑,mm;V1t為主動輪上任意嚙合點K2沿齒面的切向速度,m/s。

圖2中的V2k、V2t、V2n分別是嚙合點K2在從動輪上的絕對速度、切向速度以及法向速度,根據任意嚙合點K2在從動輪上的速度矢量三角形與直角三角形⊿K2O2N2的相似關系,從動輪上任意嚙合點沿齒面的切向速度V2t可以表示為:

(5)

式中:n2為從動輪轉速,r/min;ρ2為任意嚙合點K2在從動輪上的曲率半徑,mm;V2t為從動輪上任意嚙合點K2沿齒面的切向速度,m/s。

主、從動輪任意嚙合點處的相對滑移速度Vt可以表示為:

Vt=V1t-V2t

(6)

利用式(2)(3)計算出主從動輪齒面的最大最小曲率半徑大小,并將其作為圓柱滾子曲率半徑的確定依據。利用式(4)—(6)計算出最大齒面切向速度和相對滑移速度作為圓柱滾子模型中滾子轉速的確定依據。

此外,圓柱滾子的垂直載荷大小應當與航空高速重載直齒圓柱齒輪的齒面法向載荷相對應。直齒圓柱齒輪齒輪從動輪齒受力分析如圖3所示,其中d2為從動輪分度圓直徑,T為扭矩。為了計算圖3中的齒面名義法向載荷Fn,將其在分度圓處分解為圓周力Ft和徑向力Fr,根據力平衡條件和各力之間的幾何關系,齒面名義法向載荷Fn可以表示為[14]:

(7)

式中:rb2為從動輪基圓半徑;P為從動輪輸出功率,kW。

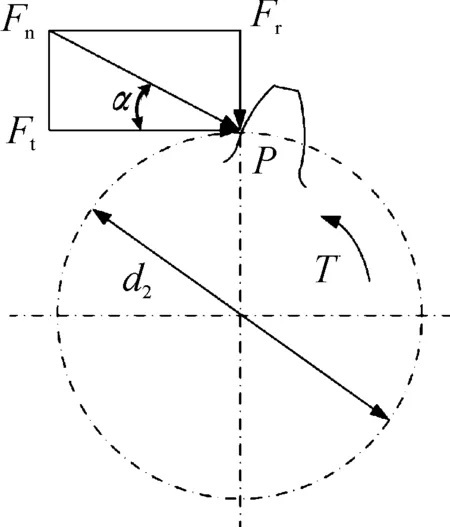
圖3 直齒圓柱齒輪輪齒受力分析

根據式(7)可以求出齒面法向載荷的大小,并將其作為圓柱滾子模型中滾子垂直載荷的確定依據。

3 建模與仿真分析

以某在研航空發動機齒輪箱為研究對象,根據式(2)—(7)分別計算得出齒輪箱中所有直齒圓柱齒輪的齒面曲率半徑、齒面切向速度、齒面相對滑移速度以及齒面載荷,并最終總結得出的航空發動機高速重載齒輪齒面曲率半徑、齒面切向速度、齒面相對滑移速度以及齒面載荷的大致范圍如表1所示。基于此范圍確定圓柱滾子的曲率、轉速以及載荷等參數大小。

由于相對滑移速度的大小隨著兩接觸面的切向速度變化而變化,所以為了定量分析齒面切向速度對主從輪齒接觸的影響,保持圓柱滾子接觸面之間的相對滑移速度Vt為20 m/s。直齒圓柱齒輪理想潤滑條件下的齒面摩擦系數為0.01～0.02[15],所以滾子之間的接觸摩擦系數固定為0.01。

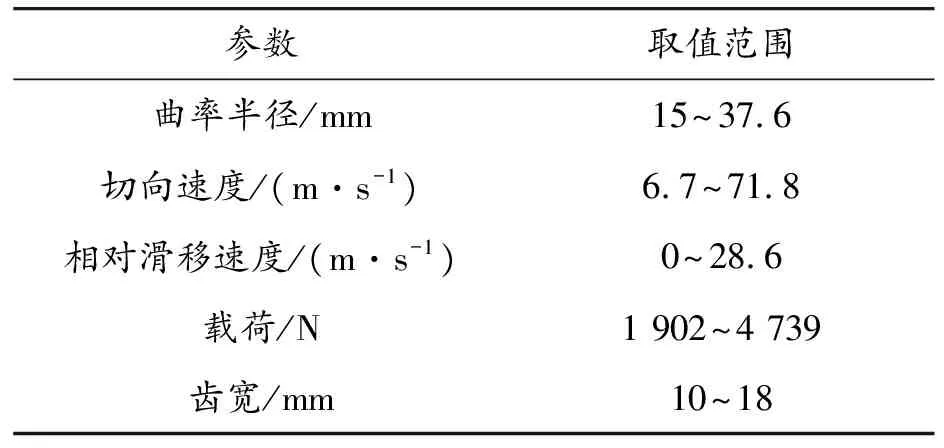
表1 航空發動機高速重載齒輪齒面曲率、速度和載荷等參數范圍

分別建立4組接觸面切向速度不同的圓柱滾子曲面接觸模型,具體參數如表2所示。

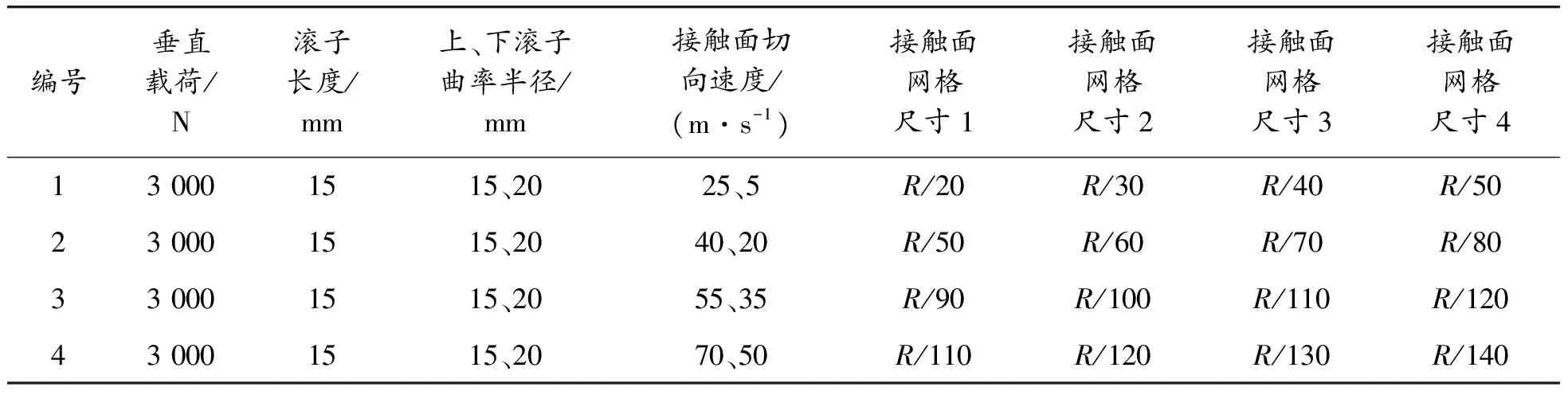
表2 圓柱滾子曲面接觸模型參數

圖4為圓柱滾子曲面接觸有限元模型。分別對上下滾子施加大小不同的轉速,并在上滾子軸心線的節點上施加豎直向下的均布載荷,最后在上下滾子的接觸面之間建立接觸。

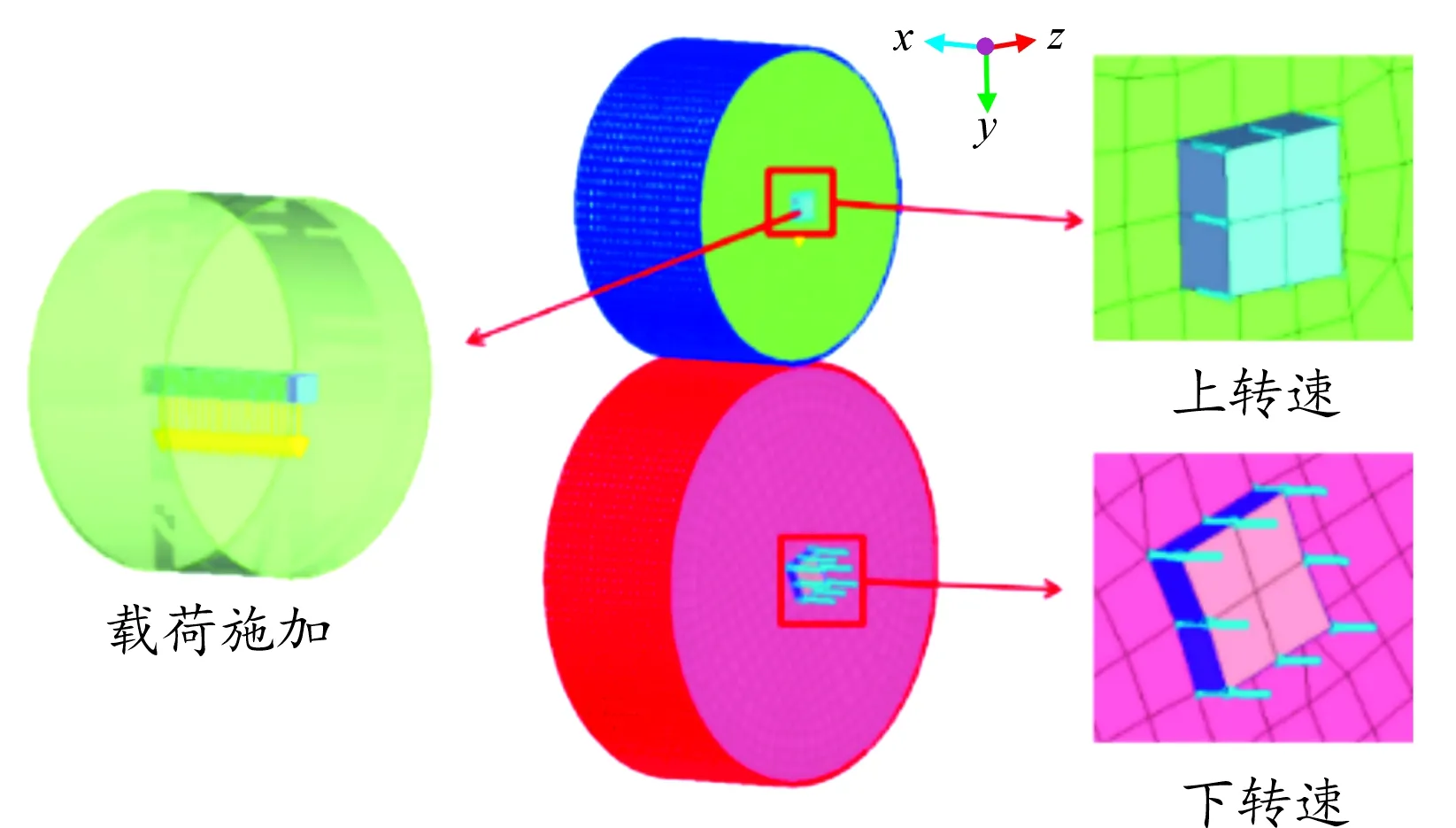
圖4 圓柱滾子曲面接觸有限元模型

將模型導入ANSYS軟件中使用LS-DYNA求解器仿真計算。對于線速度大于20 m/s的航空發動機直齒圓柱齒輪,單對輪齒的嚙合時間往往不超過0.001 s,所以將兩圓柱滾子在0.001 s時間內接觸產生的滑移能仿真值與理論值之間的百分比誤差小于10%作為前提,對比分析得出在不同切向速度下曲面網格尺寸大小與曲率半徑之間的最佳倍數關系。

圖5分別為表2中4組圓柱滾子曲面接觸模型在0.000 2、0.000 4、0.000 6、0.000 8、0.001 s時的滑移能損失誤差曲線。

圖5 不同切向速度下的圓柱滾子滑移能誤差曲線

根據以上仿真結果可知,隨著網格的細化,滑移能誤差百分比值呈現逐漸減小的趨勢,而隨著時間的推移,滑移能仿真值與理論值之間百分比誤差維持在小范圍內波動,基本保持恒定。同時,在相同的網格細化程度下,滑移能誤差百分比與2個滾子接觸曲面之間最大切向速度的絕對值成正比關系,最大切向速度越大,則滑移能誤差百分比值越大。對于最大切向速度為25 m/s的滾子模型,接觸面網格尺寸為R/40～R/50時的滑移能百分比誤差相對較小,滿足建模精度要求。最大切向速度為40 m/s時,接觸面網格尺寸為R/70～R/80時的滑移能百分比誤差小于10%。最大切向速度為55 m/s時,接觸面網格的細化程度最少要達到R/110才能達到建模精度要求。而當最大切向速度為70 m/s的滾子模型,接觸面網格的細化程度至少需要要達到R/140,才滿足誤差小于10%的工程精度要求。綜合誤差、齒輪齒面參數以及模型計算時間等多方面因素,總結出滿足工程建模精度的高速齒輪齒面網格細化準則,如表3所示。

表3 直齒圓柱齒輪齒面網格尺寸確定標準

4 算例與驗證

為了證明上述方法的有效性,以某在研航空發動機齒輪箱中的一對直齒圓柱齒輪副為例,根據表3中給出的齒面網格離散準則劃分齒輪齒面有限元網格,并分別建立4組不同轉速工況下的齒輪嚙合有限元模型,對其進行仿真分析。齒輪基本參數如表4所示。

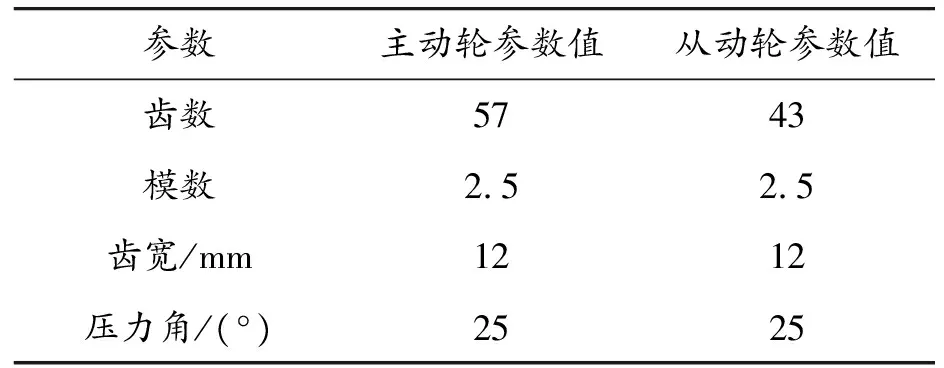
表4 航空發動機齒輪箱中某直齒圓柱齒輪副參數

利用式(2)(3)可以計算出主從輪齒齒面的最小曲率半徑分別為24.7 mm和17.2 mm,利用式(4)—(6)計算出4種轉速下齒輪副輪齒嚙入到嚙出過程中的最大齒面切向速度,并根據表3確定出該齒輪副在4種轉速下的最佳齒面有限元網格尺寸,如表5所示。

以表5中的第一組工況為例,說明齒輪副嚙合有限元模型的建模方法(其余工況除轉速、扭矩及齒面網格尺寸不同外,建模流程均相同)。圖6為主從輪齒齒面有限元模型。其中齒面體網格均使用六面體網格,齒廓線上的節點間距以及齒向方向的網格節點間距均等于表5中計算得出的齒面網格尺寸。

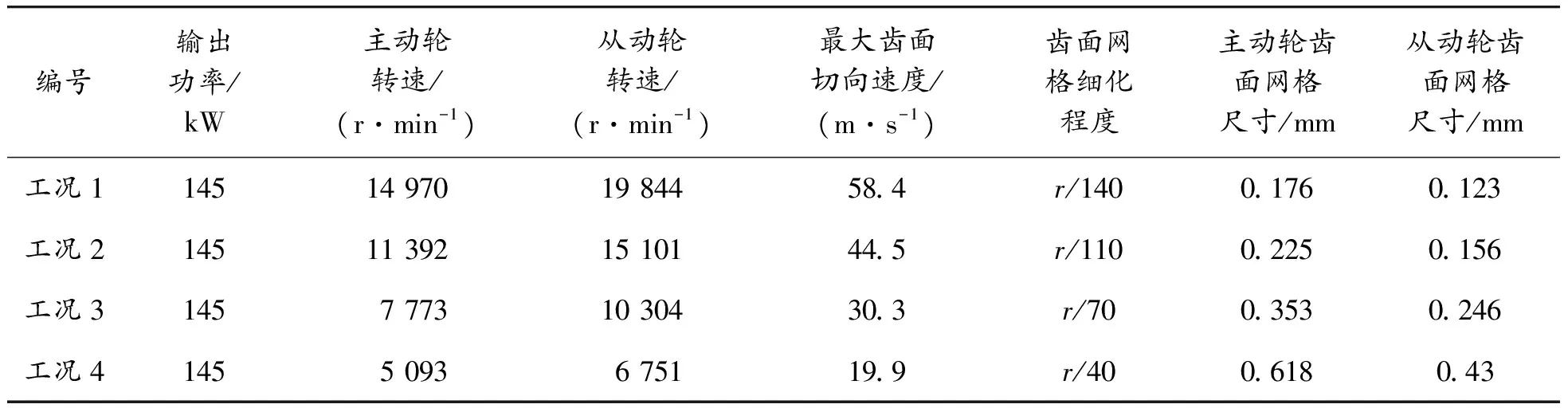
表5 不同工況下的最佳齒面有限元網格尺寸

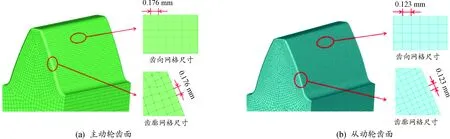
圖6 主從輪齒齒面有限元模型

如圖7所示,分別以對主從動輪施加轉速、轉矩及接觸為邊界條件,建立齒輪副嚙合有限元模型。最終導入ANSYS中利用LS-DYNA求解器進行仿真求解。

分別提取齒輪接觸力穩定階段時4種不同轉速下節點位置處的齒面接觸應力,如圖8所示。根據仿真結果可知,主從輪齒齒面接觸區的應力呈較為理想的橢圓形分布,表5中工況1、工況2、工況3和工況4所對應的最大齒面接觸應力分別為608.6、545.2、597.2和666.5 MPa。

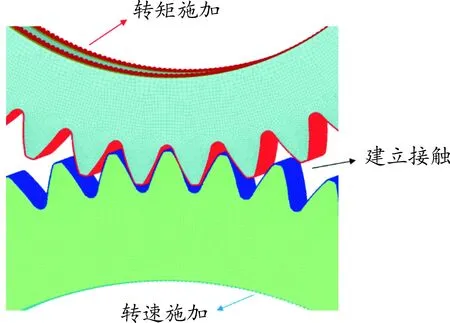
圖7 齒輪副嚙合有限元模型

圖8 4種工況下的齒面接觸壓應力

參考國家標準[16],齒輪使用系數、齒間載荷分配系數及齒向載荷分布系數均取1,而表5中的工況1、工況2、工況3和工況4所對應的動載系數分別取1.65、1.44、1.21和1.06,根據赫茲公式計算得出的最大齒面接觸應力理論值分別為557.8、597.3、662.9和706.5 MPa,與仿真值之間的誤差分別為9.1%、8.7%、9.9%和5.6%。說明上述高速直齒圓柱齒輪齒面有限元網格離散方法能保證不同轉速下的齒輪有限元仿真誤差小于10%。

同理,相比于表5中的齒面網格尺寸,在工況1的條件下,分別采用一組更大(主從動輪齒面網格尺寸為0.35 mm)和一組更小(主從動輪齒面網格尺寸分別為0.095 mm)的網格尺寸對齒面進行離散,并采用相同的建模方法建立齒輪嚙合有限元模型,并對其仿真分析。分別提取2種不同齒面網格尺寸下節點位置處的齒面接觸壓應力,如圖9所示。根據仿真結果可知,大網格條件下所對應的最大齒面接觸應力為340.5 MPa,與理論值之間的誤差為39%,仿真精度明顯變差;而小網格條件下所對應的最大齒面接觸應力為541.3 MPa,與理論值之間的誤差為3%,仿真精度有所提高。如圖10所示,對比3種網格尺寸下的仿真誤差及仿真時間可知,齒面網格尺寸越小,有限元仿真精度越高,但同時仿真時間也會大幅延長。說明采用表3所推薦的齒面網格尺寸,既保證了齒輪有限元仿真的精度,也將仿真時長控制在了可接受范圍之內,證明上述高線速直齒圓柱齒輪齒面有限元網格離散方法是正確有效的。

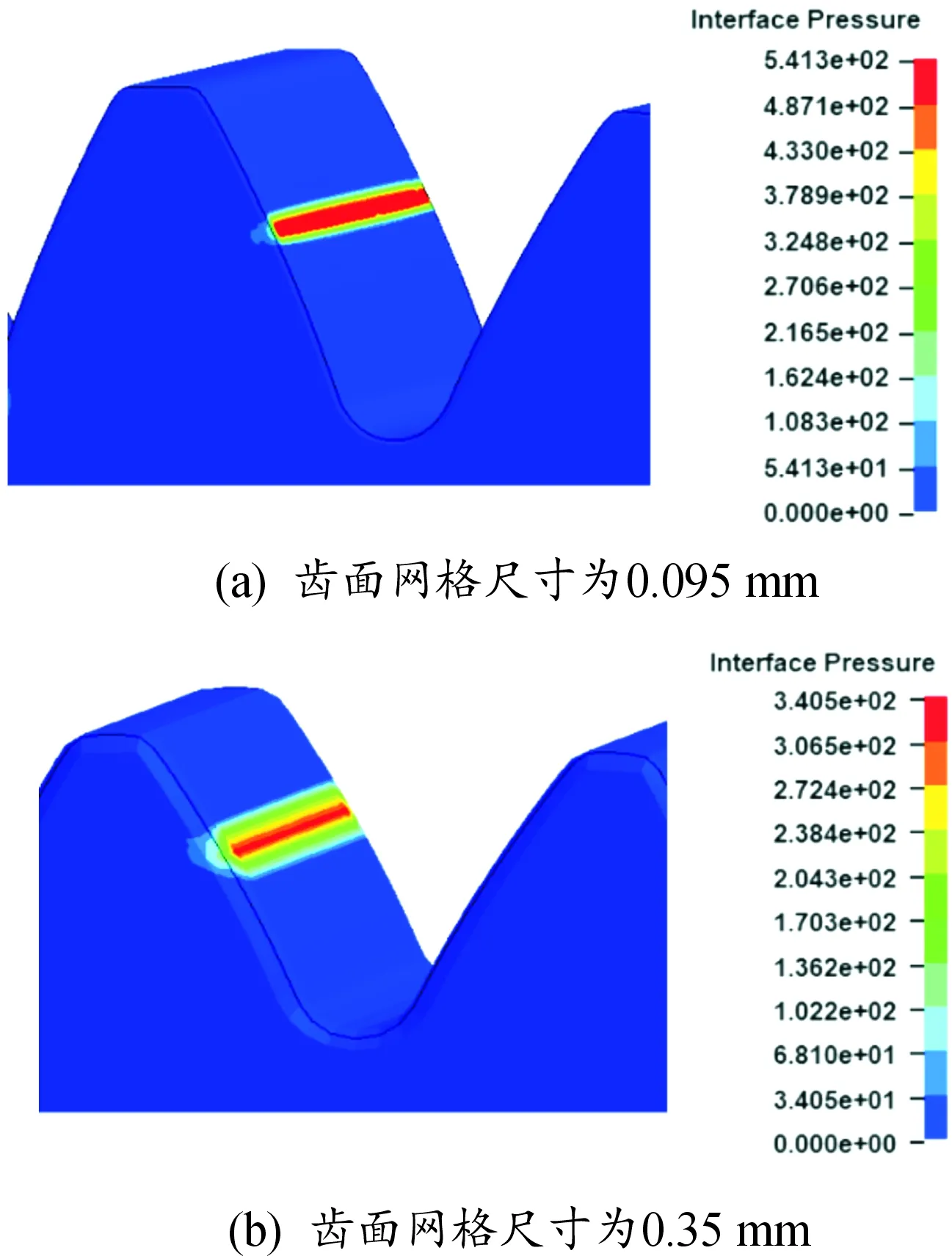
圖9 不同齒面網格尺寸下的齒面接觸壓應力

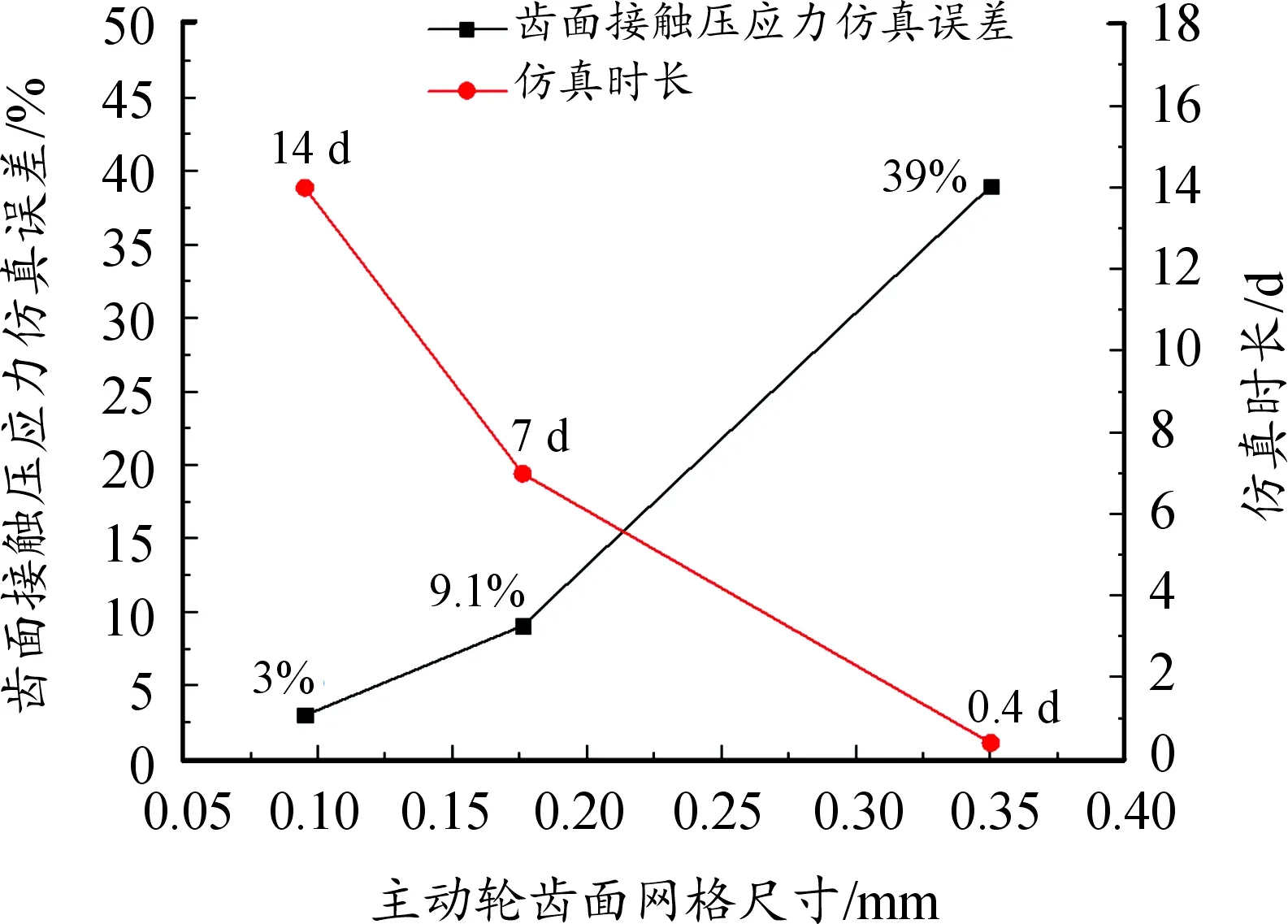
圖10 不同齒面網格尺寸下的齒面壓應力誤差及仿真時長

5 結論

1) 當最大齒面切向速度在0～25 m/s時,齒面網格尺寸應當取齒面最小曲率半徑的1/40。

2) 當最大齒面切向速度在25～40 m/s時,齒面網格尺寸應當取齒面最小曲率半徑的1/70。

3) 當最大齒面切向速度在40～55 m/s時,齒面網格尺寸應當取齒面最小曲率半徑的1/110。

4) 當最大齒面切向速度在55～70 m/s時,齒面網格尺寸應當取齒面最小曲率半徑的1/140。

5) 采用上述齒面有限元網格離散方法所得到的有限元模型,其仿真結果與理論值誤差小于10%。