基于AOA-LSTM的施工升降機電機軸承剩余壽命預測
郗 濤,王 通,王莉靜,張建業
(1.天津工業大學 機械工程學院,天津 300387; 2.天津城建大學 控制與機械工程學院,天津 300384)
施工升降機是建筑領域廣泛應用的工程機械,其中,電機主軸軸承作為施工升降機的關鍵零部件,一旦失效將會導致升降機及整個建筑作業的停工。失效的主要由軸承的故障及運行過程中的壽命退化引起,為在軸承達到失效點前判斷其健康狀況,對軸承進行退化狀態評估和剩余壽命預測具有重要作用[1-3]。
近年來,滾動軸承的剩余壽命預測是機械設備預測和健康管理領域的熱點研究話題之一,目前研究領域主要基于數據驅動的方法建立預測模型[4]。徐洲常等[5]通過主成分分析(principal component analysis,PCA)方法把提取的高維退化特征融合成歸一化指標,并輸入到回歸型支持向量機(support vector machine,SVM)預測模型中進行軸承的壽命預測;胡小曼等[6]利用相關向量機(relevance vector machine,RVM)建立預測模型進行滾動軸承剩余壽命預測,取得較好的預測結果。隨著深度學習的發展,神經網絡預測模型被廣泛應用于軸承壽命預測。王奉濤等[7]提出長短時記憶網絡的壽命預測方法;尹詩等[8]利用雙向循環神經網絡(bidirectional recurrent neural network,BI-RNN)的方法預測風電機組主軸承的剩余壽命;韓林潔等[9]提出雙向長短時記憶網絡(bi-directional long short term memory,BILSTM)的滾動軸承剩余壽命預測方法。上述研究雖然在設備壽命預測方面取得了較好的成果,但在工程機械領域的應用較少,同時預測模型的關鍵參數由經驗值確定,準確率較低。
因此,本文提出一種基于算術優化算法和長短時記憶網絡(arithmetic optimization algorithm and long short term memory,AOA-LSTM)的施工升降機電機軸承剩余壽命預測方法。首先,對原始振動信號提取時域和頻域特征指標;其次,利用隨機森林算法,對提取的高維特征指標進行重要度分析,選擇重要度高的特征指標構建退化特征決策表;最后,利用算術優化算法(arithmetic optimization algorithm, AOA)長短時記憶網絡(long short term memory,LSTM)模型中的網絡層數、每層網絡神經元個數和學習率,選擇最優參數建立預測模型,并采用均方根誤差(root mean square,RMSE)和平均絕對誤差(mean absolute error,MAE)指標評估預測模型。該方法分別利用西安交通大學(Xi’an Jiaotong University and the Changxing Sumyoung Technology,XJTU-SY)驗證數據集和某施工升降機電機軸承的采集數據,并取得較好的預測結果,證明該方法的可行性和魯棒性。
1 理論基礎
1.1 算術優化算法
AOA 是Abualigah 等[10]在2021 提出的元啟發式新型智能優化算法,具有良好的收斂速度和求解精度,核心原理是利用基本的算術運算實現算法的尋優過程,其中乘除運算更新全局最優位置,避免產生局部解;加減運算更新局部最優位置,提高求解精度。算術優化算法優化過程分初始化階段、探索階段和開發階段3 個階段。其中,探索階段包括除法運算(D)與乘法運算(M),開發階段包括加法運算(A)和減法運算(S)。
1.1.1 初始化階段
初始化參數,在參數范圍內隨機設置初始解X,每次迭代的最佳候選解確定為當前最優解,X為
式中:X為N×n維矩陣
在算法迭代開始前通過數學優化器加速函數(MOA)對探索階段或者開發階段進行選擇,取隨機數r1∈[0,1]與MOA 進行比較,r1≥fMOA選擇探索階段迭代尋優,反之選擇開發階段,MOA定義式為
式中:fMOA(t)為第t次迭代的函數值;t為當前迭代次數;Mt為最大迭代次數;fmax為fMOA的最大函數值;fmin為fMOA的最小函數值。
1.1.2 探索階段
在探索階段主要利用除法機制和乘法機制兩個搜索機制作為搜索策略,隨機數r2∈[0,1]與0.5進行對比,若r2>0.5 選擇最外層除法策略,反之選擇乘法策略。式(3)為位置更新函數,式(4)為探索階段迭代過程:
式中:fMOP(t)為t次迭代時的函數值;a為敏感參數。
式中:xi(t+1)為下一次迭代的第i個解;xi,j(t+1)為第i個解在當前迭代的第j個位置;fbest(xj)為當前迭代最優解的第j個位置;UBj和LBj為第j個位置的上界和下界;ε為一整數;m為調節搜索過程的控制參數。
1.1.3 開發階段
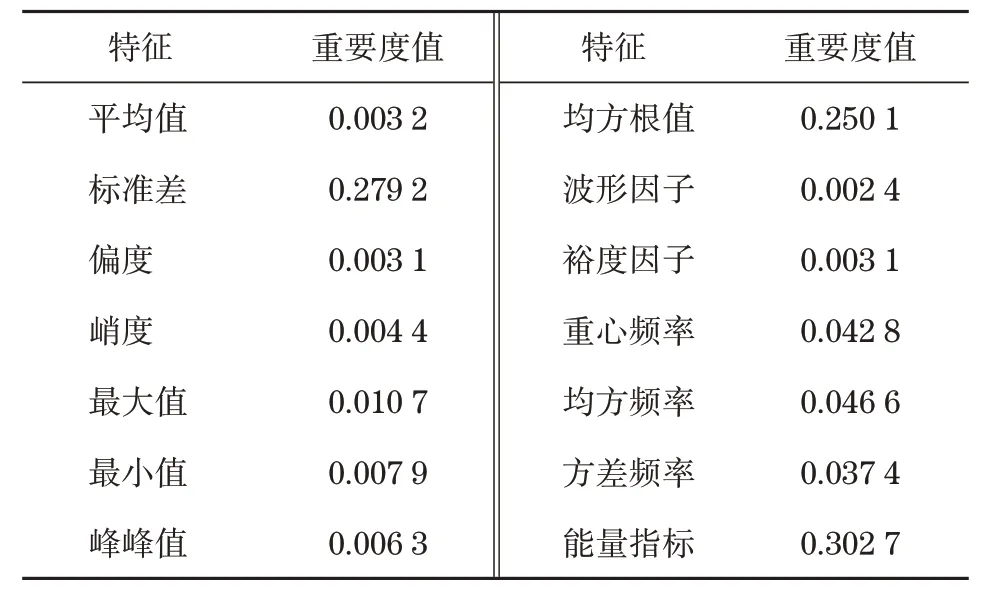
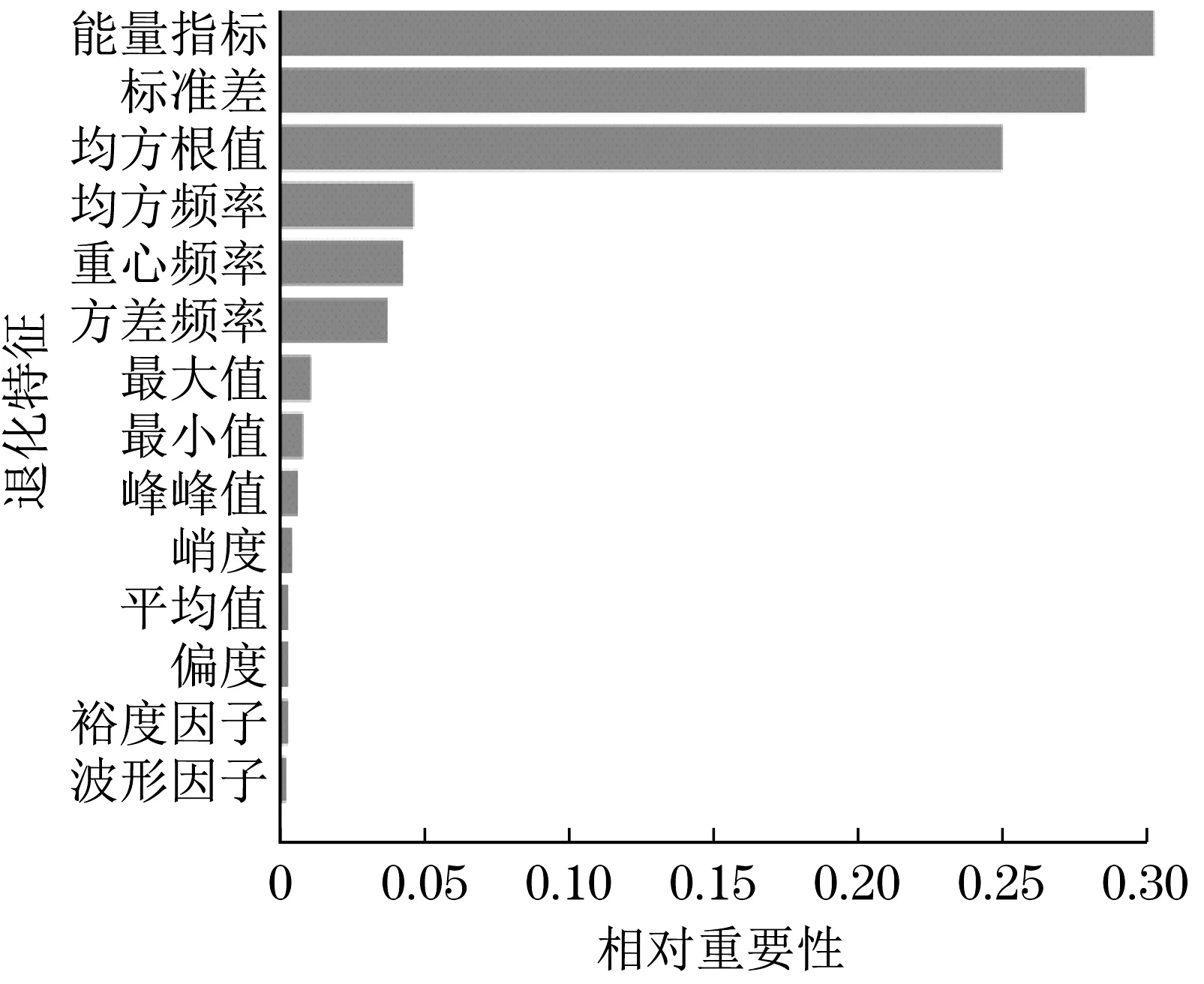
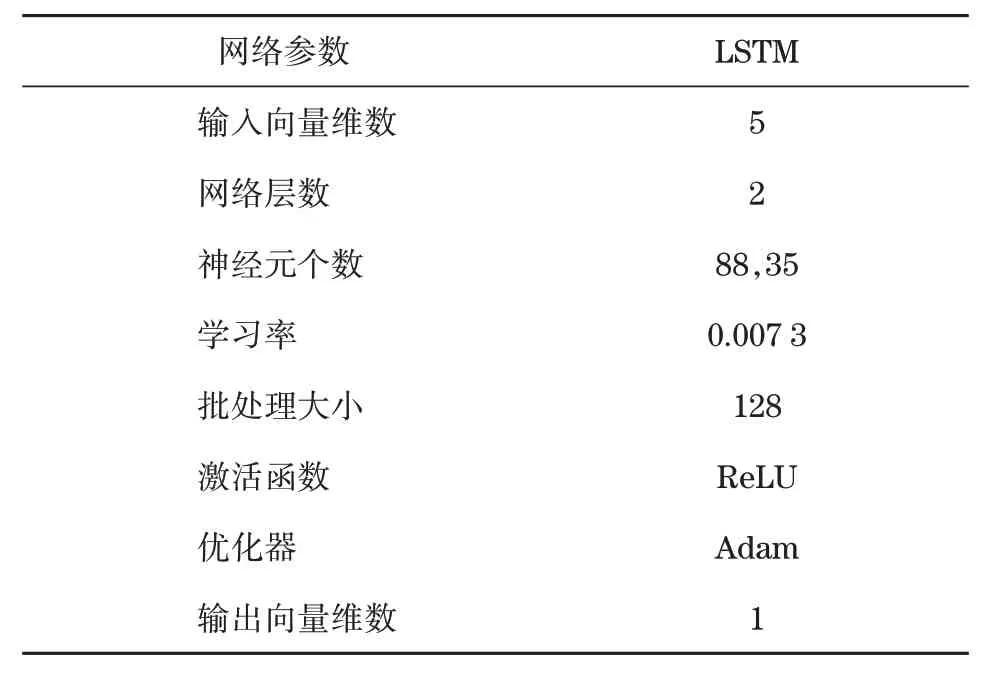
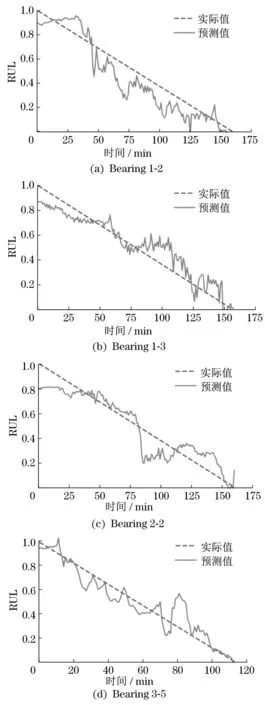
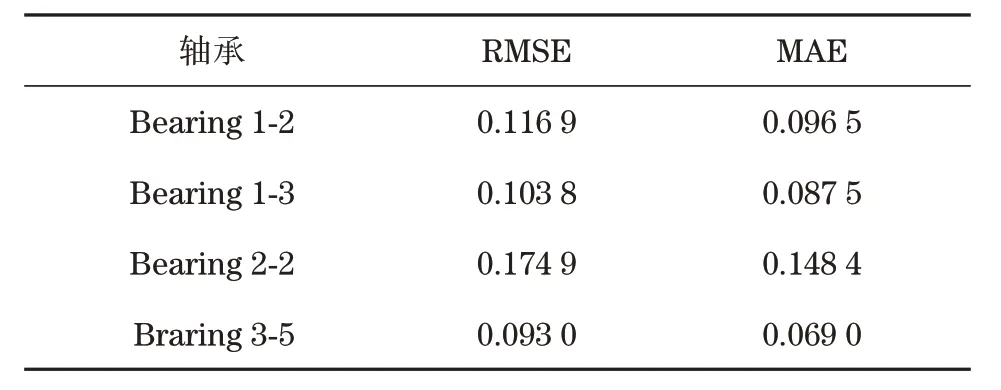
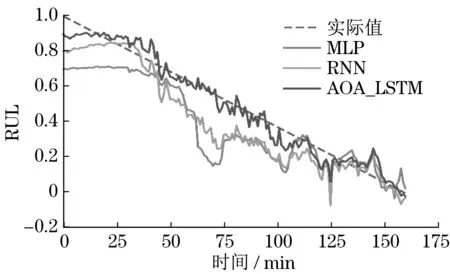
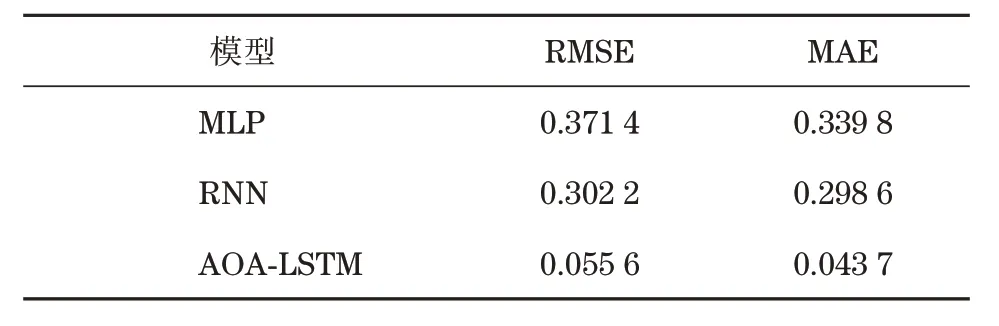
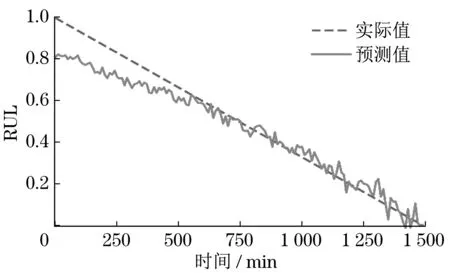
開發階段利用加法機制和減法機制作為搜索策略進行局部尋優,此階段搜索范圍小,準確度較高。當隨機數r1 式中:μ為調節搜索過程的控制參數。 循環神經網絡(recurrent neural network,RNN)適合處理時序數據,但在模型訓練過程中存在梯度消失、梯度爆炸等問題,LSTM[11]利用門控機制原理使模型具有更強的記憶能力,能夠處理更長的時序數據,同時解決了RNN 存在的梯度問題。LSTM 的3 個門控機制分別為遺忘門、輸入門和輸出門,門控機制通過激活函數把輸入數據壓縮到[0,1]區間內,同時控制數據的流動。 LSTM 模型結構如圖1 所示,箭頭方向為數據流動方向,ct-1、ct分別為上一個時間戳輸入的記憶數據和當前時間戳輸出的記憶數據,ht-1、ht分別為上一個時間戳的輸入數據和當前時間戳的輸出數據,xt為當前時間戳的輸入數據。 圖1 LSTM模型結構Fig.1 LSTM model structure 遺忘門為上一個時間戳的輸入ct-1和當前時間戳的遺忘門控制變量gf的乘積,輸出為gfct-1: 式中:Wf、bf為遺忘門的權重參數和偏置參數;xt為當前時間戳的輸入參數;ht-1為上一時間戳的輸出數據;σ為激活函數。 輸入門為輸入門控值變量gi和當前輸入數據經過tanh激活函數變換后的狀態向量乘積,輸出數據為?: 式中:Wc為輸入門的權重參數;bc為偏置參數;tanh為激活函數。 式中:Wi為輸入門的權重參數;bi為偏置參數。 輸出門為輸出門控值變量go和當前時間戳的輸出狀態向量的乘積,輸出數據為ht: 式中:Wo為輸出門的權重參數;bo為偏置參數。 LSTM 模型訓練過程中參數的選擇對網絡訓練結果影響較大,大部分研究通過經驗選擇LSTM網絡參數,但存在較大誤差。本文通過AOA 算法優化LSTM 中的超參數,并利用優化結果建立LSTM 預測模型,關鍵參數有學習率、網絡層數和每層網絡的神經元個數。因此,利用AOA 對以上參數尋找全局最優值,并選擇RMSE 作為適應度函數: 式中:p為預測值;y為真實值;n為預測樣本點個數。 算法優化步驟為: (1) 初始化AOA 算法參數,設置最大迭代次數,隨機選擇優化參數等,設置均方根誤差為適應度函數。 (2) 初始化LSTM 算法參數,設置批處理量等參數,通過初始化優化參數進行模型預測,得到當前迭代適應度值。 (3) AOA 不斷迭代更新參數位置,記錄每次最優結果,返回步驟2。 (4) 通過步驟2 和3 不斷迭代計算最佳適應度值,與記錄值對比確定當前最優值是否為最優解,滿足迭代條件則終止迭代,輸出最優結果,否則返回步驟2 和3 繼續更新位置,直到滿足迭代條件終止。 AOA-LSTM 預測模型的構建主要分為3 個階段,即對原始振動信號提取特征并構建退化特征、AOA 優化LSTM 中的超參數、LSTM 預測模型的建立與評估。AOA-LSTM 預測模型流程如圖2所示。 圖2 AOA-LSTM預測模型流程Fig.2 AOA-LSTM prediction model flow chart 退化特征的構建需要對原始數據提取時域和頻域特征指標。時域退化特征提取平均值、標準差、偏度、峭度、最大值、最小值、峰峰值、均方根值、波形因子和裕度因子;頻域退化特征提取重心頻率、均方頻率、頻率方差、能量等14 維退化特征,特征提取詳細公式參考文獻[3]。提取的高維特征指標利用隨機森林算法進行特征重要度分析,選擇與軸承實際退化特征相關性更高的特征構建退化特征決策表,輸入LSTM 預測模型中進行預測與分析。 LSTM 預測模型構建中,退化特征決策表作為訓練集輸入數據,對應的壽命標簽作為訓練集標簽,為消除不同量綱的影響,對退化特征進行歸一化處理,剩余壽命標簽初始為1,隨著軸承退化過程的進行,剩余壽命最終為0。模型訓練結束后輸入測試集數據,通過RMSE和MAE評估模型。 平均絕對誤差為 式中:p為預測值;y為真實值;n為樣本點個數。 選擇XJTU-SY 數據集[12]驗證該方法的可行性,該數據集包括3種工況下共15組滾動軸承的全生命周期數據,軸承數據集長度和故障類型等信息見表1。實驗中選擇的軸承型號為LSD UER204滾動軸承,采樣頻率為25.6 kHz,采樣間隔為1 min,采樣時間為1.28 s,即每次采樣樣本點為32 768。實驗中軸承施加載荷方向為水平方向,水平方向的加速度振動信號包含更多的有效退化信息,選擇該方向的數據進行實驗分析。Bearing 1-1 的全壽命軸承數據的時域如圖3 所示,由圖3 中可知軸承的全生命周期退化過程。 表1 退化特征相對重要性量化結果Tab.1 Quantitative results of relative importance of degradation characteristics 選擇Bearing 1-1 提取時域、頻域共14 維特征指標,再通過隨機森林算法對提取的特征指標進行重要度分析[13],其結果如圖4 所示。退化特征重要性量化結果見表1。選擇重要度值大于0.04的特征指標共5 維特征構建退化特征決策表,作為LSTM模型的輸入數據。 圖4 退化特征相對重要性Fig.4 Relative importance of degradation characteristics AOA 對LSTM 中的網絡層數、每層網絡神經元個數、學習率作為超參數進行優化,選擇均方根值作為適應度函數,設置AOA 參數進行模型超參數優化,優化結果為網絡層數為2,第1 層神經元個數為88,第2層為35,學習率為0.007 3。 通過AOA 優化結果構建LSTM 預測模型,LSTM網絡模型參數見表2。 表2 LSTM網絡模型參數Tab.2 LSTM network model parameter 模型訓練過程中,MES 損失曲線變化過程如圖5 所示,設置迭代次數1 000 次。由圖5 可知,訓練損失曲線和驗證損失曲線隨著迭代次數的增加趨于穩定。 圖5 損失曲線變化過程Fig.5 The loss curve change process 以Bearing1-1 作為訓練集,選擇其余4 種軸承作為測試集,不同工況下軸承預測結果如圖6 所示,縱軸為剩余使用壽命(remaining useful life,RUL)。由圖6 可知,預測值在一定范圍內隨著實際值上下波動,預測結果較好。 圖6 AOA-LSTM預測結果Fig.6 AOA-LSTM prediction results 利用RMSE 和MAE 評估預測模型,評估結果見表3。 表3 預測模型評估結果Tab.3 Prediction model evaluation results 為驗證文中所提方法的有效性,選擇MLP、RNN 算法與AOA-LSTM 算法對比。3 種不同算法的預測結果對比如圖7 所示。由圖可知,本文所提方法與實際值預測結果擬合度更高。 圖7 不同預測模型預測結果對比Fig.7 Comparison of prediction results of different prediction models 利用RMSE 與MAE 對3 種不同預測模型進行誤差評估,結果見表4。由表可知,AOA-LSTM 預測模型誤差更小,證明本文所提方法的有效性。 表4 不同預測模型評估結果Tab.4 Evaluation results of different prediction models AOA-LSTM 模型在工程應用中,對某施工升降機的電機軸承采集振動信號數據,該數據包含電機軸承全壽命階段的共150 組退化數據,每組數據包含2 000 個樣本點,采樣間隔為10 min。利用本文所提研究方法對采集的振動信號提取特征指標,并提取退化特征后輸入AOA-LSTM 預測模型中,預測結果如圖8 所示。由圖8 可知,在軸承退化階段和失效階段,預測結果準確度更高,利用RMSE 和MAE 評估模型,計算結果分別為0.075 8和0.057 4,所提退化特征提取方法和預測模型具有較好的泛化性。 圖8 采集數據預測結果Fig.8 Collect data prediction results 本文提出一種基于AOA-LSTM 的施工升降機電機軸承剩余壽命預測方法,通過理論模型與工程實際應用相結合,預測結果較準確,得到以下結論。 (1) 對原始振動信號提取時域和頻域特征指標,并利用隨機森林算法進行重要度分析,進一步選擇的退化特征與實際退化過程相關性更高。 (2) 通過AOA 對LSTM 神經網絡尋找最優參數組合,避免經驗選擇參數的不足,對XJTU-SY 數據集中不同工況的滾動軸承進行預測,預測結果準確度較高。與MLP 和RNN 模型對比,所提方法的預測誤差更小。 (3) 分別通過XJTU-SY 數據集和某施工升降機電機軸承的采集數據驗證所提方法,XJTU-SY數據集上預測結果:RMSE、MAE 分別為5.56%和4.37%,采集數據RMSE、MAE 分別為7.58% 和5.74%,預測結果具有較高的準確率,證明所提方法的可行性。1.2 LSTM模型及參數優化
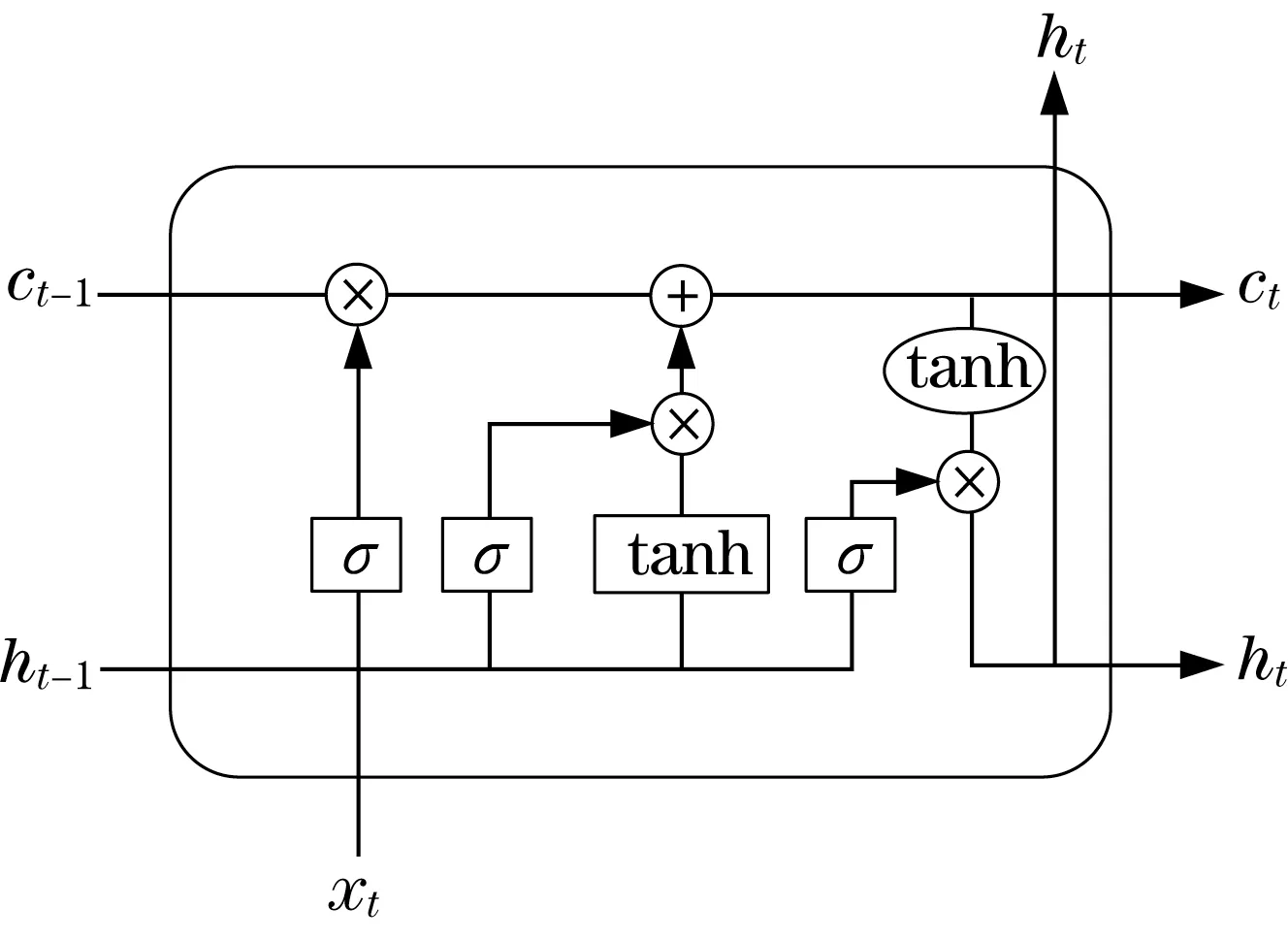
1.3 預測模型構建與評估
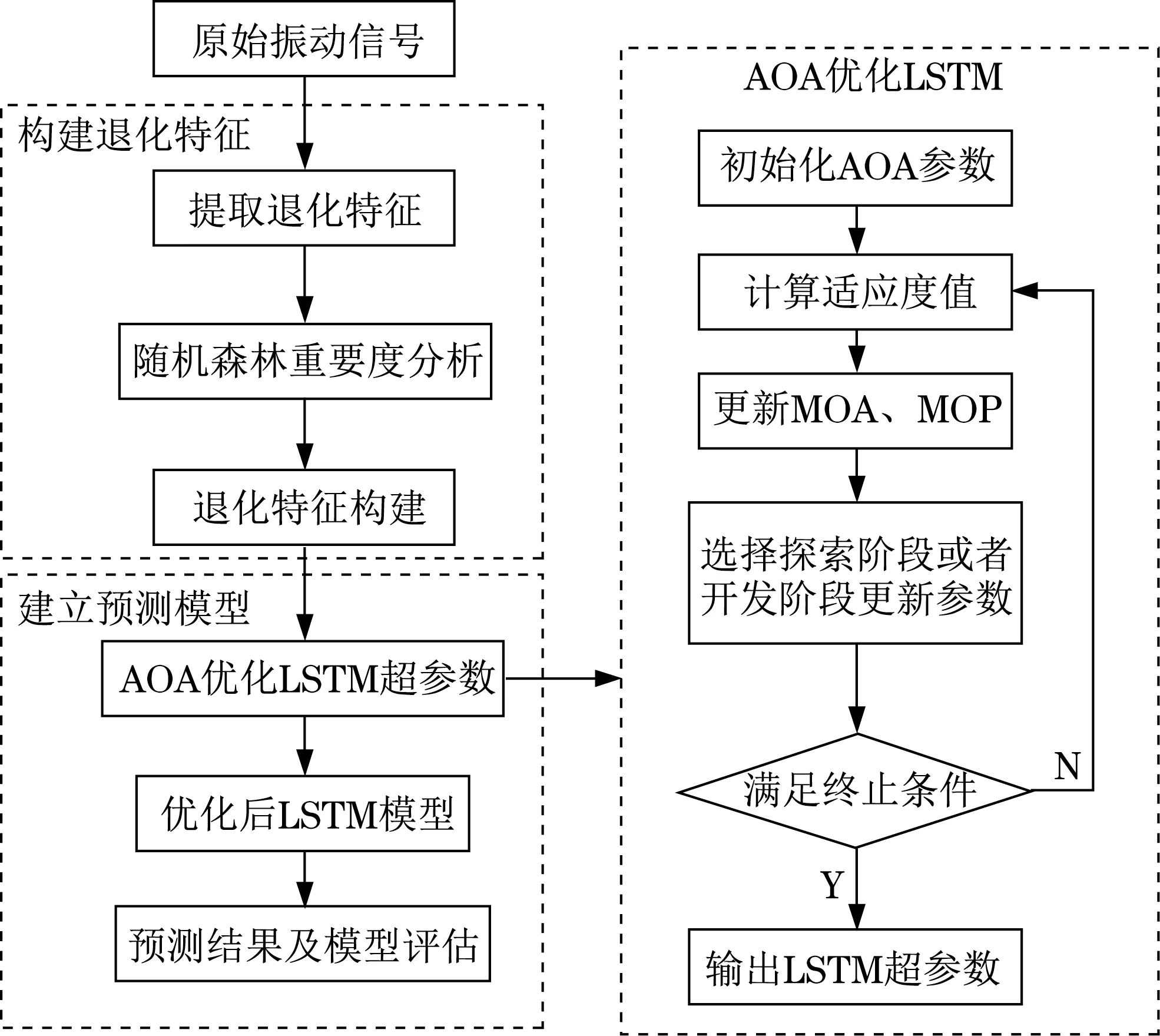
2 實例分析與驗證

3 結論

