注重變式探究 探索三新考向
——以2022年八省八校聯考第20題為例

王玉佩 張 超

(安徽省利辛縣第一中學)

圓錐曲線中的存在與探索性問題能較全面地考查考生的數學運算和邏輯推理等數學核心素養,備受命題者的青睞.因為高中數學課堂內容多,時間緊,因此數學教師對存在性問題的變式研究比較少,所以學生們在考試中遇到這類題目的時候,往往會有無從下手的感覺.基于此本文以2022年八省八校聯考(T8聯考)第20題為例對圓錐曲線中存在性問題進行了變式探究,通過實例分析,了解變式探究在培養學生核心素養中的作用,分析變式探究在日常教學中的應用情況,認識變式探究對分析問題、解決問題的價值和意義,旨在提升學生的創新能力,探索三新考向.

一、實例分析變式探究

下面以2022年八省八校聯考(T8聯考)第20題為例,引導學生通過改變題目的條件或結論等方式對新的結論進行探究,探索試題的本質,提升考生的數學運算和邏輯推理核心素養.下面分別從存在問題中角度型、向量型、面積型、直線型等類型加以探析.

【母題】(2022·八省八校聯考(T8聯考)·20)

(Ⅰ)求橢圓E的方程;

【試題分析】

考查能力:數學運算核心素養,化歸與轉化、數形結合等思想.

思維引導:(1)根據橢圓的離心率及圓的幾何性質求出a,b,即可求解.

(2)首先設直線方程,然后利用韋達定理求解即可.注意驗證Δ>0.

【解析】

設點F1,F2關于直線l的對稱點分別為M,N,由對稱性易知,線段MN為圓C的一條直徑,

所以|F1F2|=|MN|=2,即2c=2,即c=1,

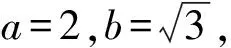
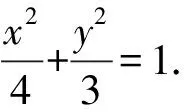
(Ⅱ)不存在.理由如下:因為原點O為線段F1F2的中點,圓心C為線段MN的中點,直線l為線段OC的垂直平分線,所以點O與C也關于直線l對稱,

因為點C(2m,4m),

又直線l為線段OC的垂直平分線,

不妨設A(x1,y1),B(x2,y2),

整理得4x2-10mx+25m2-12=0.

且Δ=100m2-16(25m2-12)>0,

所以kAC+kBC

得2x1x2-m(x1+x2)-4m2=0,

【評注】此題第(Ⅰ)問入口較難,對考生數學核心素養要求較高.通過第(Ⅰ)問也提醒我們教學中不能形成思維定勢,教學中要注重提升學生的發散思維和創新力,以便應對反套路的陌生試題.

該問有部分學生容易忽略判別式Δ>0驗證所計算的結果,最終容易導致誤判.

【變式思路】該題第(Ⅰ)問非常靈活,符合“新課程,新教材,新高考”的新要,該試題源于教材又高于教材且能有效起到試題選拔功能.

第(Ⅱ)問則主要考查學生運算水平,解題方法相對比較單一,不能很好體現“三新”要求的既要重計算,又要重思維的選拔理念.所以筆者就想能不能設置一個問題兼顧計算、思維的訓練.基于此本文從不同角度對試題進行變式探究.

【變式意義】變式后的問題力求能實現一題多解,同時兼顧計算、思維訓練.從而實現試題改編后對不同層次考生都有選拔的目的,同時通過變式研究提升學生的創新能力.

基于此,下面筆者嘗試從不同角度對試題進行變式研究.

【變式1】(知識變式)存在性問題之雙曲線型

(Ⅰ)求雙曲線E的方程;

【解析】

設點F1,F2關于直線l的對稱點分別為M,N,易知線段MN為圓C的一條直徑,

所以|F1F2|=|MN|=4,即2c=4,即c=2.

于是a2=b2=2,

(Ⅱ)不存在.理由如下:因為原點O為線段F1F2的中點,圓心C為線段MN的中點,直線l為線段OC的垂直平分線,

所以點O與C也關于直線l對稱,

因為點C(2m,4m),直線l為線段OC的垂直平分線,

不妨設A(x1,y1),B(x2,y2),

整理得3x2+10mx-25m2-8=0,

且Δ=100m2-12(-25m2-8)>0恒成立,

所以kAC+kBC

得2x1x2-m(x1+x2)-4m2=0,

即52m2=-16無解,

【評注】變式1從直線、橢圓問題變成直線、雙曲線問題,兩種題型不同視角切入,回歸一般性,得出以上關系式中參數的常值情況,可以得到以下一般性結論.該變式關鍵點是培養學生一題多解,多題一解的解題能力.

【變式2】(素養變式)存在性問題之角度型

【解題思路】

即AC⊥BC,得kACkBC=-1.

【變式3】(素養變式)存在性問題之面積型

將(Ⅱ)中條件變為“設直線l與橢圓E相交于A,B兩點,問:是否存在實數m,使S四邊形AF2BC=2S△ABC?若存在,求出實數m的值;若不存在,說明理由.”

【解題思路】

方法1:由S四邊形AF2BC=2S△ABC,得S△AF2B=S△ABC,

則只要dF2-AB=dC-AB即可.

又因為直線l:x+2y-5m=0,F2(1,0),

【評注】變式3的關鍵點:考生通過分析,由S四邊形AF2BC=2S△ABC等價轉化成dF2-AB=dC-AB.顯然該題通過方法2直接求解難度較大.

【變式4】(知識變式)存在性問題之向量型

【解題思路】

設A(x1,y1),B(x2,y2),

解法二:上同解法一,

易知點O,C,P共線,則只要kOC=kOP即可.

因為kOP≠kOC,

【評注】該變式把以斜率知識為背景變成以向量共線知識為背景,變式后的題目解法更靈活,解題思路更加清晰.通過此變式在教學中還能引導學生歸納求解字母參數值的存在性問題的解題策略:①假設→②推理與計算→若不出現矛盾,就說明滿足條件的參數值存在;若出現了矛盾,則說明滿足條件的參數值不存在.該變式關鍵點是利用韋達定理求中點P的坐標.

【變式5】(素養變式)存在性問題之定直線型

將(Ⅱ)中條件變為“設直線l與橢圓E相交于A,B兩點,弦AB的中點為M,直線OM與橢圓E相交于F,D兩點,問:是否存在直線l,使得|AM|2=|FM|·|DM|成立?若存在,求直線l的方程;若不存在,說明理由.”

【解析】

假設存在直線l,使得|AM|2=|FM|·|DM|成立,

設A(x1,y1),B(x2,y2),

整理得4x2-10mx+25m2-12=0,

解得x2=1,

因為|AM|2=|FM|·|DM|

=(|OF|-|OM|)(|OD|+|OM|),

且|OF|=|OD|

所以|AM|2=|OF|2-|OM|2,

所以直線l的方程為x+2y+4=0或x+2y-4=0.

【評注】本題(Ⅱ)問的核心在于轉化|FM|·|DM|中弦長的關系,

由|FM|=|OF|-|OM|,

|DM|=|OD|-|OM|,

且|OF|=|OD|,得|AM|2=|OF|2-|OM|2.

因此|AB|2=|FD|2-4|OM|2,

轉化為弦長|AB|,|FD|,|OM|三者之間的數量關系,易計算.

此變式目的是提升學生數學抽象、邏輯推理、數學運算等綜合素養.

二、存在性及探究性問題解題策略及三新考向思考

通過2022八省八校聯考20(T8聯考)試題分析及變式研究,結合實際教學,本人得到如下啟示:

1.圓錐曲線中存在性問題解題策略

變式探究的意義在于“解一題,會一類,通一片”,即通過研究典型試題的背景、知識、解題方法、變形延伸等,而后從中歸納總結出相似問題的解決思路和解題策略.通過變式研究不難發現存在性問題解題可通過:四個步驟,三個注意的解題策略.

步驟1:設(設點、直線)

注意①:直線斜率存在性分析、直線形式分析.

步驟2:聯(聯立→消元→韋達定理)

注意②:在求范圍、值時,注意判別式Δ檢驗結果.

步驟3:列(列(不)等式→消元)

注意③:注意列式可通過:中點型、弦長型、向量型、斜率型、目標函數型、平面幾何性質型、常見結論型等.

步驟3:求(求值、取值范圍、定值或定點、方程、存在性探究問題)

通過引導學生歸納解題思路,思考變式試題解題策略.提升學生“解一題,會一類,通一片”的綜合素養.

2.圓錐曲線中存在性問題新高考命題動向

從近兩年新高考及模考試題研究中發現,圓錐曲線中存在與探索性問題主要變化是:背景新穎化;題型多樣化;信息增量化;計算、思維兼顧化;強化數學運算、邏輯推理、直觀想象等數學核心素養的考查.

(1)背景新穎化

通過創設新穎的試題情境,創新試題呈現方式,考查學生們的閱讀理解能力,體現思維的靈活度,考查學生們的數學抽象與邏輯推理等核心素養.

(2)題型多樣化

在“三新”背景下圓錐曲線中存在性探究問題必將是新高考命題的熱點,探索存在性常考題型:數量關系型、向量型、幾何關系型、角度型等.同時由于導函數的介入,切線問題也常常被引入到綜合性的問題中.

(3)信息增量化

圓錐曲線中存在性試題在試卷中難度有增加的趨勢,其目的不僅要對圓錐曲線的基本概念、方法、技能方面進行考查,還要對思維方面進行考查.所以存在性試題的命制既要重視計算,又要兼顧思維.像2022八省八校聯考(T8聯考)第20題第(Ⅰ)問信息量增加、方式更為靈活.

(4)計算、思維兼顧化

圓錐曲線存在性問題需要熟練掌握圓錐曲線的基本知識和基本技能,所以我們在教學中要重視計算經驗積累,同時也要將試題合理的變式,提升發散思維的能力.