系留氣球升空動力學仿真

王永林,夏 雨

(中國電子科技集團公司第三十八研究所 浮空平臺研發中心,合肥 230088)

0 前言

系留氣球是一種利用球體內充入密度小于空氣的氣體(如氦氣、氫氣等)所產生的靜浮力來克服其自身質量的浮空飛行器,它依靠系留纜繩實現在空中長時間定點滯空。系留氣球具有連續滯空時間長、生存能力強、研制與使用成本低、維護方便、能搭載多種任務系統等特點,在通訊、遙測、偵察、干擾和預警等領域有著廣泛的應用。系留氣球基本有四種典型運動狀態:滯空工作、地面系留、拉索收放、升空與回收。目前國內外對氣球動力學仿真主要集中在前三個狀態[1-5],對于升空與回收研究較少,且主要集中在球形系留氣球[6-7]。本文針對艇形氣球(帶尾翼)建立升空動力學模型,通過不同風速、不同升空速度下的仿真示例,分析了氣球上升過程中的動力學特性。

系留氣球系統包括三個部分:氣球、纜繩和地面錨泊設備,系留氣球系統如圖1所示。系留氣球系統的運動與常規飛機/飛艇差別較大,需要聯合氣球、纜繩和地面錨泊轉動機構進行動力學仿真。

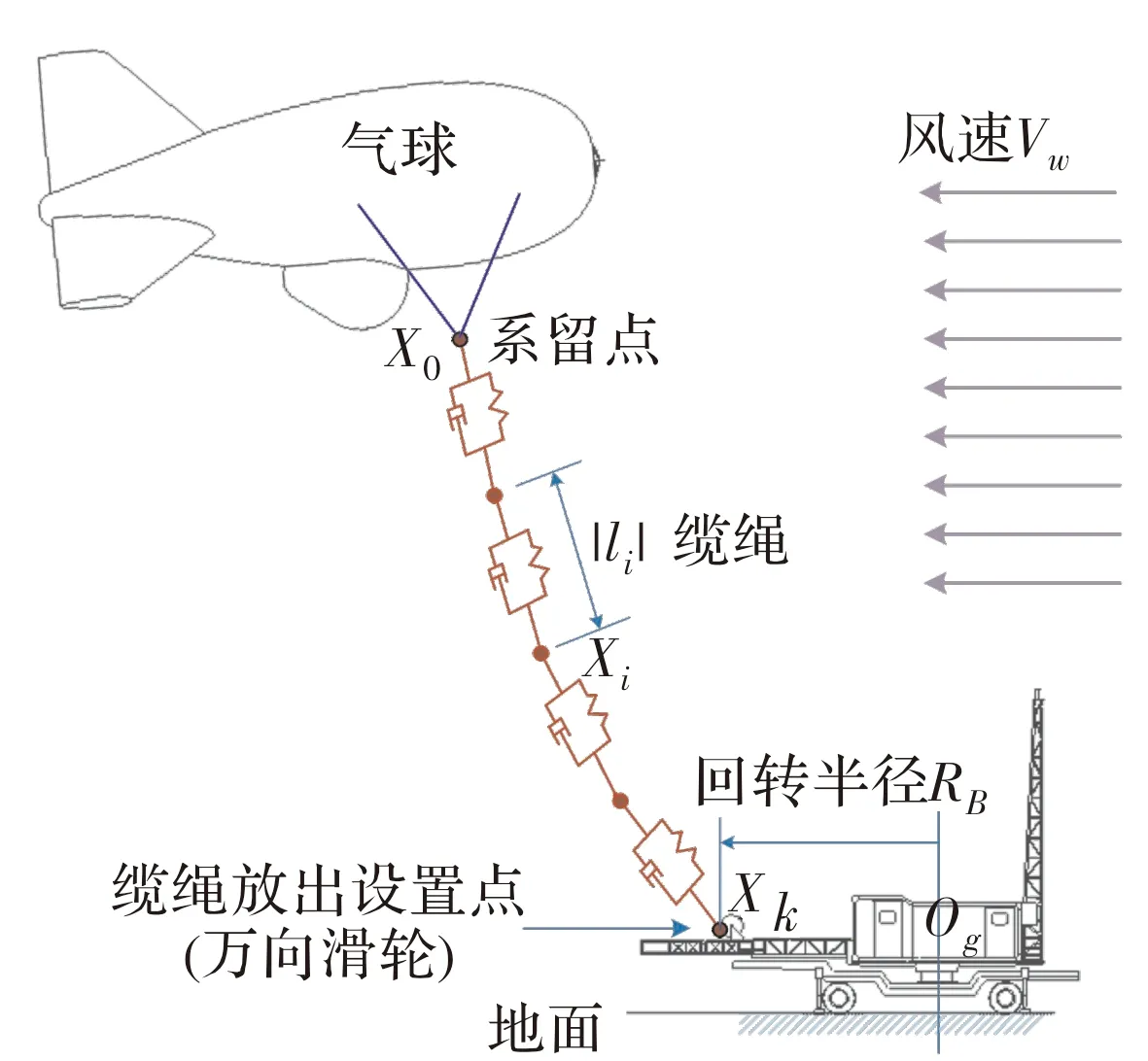
圖1 系留氣球系統

1 氣球動力學方程

圖2 系留氣球受力示意圖

氣球的動量p與動量矩L可表示為:

p=m(VK+ω×RG)

(1)

L=Iω+mRG×VK

(2)

其中:m是氣球總質量(包括囊內氣體);VK是地速;ω是氣球角速度;RG是重心坐標;I是氣球轉動慣量。

根據動量和動量矩定理,剛體氣球的力和力矩六自由度動力學方程可表示為:

(3)

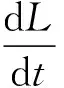
(4)

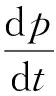
F=FG+FB+FT+FA

(5)

M=MG+MB+MT+MA

(6)

其中:FG、MG分別為重力、重力矩;FB、MB分別為浮力、浮力矩;FT、MT分別為纜繩張力、張力矩;FA、MA分別為氣動力、氣動力矩,包括氣動附加慣性力/力矩。

2 纜繩動力學方程

2.1 纜繩動力學方程

纜繩建模目前常用“彈簧-阻尼器-質點”模型[2]。彈簧-阻尼器-質點模型受力示意圖如圖3所示,纜繩分成k節直的彈性段,各段之間由萬向球節連結,纜繩質量集中在節點上。第i節點的坐標向量表示為Xi,X0為纜繩與氣球連結點,即氣球系留點,Xk附著于萬向滑輪。

圖3 彈簧-阻尼器-質點模型受力示意圖

纜繩張力沿其直彈性段方向,其值|Ti|可表示為:

(7)

其中:|Ti|是纜繩張力大小;A是纜繩橫截面積;E是纜繩彈性模量;η是纜繩阻尼系數。

至于房產交易稅等其他支出，易居智庫研究總監嚴躍進則認為，從公攤面積角度看，確實不應重復收繳此類稅費，建議未來房產交易稅費、供暖費等統一按照套內面積收取。

εi的表達式為:

(8)

其中,|li|與|liu|分別為第i段纜繩拉伸與未拉伸長度。由于柔性纜繩受拉不受壓,當|Ti|<0時,令|Ti|=0。

纜繩段矢量li的表達式為:

li=Xi-Xi-1

(9)

Ti的表達式為:

(10)

纜繩動力學方程一般建立在地面坐標系下。忽略空氣浮力、纜繩第i節質點的三自由度平動,動力學方程可表示為:

miXi=Ti+1-Ti+Gi+Fi

(11)

其中:mi是第i節點的質量;Gi是第i節點的重力;Fi是第i節點的氣動力;Ti、Ti+1分別是第i、i+1直彈性段的纜繩張力。

2.2 氣球升空纜繩模型

纜繩長度、段數增加框圖如圖4所示,纜繩初始分為k段,氣球升空過程中,1～(k-1)段纜繩長度|l1u|、|l2u|、…、|l(k-1)u|保持不變,第k段纜繩長度|lku|可變(其中下標u表示纜繩未受拉伸)。第j個仿真時間步長Δtj內,節點Xk處放出纜繩長度設為|Δlju|,即第k段纜繩長度增量為|Δlju|。當|lku|長度大于|lkuM|(第k段規定的最大長度),則纜繩段數增加1,繼續保持最下端纜繩段長度可變,其余纜繩段長度保持不變。按此規則,隨著纜繩的放出,纜繩段與節點不斷增加。

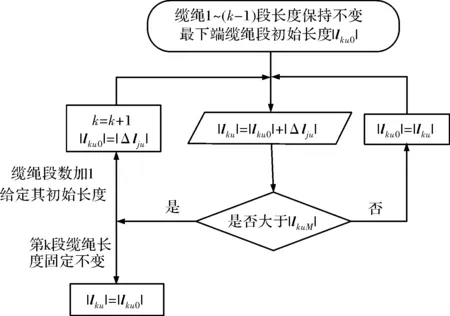
圖4 纜繩長度、段數增加框圖

3 仿真算例

根據建立的系留氣球升空力學模型,進行兩組升空動力學仿真:不同放纜速度下的升空仿真和不同風速下的升空仿真。氣球系統的部分參數:氣球體積3 300 m3,初始纜繩長度150 m,初始纜繩分段數3,單段纜繩最大(未拉伸)長度:50 m。仿真曲線中所給的氣球高度/速度均為氣球主氣囊形心處的高度/速度。仿真工具為本單位開發的Aerostat Simulation仿真軟件。

3.1 不同放纜速度下的升空仿真

氣球在不同放纜速度下升空性能對比如圖5所示。風速、放纜速度設定:穩定風速6 m·s-1;放纜速度0.5 m·s-1、1.0 m·s-1、1.5 m·s-1、2.0 m·s-1。圖5(a)為纜繩放出速度-時間圖,包括啟動、勻速放出、停止三個階段。圖5(b)為纜繩總長度-時間圖。圖5(c)為纜繩分段數-時間圖,由于本文中纜繩段最大長度設定為50 m,隨著纜繩不斷放出,纜繩分段數便會不斷增加。圖5(d)為氣球高度-時間圖。

纜繩頂端張力-時間圖如圖5(e)所示,纜繩底端張力-時間圖如圖5(f)所示,由圖5(e)、圖5(f)可以看出,隨著升空過程中纜繩重量的增加,底端張力亦逐漸減小,頂端張力變化較小。

氣球升降速度-時間圖如圖5(g)所示,可以看出,在給定的風速條件下,氣球的升降速度接近纜繩放出速度。氣球空速-時間圖如圖5(h)所示,氣球空速由風速、氣球地速合成而得,由于氣球升空速度基本為垂直上升速度,且遠小于水平風速,所以上升過程中氣球空速的值約等于風速值。

俯仰角-時間圖如圖5(i)所示,迎角-時間圖如圖5(j)所示。可以看出,氣球的初始迎角/俯仰角為6,纜繩放出后,氣球上升導致的空速分量使得氣球迎角減小、俯仰角增大。對于1 m·s-1放纜速度下的升空過程中,迎角穩定在-2.0°附近,俯仰角穩定在7.5°附近。纜繩停止放出后,迎角/俯仰角逐漸恢復到6°附近。

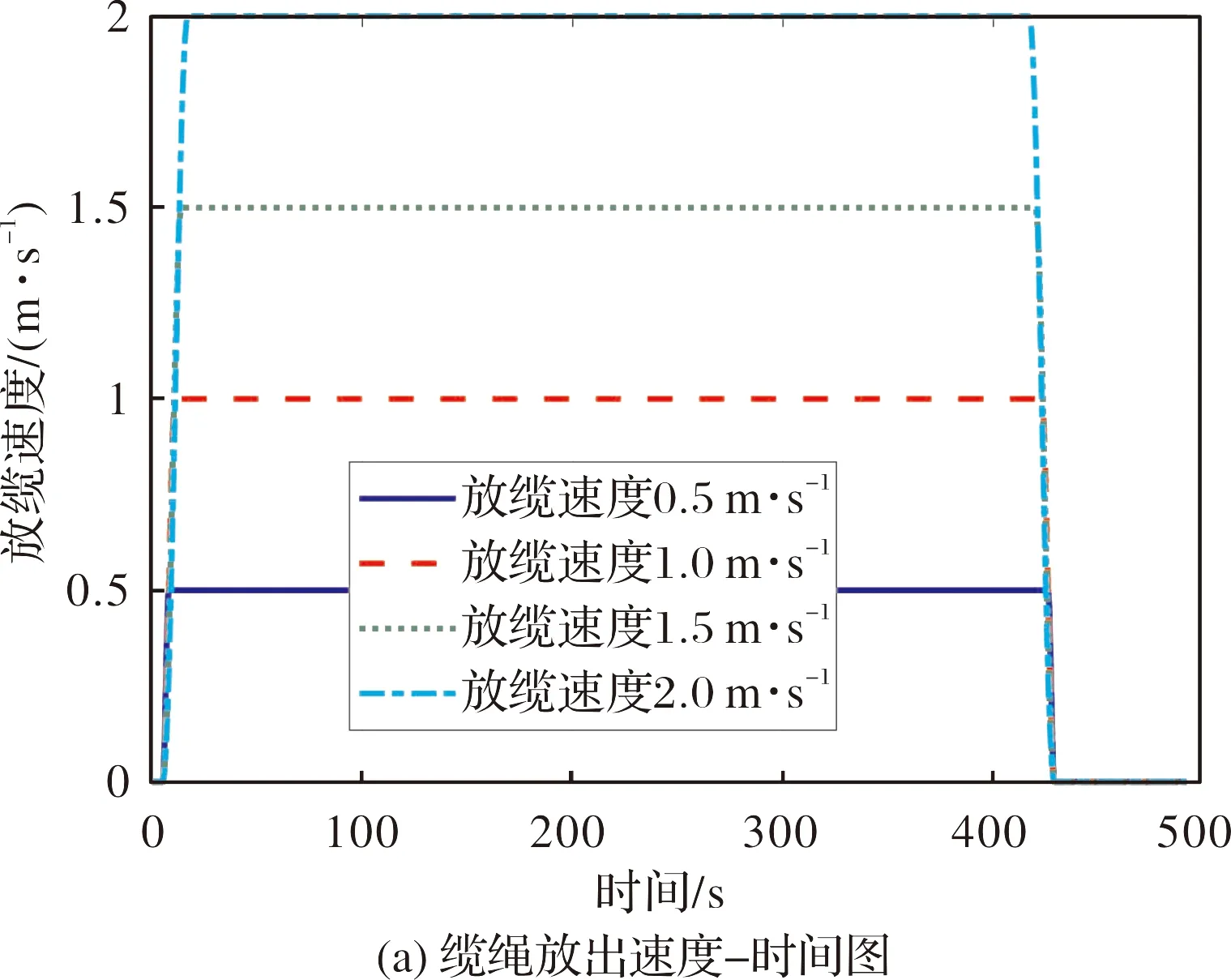
圖5 氣球在不同放纜速度下升空性能對比

綜上可得出:放纜速度越快,氣球的上升速度越快、迎角越小、俯仰角越大、纜繩張力越小。

3.2 不同風速下的升空仿真

氣球在不同水平風速下升空性能對比如圖6所示。風速、放纜速度設定:穩定放纜速度1 m·s-1;穩定水平風速3 m·s-1、6 m·s-1、9 m·s-1、12 m·s-1。由仿真曲線可以看出,纜繩放出速度穩定階段,風速越大,迎角越大、俯仰角越大、纜繩張力越大。

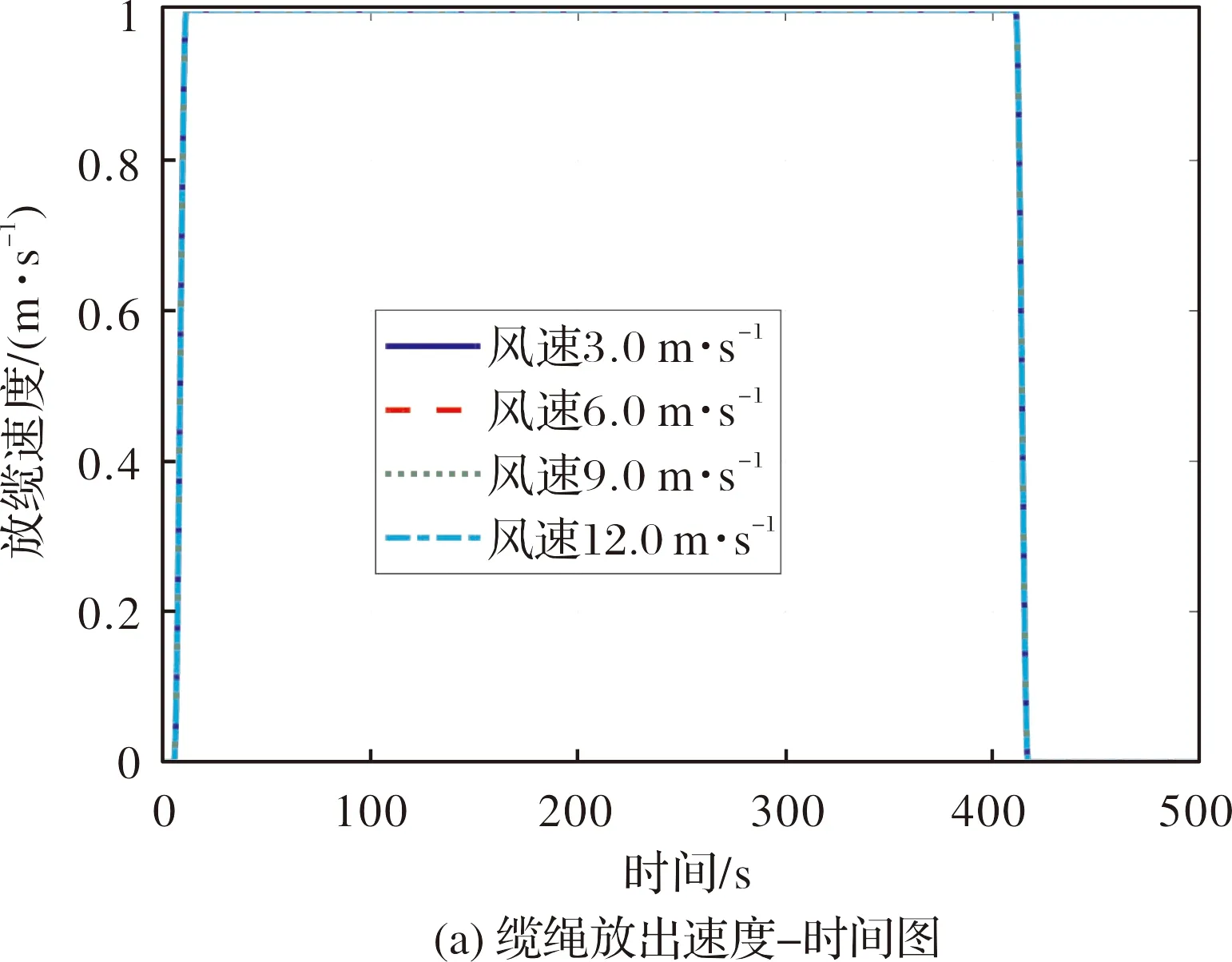
圖6 氣球在不同水平風速下升空性能對比

4 結論

系留氣球升空動力學仿真可以為氣球系統設計提供理論依據,也可以為外場放飛決策與放飛數據研究提供一種分析工具。由仿真示例可以得出:升空過程中,放纜速度增大則氣球俯仰角增大,迎角、纜繩張力減小;升空過程中,風速增大則迎角、俯仰角、纜繩張力均增大。