心電信號抑噪算法的研究
梁伯虎 石翠萍 于泓博

摘要:基于卡爾曼濾波和平滑濾波相融合的方式,獲得濾除工頻干擾和肌電干擾的解決方案。平滑濾波主要濾除工頻干擾,將平滑濾波后的心電信號以自回歸模型的方式進行心電信號建模,并且導入卡爾曼濾波的狀態方程和觀測方程,完成卡爾曼濾波,可以有效地濾除肌電干擾。根據仿真實驗的結果,基本實現從心電信號中濾除工頻干擾和肌電干擾。
關鍵詞:心電信號;平滑濾波;卡爾曼濾波
一、前言
由于人們生活節奏的加快,心臟疾病成為威脅人類健康的一大殺手。心電信號能客觀反映心臟的生理信息,因而成為診斷和治療心臟疾病的重要參考依據。但是在采集心電信號時,往往受到患者身體狀況、周邊環境和采集儀器等因素的影響。這些干擾會使心電信號的信噪比被降低,發生信息丟失或產生虛假信息[1]。因此,本文研究基于卡爾曼濾波和平滑濾波的心電信號抑噪算法,以濾除噪聲而又不失真的保留原始信號的細節特征為目標,設計相對高效的濾波系統。
二、抑噪算法的總體設計
選擇心電信號的仿真數據。采用麻省理工學院和Beth Israel醫院聯合提供的MIT-BIH心律失常數據庫的心電數據作為仿真數據。MIT-BIH庫的心電數據權威而且充分[2]。
仿真心電觀測信號。在分析心電信號的特點,以及對噪聲和干擾充分認識的基礎上,選擇兩種對心電信號影響較大而且較難濾除的噪聲—工頻干擾(一種幅頻特性接近于頻率是50Hz的正弦波干擾)[3]和肌電干擾(一種近似于白噪聲的干擾)[4],疊加在MIT-BIH庫的心電數據上,仿真心電觀測信號。
針對心電信號中存在的工頻干擾,采用平滑濾波算法進行濾除。
建立心電信號的數學模型。將平滑濾波后的心電信號,基于遞推最小二乘算法建立心電信號的自回歸模型,推導出卡爾曼濾波算法的狀態方程和觀測方程。
針對心電信號中存在的肌電干擾,采用卡爾曼濾波算法進行濾除。
對卡爾曼濾波和平滑濾波后的心電數據進行分析。采用心電圖各個波段的可識別度進行定性評價指標;采用信噪比、相關系數和均方誤差作為定量評價指標。
(一)心電信號的仿真數據
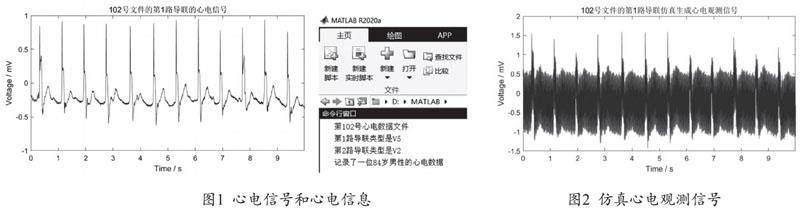
本文選取MIT-BIH庫中第102號心電數據的第1路導聯的前3600個采樣點作為仿真數據,稱為凈信號。利用MATLAB軟件仿真出心電信號和心電信息,如圖1所示。
(二)仿真心電觀測信號
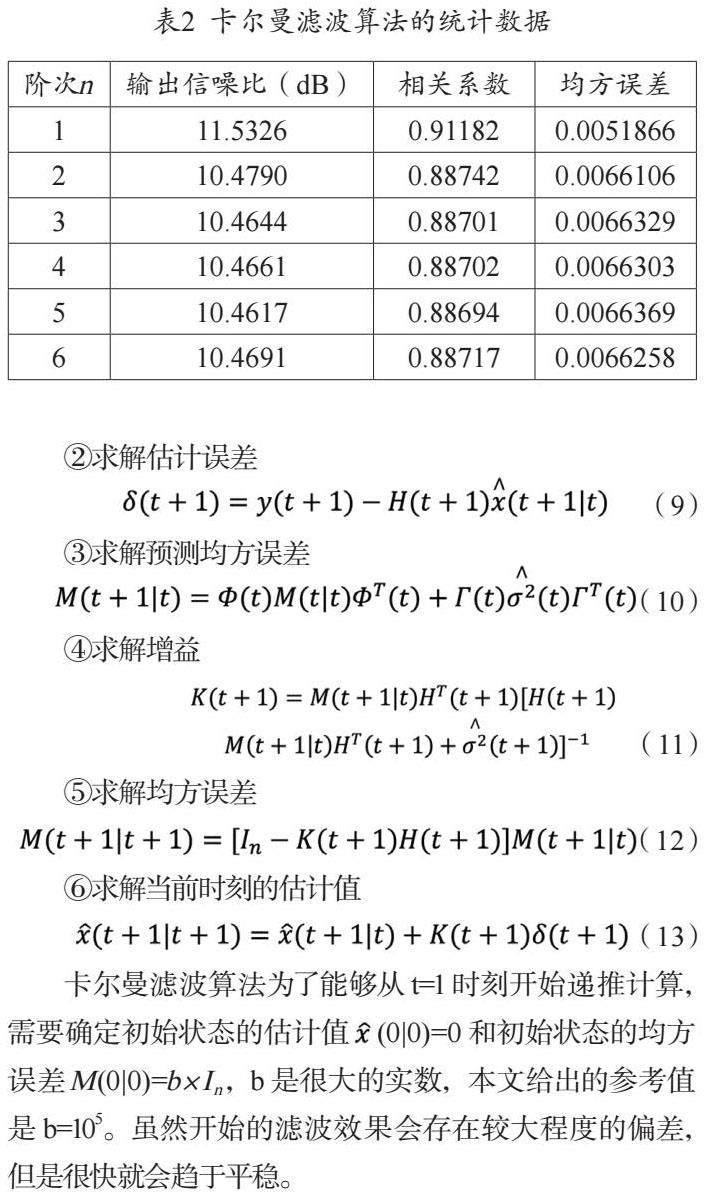
在充分掌握工頻干擾和肌電干擾特點的前提下:以頻率是50Hz,幅值是心電信號峰—峰值乘以0.5的正弦波作為工頻干擾的仿真噪聲源;以均值為零,方差為心電信號峰—峰值的平方乘以0.01的高斯噪聲作為肌電干擾的仿真噪聲源,將這兩種噪聲源同時疊加在凈信號上,以實現心電觀測信號的數學仿真,如圖2所示。
(三)平滑濾波算法
平滑濾波算法的具體操作步驟如下:采用當前時刻的心電數據和當前時刻之后的M-1個時刻的心電數據,做數學期望,將得到的數據作為當前時刻濾波后的心電數據。
心電信號的采樣頻率是360Hz,工頻干擾的頻率是50Hz,所以工頻干擾的一個周期影響心電信號的7~8個采樣點。而在一個工頻干擾的周期內,它的數學期望接近于零。因此,平滑濾波算法M值的參考取值范圍在7~8之間。通過實驗對比不同M值對平滑濾波后的心電信號的影響,根據表1進行定量分析:當M=7時,濾波后的心電信號輸出信噪比和相關系數最高,均方誤差最小,說明最接近于凈信號。所以,當M=7時,平滑濾波效果最好。
(四)心電信號的自回歸模型
將平滑濾波后的心電信號建立自回歸模型。
心電信號的自回歸模型表達式:
n是自回歸模型的階次。
在已知心電信號的情況下,求解心電信號的自回歸模型參數就歸結為求解自回歸模型的階次和加權系數以及系統噪聲。
1.階次的確定
通過仿真實驗,在后文給出合適的階次。
2.加權系數的確定
遞推最小二乘算法能夠根據輸入數據進行自回歸模型加權系數的調整和修正,使其最大限度地接近于真實值,它的收斂速度和健壯性都比較好,計算量和數據存儲量也相對較小,而且對心電信號的先驗統計特性要求不高。因此,本文采用遞推最小二乘算法對心電信號的自回歸模型進行加權系數的確定。遞推最小二乘算法公式如下:
初值P(0)=a×In,a是很大的實數,本文給出的參考值是a=105,In是n階的單位向量;θ (0)=0;y(t)=0 (t≤0)。
通過式(2)和式(3)的遞推計算,可以得到各個時刻心電信號在自回歸模型中的加權系數,并且截取收斂后的ai值作為所有心電信號的加權系數。
3.噪聲方差的確定
綜上所述,心電信號自回歸模型的參數可以根據以上式子全部遞推得到。完成整個建模的過程,為后續卡爾曼濾波計算奠定基礎。
(五)卡爾曼濾波算法
本文采用卡爾曼濾波算法濾除肌電干擾。卡爾曼濾波算法將系統的狀態方程和觀測方程相結合,隨著下一時刻心電信號的到來,能夠比較準確地計算出下一時刻系統的估計值。狀態方程是描述狀態變化規律的方程,它記錄了相鄰時刻狀態轉移的變化規律。觀測方程是描述不同時刻心電信號變化的方程。卡爾曼濾波算法不斷地通過“預測—實測—修正”對帶有噪聲干擾的心電信號進行遞推,得出每一時刻的最優估計值,可以有效地消除噪聲的干擾。
1.卡爾曼濾波算法的狀態方程和觀測方程
心電信號的自回歸模型可以通過推導,得到卡爾曼濾波算法的狀態方程和觀測方程。
2.卡爾曼濾波算法的步驟
利用得到的自回歸模型、狀態方程和觀測方程,帶入下面公式,完成卡爾曼濾波[5]。
卡爾曼濾波算法為了能夠從t=1時刻開始遞推計算,需要確定初始狀態的估計值 (0|0)=0和初始狀態的均方誤差M(0|0)=b×In,b是很大的實數,本文給出的參考值是b=105。雖然開始的濾波效果會存在較大程度的偏差,但是很快就會趨于平穩。
根據常用自回歸模型的階次n=1~6的取值范圍,分別用上述方法進行卡爾曼濾波仿真。濾波后的統計數據如表2所示。
從表2可以看出:當n=1時輸出信噪比最大,相關系數最高,均方誤差最小,說明此時對噪聲的抑制能力最強,輸出信號與凈信號的相關程度最高,輸出信號最接近于凈信號。所以,由實驗結果得出,當自回歸模型的階次等于1時,卡爾曼濾波效果最好。
(六)實驗分析
為了說明濾波算法對不同的心電信號都有很好的濾波效果,本文利用MIT-BIH庫中的心電數據,進行了充分的仿真實驗。根據實驗結果:圖3左圖是濾波后的心電信號,針對此波形與凈信號(圖1)進行定性的對比分析,可以得出濾波算法基本濾除了干擾造成的毛刺;圖3右圖是從濾波后的心電信號中任意截取一小段心電信號,可以看出較完整地保留了凈信號各個波段的細節信息;從表3濾波前后性能指標統計的平均值,經過定量分析可以得出,濾波后的平均輸出信噪比和相關系數得到明顯的提升,說明濾波后的輸出信號與凈信號的相關程度比較高;濾波后的平均均方誤差有明顯的下降,說明濾波后的輸出信號比較接近于凈信號。因此本文所采用濾波算法的輸出數據與凈信號吻合度相對較高,證明濾波算法對噪聲的抑制能力較強。綜上所述,卡爾曼濾波和平滑濾波能夠比較有效濾除工頻干擾和肌電干擾。
三、結語
隨著醫療技術的不斷發展與革新,加強對心電信號抑噪算法的研究愈發顯得格外重要。本文使用MIT-BIH庫的心電數據作為仿真實驗的數據,對心電圖各個波段的可識別度作定性評價,并且以信噪比、相關系數和均方誤差作為濾波算法的定量評價指標,充分驗證了濾波算法的有效性。 同時也希望通過相關研究工作的開展,更好地助力于今后濾除工頻干擾和肌電干擾工作的升級。
參考文獻
[1]趙博特.心臟病史與首發卒中預后的相關性研究[J].中國臨床保健雜志,2022,25(5):619-623.
[2]梁伯虎.基于Matlab的MIT-BIH心電信號讀取與波形顯示的實現[J].中國電子商務,2011(11):113.
[3]孫京霞.一種抑制心電信號50Hz工頻干擾的改進Levkov方法[J].航天醫學與醫學工程,2000,13(3):1-5.
[4]張長勝.AN-CEEMD算法對心電信號中肌電干擾的降噪研究[J].昆明理工大學學報(自然科學版),2020,45(6):60-66.
作者單位:齊齊哈爾大學通信與電子工程學院

