腐蝕減薄柱形殼軸壓屈曲特性研究

王黎輝，馮 杰，朱永梅,2

(1.江蘇科技大學 機械工程學院，江蘇 鎮江 212003；2.江蘇省船海機械先進制造及工藝重點實驗室，江蘇 鎮江 212003)

0 引 言

柱形殼因為其結構簡單承載能力好而應用廣泛，其中海洋平臺樁腿是其應用最多的領域之一[1]。海水具有較強的腐蝕性，海水腐蝕破壞在海洋環境中十分常見，如深海管道、遠洋船體和海洋平臺樁腿等，一直受到腐蝕危害。海洋平臺樁腿因為常年在海洋環境下工作，樁腿的外壁會產生局部腐蝕，嚴重情況下會導致樁腿發生非線性屈曲，影響海洋平臺的穩定與安全[2]。

在腐蝕的情況下柱形殼的軸向臨界載荷的計算十分復雜。Philippe[3]在外壓圓柱殼缺陷敏感性研究領域中，證明幾何缺陷不容忽視。Blachut[4]利用有限元方法研究了許多不同形狀缺陷對圓柱殼屈曲特性的影響，其中包括了樣條形缺陷和矩形凹陷等。Arbelo 等[5]在復合材料圓柱殼鄰域進行了研究，主要研究多點凹陷的復合材料對圓柱殼極限載荷產生的影響，最終發現多點擾動載荷更加保守。Kreilos[6]以及Virot 等[7]分別從理論和試驗的角度研究了局部凹坑缺陷對軸壓圓柱殼屈曲強度的影響。MacKay 等[8]在腐蝕損傷對穩定性產生的影響進行了研究，通過設計鋁鋼瓶試驗，發現人為制造的減薄區域在失穩過程中產生應力集中，其抗壓能力與人為減薄厚度相關。Inoue 等[9]在對102 號直管管材破壞行為影響的要素研究中，利用人為壁厚減薄模擬海洋腐蝕損耗，對減薄的形狀和位置等因素進行了研究。這些研究局部腐蝕的對象多種多樣，然而目前軸壓圓柱殼研究中，探索局部腐蝕缺陷對柱形殼屈曲特性有何影響的研究鮮見報道。

本文利用壁厚減薄模擬海洋中柱殼的腐蝕損失，嘗試加工了4 種不銹鋼局部減薄柱形殼試驗模型，以及一個未進行減薄加工的完好柱殼試驗模型，對這些試驗模型進行三維光學掃描、超聲波無損測試和軸向外壓試驗，并采用數值方法分析局部減薄殼體的屈曲特性，考察局部減薄缺陷位置、局部減薄缺陷形狀對殼體的影響。

1 材料與方法

研究對象是海洋平臺的樁腿，該樁腿的結構是圓柱殼，實際尺寸如下：每段圓柱殼高度為4 500 mm，一共由13 段構成，每段圓柱殼的厚度為48 mm，直徑為2 800 mm，對其中一段圓柱殼進行40∶1 的縮小，得到本文的研究對象。其尺寸如下：外徑D=70 mm，高度或長度H=112.5 mm，厚度T=1.2 mm，T/R=0.034，根據Zhang 等[10]對耐壓殼的研究，T/R=0.05 為厚殼、薄殼的分界值。如圖1 所示，不銹鋼柱形殼的5 種實物模型分別為未減薄的完好柱殼（PE），中部圓形減薄柱殼(RC)，端部圓形減薄柱殼（RE），中部方形減薄柱殼（SC），中部長方形減薄柱殼（OC）。對于減薄缺陷處，減薄的體積為柱殼總體積的1%，本文研究了3 種減薄形狀，分別為：直徑d=20 mm 的圓形、邊長為17.72 mm 的方形和長寬分別為31.4 mm，10 mm的長方形。減薄處厚度t=0.7 mm，即與原來的壁厚相比t/T約為60%的厚度，減薄處的面積都近似相等于314 mm2。

減薄缺陷幾何中心距底端長度為L,L在圖1 四個減薄模型中分別為56.25 mm，10.5 mm，56.25 mm，56.25 mm，與柱殼高度相比T/H分別為50%，9.33%，50%，50%。這些缺陷形狀是指柱殼展開后表面上的形狀，與直接投影至柱殼有所區別。

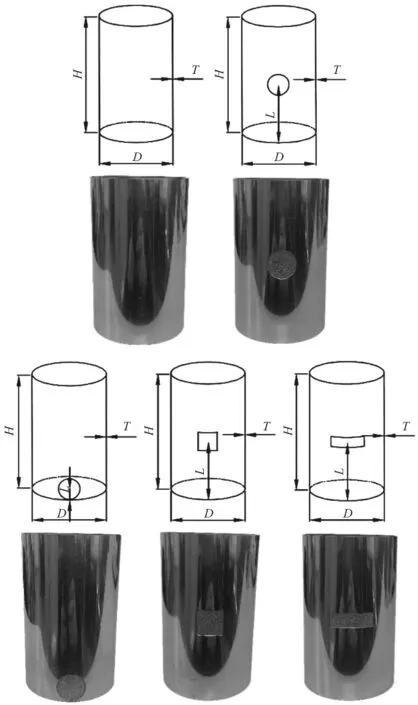
圖1 柱形殼模型圖Fig.1 Cylindrical shell model drawing

共有5 種類型的試件，分別稱為PE，RC，RE，SC，OC，為保證數據可重復性，每個試件均制作了4 個，分別編號1，2，3，4，共20 個試件。這樣就可以通過試驗對局部減薄柱殼的屈曲特性進行研究。

1.1 加工與測試

材料是一種奧氏體不銹鋼，其無明顯屈服極限，因此以產生0.2%殘余變形的應力值作為其屈服極限。測試3 次，0.2%殘余變形應力值分別為452.00 MPa，458.85 MPa 和460.15 MPa，其均值屈服強度σyp=457 MPa，楊氏模量E=193 GPa，泊松比μ=0.281。試驗柱形殼利用激光從長圓柱鋼管上切割下來，相較于傳統砂輪切割有更小的誤差，為軸壓實驗提供了更好的軸心受壓條件。柱形殼上的局部減薄是采用電火花加工方式實現，其原理是電蝕作用蝕除導電材料，利用此種加工方法在良好的加工條件下可以獲得相對較好的表面粗糙度[11]。

采用Cronos 3D 光學掃描儀測量每個試驗殼體外表面形狀，獲取表面點云的坐標數據，用具有三維誤差檢測功能的軟件GOM Inspect 軟件對掃描結果進行處理。軟件會將光學掃描儀的點云數據轉換為三維網格數據，之后對比網格數據和CAD 名義尺寸數據進行圓柱殼的表面誤差檢測。之后，采用超聲波測量儀PX-7 對6 個柱形殼進行厚度測量，沿模型周向均分10 組，每組沿軸向測量7 個點位（落入缺陷處的點不計入結果），減薄缺陷內等間距取三橫三豎的9 個交點并測量其厚度，測量結果列于表1。

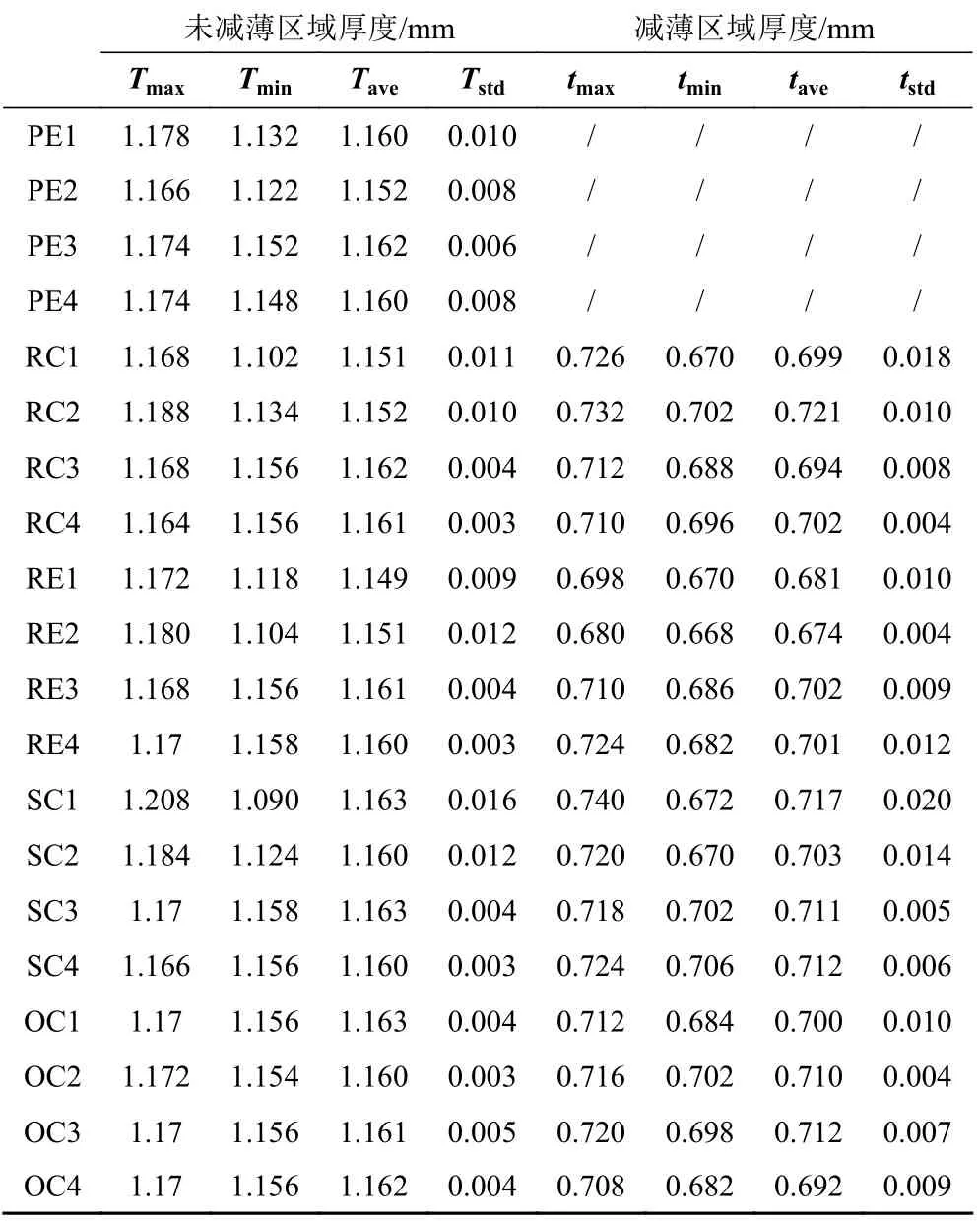
表1 模型壁厚測量結果Tab.1 Measured wall thickness data for specimens

形狀和壁厚測量之后，對柱殼試驗模型進行軸向壓力測試，獲取殼體屈曲載荷和最終失穩模式。試驗采用萬能壓縮試驗機，試件是由激光切割而成，兩端面非常平整，壓縮試驗機平臺水平放置一個圓盤，將柱殼試件放置于圓盤上。將壓力機壓頭慢慢調至剛與柱殼的上端部接觸后，開始正式壓縮試驗。壓頭下降的速率為1 mm/min，壓縮變形量設置為4 mm。

1.2 數值模型

按照測量尺寸采用有限元法對20 個試驗柱形殼進行數值建模。采用ANSA 軟件進行數值模型網格劃分，單元數量根據網格收斂性分析確定。單元的類型主要使用四邊形殼通用單元S4，部分使用三角形通用殼單元S3，使用Abaqus 軟件進行處理分析。

首先，在Abaqus 軟件中進行線性屈曲分析，本次材料使用的是奧氏體不銹鋼，這種材料的各向異性不明顯，所以在仿真過程中不予特殊考慮。不銹鋼材料參數定義為：楊氏模量E=193 GPa，泊松比μ=0.281，屈服強度σyp=457 MPa。厚度設置為每個殼體測量結果的平均值，創建2 種不同厚度截面，將2 種厚度截面分別指派給無缺陷和有缺陷區域。柱形殼軸壓屈曲分析要在殼體端部中央設置一個參考點，該參考點設置在距離端部0.01 mm 處，這種設置方法有利于施加載荷，并且會減少應力集中。將該參考點與柱形殼端部殼體采用剛體約束進行綁定。初始載荷集中力施加在參考點上，初始載荷值為100。根據周通等[12]的研究，相應的約束定義為：底端6 個自由度均限制，如圖2 所示。參數設置為：特征值數量為6，每次迭代向量數量為12，將迭代步數為設置為300。完成后獲其一階屈曲模式。

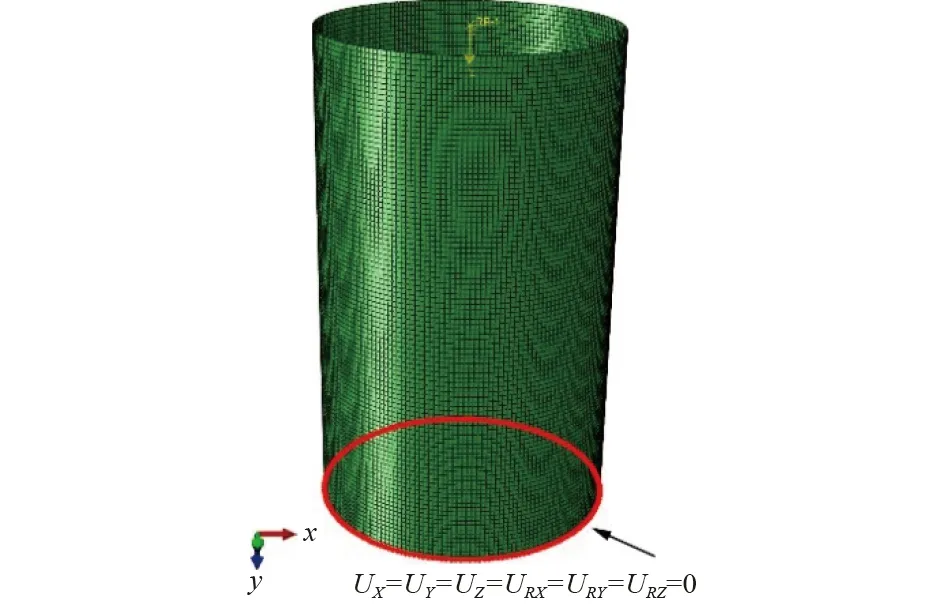
圖2 有限元模型Fig.2 Finite element model

線性屈曲分析僅能分析理想情況下線彈性殼體的屈曲特性，無法對非線性特性進行分析[13]。為了得到更為準確的結果，進行非線性屈曲分析。在Abaqus 軟件中，使用其Riks 弧長法進行非線性屈曲分析，理想彈塑性模型如下式：

式中：E為材料楊氏模量；σyp為材料屈服強度。

在分析步模塊中利用Riks 弧長法進行非線性屈曲分析，其基本參數為：初始弧長0.01 mm，最大弧長0.01，最小弧長1×10-50mm，總弧長1 mm 的最大迭代步數為3 000。初始載荷為50 000，此外采用和線性屈曲分析相同的邊界條件。

由此可以獲得柱形殼模型非線性屈曲過程的平衡曲線，此曲線極值點即為臨界屈曲載荷。

2 結果分析與討論

2.1 測量結果分析

圖3 為20 個柱形殼的掃描模型相對于理想模型的誤差云圖。誤差大小的范圍可以從右側數值帶數據看出，誤差頻數分布情況可以從右側曲線看出。圖中減薄柱殼的誤差比完好柱殼的誤差要大，且減薄柱殼的上偏差多集中在減薄區域的上下兩側，其可能和減薄缺陷的加工過程相關，總體上20 個試件的誤差基本在-0.1～0.3 mm 之間。

圖3 柱殼掃描模型及其幾何誤差云圖Fig.3 Cylindrical shell scanning model and geometric error cloud

2.2 試驗結果分析

計算機通過數據采集系統在試驗過程中采集數據，本次試驗中主要采集位移與載荷數據，試驗的位移量為0～4 mm。如圖4 所示，以第1 組5 個柱形殼為例，根據它們的數據進行位移載荷圖的繪制。

圖4 局部減薄柱殼與完好柱殼擁有相似的位移-載荷曲線。所有的曲線都有上升階段、屈曲臨界點和屈曲失穩階段。由于此種類型的不銹鋼具有較高的韌性，故沒有破壞階段。開始時載荷并沒有出現迅速增長，導致這種現象的原因可能是殼體上下兩端存在的長度缺陷。隨著位移的繼續增大，載荷上升出現屈曲臨界點。經過臨界點后，載荷開始緩慢降低。

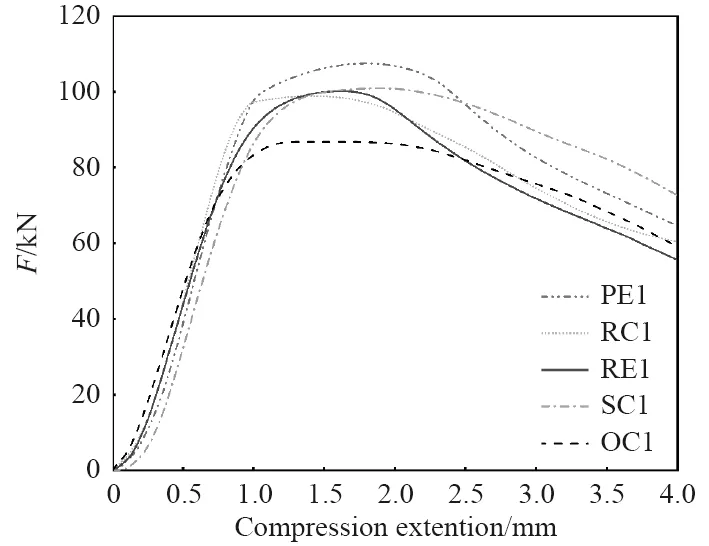
圖4 第一組柱殼試驗載荷位移曲線Fig.4 Load displacement curves of the first set of cylindrical shell tests

表2 為5 種柱殼試驗測得的最大屈曲載荷數值，各組柱殼試件的試驗數值具有良好重復性。由表2 可見，未減薄完好柱殼的屈曲載荷明顯大于其他4 種局部減薄柱殼，最大差值達到20.69 kN，表明腐蝕減薄在會很大程度上削弱了柱殼的承載能力；在4 個完好柱殼中，根據作用在截面平均壁厚上的力，求得的壓強均未達到材料的屈服強度457 MPa，還未達到塑性失效的范圍，所以本次試驗的完好柱殼都是失效在彈性區間或者是彈塑性區間。在中部腐蝕減薄的3 種試件RC，SC，OC 中，中部長方形減薄柱殼OC 的臨界載荷值則明顯小于其他2 種柱殼，最大差值達到14.53 kN，其差異程度約為其承載能力的16.7%，這表明腐蝕形狀對柱殼的承載能力有非常大的影響，其還可能與周向方向的缺陷尺寸成正相關，有待進一步研究。中部圓形減薄柱殼OC 和中部方形減薄柱殼SC 的承載能力相差不大可能是由于其形狀相似。對于缺陷位置不同的柱殼RC 和RE 而言，RC 的最大載荷都要小于RE 的最小載荷，載荷最大差值為2.57 kN，約為其承載能力的2.6%，顯然，缺陷位置對柱殼的承載能力是有影響的。

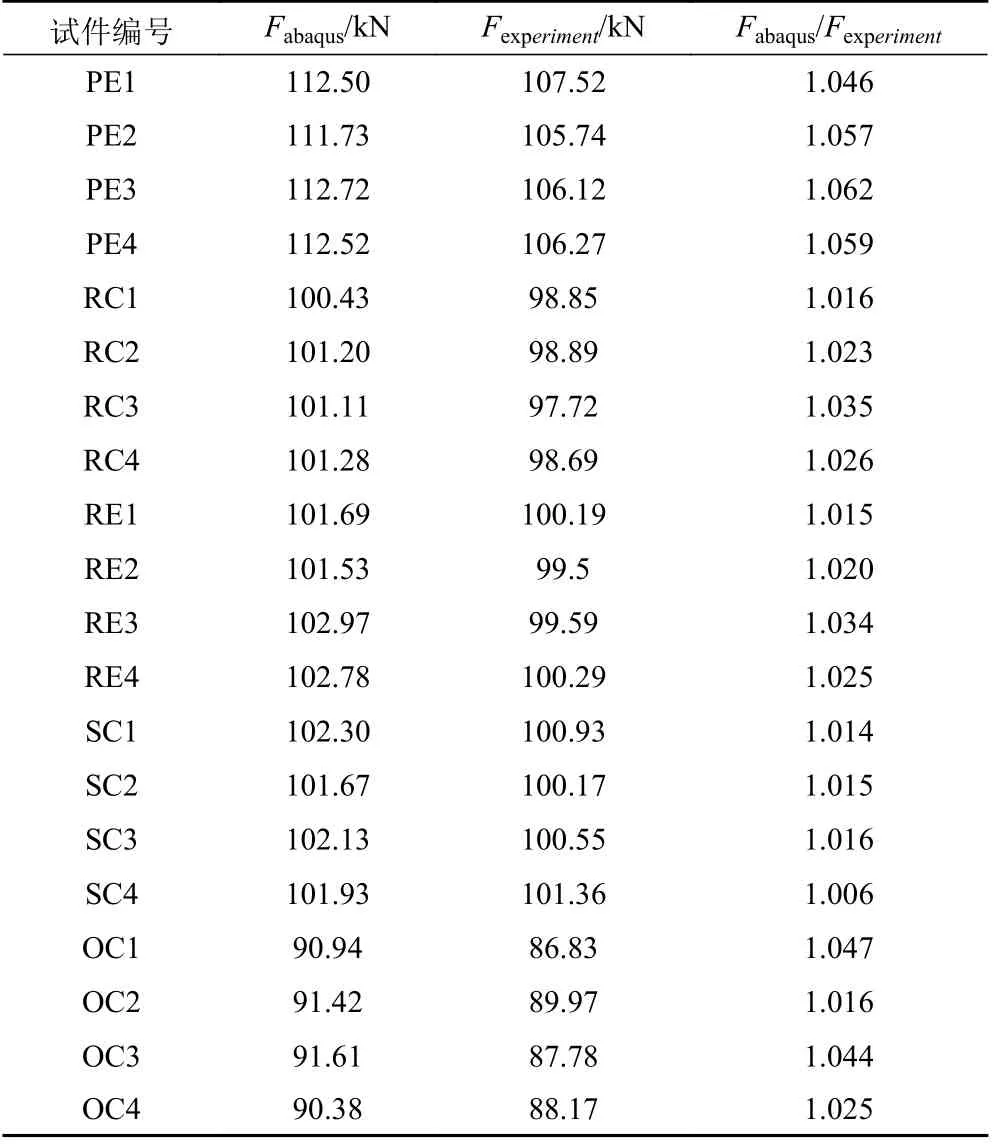
表2 數值計算與試驗極限載荷值Tab.2 Numerical calculation and test limit load value

局部減薄缺陷柱形殼的后屈曲模式如圖5 所示，可知，各組模型的試驗結果具有良好重復性。完好柱殼PE 的4 個試件中1 號，2 號和4 號試件上端發生鼓曲，3 號試件下端發生鼓曲，這表明鼓曲位置的發生不是固定的。可能與柱殼存在的初始缺陷有關。腐蝕柱殼的后屈曲一般呈現為腐蝕區域的凹陷，腐蝕區域上下相鄰區域的凸起。

圖5 柱形殼后屈曲模式Fig.5 Post-buckling mode of cylindrical shells

2.3 數值結果分析

非線性屈曲分析中獲得柱殼的平衡路徑曲線和后屈曲模式，分別將曲線、屈曲模式與試驗所得結果進行對比，以完好柱殼PE2 和腐蝕柱殼中的RC1 為例，如圖6 所示。

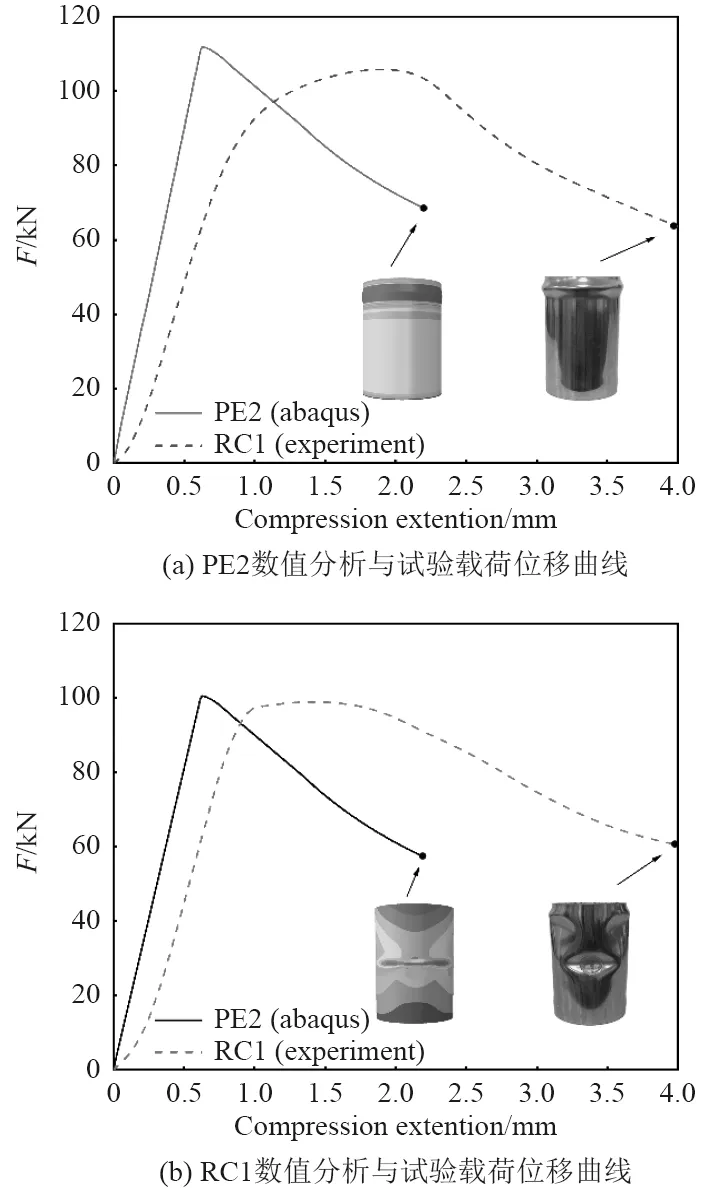
圖6 數值分析與試驗載荷位移曲線比較Fig.6 Load-displacement curves for experimental and numerical analysis

由圖6 可以直觀看出，兩者初始階段的斜率存在偏差。圖中數值計算 所得上升段幾乎為直線,試驗曲線上升階段斜率先逐漸增大之后緩慢減小，減小到0 時即出現臨界載荷。上升階段試驗曲線的綜合斜率要小于數值分析曲線，這會使出現極限載荷的位移值有比較大的偏差。Ifayefunmi[14]認為這種位移偏差可以通過邊界條件改變。圖中有限元與試驗柱殼的后屈曲模式，兩者之間都有很好的印證。完好柱殼的破壞應力和變形主要集中在上端部，對于減薄柱殼而言，不僅上端部同樣存在著較大的破壞應力與變形，其減薄處的變形量更大。

5 種柱殼非線性分析臨界載荷值見表2，與試驗值相近，且重復性良好，其中完好柱殼相差最大，但其中最大的差值也僅有6.2%，證明有限元模型建立的正確性。其次非線性分析減薄柱殼的臨界載荷的誤差是小于完好柱殼的，表明有限元在分析軸壓局部減薄柱殼的問題上也是有效的。

3 結 語

本文進行5 種柱形殼的軸向壓力測試，測試結果具有良好重復性，并進行了殼體的數值計算，數值結果與試驗結果吻合良好，結論如下：

1）柱形殼對腐蝕減薄形狀和腐蝕減薄位置都具有敏感性。尤其對于柱殼周向長方形缺陷形狀的敏感性更強，而對于缺陷位置的敏感則稍弱。

2）完好柱殼的應力應變主要分布在柱殼兩端，失效在彈性或者彈塑性區間，而減薄柱殼的最大應力應變主要存在于減薄缺陷附近。

3）存在減薄柱殼臨界載荷遠小于完好柱殼的情況，表明腐蝕是樁腿承載能力下降的重要原因，柱殼對腐蝕具有較強的敏感性的。

4）有限元分析結果與試驗結果具有較好的重復性，平均誤差僅為3%，這表明有限元在分析軸壓局部減薄柱殼問題上的有效性。