中學(xué)信息技術(shù)課程中滲透算法思想的二進(jìn)制教學(xué)實踐研究

文 / 北京市第八十中學(xué) 賈志勇 中國科學(xué)院附屬實驗學(xué)校 王娟

一、人工智能背景下中學(xué)信息技術(shù)教學(xué)現(xiàn)狀

自2017年7月我國發(fā)布《新一代人工智能發(fā)展規(guī)劃》[1]，提出要在中小學(xué)階段設(shè)置人工智能相關(guān)課程并逐步推廣編程教育以來，以程序設(shè)計課為代表的編程教育在中小學(xué)信息技術(shù)教學(xué)中如火如荼地開展起來[2]。2017年出版的《普通高中信息技術(shù)課程標(biāo)準(zhǔn)》將“算法與程序?qū)崿F(xiàn)”作為必修《數(shù)據(jù)與計算》模塊的一個專題，根據(jù)調(diào)研，編程教育在2013年已進(jìn)入校內(nèi)信息技術(shù)課堂中[3]。

筆者調(diào)研發(fā)現(xiàn)，目前中小學(xué)編程教學(xué)重點往往落在編程語言學(xué)習(xí)上，教學(xué)內(nèi)容圍繞程序設(shè)計的三大結(jié)構(gòu)展開[4]。算法模塊的教學(xué)重點落在解析、枚舉等簡單算法上。隨著新課標(biāo)發(fā)布實施，中學(xué)信息技術(shù)教學(xué)開始以信息技術(shù)核心素養(yǎng)發(fā)展為主要目標(biāo)。針對計算思維核心素養(yǎng)的培養(yǎng)，教師普遍采用項目式教學(xué)策略，引領(lǐng)學(xué)生在完成項目過程中經(jīng)歷 “界定問題—抽象特征—建立結(jié)構(gòu)模型—設(shè)計算法—解決問題—遷移應(yīng)用”的過程，以此發(fā)展學(xué)生的計算思維素養(yǎng)。

二、信息技術(shù)課程中編程教育的核心

中學(xué)信息技術(shù)作為一門以培養(yǎng)學(xué)生信息意識、計算思維、數(shù)字化學(xué)習(xí)與創(chuàng)新和信息社會責(zé)任為要務(wù)的學(xué)科，需要教師深抓學(xué)科本質(zhì)，在日常教學(xué)中彰顯信息技術(shù)課程的思維價值[5]。新課程實施以來，編程教育在中學(xué)信息技術(shù)教學(xué)中占據(jù)一大部分課時，編程教育的核心在于培養(yǎng)學(xué)生以算法思想為主的計算思維能力[6]。本質(zhì)是讓學(xué)生通過設(shè)計程序解決問題來培養(yǎng)算法思想。如何在簡單的編程過程中發(fā)現(xiàn)不一樣的解題思路，拓展視野，逐步培養(yǎng)算法思想，是中學(xué)信息技術(shù)編程教育中需要探索和突破的。

三、滲透算法思想的二進(jìn)制教學(xué)案例分析

算法是解決問題的過程和方法。培養(yǎng)學(xué)生的算法思想，本質(zhì)上也是培養(yǎng)學(xué)生解決問題的思維方法。因此，算法教學(xué)也要基于問題或情景任務(wù)，通過分析問題、設(shè)計算法、解決問題等環(huán)節(jié)，幫助學(xué)生形成解決某幾類問題的方法。

本文根據(jù)中學(xué)生的知識結(jié)構(gòu)，以基本二進(jìn)制為基礎(chǔ)，由二進(jìn)制的概念、二進(jìn)制與十進(jìn)制的轉(zhuǎn)換到以二進(jìn)制為思想的倍增算法，多角度、多切面探討如何設(shè)計任務(wù)和活動環(huán)節(jié)，幫助學(xué)生拓展視野，形成和發(fā)展計算思維。

（一）二進(jìn)制概念教學(xué)

二進(jìn)制概念對學(xué)生來講比較陌生，在進(jìn)行概念教學(xué)時，教師可從學(xué)生熟悉的十進(jìn)制入手進(jìn)行類比法教學(xué)。從十進(jìn)制是由0～9共10個數(shù)字組成的，引出二進(jìn)制是由0～1兩個數(shù)字組成。十進(jìn)制計數(shù)中，從0開始計，當(dāng)計到9時，已經(jīng)沒有數(shù)字可以使用了，因此在9的基礎(chǔ)上向前計數(shù)，需要在前面進(jìn)一位，變成10，這就是十進(jìn)制中逢十進(jìn)一。同樣，二進(jìn)制計數(shù)中，0、1再向前計，沒有數(shù)字可用了，也要前進(jìn)1位，變成10，這就是二進(jìn)制中逢二進(jìn)一的思想。教師可借助圖1示意圖引導(dǎo)學(xué)生理解二進(jìn)制的概念。

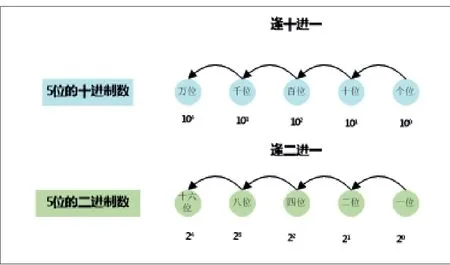
圖1十進(jìn)制與二進(jìn)制概念類比

由類比概念教學(xué)，學(xué)生會理解二進(jìn)制是逢二進(jìn)位的進(jìn)制數(shù)數(shù)碼有0和1兩個，從右向左位數(shù)的權(quán)值為2的對應(yīng)次冪。由少到多，自然理解了多位二進(jìn)制的計數(shù)原理。

此時學(xué)生雖然能理解二進(jìn)制的概念，但對其與十進(jìn)制的關(guān)系還不太容易理解，且類比方法相對抽象，學(xué)生思維容易被分散，可借助游戲方法幫助學(xué)生進(jìn)一步理解其與十進(jìn)制的關(guān)系。

（二）二進(jìn)制與十進(jìn)制的轉(zhuǎn)換

從原理上講二進(jìn)制與十進(jìn)制之間的轉(zhuǎn)換不容易吸引學(xué)生專注力，可借助“猜生日”的游戲方式，吸引學(xué)生興趣。教師可提前制作如圖2所示的生日卡片，找一組學(xué)生說出自己的出生月份和年份分別出現(xiàn)在哪幾張卡片中，教師根據(jù)學(xué)生的回答立即給出學(xué)生的出生月和日。例如，當(dāng)某位學(xué)生說他的月份出現(xiàn)在1、4卡片中，出生日出現(xiàn)在2、3、5卡片中時，教師能立即給出該學(xué)生的出生月日是9月22日。

圖2 生日卡片

教師能在不觀察卡片中數(shù)字的前提下迅速說出月份和日，很大程度上激發(fā)了學(xué)生的好奇心，調(diào)動了后續(xù)知識學(xué)習(xí)的積極性。接下來，從分析問題、歸納抽象、建立結(jié)構(gòu)模型的角度引導(dǎo)學(xué)生解謎老師的神奇之法。

分析問題，已知有5張編了序號的卡片，每張卡片上有16個數(shù)字，問題是出生月日均出現(xiàn)在第幾張卡片上，引導(dǎo)學(xué)生為5張卡片建立如圖3所示的抽象模型，模型是5位的二進(jìn)制數(shù)，二進(jìn)制位編號從右向左編號分別為0、1、2、3、4，若月份出現(xiàn)在第1張卡片中，則第0位為1，否則該位為0。

圖3 生日卡片5位二進(jìn)制數(shù)抽象模型

對于上述學(xué)生的回答月份出現(xiàn)在第1、4卡片中，出生日出現(xiàn)在第2、3、5卡片中，則對應(yīng)月日模型的取值如圖4所示。

圖4 9月22日出生的同學(xué)生日卡片的模型取值

在已經(jīng)理解二進(jìn)制概念的基礎(chǔ)上，教師稍加點撥，學(xué)生即可明白9來自于2的0次冪加上2的3次冪的和，22來自于2的1次冪加上2的2次冪，再加上2的4次冪的和。引導(dǎo)學(xué)生經(jīng)過多次嘗試和練習(xí)后，即可明白二進(jìn)制轉(zhuǎn)十進(jìn)制的方法。

此時，好奇心強(qiáng)的學(xué)生可能會問，生日卡片為什么這樣編排，有何原理？教師可適時引入十進(jìn)制轉(zhuǎn)二進(jìn)制知識的學(xué)習(xí)。十進(jìn)制轉(zhuǎn)二進(jìn)制方法很多，在此例子的基礎(chǔ)上可以利用“除2取余，逆序排列”的方法講解：用十進(jìn)制數(shù)除以2，得到商和余數(shù)；用上一次除法操作得到的商繼續(xù)除以2，又會得到新的商和余數(shù)。反復(fù)執(zhí)行該過程，直到商為零；將上述過程產(chǎn)生的余數(shù)逆序排列即為該十進(jìn)制數(shù)對應(yīng)的二進(jìn)制數(shù)。

在掌握十進(jìn)制轉(zhuǎn)換為二進(jìn)制的方法后，教師引導(dǎo)學(xué)生挑選出卡片上的某幾個數(shù)字，將其轉(zhuǎn)為二進(jìn)制觀察，比如十進(jìn)制31，其對應(yīng)的二進(jìn)制數(shù)為11111，各二進(jìn)制位均為1，因此在第5、4、3、2、1張卡片中均有31；再比如十進(jìn)制21，其對應(yīng)的二進(jìn)制數(shù)為10101，因此在第5、3、1張卡片中均有21。

對于十進(jìn)制轉(zhuǎn)二進(jìn)制，教師可以在學(xué)生理解算法思想的基礎(chǔ)上，引導(dǎo)其用程序?qū)崿F(xiàn)，加深對算法的理解。

（三）巧用二進(jìn)制培養(yǎng)學(xué)生倍增的算法思想

教師可以在學(xué)生掌握二進(jìn)制的概念及基本原理后，增加思維深度，以二進(jìn)制思想為基礎(chǔ)講授倍增算法。

首先讓學(xué)生體驗一個感性和理性選擇游戲：

一份工作，假如有兩種薪資：A方案一個月（按照30天標(biāo)準(zhǔn)）一次性發(fā)放薪資30萬元，相當(dāng)于每天薪資1萬元；B方案按天發(fā)放，第一天一分錢，后一天是前一天的 2 倍，以此類推共發(fā)放30天。讓每個學(xué)生選擇一種方式，引導(dǎo)學(xué)生寫出表1所示B方案每天變化過程，解謎到底哪一種方案更有吸引力。

在寫表1的過程中會發(fā)現(xiàn)，第25天的時候，得到的總薪資已經(jīng)超過30萬，之后每一天都是前一天的2倍，第30天累計達(dá)到了10737418.23元。此時，學(xué)生能夠初步體驗出倍增思想，接下來教師再多切面引出倍增算法應(yīng)用，引導(dǎo)學(xué)生進(jìn)一步體會并理解以二進(jìn)制為基礎(chǔ)的倍增算法思想。

表1 B方案每天薪資變化過程

在Python語言入門階段，學(xué)生學(xué)習(xí)了乘方運算符，計算An可以寫成A★★n的形式。在循環(huán)結(jié)構(gòu)教學(xué)中，教師還會用冪次方的案例講授，例如，“求2的1000次方”，一般的方法是用以下程序片段實現(xiàn)：

這樣程序的效率會比較低，可以用倍增思想優(yōu)化程序。倍增思想的數(shù)學(xué)基礎(chǔ)是指數(shù)冪，從邏輯的角度出發(fā)就是根據(jù)已經(jīng)得到的信息，將下一次的信息擴(kuò)大一倍，從而加快操作。1個字節(jié)的二進(jìn)制數(shù)從右到左，各位的權(quán)值分別為20、21、22、23、24、25、26、27，后一位數(shù)是前一位的2倍數(shù)，可以利用此性質(zhì)快速計算冪次方。

假如求一個正整數(shù)A的128次冪，可以計算1次冪，得到A1,倍增一次就是A★A：A1★ A1=A1+1=A2，再倍增一次，就是讓A2自乘：A2★ A2=A2+2=A4，依此基礎(chǔ)進(jìn)行倍增，會得到A8、A16、A32、A64、A128，做7次乘法計算即可得到A128。

在此基礎(chǔ)上，教師可引導(dǎo)學(xué)生思考如何用倍增思想計算正整數(shù)A的任意次冪。比如要計算A100，可以將冪數(shù)100轉(zhuǎn)化為2的次冪數(shù)，用1，2，4，8，……，2n某幾個數(shù)相加獲得。因為(100)10=(1100100)2，所以100=22+25+26，那A100= A4★A32★A64，假設(shè)A=3，倍增的方法求3100的過程如表2所示。

表2 倍增法求3100的過程

算法核心技巧：根據(jù)b次方轉(zhuǎn)換二進(jìn)制的位數(shù)，有幾位就倍增幾次，答案需要將b的二進(jìn)制位1的位置對應(yīng)的倍增數(shù)累乘，比如364★332★34=364+32+4=3100。顯然，將表2中二進(jìn)制位為1的結(jié)果相乘即可得到3100。

總結(jié)一下，對于A的任意b次冪，倍增法求解的關(guān)鍵在于，將冪數(shù)b轉(zhuǎn)換為二進(jìn)制數(shù)，依據(jù)二進(jìn)制位數(shù)，以A1為基礎(chǔ)數(shù)進(jìn)行倍增，然后將b的二進(jìn)制數(shù)位為1的倍增結(jié)果累乘，即可得到Ab。

用Python語言實現(xiàn)快速冪方法求ab的參考代碼如下：

四、結(jié)語

本文展示和分析了如何在信息技術(shù)教學(xué)中從學(xué)生的興趣點和知識基礎(chǔ)出發(fā)設(shè)計算法教學(xué)案例，在教學(xué)實踐中就某一類問題設(shè)計進(jìn)階式的環(huán)節(jié)幫助學(xué)生逐步掌握解決問題的算法思想，逐步發(fā)展學(xué)生的算法思維。

人工智能新技術(shù)的發(fā)展，給中學(xué)生的生活環(huán)境正帶來日新月異的變化。未來世界，單一技能型人才將不能滿足發(fā)展需要，社會需要更多具有完善知識結(jié)構(gòu)、高階思維能力和強(qiáng)感知力的復(fù)合型人才。

中學(xué)信息技術(shù)作為一門以培養(yǎng)學(xué)生信息意識、計算思維、數(shù)字化學(xué)習(xí)與創(chuàng)新和信息社會責(zé)任為要務(wù)的學(xué)科，需要教師在科技發(fā)展浪潮中深抓學(xué)科本質(zhì)，在日常教學(xué)中貫穿知識與技能，以思維素養(yǎng)為主線，通過知識點間的連接設(shè)計進(jìn)階式的算法教學(xué)內(nèi)容，發(fā)展學(xué)生的計算思維。相信通過這樣長期的實踐，學(xué)生必定會在思維訓(xùn)練和解決問題的實踐過程中成長、成才，未來能夠運用學(xué)到的算法思想，探索真實的世界，解決真正的問題。