面向多用戶NOMA-IRS系統的公平性優化

韓永康,陳 健,周雨晨,楊 龍

(西安電子科技大學 通信工程學院,陜西 西安 710071)

1 引 言

隨著移動互聯網業務的井噴式發展,對高系統容量的無線接入技術的需求與日俱增。然而,面對日益緊張的頻譜資源,傳統的正交多址接入(Orthogonal Multiple Access,OMA)技術難以承載激增的移動通信業務。為提升頻譜利用率及系統容量,非正交多址接入(Non-Orthogonal Multiple Access,NOMA)技術受到了廣泛關注[1-2]。相比于傳統OMA技術,NOMA在相同“時-頻-碼”域資源上,以不同功率疊加多路用戶信號,通過接收端的連續干擾消除解碼多用戶信息流,進而實現功率域多址接入[3]。另一方面,作為一種新型無線物理層技術,智能反射面(Intelligent Reflection Surface,IRS)通過控制各反射單元對信號的移相,實現信號的反射波束成形,在增強用戶期望信號的同時,抑制用戶非期望信號的接收強度[4-8]。因此,將IRS技術與NOMA技術融合,構建NOMA-IRS系統,將有望在提升頻譜利用率的同時,改善用戶接收信號質量。

現有關于NOMA-IRS系統的研究可分為:兩用戶NOMA-IRS系統[9-10]和多用戶NOMA-IRS系統[11-12]。針對兩用戶NOMA-IRS系統,ZHU等[9]通過聯合優化基站端數字波束成形與IRS端反射波束成形,實現了發送功率的最小化。其考慮兩用戶信道方向對齊的理想準退化條件,以保證NOMA能夠達到與臟紙編碼相近的高容量域,實現了良好的速率-功率折衷。此外,FANG等[10]針對兩用戶NOMA-IRS系統提出了一種基于連續凸逼近及半定松弛(Semi-Definite Relaxation,SDR)的迭代優化算法,通過在每次迭代中交替優化基站端發射波束成形與IRS端反射波束成形,逐步提升系統總速率與總功率間比值,實現了能量效率的最大化。另一方面,針對多用戶NOMA-IRS系統,ZENG等[11]考慮NOMA-IRS上行傳輸,通過聯合優化用戶端發射功率與IRS端反射波束成形,實現了系統容量的最大化。其將NOMA-IRS與OMA-IRS系統進行比較,證明了NOMA-IRS系統容量隨用戶數量呈對數形式增長,且性能優于OMA-IRS系統。MU等[12]將多用戶NOMA-IRS系統分為振幅、相位皆連續可調的理想IRS系統與振幅固定、相位可調的非理想IRS系統。針對理想IRS系統,其提出了一種基于連續凸逼近的迭代優化算法,通過在每次迭代中交替優化基站端發射波束與IRS端反射波束,實現系統吞吐量最大化;針對非理想IRS系統,提出了一種基于連續秩1約束松弛算法,通過交替優化基站端發射波束與IRS端反射波束,逐步提升系統吞吐量。綜上所述,現有NOMA-IRS相關研究,大多聚焦于系統吞吐量、能量效率等方面,并沒有進一步考慮系統用戶公平性問題。然而,在實際通信場景中,信道質量差的用戶也有迫切的通信任務需求,因此,在優化系統吞吐量等整體性能的同時,也應關注于個體用戶傳輸信噪比等通信指標,以保證每個用戶都可以較為公平地享受優質的通信服務,這是現有通信系統面臨的一個重大問題。

針對上述問題,建立了多用戶NOMA-IRS系統模型,以最優化用戶間最小信干噪比(Signal to Interference plus Noise Ratio,SINR)為目標,旨在提升系統公平性,無差別保證各用戶的通信質量。為解決由基站端發射波束成形、IRS處反射波束成形、用戶分簇及功率分配多變量耦合而成的非凸分式規劃問題,針對具有代表性的簇頭用戶提出“發射-反射”波束成形聯合優化方案,并采取同簇內用戶復用簇頭波束的方式,提出等效信道相關性的分簇方案,在最大化簇頭用戶最小SINR的同時,保障簇內用戶具備一定性能收益。最后在簇內進行合理的功率分配以保證各用戶的通信質量。仿真分析驗證了提出方案在用戶分簇與波束成形優化方面存在顯著的優勢。

2 系統模型

考慮如圖1所示的多用戶NOMA-IRS下行系統,假設基站配有L根天線和M條射頻鏈路,K個單天線用戶均勻分布在基站的覆蓋范圍內。考慮射頻鏈數受限的一般情況,用戶數大于射頻鏈數(K≥M)[13],并且多個用戶可共用同一條射頻鏈以使用波束成形技術降低用戶間干擾。假設用戶可分簇,且分簇的數量等于射頻鏈數[3],第m(m∈[1,2,…,M])個簇內用戶數量表示為Nm,其中同一簇內用戶采用NOMA方式進行通信。此外,一個配有Q個反射單元的IRS位于基站與用戶之間,輔助用戶通信并抑制簇間干擾。由IRS形成的反射陣元矩陣表示為

圖1 IRS輔助的多用戶NOMA系統

(1)

其中,βq∈[0,1]與θq∈[0,2π)分別表示第q個反射單元施加在入射信號上的振幅與相移,且每個反射單元必須滿足|eq|≤1,1≤q≤Q的振幅約束。

基站到第m簇第n個用戶的信道矢量表示為hd,m,n∈CL×1,基站到IRS的信道矩陣表示為G∈CQ×L, IRS到第m簇第n個用戶的信道矢量表示為hr,m,n∈CQ×1。相應的歸一化波束成形矢量wm∈CL×1滿足|wm|=1。因此,基站端發送信號為

(2)

(3)

(4)

3 問題建模

在實際場景中,為兼顧各用戶服務質量要求,同時保證資源分配的公平性,從整個系統的角度出發,最大限度提高場景中用戶的最低信道容量[14]。考慮最大最小SINR問題,目標是實現用戶間最小信道容量最大化,從而無差別地保證各用戶的通信質量,問題表示為

(5)

其中,C1表示用戶接收到的總功率不能大于基站最大發送功率,C2表示發射波束成形矢量的歸一化約束,C3表示IRS反射陣元的振幅約束,C4表示簇內NOMA的SIC解碼順序約束。

在此問題中,基站端發射波束成形與IRS處反射波束成形聯合構成了最大-最小SINR分式規劃問題。IRS的存在不僅引入了額外的模值約束,還使得反射波束與發射波束在SINR處高度耦合,導致所提出的問題具有非凸性和高度非線性。此外,同簇用戶復用同一波束的行為,導致功率分配也加入到分式規劃問題中,提升了聯合優化的復雜度。為解決上述問題,提出針對簇頭用戶的“發射-反射”波束交替優化方案與等效信道相關性的用戶分簇方案,在提升簇頭用戶最小信干噪比的同時保障簇內用戶獲得一定的波束復用增益,進而將原本復雜的非凸問題分步求解。值得注意的是,交替優化得到的結果通常為次優解,但其優勢在于可以大幅降低優化問題的求解復雜度。筆者構造的優化問題涉及多變量的聯合處理,較為復雜,為提高求解效率,采用交替優化算法。

4 問題求解

4.1 簇間問題

在簇間問題中需要考慮各簇頭用戶的選擇、發射波束與反射陣元聯合優化等問題。

4.1.1 簇頭選擇

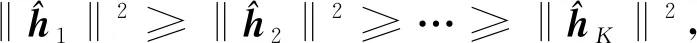
(6)

因此,由簇頭代表的最大-最小SINR問題表示為

(7)

此時該問題仍為非凸問題,需要進一步對發射波束成形矢量與IRS處反射陣元矩陣交替求解。

4.1.2 發射波束成形優化

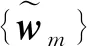
(8)

考慮到約束C1的左右兩端皆存在關于發射波束矢量的二次形式,無法對其直接使用凸優化理論找到最佳波束矢量,采用SDR算法對此問題進行近似求解,將二次項寫成半正定矩陣形式,波束成形矢量和波束空間信道可等價轉換為

(9)

基于式(9)轉化后的約束C1具有xy≤z的結構,其中x、y、z均為非負變量。因此,能夠應用AGM不等式[16]得到這個非凸約束的安全逼近。在引入SDR方法放寬秩1約束后,原問題在多項式時間內可解,此時發射波束成形優化問題表示為

(10)

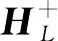
4.1.3 反射波束成形優化

取得發射波束成形跟蹤矩陣Wm后,優化反射陣元矩陣E。相似地,將式(7)中復雜的目標函數,通過輔助變量tm來簡化,問題可以等價地轉化為

(11)

該問題與發射波束成形優化問題略有不同,其中約束C2由IRS的無源特性產生,主要針對IRS每個陣元上的振幅進行約束。與基站端發射波束成形優化類似,此時約束C1仍具有xy≤z的結構,同樣應用AGM不等式得到這個非凸約束的安全逼近。另一方面,針對約束C4引入SDR方法放松秩1約束,使其在多項式時間內可解,進一步轉化成如下凸問題:

(12)

算法1發射-反射波束成形交替優化算法。

① 初始化:隨機反射波束成形矢量E(0),并且設置當前迭代數n=0;

② 循環;

③n=n+1;

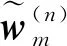
4.2 簇內問題

本節主要研究簇內問題中,用戶分簇與簇內功率分配的解決。

4.2.1 用戶分簇

在海量用戶場景中射頻鏈路數量往往受限,導致無法為每位用戶設計一條適合其信道狀態的發射波束。文中基于分簇思想,將大量用戶分為少數用戶簇,在同簇內復用同一波束,能夠在減小簇間干擾的同時,有效地提升通信鏈路質量。已知由于信道的空間方向性,信道高度相關的用戶應分配到同一簇內以充分利用波束復用增益,而信道不相關的用戶應分配到不同的簇中以減少干擾[12]。由此提出一種基于等效信道相關性的用戶分簇方案。利用用戶ui與簇頭um ,1等效組合信道矢量之間夾角的余弦來度量信道的相關性:

(13)

對于用戶ui,將其與M個簇頭用戶分別比較相關性,得到如下集合:

(14)

選取式(14)中的最大值,將用戶ui與相關性最大的簇頭用戶um ,1歸入同簇中。

4.2.2 功率分配

(15)

(16)

基于式(16)中簇內各用戶功率表達式,可將式(15)中約束C2、C3進行等價轉化,問題可表示為

(17)

針對此凸問題,利用二分搜索可以找到滿足簇內功率約束下ηm的最優解,從而問題得以解決。

4.2.3 復雜度分析

文中旨在提出面向簇頭用戶的發射-反射波束聯合優化方案,通過同簇內用戶復用簇頭波束增益的方式,在最大化簇頭用戶最小SINR的同時,保障簇內用戶具備一定性能收益。具體地,選取信道增益最大的前M個用戶作為簇頭,針對簇頭用戶完成發射-反射波束交替優化,針對剩余用戶依據用戶信道相關性實現用戶分簇,并從進一步強化用戶信干噪比的角度出發,實現簇內功率的合理分配,從而無差別地保證各用戶的通信質量。

所提方案的復雜度主要在于發射-反射波束成形聯合優化算法1。針對式(10)和式(12)的凸優化問題,可用現成的求解器進行有效的求解,文中使用帶有內部求解器SeDuMi的CVX建模包進行求解[17],其使用內點法求解式(10)和式(12)的復雜度主要由迭代復雜度與每次迭代成本兩部分組成[18]。其中,發射波束優化問題式(10)具有M個3維二階錐(Second-Order Cone,Soc)約束、M個1維線性矩陣不等式約束與M個L維線性矩陣不等式(Linear Matrix Inequality,LMI)約束;反射波束優化問題式(12)具有M個3維SOC約束、(Q+1)個1維SOC與1個(Q+1)維LMI約束。因此,所提方案的總復雜度為

(18)

其中,T表示交替迭代次數。β1=M(L+1)+2M,β2=2M+3(Q+1),決策變量n1=M(L2+1),n2=(Q+1)2+M,ε表示精度閾值。

5 仿真分析

5.1 參數設置與對比方案

為研究所提出策略在多用戶NOMA-IRS系統中的性能,對不同信道參數下用戶最小SINR進行了仿真。基站位于(0 m,0 m),IRS反射單元位于(20 m,7 m),K=4至10位用戶均勻分布在基站覆蓋范圍內。基站端配備有20根發送天線,IRS擁有10個反射陣元,用戶處的噪聲功率:

(19)

此外,還考慮了距離相關的路徑損耗模型[19]:

PL=C0(d/d0)-α

,

(20)

其中,C0=-30 dB表示參考距離d0=1 m的路徑損耗,α表示路徑損耗指數,d表示發送端與接收端之間的距離。基站-用戶、基站-IRS和IRS-用戶的路徑損耗系數分別為3.5、2.5和2.2。考慮基站-用戶、基站-IRS和IRS-用戶的鏈路為萊斯衰落,其表達式如下:

(21)

其中,GLOS表示視距鏈路的確定成分,GNLOS表示視距鏈路的瑞利衰落成分,KR≥0表示萊斯因子。用于高斯隨機化的隨機矢量數目是2×106次,所有結果均為1 000次獨立信道上實現結果的平均值。此外,為體現文中方案的性能優勢,仿真將文中方案與如下4種方案進行對比:

(1) 射頻鏈充足(Adequate RF chains)方案:假設射頻鏈路充足的理想環境,每個用戶自成一簇且擁有一個獨立的波束矢量wk,此時模型被擴展至每個用戶以OMA的形式獨立傳輸。此時,由于用戶單一成簇,因此不存在簇內干擾,但簇間干擾仍需進行考慮。

(2) 窮舉搜索分簇方案:遍歷所有的用戶分簇方案,取用戶最小SINR的最大值輸出。發射波束與反射波束依據算法1進行交替優化。

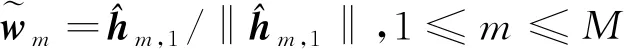
5.2 仿真結果分析

5.2.1 用戶分簇對系統性能的影響

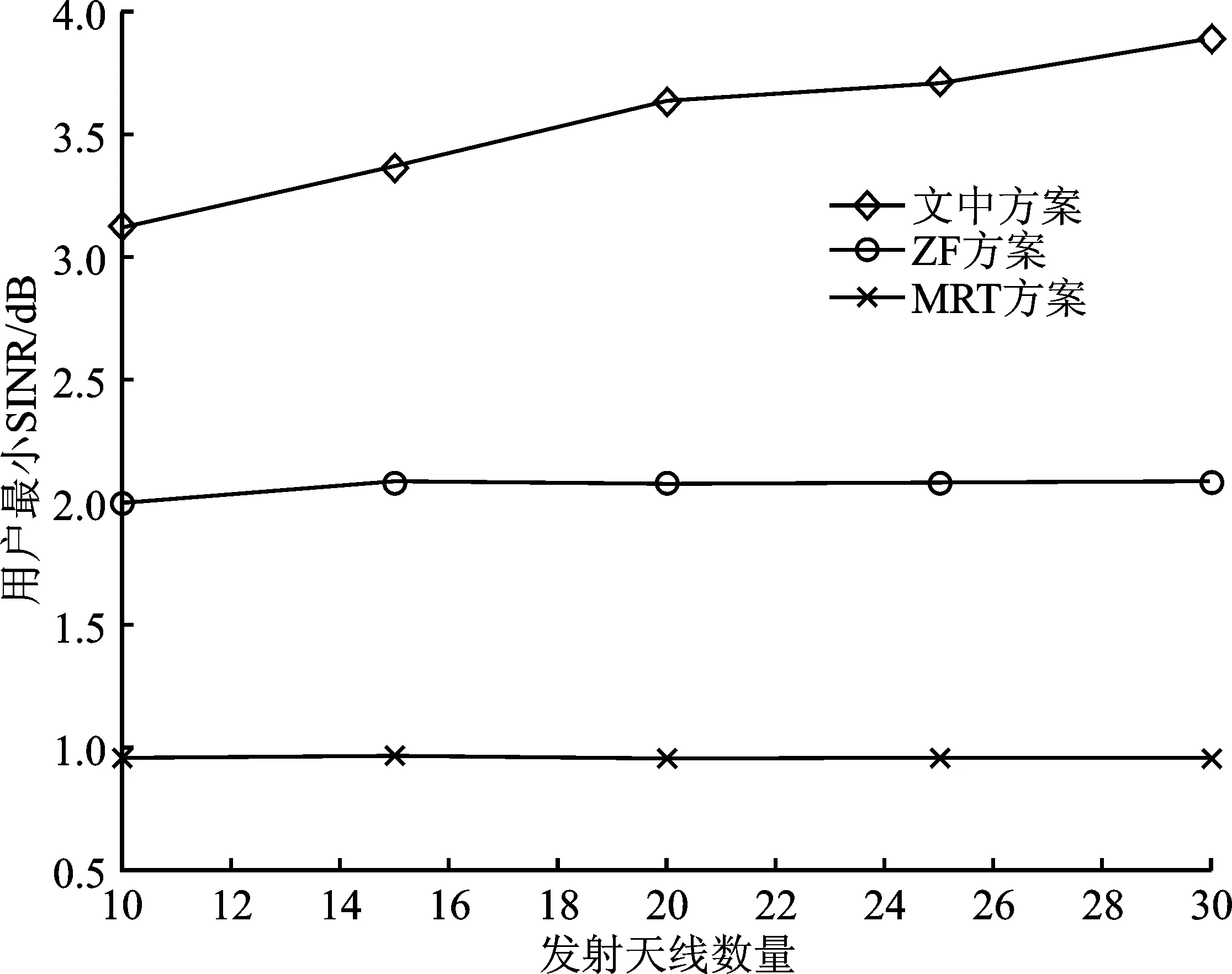
圖2展示了用戶最小SINR隨基站發送功率的變化關系,其中用戶數量K=4,基站端發射天線數量L=20根。由圖可見,隨著基站端發射功率增加,用戶的接收功率也隨之增大,用戶最小SINR的提升帶來了各用戶通信質量的提升。值得注意的是,Adequate RF chains方案取得了最佳效果,這是由于該方案是文中提出方案的上界。在考慮射頻鏈數受限的一般情況(M

圖2 用戶最小SINR隨基站發送功率的變化關系

圖3展示了用戶最小SINR隨簇內用戶數量的變化關系,其中基站端發送功率Pmax=30 dBm,發射天線數量L=20,分簇數量M=2。由圖可見,隨著簇內用戶數量的增加用戶最小SINR顯著下降,其原因在于:①簇內用戶數量的增加導致固定的發送功率被分給了更多用戶,每個用戶分配到的功率降低;②簇內用戶數量的增加導致簇內用戶間干擾提升,因此用戶SINR顯著下降進而導致各用戶通信質量降低。值得注意的是,文中方案與隨機分簇方案隨著簇內用戶數量的增加相互接近,這是由于用戶數量的增加產生了更多獨立信道,在依據等效信道相關性進行用戶分簇時,無法保證同一簇內用戶依然保持較高的信道相關性,進而導致簇內用戶復用波束增益的效果變差以及兩方案的用戶最小SINR顯著下降的同時彼此接近。

圖3 用戶最小SINR隨簇內用戶數量的變化關系

5.2.2 波束成形方案對系統性能的影響

圖4比較了文中方案、MRT方案、ZF方案3種不同波束成形方案的用戶最小SINR隨發送功率的變化關系,其中用戶數量K=8,分簇數量M=2,發射天線數量L=20。由圖可見,隨著基站發送功率的增加,文中方案與ZF方案的最小SINR顯著上升且文中方案優勢逐漸增大,這是由于ZF方案僅關注簇間干擾最小化,而文中方案則以各簇中最小信道容量最大化作為優化目標,有利于用戶最小SINR的提升,從而無差別地提升各用戶的通信質量。此外,MRT方案在低發送功率時優于文中方案,但隨著發送功率的增加,最小SINR逐步趨于穩定。這是由于MRT方案的波束成形固定指向用戶方向,并沒有考慮簇間干擾。在低功率階段,簇間干擾較小,指向簇頭用戶方向更有助于功率的均衡分配。但是在高功率階段,簇間干擾逐步增大,此時不考慮干擾問題會導致發送功率冗余,無法將所有可用功率合理分配,致使MRT方案在高功率范圍收斂。因此,文中波束成形方案綜合考慮了用戶信道條件與簇間干擾,用戶最小SINR隨著基站發送功率的提升逐步增強,從而保證了各用戶通信質量的持續增長。

圖4 用戶最小SINR隨基站發送功率的變化關系

圖5比較了文中方案、MRT方案、ZF方案3種不同波束成形方案得到的用戶最小SINR隨發射天線數量的變化關系,其中用戶數量K=8,分簇數量M=2,基站端發送功率Pmax=40 dBm。由圖可見,隨著發射端天線數量的增加,文中方案的用戶最小SINR逐步提升,而MRT方案和ZF方案的用戶最小SINR趨于飽和,這是由于基站端發射天線數量的增加為波束成形帶來了更高的自由度,然而,由于MRT方案的波束方向固定,ZF方案只考慮了簇間干擾消除,因此二者無法很好地利用天線自由度。但是文中方案以各簇中最小信道容量最大化為目標,利用增加的天線自由度取得了更優的發射端波束成形矢量,無差別地提升了各用戶通信質量。

圖5 用戶最小SINR隨發射天線數量的變化關系

6 結束語

筆者研究了多用戶NOMA-IRS系統公平性問題,嘗試在射頻鏈路受限的實際場景中最大限度提升用戶間最小接收信干噪比,從而無差別地保證各用戶通信質量。為解決發射波束成形矢量、反射波束成形矢量、用戶分簇方案以及用戶間功率分配多變量耦合的非凸分式規劃問題。首先選取了具有代表性的簇頭用戶,并提出了一種基于AGM-SDR算法,對其進行“發射-反射”波束聯合優化,通過在每次迭代中交替優化基站端發射波束成形與IRS端反射波束成形,實現各簇中最小信道容量的最大化。進而,為充分利用波束復用增益,通過同簇用戶共享波束的方式,提出了一種等效信道相關性的用戶分簇方案。最后,以用戶間最小信道容量最大化為目標,使用二分搜索算法解決了用戶間功率分配問題。仿真結果充分論證了所提基于等效信道相關性的分簇思想具有合理性,并且證明了所提出的AGM-SDR波束優化算法顯著優于ZF、MRT算法。