模糊空間下雙標簽指紋定位算法

鄭安琪,秦寧寧

(江南大學 輕工過程先進控制教育部重點實驗室,江蘇 無錫 214122)

1 引 言

全球導航衛星系統(Global Navigation Satellite Systems,GNSS)的不斷成熟,極大地支撐了室外場景豐富的定位應用。但建筑物遮擋導致衛星信號被遮蔽,室外通用的衛星定位技術,顯然無法簡單地移植到復雜的室內定位場景中,尤其在精度、穩定性、時效等性能方面難以得到保證。因此,低誤差、高可靠的室內定位技術成為了定位導航領域的一個研究重點。隨著室內WiFi信源的廣泛部署與智能移動設備的普及應用,以信號強度為導向的指紋定位算法,由于其高成本效益與對環境的普適性特征,已成為最常用的方法之一[1]。該方法在離線階段,完成對各參考點(Reference Point,RP)位置的標記以及對其可見接入點(Access Point,AP)接收信號強度(Received Signal Strength,RSS)的樣本采集和分析處理,構建指紋庫[2]。在在線階段,將待定位點實時接收的RSS向量與離線指紋庫樣本進行匹配,實現目標的空間位置估計。

傳統的指紋定位方法,通常是將待定位點與指紋庫中參考點依次進行相似性匹配,在帶來高計算量的同時也導致定位精度受參考點分布影響較大。為降低計算負擔與提高定位精度,聚類算法被引入指紋定位中。離線階段對指紋數據庫進行簇群化處理,如k-means[3-4]、模糊C均值(FCM)[5]以及仿射傳播聚類(APC)[6]等方法,將整個目標區域劃分為多個子區域,利用簇類切分形式實現在線階段簇群匹配,以待定位點與所屬簇群內參考點的相似度匹配替代全局比對過程。但不同于單純的數據聚類處理,作為數據通道的無線信道,具有不可預測的動態衰減、多徑效應等特征,導致指紋信息難以具有絕對清晰的簇間邊界,簇間過渡區對于邊緣點信息歸屬誤判的影響明顯。

除離線聚類因素外,在線匹配對于定位的有效性,也起著至關重要的作用。加權K近鄰算法(WeightedK-Nearest Neighbor,WKNN)[7]通過計算待定位點與指紋庫中相似度最高的K個近鄰參考點的加權質心實現位置估計,但對于目標移動、障礙物變化、接入點狀態改變等環境特性考慮欠缺;固定的K值和分散的指紋點選取,也將無法避免遺失重要空間信息甚至引入虛假離群點的問題[8]。為適配環境的動態變化,以多目標優化構建準則模型[9],實現對在線接入點的自適應篩選;或者通過參考點排序[10],削弱相似度判斷標準的不穩定,但此類方案均缺乏信號動態差異對定位影響的考慮。為應對參考點固定選取無法適應指紋動態變化的不足,王培重[11]基于動態K值概念,去除歐式相似度小于閾值的指紋點來保證一定的定位精度,但仍無法確保離群點篩除;TAO[12]通過單獨處理來自每個接入點的接收信號強度,強化近鄰點位置的集中,但算法時間復雜度較高,實時性無法得到保證。

為解決簇間邊界模糊、環境和信號動態特性對指紋定位結果的交叉干擾問題,筆者提出了一種模糊空間下雙標簽指紋定位算法(Dual-Label fingerprint localization algorithm in Fuzzy Space,DLFS)。以參考點“類間-類內”的雙距離差異,刻畫待定位場景過渡區域的模糊度,尋求區域判別精度和時間代價之間的平衡;將區域重疊分布上的增益效果,輻射影響到在線待測點位置估計,結合指紋排序弱化參考點匹配誤差,利用指紋信號域和空間域迭代約束近鄰點集合。這種模糊劃分機制可以有效減少定位匹配工作量,在重新定義相似度判斷標準的基礎上,實現最佳近鄰點的自適應選擇,降低了近鄰點空間位置分散和固化近鄰集合對定位結果的不利影響。

2 系統模型

3 離線劃分

3.1 平面空間分類

通過區域劃分,可以有效縮小最佳定位點的尋找范圍。但以指紋點與聚類中心距離作為參考點劃分唯一依據,極有可能導致在線階段待定位點的分區誤判。經典k-means方法通常基于信號域均值相似性,以迭代化方式劃分空間,收斂速度快且聚類效果良好,但對于信號穩定性較差的過渡區域,其參考點最小信號域距離并不一定能映射最小空間域距離,這一沖突在拐角、廊形等復合空間結構中,表現更加明顯。

如圖1(a)中場景采用“一刀切”式非此即彼的硬聚類模式,該方法簡單直接,但很容易使得位于簇間邊界的待定位點TP1存在分類尷尬,甚至導致位于簇Ωs邊緣地帶維穩能力相對較弱的待定位點TP2被錯誤歸屬到近鄰簇Ωt中。與之相比,軟聚類模式則允許樣本同時歸屬于多個原型。綜合考慮樣本點簇間相似性的誤判過程,在原“單一”區域基礎上,對于過渡區域增設具有弱化邊界絕對差異特性的模糊空間Ωs&Ωt,如圖1(b)所示,有條件地擴大匹配范圍,將邊緣待定位點歸屬于模糊空間,有效避免簇間相似度差異不顯著的待定位點的區域誤判現象。

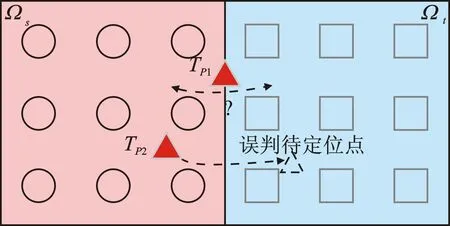
(a) 硬聚類

3.2 雙距離差異軟聚類

3.2.1 雙屬性特征

利用指紋點間的歐式度量,定義聚類形成的簇間距離和簇內距離,以映射各參考點的類間稀疏性和類內緊密性。鑒于樣本點的類間稀疏性與類內緊密性,可在一定程度上反應具有信號域和空間域之間非線性漸變特征的指紋點聚類的有效性[13]。筆者提出以聚類指紋點的雙屬性特征衡量其分類的魯棒性,構建兼具參考點“類間-類內”雙距離差異的軟聚類方法,增加有限的定位計算開銷,彌補嚴格切分時局部匹配算法誤差大的缺陷。

不失一般性,平面空間內的參考點僅以其信號域均值為單一尺度進行初始聚類劃分,生成T個簇Ω1,Ω2,…,ΩT,并記錄其簇中心c1,c2,…,cT。考慮到簇邊緣樣本通常對簇內歸屬度較低,其區域判別更易受信號波動干擾,本文以此建立信號對空間判別影響的更新指標,解決過渡區樣本點簇間相似性的誤判問題。

(1) 類間稀疏度

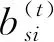
(1)

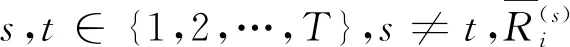
(2) 類內緊密度

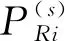
(2)

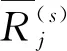
3.2.2 軟聚類生成

(3)

不難發現,f值越大,滿足空間模糊的參考點越多,區域誤判的概率則會越低。

雙距離差異軟聚類算法采用空間重疊分類結構解決基于RSS的指紋點目標區域歸屬問題,在通識的硬聚類算法構建指紋初劃分的基礎上,完成平面空間內所有參考點的雙距離差異對比,判定模糊類屬,進而實現整個目標環境由硬聚類向軟聚類的轉化。

3.3 雙標簽指紋庫構建

平面空間模糊劃分和類別重構過程,保證了每個參考點在離線指紋庫構建中區域歸屬的穩健性。為提升在線定位的時效性,以類標簽(或稱區標簽)和類內點標簽的形式實現離線指紋庫構建。

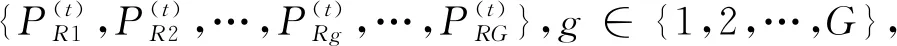
4 在線定位

4.1 區歸屬

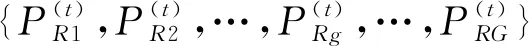
4.2 點排序

考慮到待定位點與參考點位置越接近,則會在更多的接入點下接收到更加相似的信號強度值,將參考點和待定位點之間的RSS差異轉化為相對排序,雖然可以削弱接入點的不確定因素對定位的影響,但信號動態特性所帶來的排序誤差依舊難以避免。基于此,本文不再局限地以點與點間歐氏距離衡量待定位點與指紋點間相似度,而是結合參考點近鄰空間攜帶的定位信息量,弱化信號波動的影響,對參考點進行同源相似度的穩健排序,進而實現與待定位點間多源均衡相似度的有效判斷。

4.2.1 同源相似度

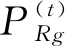
(4)

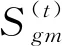
4.2.2 參考點同源排序

場景動態特性及其時間差異使得個別接入點在離線階段和在線階段特征缺乏一致性,甚至會出現絕對差的激增,從而導致待定位點與參考點鄰近程度的誤判。為了保證接入點之間比較的一致性,將同源相似度的量化比較轉化為同源相似度的排序比較,以避免不同接入點間量級差異。參考點同源排序原理定義如下:

4.2.3 野值修正

信號自身波動和同源接入點下的其他參考點排序結果的交叉影響,可能導致部分參考點排序異常,鑒于低維空間域相近的參考點,通常在高維信號域具有更加相似的RSS值[14],因此,同源接入點下的近鄰參考點應具有相近的排序。若某參考點與周圍鄰居點間的同源排序差異較大,該參考點排序為異常值的概率則更高。

在箱線圖[15]過濾異常值方式的啟發下,對同源鄰居樣本升序排序后進行四分位處理,記Qu和Qd為上、下4分位數,4分位距IQR=Qu-Qd,基于Qd和Qu縮放IQR的1.5倍進行有效區間的切分,構建關于歸屬區Ωt內參考點同源排序的野值修正模型:

(5)

4.2.4 參考點多源排序均衡

(6)

需說明的是,均一化后所得非整數排序結果,依然遵循排序規則。

4.3 點匹配

理想狀態下,用于最終位置確定的Ωt個近鄰點應該圍繞待定位點[16],但由于環境的動態干擾和信號自身的波動,傳統KNN、WKNN匹配算法所選擇的Ωt個近鄰點,并不能保證基于待定位點的集聚分布,且固定Ωt值會降低算法對環境的適應能力。為此,提出一種信號域和空間域迭代約束近鄰點集合的定位方法,通過引入空間密度可達判別,搜索強相關參考點集,控制Ωt值自適應,提高近鄰參考點選擇準確性的同時保證其分布的相對集中。

4.3.1 強相關參考點集搜索

以點排序方法獲取歸屬區Ωt中的所有參考點與待定位點的排序結果,取前I(I≤G)個參考點,生成初篩近鄰集P′R={P′R1,P′R2,…,P′Ri,…,P′RI},考慮到信號域的不確定性,會伴隨部分離群點的引入,如圖2(a)所示,為克服野值點迭出對定位結果的不利影響,基于密度聚類[17]思想,利用初篩近鄰點的空間域距離對目標近鄰集進行二次約束。

(1) 以初篩近鄰點P′Ri的空間坐標為中心,ε為半徑,定義P′Ri鄰域為

Eε(P′Ri)={P′Rj∈P′R|d(P′Ri,P′Rj)≤ε} ,

(7)

其中,d(P′Ri,P′Rj)表示集合P′R中兩個初篩近鄰點P′Ri和P′Rj之間的空間域距離,Eε(P′Ri)包含了P′R中與P′Ri空間域距離不大于ε的所有初篩近鄰點。

(2) 設定領域閾值η以反映P′Ri周圍近鄰點密集程度,若|Eε(P′Ri)|≥η,則將P′Ri視為核心點(Core Point,CP)。若存在核心點序列{CP1,CP2,…,CPh,…,CPH}?P′R,2≤H≤I,則依據式(8),判斷序列中相鄰核心點的前置項是否在后置項的鄰域內,并以標簽lh標識:

(8)

形成的H-1個標簽共同決定核心點序列{CP1,CP2,…,CPh,…,CPH}是否具備構成目標近鄰集的可能性,定義

(9)

若L=1,則CPH距離CP1密度可達,表明該核心點序列空間域較為接近,其攜帶的指紋信息相似度較高,具備構成目標近鄰集的可能性;否則,不具備構成條件。

(3) 以任意一個核心點CP作為起點,從該核心點密度可達的所有核心點構成一個簇;再從其余尚未成簇的核心點中尋找可成簇的新起點,以此完成強相關參考點候選集的搜索,如圖2(b)所示,無法成簇的點則被視為弱相關參考點。顯然,領域半徑ε和領域閾值η聯合約束了參考點候選集的相關程度。

4.3.2 目標近鄰集匹配

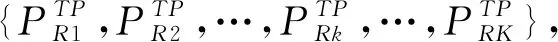
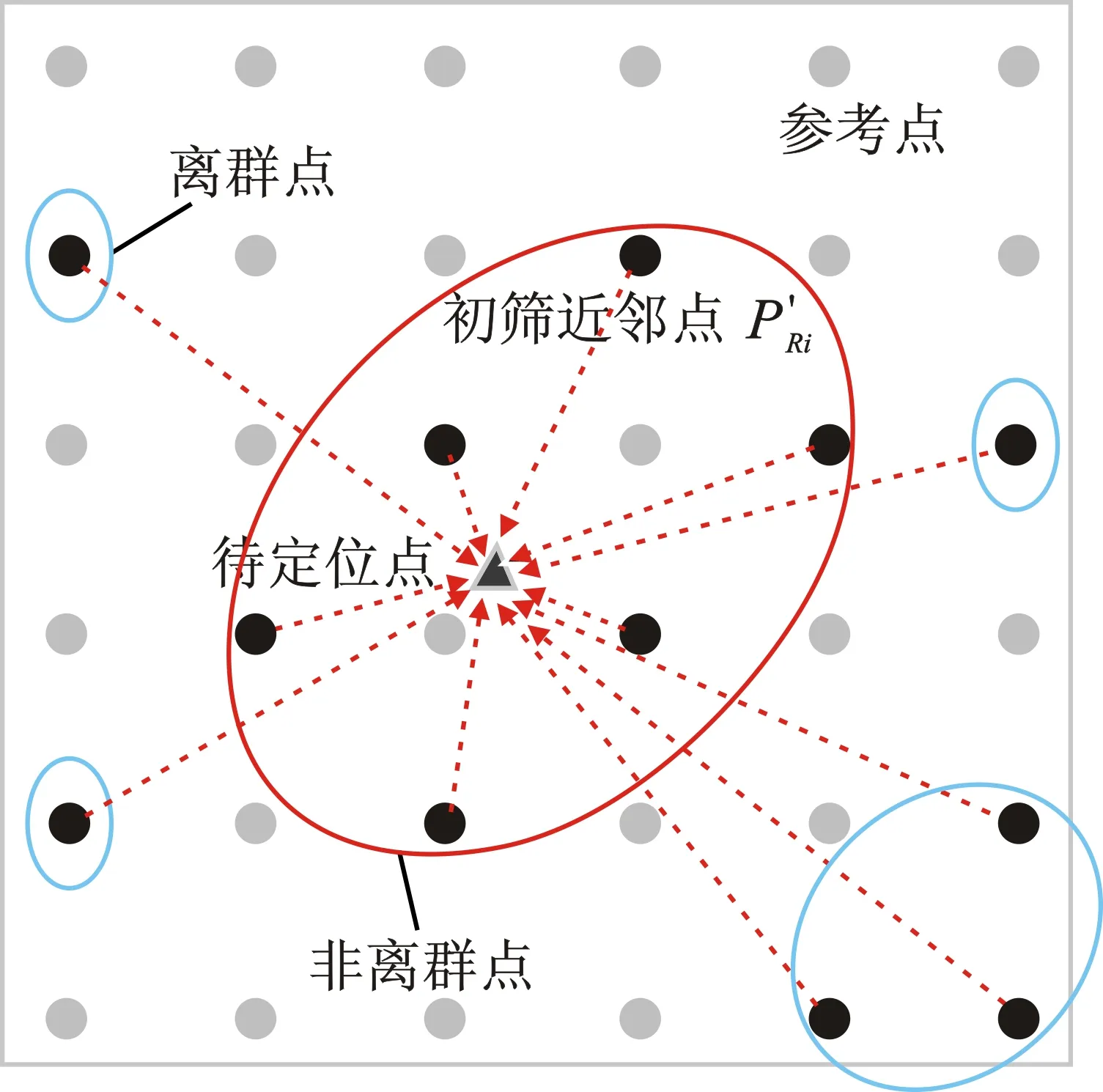
(a)初次約束:初篩近鄰集

需提出的是,存在某待定位點的初篩近鄰集全被判斷為弱相關參考點這一特殊情況,此時則同樣以初篩近鄰集作為該待定位點位置估計的目標近鄰集。

強相關參考點集搜索過程在剔除數據集弱相關參考點的同時,確保了目標近鄰參考點集物理空間位置的集中分布,為待測點TP近鄰點集合的自適應匹配創造了條件,以此克服了因加權質心的偏移而導致定位結果偏差大的問題。

4.4 位置計算

參考點的多源排序均衡結果,體現了參考點和待定位點接收信號相似度的級別,因此以其作為待定位點定位權重的配置基礎,表征如下:

(10)

(11)

5 系統定位流程

文中所提DLFS定位算法的系統流程如圖3所示。針對區邊界待定位點歸屬左右偏移問題,本文基于“類間-類內”指紋信息差異建立“左右逢源”的空間模糊聚類機制;并以構建雙標簽指紋庫的形式,通過類標簽信息提升區歸屬判別效益,引入類內點標簽信息支撐下的參考點排序野值修正以及目標近鄰集迭代約束,以此克服環境和信號的不確定性,使得定位系統更具可靠性。

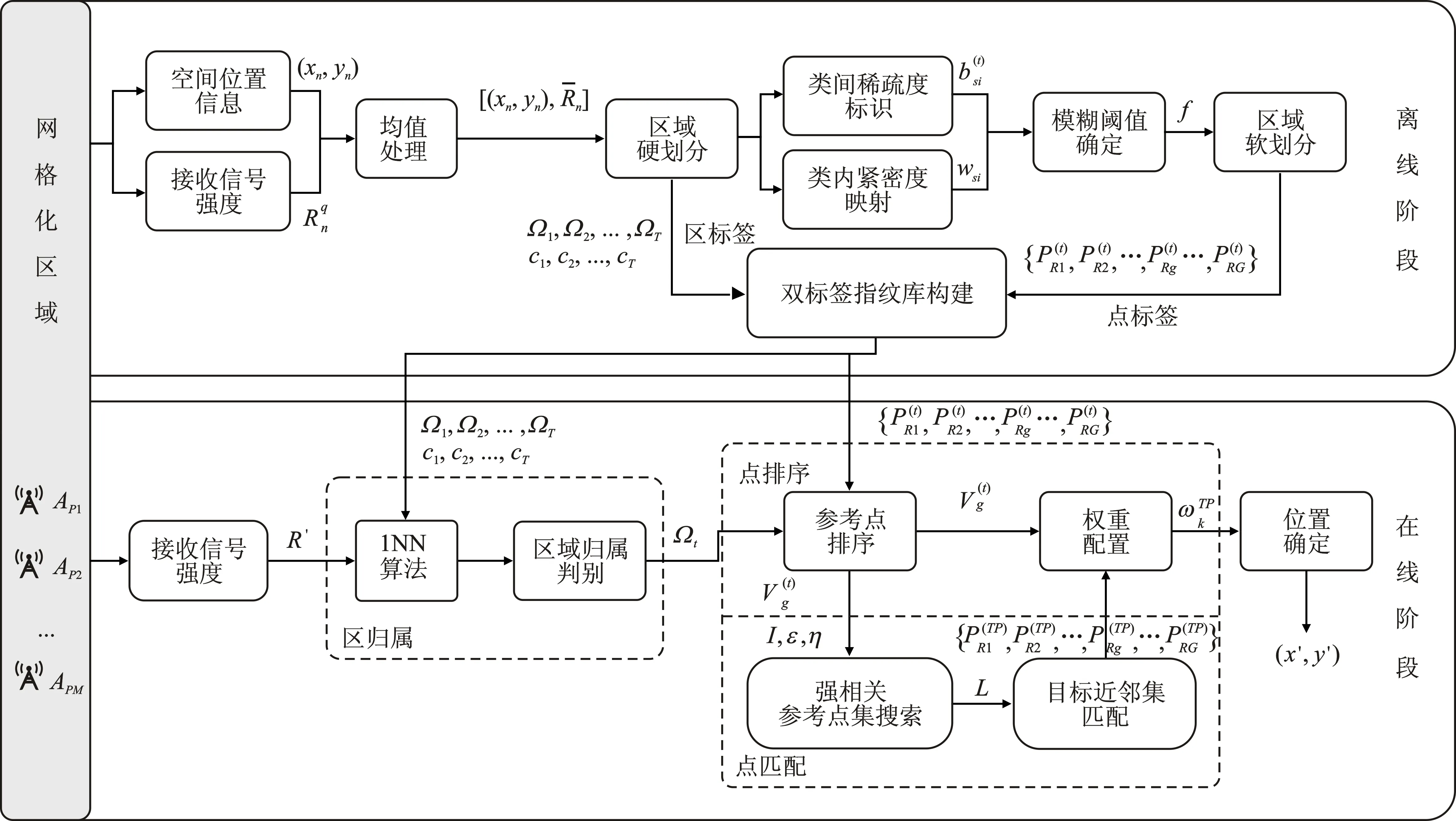
圖3 DLFS定位算法流程圖

6 實驗場景與結果分析

6.1 測試場景與數據處理

為了評估DLFS 定位算法性能,以江南大學物聯網工程學院3樓內,人員走動頻繁的多邊形連通走廊為實景測試場地,該場景可以較好地反映環境多變和信號動態特征對定位的影響,具有很強的實測代表性。

參考點采用均勻網格部署形式,相鄰參考點間隔取1 m,共計N=270個參考點;在全局定位區域共探測到來自M=86個接入點的信號,為保證點與點間計算維度的一致,不失一般性,每個參考點處未探測到的接入點信號強度值以-100 dBm填充[18],并以2.3 s采樣間隔,采集Q=60次指紋數據。沿著實驗走廊中間區域選擇152個在線測試點。為避免設備差異對算法性能評估的影響,離線與在線過程,均使用同一移動終端作為數據采集工具。所有數據均以Matlab 2020a作為處理平臺。

6.2 參數配置對性能的影響

6.2.1 模糊閾值f

模糊閾值f影響著子區域匹配的包容度,f值越大,區域判別精度越高;與此同時,重疊區域的參考點數量將增多,計算代價隨之增大。為兼顧區歸屬正確率和點匹配時效性,以隨機選取離線采集中的60×80%=48次數據取均值作為訓練數據,其余60×20%=12次為測試數據,重復10次試驗,分別記錄區判別正確率和參考點全局增長率的均值,以評估最佳f的配置影響。

實驗對比了不同f值下區判別正確率和參考點全局增長率的變化情況,如圖4所示。可以發現,即使f取值小量程增長,也可顯著提升區判別正確率,且在f=11時,區判別正確率達到99.68%,同時參考點全局增長率僅為10.37%,主要原因在于雙距離差異越小的參考點,越易引發誤判,小范圍的誤差容忍,即可換取系統定位精度的快速上升。此時,若持續擴大f值,區判別精度上升緩慢,參考點的計算量呈現明顯增長。因此,本實驗場景設置模糊閾值f=11。

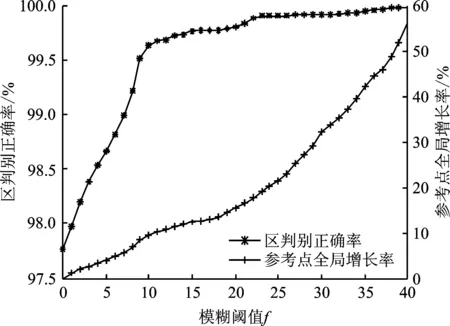
圖4 模糊閾值f對性能的影響

6.2.2 領域參數ε和η

為使系統的定位性能達到最佳,對4.3.1節中的相關參數進行尋優。基于固定近鄰點取值的經驗范圍,綜合考慮強相關參考點集搜索的可行性和計算負擔,折中選取歸屬子區域中參考點總量的20%作為初篩近鄰點的數量,即I=G×20%。為評估定位區域中領域半徑ε∈{1,1.5,2,…,4.5,5}和領域閾值η∈{1,2,…,10}的多重配置方案對定位性能的影響,同6.2.1節中模糊閾值尋優方法一致,以確定各子區域的平均定位誤差最小時的領域參數組合,從而保障待定位點自適應匹配的定位效果。限于篇幅,圖5給出了部分子區域在不同領域參數組合下的定位性能。

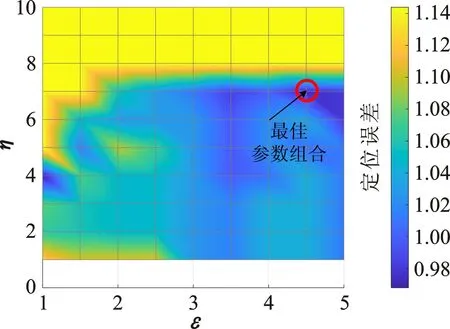
(a) 子區域Ω2

實驗發現,不同的領域參數組合(ε,η),伴隨著子區域不同的定位性能。此外,表1列出了上述子區域在其最優參數組合下,對應子區域內部分待定位點TP在位置計算時的近鄰數K,其匹配差異進一步證明了不同待定位點在定位時目標近鄰集會隨著定位需求發生自適應的改變。

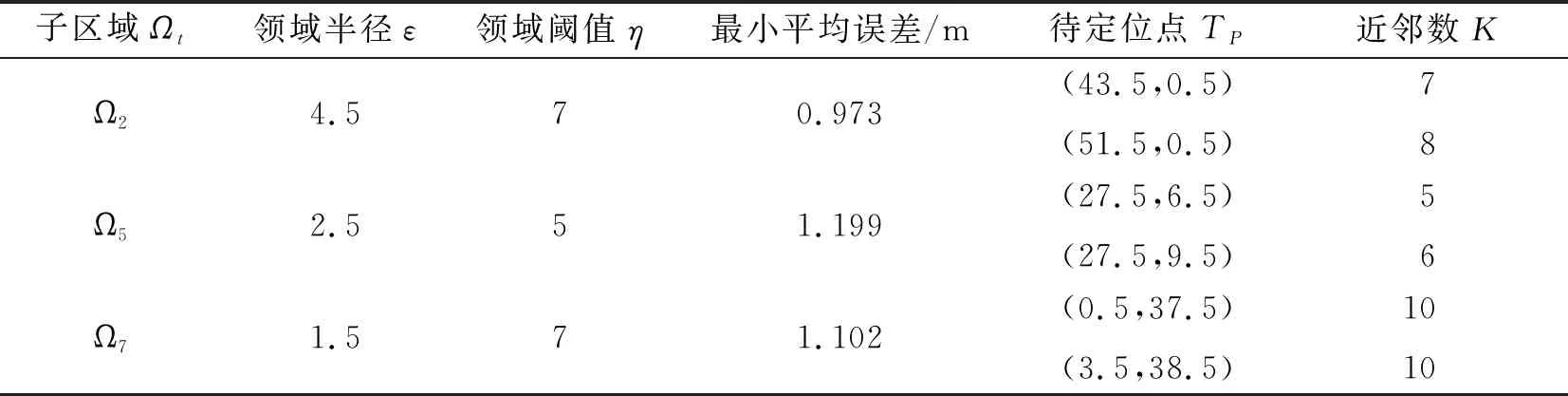
表1 部分子區域內最優領域參數

6.3 區域軟聚類效果分析

考慮到聚類算法的時效性,論文選用常規k-means作為區域初劃分算法,結合環境特性和k-means聚類效益,本實驗場景預設初始聚類數為7。基于模糊聚類機制,配置最佳模糊閾值f=11,形成7個獨立區和6個模糊區,聚類效果如圖6所示。

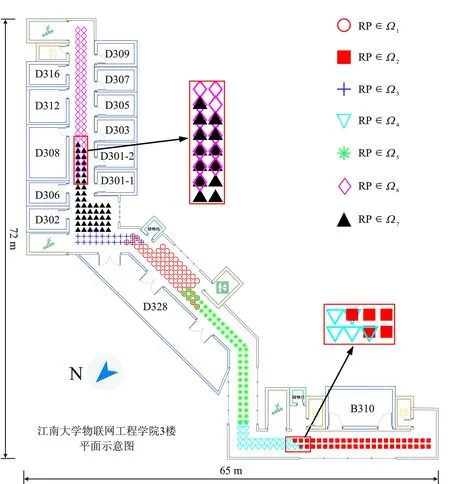
圖6 區域軟聚類結果示意圖

所提算法的軟標記性質體現在雙距離差異較小的28個參考點的重疊劃分上。實驗發現,具有模糊劃分屬性的參考點,基本都位于子區域的邊界處。這些參考點雙區域的歸屬結果進一步印證了過渡區信號穩健性的不足,由于空間結構變化和信號交疊等干擾,使得邊界地帶更易引發區域誤判的問題。顯然,模糊空間的設置,可弱化區域信號不穩定的影響,控制區域定位誤差。

相較于全局式貪婪匹配,本文所提軟聚類方法將整個目標區域內的N=270個參考點降低至局部區域內的24～53個參考點,很大程度上保障了定位的實時性;此外,28個參考點的重疊劃分,分配至各子區域僅相對新增1～7個有限的參考點,對比嚴格的硬劃分算法所增加的局部匹配工作量也是相對可控的。

6.4 在線算法結果分析

針對傳統排序算法對信號動態特性考慮欠缺的問題,本文利用參考點近鄰空間整體信號特征對排序野值進行修正;同時為克服傳統匹配算法K值固定的缺陷,論文基于對參考點信號域和空間域的迭代約束實現K值自適應。為有效評估其對在線定位的價值,論文通過控制算法執行,從“傳統參考點排序+固定K值”“僅執行K值自適應”“僅執行參考點排序修正”“參考點排序修正+K值自適應”4個角度對定位性能進行了對比實驗,結果如表2所示。

表2 在線算法對定位誤差的影響

從實驗數據發現,在參考點排序修正和K值自適應的共同作用下,定位效果最佳,平均定位誤差為 1.138 m,相較于傳統定位的1.327 m提高了18.9%,1 m以內誤差占比提升了9.46%;在線定位中,僅進行參考點排序修正和僅采用K值自適應平均定位誤差分別降低了0.126 m和0.061 m。結果驗證了所提“點排序”和“點匹配”在線算法對定位的可行性和有效性。

6.5 整體定位性能分析

為驗證本文算法DLFS的整體定位性能,分別與6種同類算法進行比較。其中,傳統的WKNN[7]、EWKNN[11]、AAS[10]為3種全局匹配算法;此外,補充3種不同離線區域劃分算法,即APC[6]、FCM[5]、k-means[4],同文中在線方法結合。為了保證對比的公平性,各算法均已選取本實驗場景下的最佳參數進行實驗。

表3總結了不同算法定位性能。實驗結果表明,相較其他方法,本文算法的平均誤差、最小誤差以及方差誤差都是最低的。整體定位場景中,其平均定位誤差為1.138 m,在局部匹配方法中改進了4.7%～11.8%,但最大誤差相差不大;與全局匹配算法相比,本文算法的平均定位誤差至少降低了14.7%。表明本文算法為復雜室內環境下的定位性能帶來了整體性的提升。

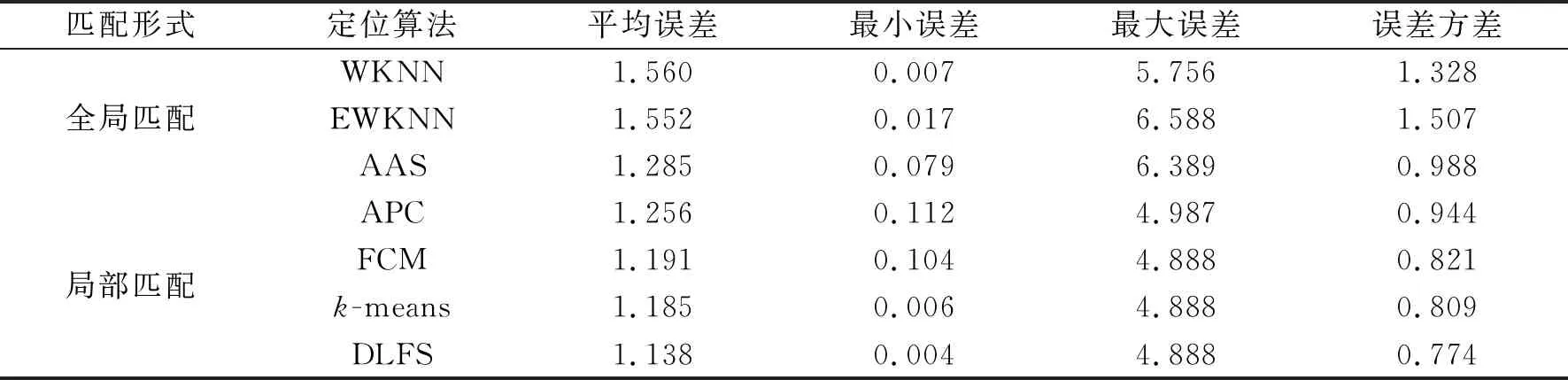
表3 7種定位算法性能比較 m

圖7給出了包含全局匹配和局部匹配在內的共計7種算法的定位誤差累計概率分布,在對待定位點位置估計時,同等精度范圍內,本文所提DLFS算法均優于其他對比算法。DLFS算法在同全局匹配的比較中,有73.78%的估計精度在1.4 m以內,相較于此時的WKNN算法,估計精度提升了21.35%,如圖7(a)所示。由圖7(b)可知,隨著定位誤差范圍的擴大,4種局部匹配方法的誤差累計概率上升狀態趨于一致,當定位誤差范圍擴大至0.4 m后,DLFS算法呈現優勢,并在其擴大至2.4 m時,累計誤差概率達到90.00%。實驗證明,DLFS 在解決環境和信號動態特性帶來的定位問題時具有顯著的優勢,主要得益于該模糊聚類機制在處理邊界信號跳躍問題的敏感性,以及在線定位方法對指紋點與待定位點間相似度的高效衡量。

(a) 與全局匹配算法的比較

7 結束語

針對定位中,匹配效率與定位精度的需求,算法在平衡區域匹配精度與定位計算代價后,構建了待定位場景下的模糊聚類機制。綜合考慮每個參考點的類間稀疏度與類內密集度,實現相鄰區域的簇間邊界調整;借助鄰居指紋信息彌補各參考點波動差異后,采用空間域和信號域迭代約束方案選取各待定位點的最佳鄰近點集合,從而降低定位誤差。實驗證明,本系統模型有效衡量了待定位點與參考點的空間距離,更好地克服了信號和環境的動態影響,在計算量大大減少的同時,在復雜的室內環境中定位效益也較高。