復合干擾影響下戰斗機大機動改進動態面控制*

秦 川 陳 勇 李秋妮 劉棕成 張文倩

1. 空軍工程大學,陜西 西安 710038 2. 中國人民解放軍93793部隊,北京 102100

0 引言

具備大機動能力的戰斗機在現代空戰中可以快速搶占有利位置、先敵開火,同時在遭到敵方武器鎖定時能快速機動擺脫不利態勢,從而顯著提高戰斗機的作戰效能和生存能力[1]。戰斗機在進行大機動飛行時,氣動力和力矩呈現明顯的非線性特性,三軸動力學嚴重耦合[2],同時陣風、紊流等外界擾動也會引起氣動參數變化,導致飛機動力學模型存在較大的不確定性,給飛行控制系統設計帶來巨大挑戰。

反步法(Backstepping)作為非線性系統控制中常用的一種方法,在航空航天領域有著廣泛的應用。文獻[3]針對彈性吸氣式高超聲速飛行器控制問題,在反步法的框架下引入干擾觀測器對復合干擾進行估計補償,設計了一種魯棒控制方案。文獻[4]以反步法為基礎,結合神經網絡設計了高超聲速飛行器的魯棒自適應控制器。文獻[5]將反步法與滑模控制相結合,為衛星姿態控制系統設計了容錯控制器。文獻[6-7]將反步法用于飛機的飛行控制器設計,取得了良好效果。然而,傳統反步法需要對虛擬控制信號進行反復求導,導致控制律過于復雜,產生“微分爆炸”問題[8]。針對反步法的這一固有缺陷,文獻[9]提出了動態面控制方法,通過引入一階低通濾波器得到虛擬控制信號的一階微分近似值,避免了對虛擬控制信號的直接求導,簡化了控制律。動態面控制的核心是利用濾波器得到中間虛擬控制信號的一階微分近似值,因此選擇其他性能更優的濾波器代替一階低通濾波器有助于改進動態面的控制效果。

神經網絡對非線性函數具有良好的逼近能力,常用于處理系統中的不確定性,將動態面和神經網絡結合,許多模型含有不確定性的飛行控制問題就能得到解決[10-14]。然而,用神經網絡逼近未知函數需要清楚未知函數由哪些變量構成,當變量信息不足時,神經網絡無法實現對函數的估計。由于實際飛行系統極其復雜,飛行器在飛行過程中所受干擾不確定,無法精確得知飛行器模型的不確定部分由哪些變量構成,因此神經網絡方法存在一定的局限。此外,將模型不確定性作為復合干擾的一部分,基于干擾觀測器進行控制器設計也是一種有效的方法[15-18]。但是,常規干擾觀測器常需要假設干擾可導甚至慢時變[19-22]。這一假設在實際應用時過于嚴苛,因為實際被控系統很可能會受到死區、齒隙等不可導干擾的影響。而對于戰斗機這樣的對控制性能要求很高的復雜系統,考慮不可導干擾是很有必要的。文獻[23]提出了一種新型干擾觀測器,可有效處理不可導干擾,但是文中設計的干擾觀測器結構復雜,需要調整的參數較多,不利于工程實現。

為此,本文針對含有不確定復合干擾的戰斗機非線性模型,提出了一種改進動態面控制方案。利用改進的一階滑模微分器估計虛擬控制信號的一階微分,避免“微分爆炸”;同時基于文獻[23]的思想提出了一種結構更簡單的干擾觀測器,對系統未知復合干擾進行估計和補償;最后通過控制分配算法得到最終控制信號。將設計的控制器用于飛機大機動仿真以驗證其有效性。

1 模型建立與問題描述

本文以某型戰斗機六自由度非線性模型為研究對象,控制目標是實現對迎角、側滑角和滾轉角的跟蹤控制,因此主要考慮姿態控制系統,數學模型如式(1)[6,10]。

(1)

式中:狀態變量x=[φαβpqrθ]T分別表示滾轉角、迎角、側滑角、滾轉角速度、俯仰角速度、偏航角速度和俯仰角,控制輸入u=[δelδerδalδarδlefδtefδr]T分別表示左右升降舵、左右副翼、前后緣襟翼和方向舵7個相互獨立的控制舵面,其余參變量含義與文獻[10]相同。

定義x1=[φ,α,β]T,x2=[p,q,r]T,x3=θ則可將模型式(1)轉換為如下形式[10]:

式中:y為系統輸出;f1(x1,x3)、f2(x)、G1(x1,x3)和G2(x)為標稱系統的向量或函數矩陣;d1(x,t)和d2(x,t)為復合干擾,d1(x,t)=Δf1+ΔG1x2+Δ1(t)、d2(x,t)=Δf2+ΔG2u+Δ2(t),式中Δf1、Δf2、ΔG1和ΔG2為系統未建模動態或飛機氣動參數攝動引起的非線性不確定部分,Δ1(t)、Δ2(t)為外部干擾。

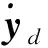
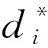
引理1[24]:對于一階滑模微分估計器:

(3)

式中:φ1、φ2和ζ1為系統狀態,h(·)為系統輸入,選擇合適的參數r1、r2和μ,則存在任意?>0,使得以下不等式成立:

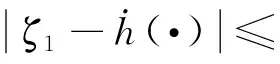
(4)

2 飛行控制器設計

2.1 控制律設計

控制律設計分為3步:1)設計虛擬控制律x2d;2)設計虛擬控制指令v;3)利用控制分配算法將虛擬控制指令v轉換為實際控制指令u。為了得到虛擬控制律x2d的微分信號,基于動態面思想,本文采用式(3)所示的一階滑模微分估計器對x2d的微分進行估計。一階滑模微分估計器基于一階滑模微分器[25]改進而來,利用雙曲正切函數代替一階滑模微分器中的符號函數,相比一階低通濾波器具有更快的收斂速度并且克服了一階滑模微分器輸出不連續的問題。

首先定義跟蹤誤差變量:

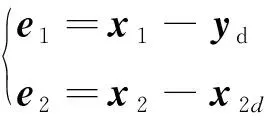
(5)

第1步:沿式(5)對e1求導得:

(6)

設計虛擬控制律x2d為:

(7)

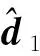
第2步:沿式(5)對e2求導,結合式(2)可得:

(8)

設計虛擬控制指令v:

(9)

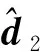
第3步:控制分配

對于多操縱面飛機而言,虛擬控制指令v的維度小于操縱面的個數。為此采用控制分配技術實現虛擬控制指令v向多操縱面飛機各個舵面的指令分配。考慮操縱面偏轉量的權值為優化指標,建立加權偽逆控制分配模型:

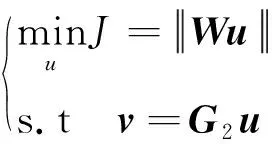
(10)

式中:W為正定對稱權值矩陣,通過合理選擇W可以協調各操縱面的偏轉量,實現舵偏范圍內的最優控制。根據最小二乘法,模型(10)的最優解為[26]:

(11)

2.2 干擾觀測器設計

飛機模型(2)中的未知復合干擾項由氣動參數攝動、未建模動態和外部干擾等多種因素引起。本文提出了一種結構簡單,物理意義明確的干擾觀測器來估計系統的未知復合干擾。

考慮如下系統:

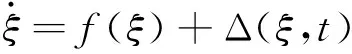
(12)

式中:Δ(ξ,t)為未知干擾,ξ為可測量的系統狀態。

定義誤差變量eξ=ξ-ξd,ξd為ξ的設計值,則有:

(13)

對上式整理可得:

(14)

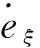
(15)

根據上述分析,為獲得d1和d2的估計值,構建如下干擾觀測器:

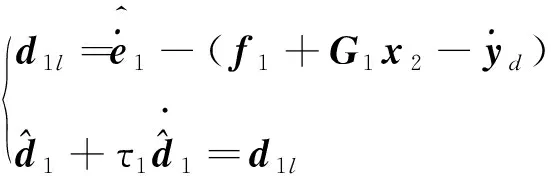
(16)

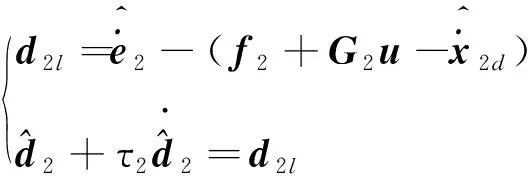
(17)

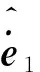
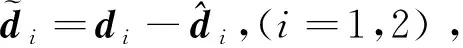
(18)

注1.之所以對d1l和d2l進行濾波,既為了得到較為平滑的控制信號,也為了避免出現“循環設計”。因為根據式(9)和(17)可以看出d2l和G20u相互耦合,利用一階低通濾波器的延遲特性可以實現兩者解耦。而將濾波器時間常數設置為遞減的變化形式,可以加快濾波器初始階段的收斂速度,并保證穩態誤差不至于過大。

3 穩定性分析

定理1.考慮由式(2)表示的飛機數學模型,在滿足假設1和2的條件下,設計基于干擾觀測器式(16)和(17)構造的虛擬控制律式(7)和(9)以及基于控制分配算法構造的實際控制律式(11),通過選擇適當的設計參數,能保證閉環系統半全局有界且使系統跟蹤誤差e1=x1-yd收斂到任意小。

證.定義Lyapunov函數:

(19)

將式(7)代入式(6),結合式(5)得:

(20)

將式(9)代入式(8)得:

(21)

對V求導得:

(22)

將式(20)和式(21)代入式(22)得:

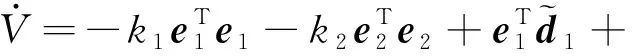
(23)

由引理1結合Young不等式得:

(24)

由式(18)結合Young不等式得:

(25)

將式(24)和式(25)代入式(23)得:

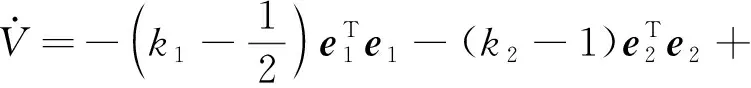
(26)

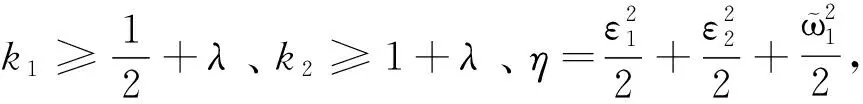
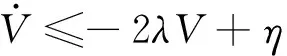
(27)

根據不變集原理[7-8],閉環系統所有信號半全局一致終結有界。

對式(27)兩邊積分得:

(28)

結合式(19)可得:

(29)

通過選擇適當的一階滑模微分估計器參數使η充分小,同時增大λ,則可使跟蹤誤差e1任意小。證畢。

4 大迎角機動仿真與分析

為驗證本文方法的有效性,利用文獻[27]中F-18戰斗機相關氣動參數取值進行仿真驗證。初始條件為:高度h=914.4m,馬赫數Ma=0.7,配平狀態的迎角和俯仰角分別為α0=3.902°,θ0=3.902°。飛機各操縱舵面最大偏轉角限定為±30°。假設飛機模型中氣動參數存在0.3sin(0.5t)的變化量,即具有30%的周期性攝動。外部干擾設置為:

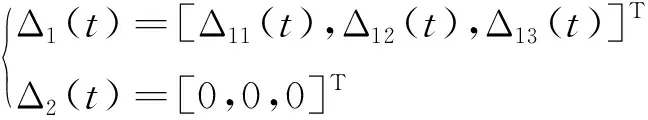
(30)

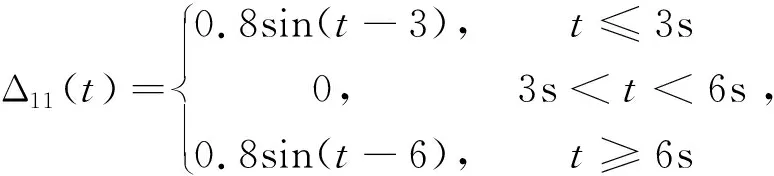
易知Δ11(t)、Δ12(t)和Δ13(t)是不可導的連續函數,所以復合干擾d1(x,t)是不可導的。

控制器參數選擇為:k1=15、k2=15,所用到的一階滑模微分估計器的參數均選擇為:r1=20、r2=1、μ=0.1,干擾觀測器參數選擇為:p=0.1、w=1、q=0.2。采用兩種方案對比仿真。

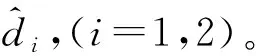
方案Ⅱ:引入本文設計的干擾觀測器對復合干擾進行補償。

由圖1～3的姿態角(迎角、側滑角、滾轉角)響應曲線可以看出,在無擾觀測器時,姿態角跟蹤誤差較大,而引入本文所設計的干擾觀測器后姿態角能迅速跟蹤參考信號,動態響應較好,跟蹤精度明顯提高,能夠理想的完成飛機大機動動作。

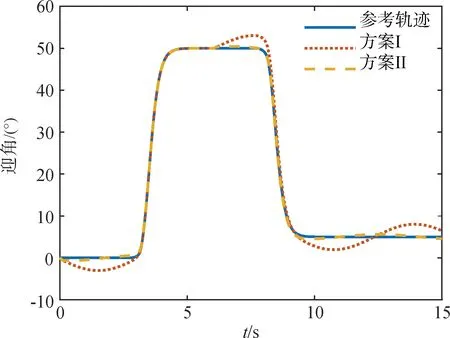
圖1 迎角響應曲線

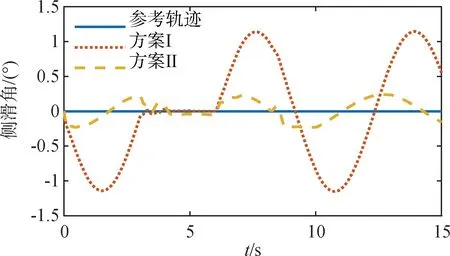
圖2 側滑角響應曲線

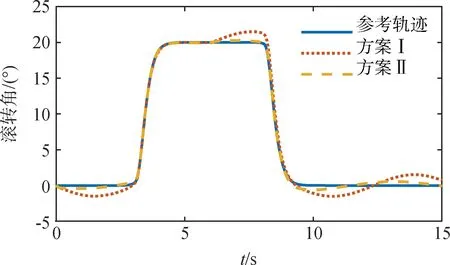
圖3 滾轉角響應曲線

5 結論

針對多操縱面戰斗機飛行控制問題,考慮模型不確定性和外部干擾的影響,設計了基于干擾觀測器的改進動態面控制方案。該方案能有效應對未知復合干擾,在氣動參數具有較大不確定性和不可導外部干擾的情況下,所設計的控制器依然能夠準確跟蹤參考信號。控制器結構簡單,易于實現,具有良好的魯棒性。