鈍體火焰穩(wěn)定器后燃燒不穩(wěn)定數(shù)值模擬
仝照旭,韓啟祥
(南京航空航天大學(xué)能源與動(dòng)力學(xué)院,南京 210016)
0 引言
隨著航空發(fā)動(dòng)機(jī)向高推重比、高可靠性的方向發(fā)展,其加力燃燒室內(nèi)部的燃燒不穩(wěn)定現(xiàn)象備受關(guān)注[1-3]。鈍體穩(wěn)定器作為最通用的火焰穩(wěn)定器之一,廣泛應(yīng)用于沖壓發(fā)動(dòng)機(jī)及渦噴發(fā)動(dòng)機(jī)加力燃燒室中[4-5]。鈍體穩(wěn)定器后燃燒不穩(wěn)定現(xiàn)象極易受來流條件的影響,隨著燃燒室來流溫度升高,來流馬赫數(shù)加大,鈍體穩(wěn)定器后發(fā)生燃燒不穩(wěn)定的幾率大幅增加,給航空發(fā)動(dòng)機(jī)高效、穩(wěn)定運(yùn)行帶來重大隱患。因此,燃燒不穩(wěn)定現(xiàn)象自從被發(fā)現(xiàn)以來,廣泛受到工程設(shè)計(jì)者的關(guān)注。但由于燃燒不穩(wěn)定現(xiàn)象受到多種因素相互作用[6-8],如化學(xué)反應(yīng),湍流流動(dòng)等,且涉及熱力學(xué)、傳熱學(xué)、聲學(xué)、流體力學(xué)等多個(gè)學(xué)科相互交叉,一直難以解決。
國內(nèi)外學(xué)者們通常采用數(shù)值模擬對(duì)燃燒不穩(wěn)定現(xiàn)象開展研究。Matthew 等[9]針對(duì)軸對(duì)稱火焰的縱向振蕩問題,采用2 維模型得到的計(jì)算結(jié)果與試驗(yàn)結(jié)果吻合程度較好,相較于3 維模型極大簡化了計(jì)算資源;劉衛(wèi)東等[10]應(yīng)用改進(jìn)的PISO 算法對(duì)液氫/液氧火箭發(fā)動(dòng)機(jī)徑向燃燒不穩(wěn)定現(xiàn)象進(jìn)行數(shù)值模擬,結(jié)果表明對(duì)該型發(fā)動(dòng)機(jī)聲腔應(yīng)用諧振器阻尼后,壓力擾動(dòng)波最終被系統(tǒng)抑制;朱旻明等[11]通過U-RANS/PDF 方法對(duì)鈍體穩(wěn)定器后漩渦脫落特性進(jìn)行分析,相對(duì)準(zhǔn)確地預(yù)測(cè)了穩(wěn)定器尾緣渦脫落頻率,但發(fā)生燃燒不穩(wěn)定時(shí)穩(wěn)定器后的局部雷諾數(shù)較高、特征時(shí)間較短(一般在μs量級(jí)),其流場具有很強(qiáng)的非定常特性及3維效應(yīng)。這些因素的限制使得國內(nèi)外關(guān)于加力燃燒室燃燒不穩(wěn)定的研究工作主要圍繞時(shí)均特征展開,導(dǎo)致對(duì)燃燒不穩(wěn)定的瞬態(tài)特征和作用機(jī)理缺乏系統(tǒng)及深入的認(rèn)識(shí)。
本文基于商用軟件Fluent,采用大渦模擬(Large Eddy Simulation,LES)方法對(duì)帶鈍體穩(wěn)定器的模型加力燃燒室進(jìn)行3 維熱態(tài)數(shù)值模擬。通過改變來流溫度、來流馬赫數(shù)、當(dāng)量比3 種影響燃燒的關(guān)鍵因素來分析其對(duì)鈍體穩(wěn)定器后燃燒不穩(wěn)定的影響。
1 研究對(duì)象與數(shù)值計(jì)算方法
1.1 幾何模型
選擇加力燃燒室中常見的鈍體穩(wěn)定器,尺寸如圖1 所示。其主要參數(shù)為:槽寬D=45 mm、頂角α=30°、頂角半徑R=12 mm、壁厚b=3mm。大渦模擬對(duì)網(wǎng)格精度和計(jì)算資源要求極高,有必要對(duì)計(jì)算域進(jìn)行簡化。本文采用Euqenio[12]對(duì)帶鈍體穩(wěn)定器的模型燃燒室進(jìn)行簡化:對(duì)鈍體高度方向取45 mm(1D),簡化后鈍體高度方向2 個(gè)面取平移周期邊界,3維計(jì)算域如圖2所示。
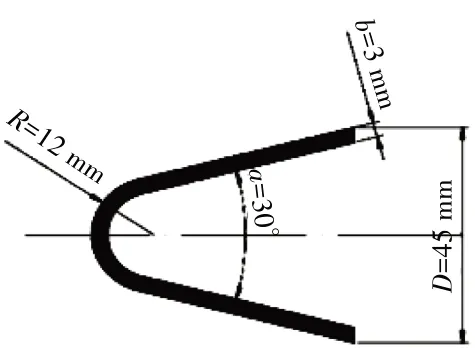
圖1 鈍體穩(wěn)定器尺寸
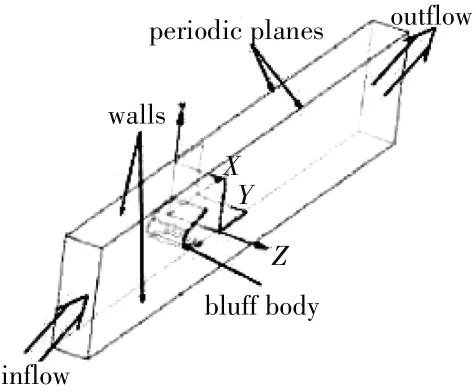
圖2 3維計(jì)算域
計(jì)算域在笛卡爾坐標(biāo)下表示,選取鈍體穩(wěn)定器尾緣中心為原點(diǎn),x方向?yàn)殚L度方向,y方向?yàn)閷挾确较颍瑉方向?yàn)楦叨确较颉? 維計(jì)算域尺寸為750 mm×136 mm×45 mm。
1.2 網(wǎng)格劃分與獨(dú)立性驗(yàn)證
采用ICEM 軟件劃分計(jì)算域結(jié)構(gòu)化網(wǎng)格。為了精準(zhǔn)捕捉鈍體穩(wěn)定器壁面的流動(dòng)分離現(xiàn)象,對(duì)其周圍劃分邊界層網(wǎng)格,鈍體穩(wěn)定器壁面第1 層網(wǎng)格高度Δy≤0.02 mm,邊界層網(wǎng)格增長率為1.2,滿足LES 對(duì)于近壁網(wǎng)格的要求(y+~1)。整體網(wǎng)格劃分從鈍體穩(wěn)定器出發(fā),向周圍均勻過渡。網(wǎng)格總體質(zhì)量≥0.85,網(wǎng)格最小正交性≥0.7。
對(duì)冷態(tài)流場選取3種數(shù)量的網(wǎng)格進(jìn)行無關(guān)性驗(yàn)證:mesh1(41.8萬)、mesh2(117.2萬)、mesh3(240.1萬)。3種網(wǎng)格穩(wěn)定器尾緣x=15 mm處時(shí)均流向速度如圖3所示。從圖中可見,當(dāng)網(wǎng)格量從117.2萬增大到240.1萬時(shí),由于網(wǎng)格量改變?cè)斐傻挠?jì)算誤差基本可以忽略,綜合求解精度以及計(jì)算成本選取117.2萬(mesh2)進(jìn)行數(shù)值計(jì)算。中心截面網(wǎng)格剖分如圖4所示。
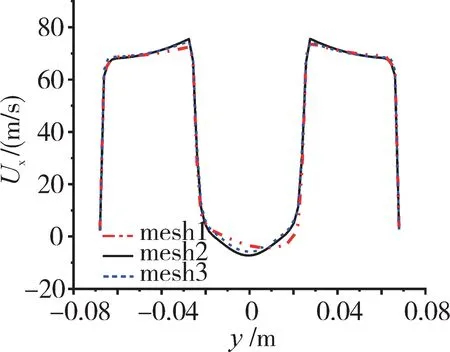
圖3 3種網(wǎng)格穩(wěn)定器尾緣x=15 mm處流向時(shí)均速度

圖4 中心截面網(wǎng)格剖分
1.3 計(jì)算模型與算例驗(yàn)證
1.3.1 計(jì)算模型
湍流模型選擇LES 模型,其中亞格子模型選擇Wale 模型。因?yàn)閃ale 模型是一種類似Smagorinsky模型的代數(shù)模型,但克服了Smagorinsky 模型耗散偏大的缺陷且能夠相對(duì)準(zhǔn)確地預(yù)測(cè)層流到湍流的過渡。
離散相模型選擇非穩(wěn)態(tài)顆粒追蹤,離散相顆粒選擇適合液體燃料的液滴(Droplet),阻力系數(shù)Cd選擇動(dòng)力學(xué)曳力模型(Dynamic Drag Model)。離散相模型普適性好,幾乎適用所有的流動(dòng)情形,二次霧化選擇波動(dòng)破碎模型(Wave Break Up),噴嘴類型選擇實(shí)心噴嘴(Solid Cone)。
在鈍體穩(wěn)定器前150 mm 處垂直來流方向設(shè)置6 個(gè)噴嘴來提供燃燒所需的燃料,供油位置(黑色圓圈)如圖5所示。

圖5 供油位置
燃燒模型選取有限速率/渦耗散模型(Finite-Rate/Eddy-Dissipation,F(xiàn)R/ED),該模型結(jié)合了Arrhenius 公式和渦耗散方程,避免了Eddy-Dissipation 模型出現(xiàn)的提前燃燒問題,并且結(jié)合了動(dòng)力學(xué)因素和湍流因素,廣泛用于航空發(fā)動(dòng)機(jī)燃燒室的燃燒模擬。采用航空煤油2步總包反應(yīng)[13]。
本文采用有限體積法求解納維-斯托克斯方程(Navier-Stokes,N-S)方程,壓力和速度耦合采用SIMPLE 算法,壓力項(xiàng)采用2 階迎風(fēng)格式,動(dòng)量項(xiàng)采用中心差分格式,時(shí)間離散采用中心差分格式。為保證計(jì)算精度,時(shí)間步長選取1×10-6s。
1.3.2 標(biāo)準(zhǔn)算例驗(yàn)證
本文通過標(biāo)準(zhǔn)算例來驗(yàn)證選擇的計(jì)算模型能否準(zhǔn)確預(yù)測(cè)穩(wěn)定器后的流場、氣流的脈動(dòng)頻率以及火焰的分布形態(tài)。其中Giacomazzi 等[12]和Fureby[14]的研究對(duì)象為閉口鈍體穩(wěn)定器,Barry 等[15]的研究對(duì)象為開口鈍體穩(wěn)定器。
1.3.2.1 穩(wěn)定器后流場結(jié)構(gòu)對(duì)比
本文與Giacomazzi 的模擬結(jié)果的對(duì)比如圖6 所示。從圖中可見,二者在穩(wěn)定器后流域的漩渦數(shù)量均為6個(gè)。從左向右前3個(gè)漩渦在流域中的位置幾乎一致,后3 個(gè)漩渦的空間分布稍有差異,但總體分布位置相似。故本文的計(jì)算方法可以相對(duì)準(zhǔn)確地預(yù)測(cè)鈍體穩(wěn)定器后的流場結(jié)構(gòu)。
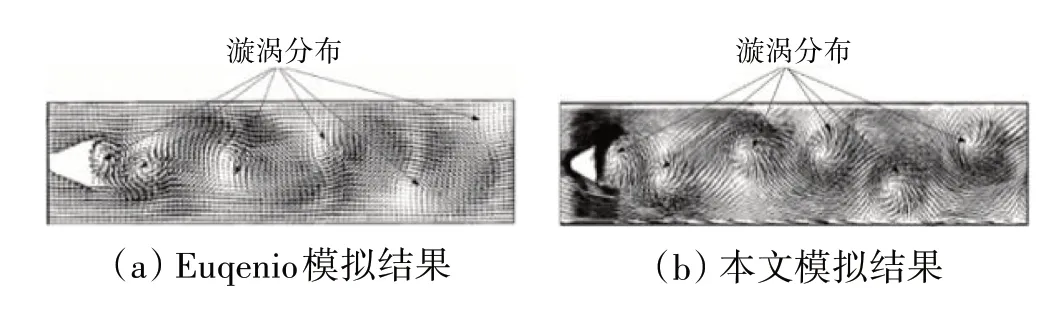
圖6 本文與Euqenio模擬結(jié)果的對(duì)比
1.3.2.2 穩(wěn)定器后監(jiān)測(cè)點(diǎn)的脈動(dòng)頻率
穩(wěn)定器后監(jiān)測(cè)點(diǎn)脈動(dòng)頻率見表1。從表中可見,本文的計(jì)算結(jié)果與Fureby的試驗(yàn)結(jié)果的誤差為5.7%,且 與Giacomazzi 的模擬結(jié)果的誤差相差較小。說明本文的計(jì)算方法可以相對(duì)準(zhǔn)確地預(yù)測(cè)鈍體穩(wěn)定器后氣流的脈動(dòng)頻率。
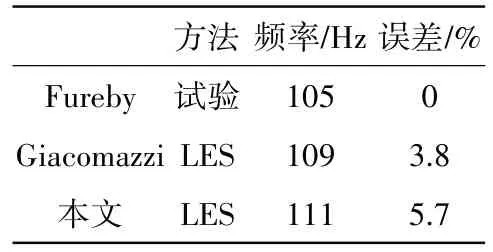
表1 穩(wěn)定器后監(jiān)測(cè)點(diǎn)脈動(dòng)頻率
1.3.2.3 穩(wěn)定器后火焰形態(tài)
鈍體穩(wěn)定器尾跡火焰形態(tài)如圖7 所示。從圖中可見,本文的模擬結(jié)果與Barry 等[15]通過高速攝影得到的穩(wěn)定器后火焰形態(tài)的一致性較好。
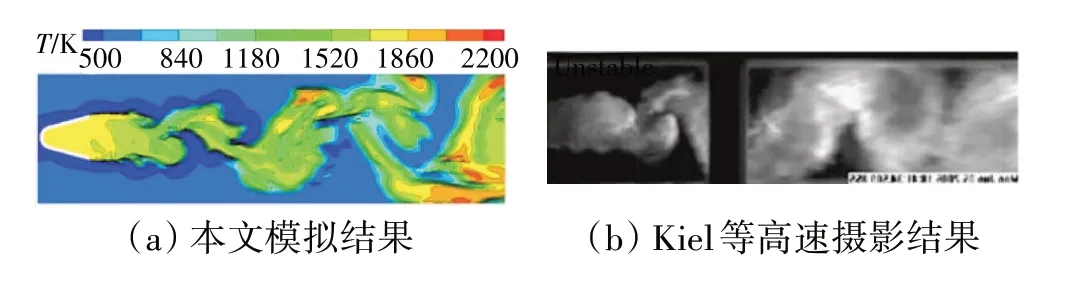
圖7 鈍體穩(wěn)定器尾跡火焰形態(tài)
1.4 物性參數(shù)與邊界條件
計(jì)算域中流體介質(zhì)為空氣或者航空煤油多組分混合物。介質(zhì)的物性參數(shù)設(shè)置包括密度、定壓比熱容cp、動(dòng)力粘度μ和導(dǎo)熱系數(shù)λ。對(duì)于空氣分別采用分段多項(xiàng)式(Piecewise-polynomial)、Sutherland 公式、動(dòng)力學(xué)理論(Kinetic-theory)進(jìn)行計(jì)算;對(duì)于混合物采用混合定律計(jì)算;對(duì)于密度項(xiàng)ρ均選擇理想不可壓縮氣體。
邊界條件:采用速度進(jìn)口、壓力出口,壁面采用固壁無滑移邊界,展向2個(gè)表面采用平移周期邊界。
2 穩(wěn)定器后燃燒不穩(wěn)定的影響因素
給出本文的基準(zhǔn)參數(shù),然后在此基礎(chǔ)上對(duì)部分參數(shù)進(jìn)行修改來研究鈍體穩(wěn)定器后燃燒不穩(wěn)定的影響因素。
基準(zhǔn)參數(shù)為:速度進(jìn)口:Ma=0.1,900 K;壓力出口:0.1 MPa;當(dāng)量比:0.76。
在穩(wěn)定器后中心截面沿流向方向設(shè)置5 個(gè)監(jiān)測(cè)點(diǎn)用于分析燃燒室下游火焰的脈動(dòng)情況。其流向坐標(biāo)分別為:point-1(x=0.01 m)、point-2(x=0.05 m)、point-3(x=0.10 m)、point-4(x=0.20 m)、point-5(x=0.30 m)。監(jiān)測(cè)點(diǎn)位置如圖8所示。
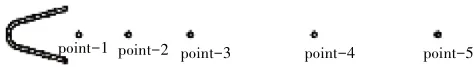
圖8 監(jiān)測(cè)點(diǎn)位置
2.1 來流溫度的影響
通常情況下,加力燃燒室的進(jìn)口即是主燃燒室的出口,進(jìn)入加力燃燒室的氣體為經(jīng)過主燃燒室燃燒并經(jīng)過渦輪膨脹作功后的高溫混氣。相較于主燃燒室來說,加力燃燒室來流混氣含氧量較低,燃燒條件相對(duì)較差,但從另一角度看,隨著來流溫度的升高,混氣含氧量雖然降低,但溫度提高對(duì)燃燒有利。選擇3 種來流溫度600、900、1200 K,分析來流溫度變化對(duì)鈍體穩(wěn)定器后燃燒不穩(wěn)定的影響。
通過簡單的熱力學(xué)分析[16]估算主燃燒室燃燒后的混氣溫度與混氣成分之間的關(guān)系(假設(shè)燃油完全燃燒),計(jì)算得到的結(jié)果見表2。
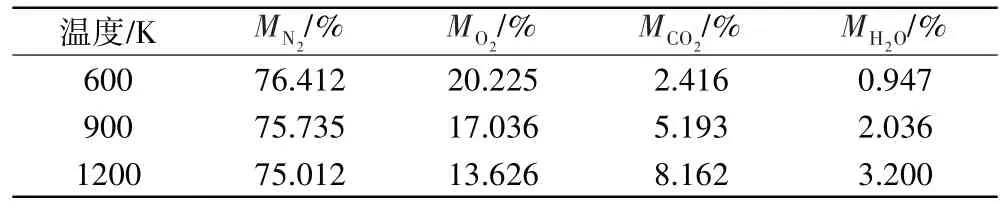
表2 不同溫度時(shí)來流氣體成分的質(zhì)量分?jǐn)?shù)
不同來流溫度時(shí)鈍體穩(wěn)定器后溫度分布如圖9所示。從圖中可見,不同來流溫度對(duì)應(yīng)鈍體穩(wěn)定器后火焰形態(tài)差異較大。當(dāng)來流溫度為600 K 時(shí),穩(wěn)定器后的火焰近似呈直線狀,燃燒不穩(wěn)定性主要體現(xiàn)在內(nèi)部火焰與外部混氣的交界處,整個(gè)交界處呈波浪形火焰,但此時(shí)火焰面還未出現(xiàn)大尺度旋渦,穩(wěn)定器尾部火焰幾乎完全呈現(xiàn)K-H 不穩(wěn)定;當(dāng)來流溫度為900 K時(shí),火焰形態(tài)由2 部分組成:穩(wěn)定器尾緣向后延伸一小段長度的剪切層火焰,在剪切層火焰后原本的直線狀火焰逐漸變?yōu)橛葿VK 不穩(wěn)定主導(dǎo)的旋渦火焰;當(dāng)來流氣體溫度達(dá)到1200 K 時(shí),穩(wěn)定器尾部火焰幾乎完全呈現(xiàn)由BVK 不穩(wěn)定主導(dǎo)的旋渦火焰,并且燃燒室下游火焰的擺動(dòng)幅度很大。
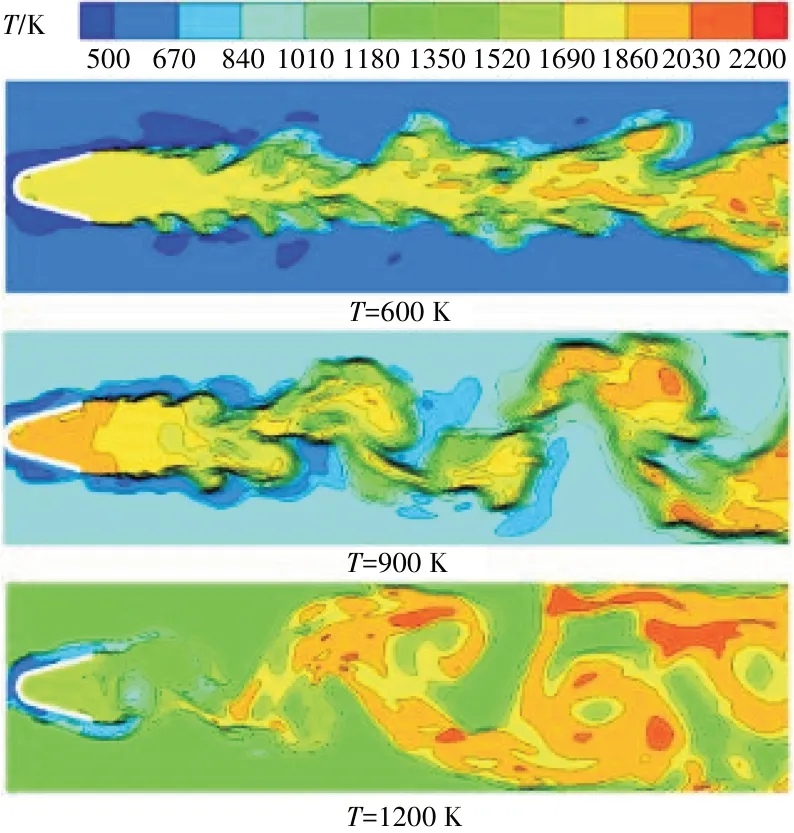
圖9 不同來流溫度時(shí)鈍體穩(wěn)定器后溫度分布
通過上述分析可知,來流溫度是影響穩(wěn)定器后火焰形態(tài)的1 個(gè)重要因素。其深層原因之一是由于未氣化的液態(tài)煤油不易改變方向,因此在來流溫度較低時(shí),低溫油霧“包裹”在鈍體穩(wěn)定器后火焰表面抑制其向旋渦火焰轉(zhuǎn)變;而當(dāng)來流溫度較高時(shí),液態(tài)煤油會(huì)被高溫來流氣體加熱而迅速氣化,僅有少部分未來得及氣化的低溫油霧順著穩(wěn)定器兩側(cè)向下游流去,但很快就完全氣化。因此在來流溫度較高時(shí),剪切層火焰向旋渦火焰轉(zhuǎn)變的流向位置會(huì)提前。Gokulakrishnan等[17]同樣以相似結(jié)構(gòu)的鈍體穩(wěn)定器為研究對(duì)象,選擇丙烷為燃料在來流溫度為600 K 時(shí)穩(wěn)定器后火焰形態(tài)與本文以液體煤油為燃料、來流溫度為900 K 時(shí)的類似。
不同來流溫度時(shí)鈍體穩(wěn)定器后速度分布如圖10所示。從圖中可見,穩(wěn)定器后火焰由K-H 不穩(wěn)定主導(dǎo)時(shí),穩(wěn)定器后流場速度分布分層較為明顯。高速區(qū)主要集中在火焰與壁面之間,低速區(qū)主要集中在穩(wěn)定器尾緣;而當(dāng)火焰由K-H 不穩(wěn)定向BVK 不穩(wěn)定轉(zhuǎn)變時(shí),穩(wěn)定器后非對(duì)稱漩渦將極大影響流場中速度分布,從中心截面的瞬時(shí)速度分布可見,當(dāng)BVK 不穩(wěn)定出現(xiàn)后,在穩(wěn)定器下游產(chǎn)生速度很高的渦團(tuán),使得原本相對(duì)規(guī)則的速度分布變得不均勻。
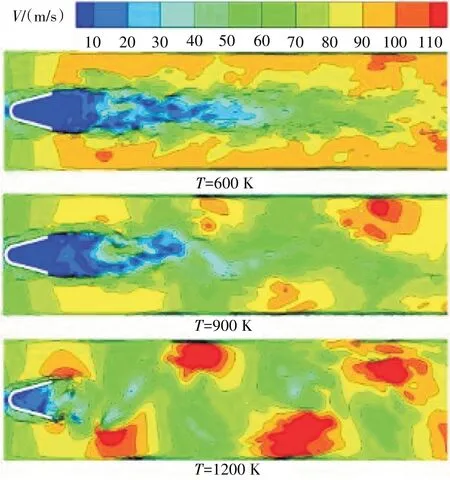
圖10 不同來流溫度時(shí)鈍體穩(wěn)定器后速度分布
2.2 來流馬赫數(shù)的影響
來流馬赫數(shù)通過影響湍流流動(dòng)、油氣混合、油氣駐留時(shí)間等因素,進(jìn)而影響鈍體穩(wěn)定器后火焰的燃燒不穩(wěn)定現(xiàn)象。分別選取來流馬赫數(shù)Ma=0.1、0.2、0.3,分析來流馬赫數(shù)變化對(duì)穩(wěn)定器后燃燒不穩(wěn)定的影響。
不同來流馬赫數(shù)時(shí)鈍體穩(wěn)定器后溫度分布如圖11 所示。從圖中可見,從整體上看,3 種來流馬赫數(shù)時(shí)穩(wěn)定器后火焰形態(tài)非常接近,穩(wěn)定器后幾乎完全由BVK 不穩(wěn)定主導(dǎo)的旋渦火焰占據(jù),表明來流馬赫數(shù)對(duì)穩(wěn)定器后的火焰形態(tài)影響較小。但從細(xì)節(jié)上看,當(dāng)來流馬赫數(shù)較低時(shí),穩(wěn)定器后火焰面較為光滑,沒有出現(xiàn)大量褶皺;而隨著來流馬赫數(shù)逐漸提高,火焰面逐漸凹凸不平,越來越多的褶皺出現(xiàn)在火焰表面。表明隨著來流馬赫數(shù)提高,穩(wěn)定器后的火焰表面趨于破碎。由于燃油從霧化、蒸發(fā)需要一定時(shí)間,隨著來流馬赫數(shù)提高,低溫燃油在燃燒室的駐留時(shí)間縮短。當(dāng)馬赫數(shù)為0.1 時(shí),穩(wěn)定器尾緣低溫燃油(圖中藍(lán)色區(qū)域)基本消耗殆盡;而當(dāng)來流馬赫數(shù)提高到0.2 時(shí),少量低溫燃油出現(xiàn)在燃燒室中部;當(dāng)來流馬赫數(shù)達(dá)到0.3時(shí),甚至在燃燒室下游也有低溫燃油的存在。
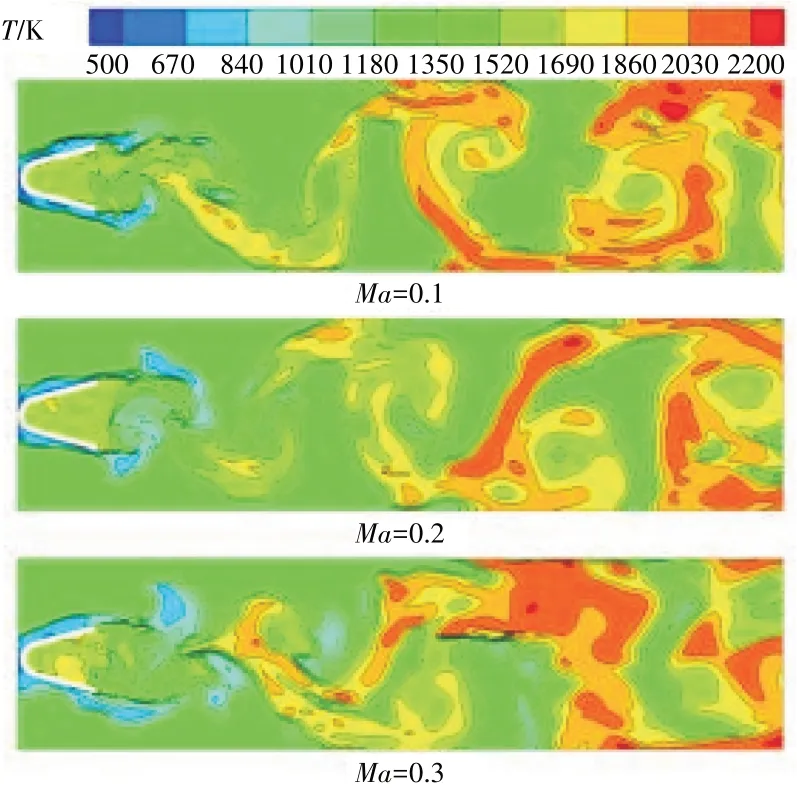
圖11 不同來流馬赫數(shù)時(shí)鈍體穩(wěn)定器后溫度分布
由于來流馬赫數(shù)不同,不能把三者的速度標(biāo)尺設(shè)為一致。將3 種工況下速度標(biāo)尺的上限設(shè)置為各自來流馬赫數(shù)的2 倍,比較3 種來流馬赫數(shù)時(shí)鈍體穩(wěn)定器后速度分布的變化。
不同來流馬赫數(shù)時(shí)鈍體穩(wěn)定器后的速度分布如圖12所示。從圖中可見,從整體上看,三者的速度分布相似,這與溫度分布的結(jié)果趨于一致。表明在由相同火焰不穩(wěn)定性主導(dǎo)的區(qū)域具有相近的溫度分布以及速度分布。但從細(xì)節(jié)上看,在低來流馬赫數(shù)時(shí),穩(wěn)定器后方的渦團(tuán)較為完整,尺寸較大且各渦團(tuán)之間尺度相近;隨著來流馬赫數(shù)提高,穩(wěn)定器后大尺度的渦團(tuán)在高速氣流的沖擊下逐漸破碎成次級(jí)尺度渦團(tuán)。
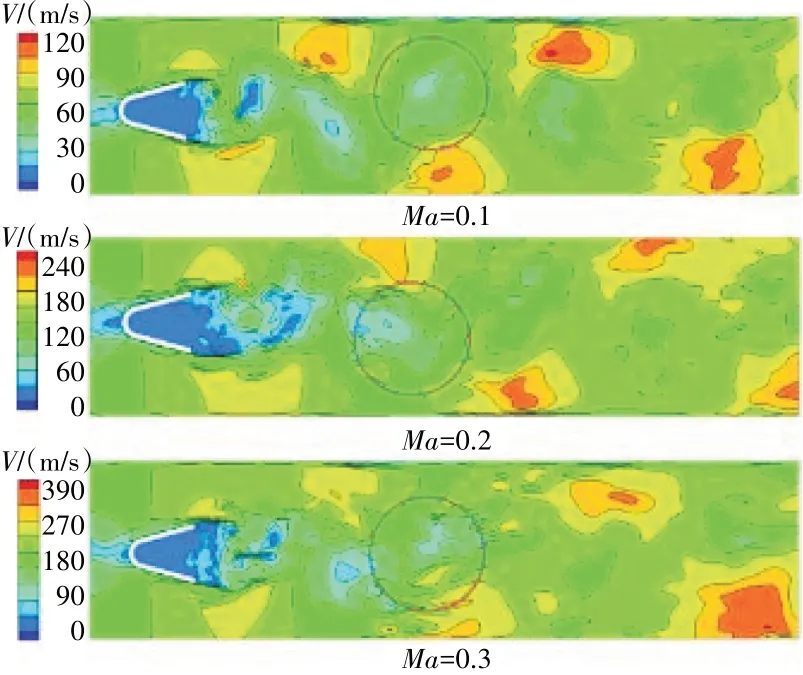
圖12 不同來流馬赫數(shù)時(shí)鈍體穩(wěn)定器后速度分布
為了分析鈍體穩(wěn)定器后火焰的脈動(dòng)特征,設(shè)置監(jiān)測(cè)點(diǎn)(圖7)。以來流馬赫數(shù)為0.3、監(jiān)測(cè)點(diǎn)5 為例。將該點(diǎn)壓力脈動(dòng)與放熱脈動(dòng)的時(shí)域圖和頻域圖進(jìn)行整理,如圖13所示。
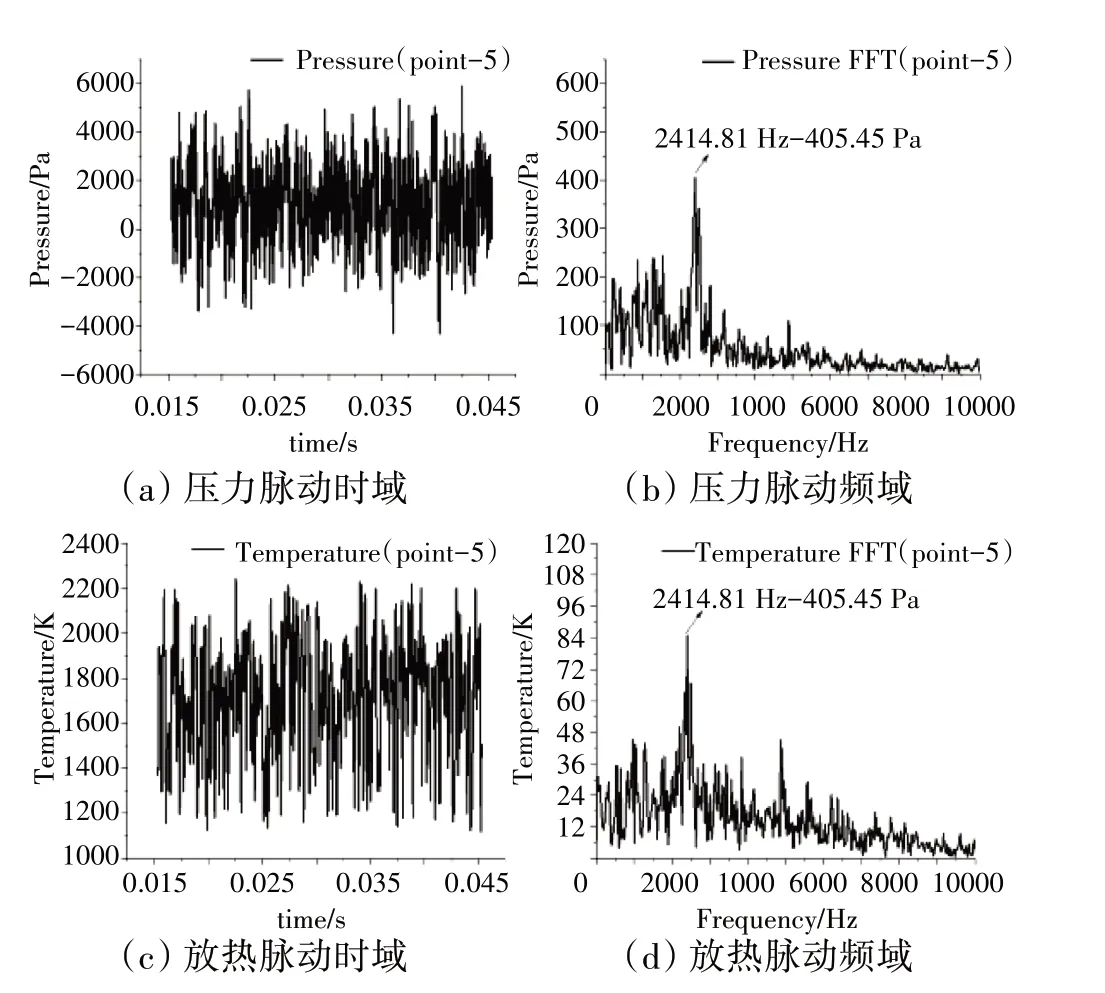
圖13 監(jiān)測(cè)點(diǎn)5壓力脈動(dòng)與放熱脈動(dòng)時(shí)域與頻域
從圖13(a)、(c)中可見,無論是壓力脈動(dòng)還是放熱脈動(dòng),時(shí)域曲線均充滿毛刺,表明流場中除了大尺度渦以外還存在小尺度渦。對(duì)應(yīng)到圖13(b)、(d)上可得,頻域曲線除了主頻外,還存在很多與主頻振幅可比的次頻。
將3 種工況下鈍體穩(wěn)定器后監(jiān)測(cè)點(diǎn)的時(shí)域曲線進(jìn)行FFT 變換得到火焰壓力脈動(dòng)和放熱脈動(dòng)的頻譜信息,分別如圖14、15所示。
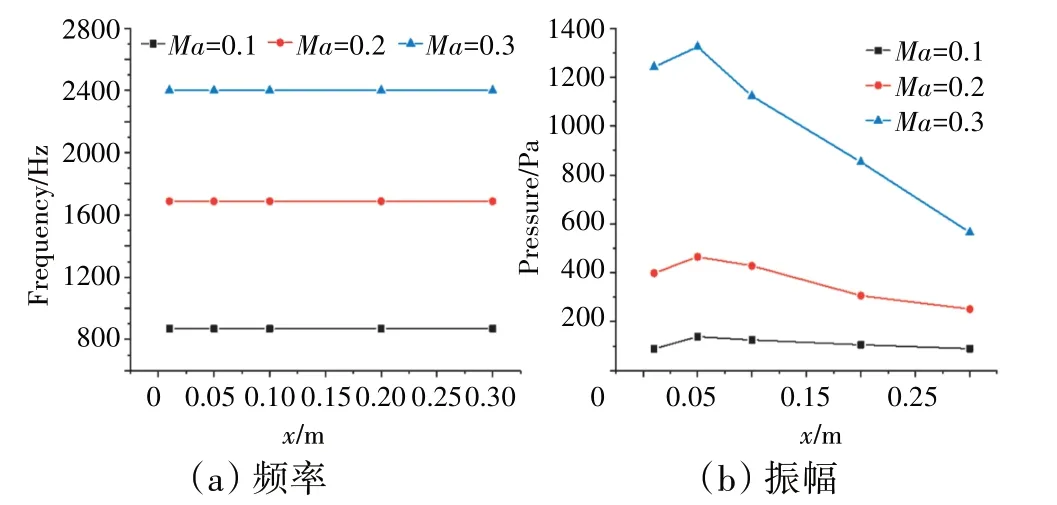
圖14 不同來流馬赫數(shù)時(shí)監(jiān)測(cè)點(diǎn)壓力脈動(dòng)頻域
從圖14 中可見,隨著來流馬赫數(shù)提高,燃燒不穩(wěn)定的壓力脈動(dòng)頻率呈提高趨勢(shì)。這是由于提升來流馬赫數(shù)會(huì)加快穩(wěn)定器尾緣非對(duì)稱旋渦的生成,而這些非對(duì)稱漩渦會(huì)對(duì)穩(wěn)定器下游流場產(chǎn)生顯著影響。壓力脈動(dòng)的振幅同樣隨著來流馬赫數(shù)的提高而增大,這可以解釋為提高來流馬赫數(shù)會(huì)導(dǎo)致流場中各處的平均流速提高,進(jìn)而導(dǎo)致氣流壓力脈動(dòng)更劇烈。
對(duì)比圖14(a)和圖15(a)可見,發(fā)生燃燒不穩(wěn)定現(xiàn)象時(shí),火焰的放熱脈動(dòng)和壓力脈動(dòng)的頻率較為接近,這是因?yàn)榉艧崦}動(dòng)和壓力脈動(dòng)均會(huì)受流場中大尺度旋渦的影響。從圖15(b)中可見,一方面,當(dāng)來流馬赫數(shù)從0.1提高到0.2時(shí),放熱脈動(dòng)的幅值呈增大趨勢(shì),這是因?yàn)檫m當(dāng)提高來流馬赫數(shù)使得穩(wěn)定器下游油滴破碎程度更大,霧化效果更好。另一方面,當(dāng)馬赫數(shù)從0.2 提高到0.3 時(shí),放熱脈動(dòng)幅值反而在3 種來流馬赫數(shù)下最小。這可以解釋為當(dāng)來流馬赫數(shù)過高時(shí),盡管對(duì)穩(wěn)定器后油霧破碎和混合有利,但同時(shí)減少了油氣混合的時(shí)間和油霧在燃燒室的駐留時(shí)間,且過快的氣流會(huì)將燃燒不穩(wěn)定產(chǎn)生的熱量過早帶出燃燒室,不利于熱量的累積。
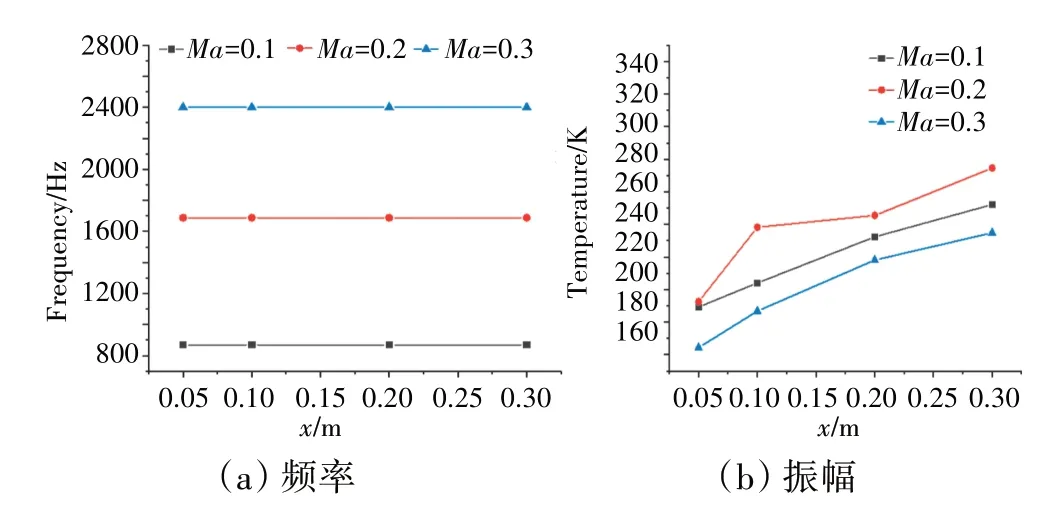
圖15 不同來流馬赫數(shù)時(shí)監(jiān)測(cè)點(diǎn)放熱脈動(dòng)頻域
2.3 當(dāng)量比的影響
鈍體穩(wěn)定器后的燃燒不穩(wěn)定現(xiàn)象與當(dāng)量比密切相關(guān)。選取當(dāng)量比為0.5、0.6、0.7,分別當(dāng)量比變化對(duì)穩(wěn)定器后燃燒不穩(wěn)定的影響。
不同當(dāng)量比時(shí)鈍體穩(wěn)定器后溫度分布如圖16 所示。從圖中可見,在不同當(dāng)量比時(shí)鈍體穩(wěn)定器后火焰形態(tài)趨于一致,均為剪切層火焰和旋渦火焰共存,2種火焰形態(tài)的過渡位置在流向方向位置也幾乎一致。表明當(dāng)量比從0.5增大到0.7時(shí),不會(huì)對(duì)穩(wěn)定器尾部火焰形態(tài)造成顯著影響。
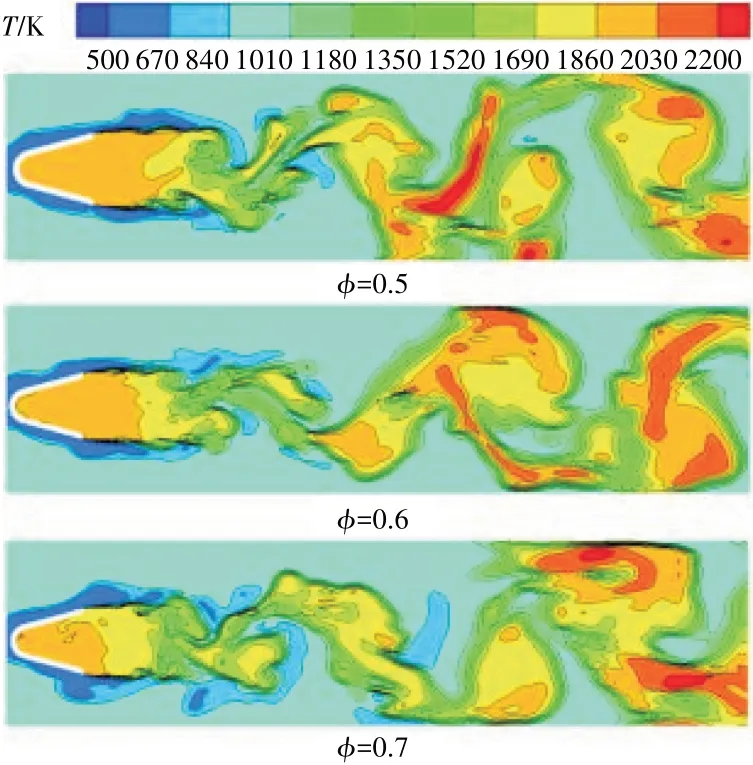
圖16 不同當(dāng)量比時(shí)鈍體穩(wěn)定器后溫度分布
不同當(dāng)量比時(shí)鈍體穩(wěn)定器后速度分布如圖17 所示。從圖中可見,從整體上看,3 種當(dāng)量比時(shí)穩(wěn)定器后速度分布基本一致,均在穩(wěn)定器外側(cè)形成速度梯度,在穩(wěn)定器尾緣形成一定范圍的低速區(qū),且在低速區(qū)尾部出現(xiàn)K-H 不穩(wěn)定與BVK 不穩(wěn)定的過渡;但從細(xì)節(jié)來看,當(dāng)量比為0.5 時(shí)Φ= 0.5,在BVK 主導(dǎo)的旋渦火焰區(qū)域出現(xiàn)尺寸較大的圓形或橢圓形的渦團(tuán);而當(dāng)量比為0.6Φ= 0.6 時(shí),這些渦團(tuán)被拉伸,形狀呈條狀;隨著當(dāng)量比增大到為0.7Φ=0.7時(shí),被拉伸的渦團(tuán)破碎成更小尺度的渦團(tuán)。表明隨著當(dāng)量比的增大,燃燒室下游的燃燒情況更為復(fù)雜,其中的火焰尺度更廣。
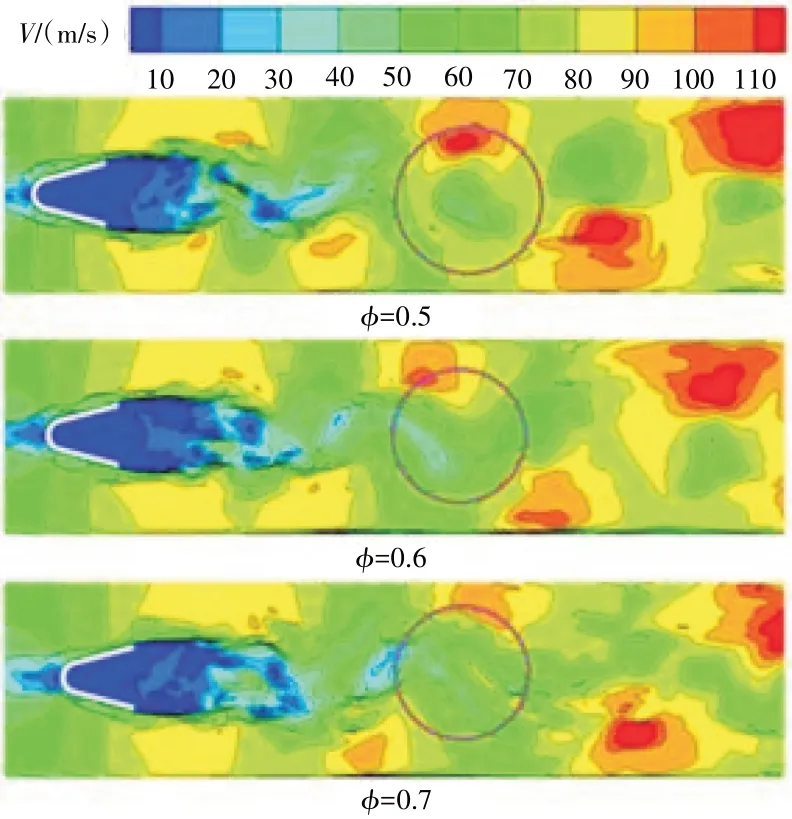
圖17 不同當(dāng)量比時(shí)鈍體穩(wěn)定器后速度分布
不同當(dāng)量比時(shí)監(jiān)測(cè)點(diǎn)壓力脈動(dòng)和放熱脈動(dòng)的頻域如圖18、19 所示。從圖中可見,隨著當(dāng)量比從0.5增大到0.7,火焰的脈動(dòng)頻率變化較小,表明在一定范圍內(nèi)火焰的脈動(dòng)頻率對(duì)當(dāng)量比并不敏感。隨著當(dāng)量比從0.5 增大到0.6,壓力脈動(dòng)的幅值對(duì)應(yīng)增大,而當(dāng)量比從0.6 增大到0.7,壓力脈動(dòng)幅值卻不增反減;放熱脈動(dòng)的幅值變化趨勢(shì)與之基本相同。這可以解釋為穩(wěn)定器后存在1 個(gè)局部最佳當(dāng)量比,在當(dāng)量比小于局部最佳當(dāng)量比時(shí),增大供油量會(huì)加快化學(xué)反應(yīng)速率,提高燃燒室內(nèi)平均溫度;而當(dāng)量比大于局部最佳當(dāng)量比時(shí),再增大供油量將會(huì)使穩(wěn)定器后局部富油,過量的低溫油霧不僅會(huì)抑制火焰燃燒而且使得燃燒室下游平均溫度降低。
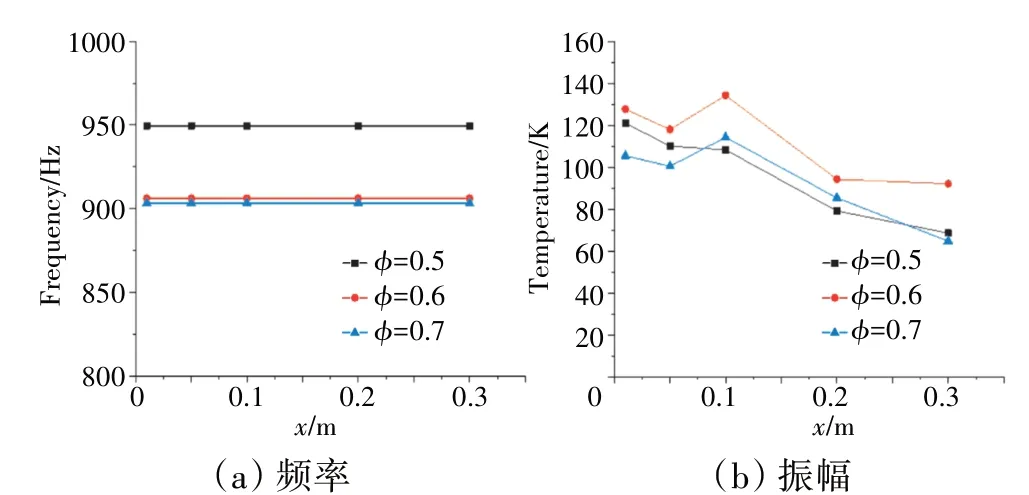
圖18 不同當(dāng)量比時(shí)監(jiān)測(cè)點(diǎn)壓力脈動(dòng)頻域
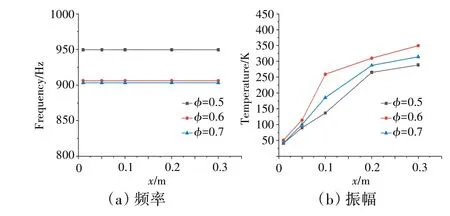
圖19 不同當(dāng)量比時(shí)監(jiān)測(cè)點(diǎn)放熱脈動(dòng)頻域
本文選擇的FR/ED 模型只能用于單步或雙步反應(yīng),對(duì)于湍流燃燒的細(xì)節(jié)刻畫較為粗糙。根據(jù)Porumbel 等[18]的觀點(diǎn):FR/ED 模型容易高估反應(yīng)區(qū)的厚度,采用該模型計(jì)算得到剪切層火焰的長度與厚度可能偏高,這可能是導(dǎo)致當(dāng)量比改變時(shí)穩(wěn)定器后火焰形態(tài)變化較小的一種原因。但同時(shí)Porumbel也指出,在穩(wěn)定器下游由于燃燒過程化學(xué)能的添加使FR/ED 模型在遠(yuǎn)離穩(wěn)定器的區(qū)域的預(yù)測(cè)能力有所提升。
3 結(jié)論
(1)來流溫度對(duì)穩(wěn)定器后火焰形態(tài)有顯著影響。當(dāng)來流溫度為600 K 時(shí),穩(wěn)定器后火焰形態(tài)由K-H 不穩(wěn)定主導(dǎo);而當(dāng)來流溫度升到高900 K 時(shí),K-H 不穩(wěn)定與BVK 不穩(wěn)定共存;當(dāng)來流溫度達(dá)到1200 K 時(shí),穩(wěn)定器后火焰形態(tài)由BVK不穩(wěn)定主導(dǎo)。
(2)來流馬赫數(shù)對(duì)穩(wěn)定器后火焰形態(tài)影響較小;提升來流馬赫數(shù)會(huì)顯著提高火焰的脈動(dòng)頻率,并且壓力脈動(dòng)的幅值也有同樣的變化趨勢(shì)。但提升來流馬赫數(shù)會(huì)對(duì)燃燒產(chǎn)生2 種相反的影響:一方面,提高來流馬赫數(shù)會(huì)使得燃油破碎更好,油霧混合更充分,有利于燃燒;另一方面過高的來流馬赫數(shù)使得油霧的駐留時(shí)間縮短,并且將燃燒產(chǎn)生的熱量迅速帶走,對(duì)火焰的放熱脈動(dòng)產(chǎn)生不利影響。
(3)燃油當(dāng)量比從0.5增大到0.7時(shí)穩(wěn)定器后火焰形態(tài)變化較小。穩(wěn)定器后存在局部最佳當(dāng)量比。當(dāng)超過局部最佳當(dāng)量比時(shí)繼續(xù)增大供油量,局部富油會(huì)抑制火焰的放熱脈動(dòng)。

