基于法蘭同軸測試原理的織物屏蔽效能仿真

孫娜 徐陽

摘要： 為了在設計階段更好地預測和評價織物的屏蔽性能，文章采用CST微波工作室建立了基于法蘭同軸測試原理的織物屏蔽效能仿真模型，分析了電磁屏蔽織物兩種等效模型的適用范圍，并通過織物屏蔽效能測試驗證了仿真的準確性。結果表明：仿真模型能夠模擬法蘭同軸裝置對試樣屏蔽效能的測試過程;網格模型可作為鍍銀長絲織物的仿真等效模型，且當織物中紗線截面短軸尺寸小于0.05 mm、孔徑率小于0.30時，織物結構可簡化為平板模型;不同嵌織比、不同層數的鍍銀長絲嵌織織物屏蔽效能測試結果與仿真結果在數值和變化趨勢上基本一致，平均誤差在6%以內，證明采用此仿真模型預測鍍銀長絲織物屏蔽效能是可行的。

關鍵詞： 法蘭同軸法;鍍銀長絲織物;電磁屏蔽織物;織物模型;電磁仿真;屏蔽效能

中圖分類號： TS101.8

文獻標志碼： A

文章編號： 1001-7003（2023）05-0052-07

引用頁碼： 051107

DOI： 10.3969/j.issn.1001-7003.2023.05.007

基金項目：

中央高校基本科研業務費專項資金項目（JUSRP52007A）

作者簡介：

孫娜（1997），女，碩士研究生，研究方向為功能紡織品。通信作者：徐陽，教授，zh3212@vip.sina.com。

電磁屏蔽織物具有柔軟、質輕、強度高等優點，被認為是一種理想的屏蔽材料，廣泛應用于電磁兼容和電磁防護等領域［1］。衡量電磁屏蔽織物屏蔽效果的重要指標——屏蔽效能（SE），目前主要通過實驗測試獲得。但由于織物的柔軟性和手工操作的偶然性，使得測試結果不穩定，極大地干擾了織物屏蔽性能的測量;此外測試只能在織物生產后進行，設計周期長、實驗成本高［2］。為了在織物設計階段可以預測其屏蔽性能，進而開發出屏蔽效能好、成本低的電磁屏蔽織物，研究科學有效的仿真方法以預測和評價織物的屏蔽性能成為當前的研究重點。

目前織物屏蔽效能的仿真主要基于屏蔽室法測試原理，通過仿真軟件定義織物組織單元周期邊界條件，使電場和磁場在樣品平面互相垂直分布，從而實現1～18 GHz高頻織物結構參數等因素對屏蔽效能影響的分析［3-5］。但由于屏蔽室法測試成本高、對測試技能要求嚴格，故而在實際生產和研究中多采用設備成臺性好、操作簡單的法蘭同軸法［9］。與屏蔽室法不同，法蘭同軸法是針對0.03～1.50 GHz的遠場電磁環境測試方法，且電磁場在樣品平面的分布更為復雜，因此兩者對織物屏蔽效能的測試會存在明顯差異［6］。目前尚無基于法蘭同軸法的織物屏蔽效能仿真方式。為了更好指導實際生產和研究，本文基于法蘭同軸法屏蔽效能的測試原理，采用CST軟件建立織物屏蔽效能仿真模型，探討電磁屏蔽織物等效模型的適用范圍，并通過不同嵌織比、不同層數的鍍銀長絲織物屏蔽效能測試實驗，驗證仿真模型的有效性。

1 初始模型建立

1.1 同軸測試原理

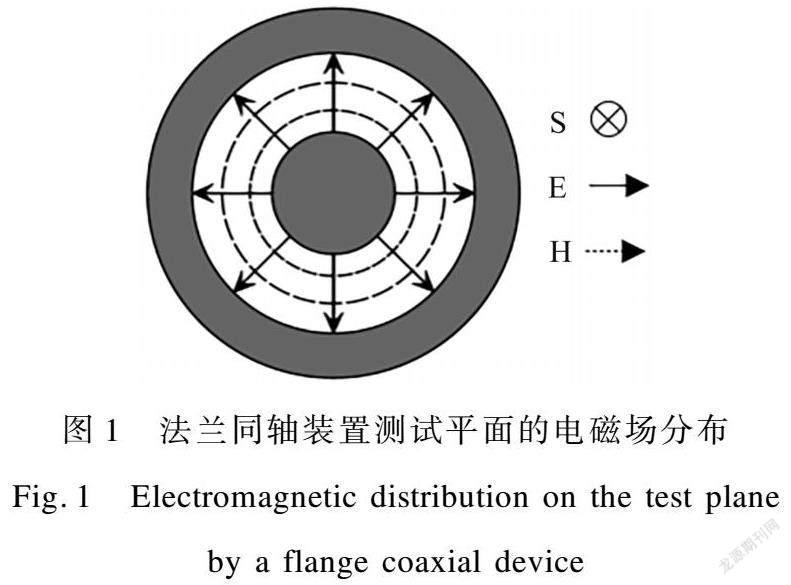
法蘭同軸測試技術基于同軸傳輸線傳輸主模橫電磁波的原理，由于導體的趨膚效應，電磁波通過同軸夾具的內外導體傳播，在樣品平面分布如圖1所示（S為電磁波傳播方向、E為電場向量、H為磁場向量）［7］。測試時，在同軸間夾持待測材料，可以模擬遠場環境中材料對電磁波的屏蔽效能測試過程。

1.2 同軸測試裝置模型建立

法蘭同軸測試裝置結構如圖2所示，其中同軸測試夾具包括左右對稱且特性阻抗均為50 Ω的同軸線，2個同軸接口分別連接信號源和信號接收機，兩測試夾具之間放置待測屏蔽材料，屏蔽材料厚度需小于最高測量頻率波長的1%，即厚度不超過2 mm。

使用CST微波工作室按照標準GJB 6190—2008《電磁屏蔽材料屏蔽效能測量方法》中給出的法蘭同軸裝置的實際尺寸建立三維模型，為了仿真方便，忽略法蘭結構，將測試裝置的左右兩部分通過內外導體直接連接。在此基礎上，增加測量夾具使其滿足不同厚度材料的放置，夾具由內外導體兩部分組成，尺寸與同軸內外導體尺寸一致，作為法蘭同軸的延續體可以在保持同軸良好密封性的同時防止電磁波泄漏，使仿真結果更為準確［8］。同軸裝置仿真模型如圖3所示，模型內外導體及夾具材料設置為理想導體（PEC），支撐介質材料為聚四氟乙烯（PTFE）。由于電磁波只在內、外導體之間的空腔內傳播，因此可以認為結構被嵌入理想導體內部，故設置邊界條件為電邊界（等效于理想導體，電場垂直于邊界表面）、并在同軸接口兩端定義激勵端口，阻抗均為50 Ω，以使能量能夠進入和離開理想導體。為了確認同軸測試裝置的傳輸性能，根據圖3模型，采用頻域求解器分別在無試樣、負載導電試樣（電導率1 000 S/m、厚度0.1 mm）情況下進行仿真。

在無試樣、負載試樣情況下，1 GHz時同軸傳輸線內電流分布及測試平面的場分布如圖4所示。當負載高導電試樣時，輸入的電磁波被試樣反射、吸收，幾乎未透過試樣，且輸出的電磁波強度較無試樣負載時顯著降低。同時測試平面電場由圓心沿著半徑方向傳播，磁場沿著平行于圓周的同心圓環分布，與實際測試中試樣表面場分布（圖1）情況一致，說明該仿真模型能夠模擬法蘭同軸裝置對試樣屏蔽效能的測試過程。模型仿真的準確性取決于裝置的反射情況，通常采用電壓駐波比VSWR。

傳輸線上相鄰的波腹點與波谷點電壓振幅之比，其值越接近1，說明裝置的反射越小、仿真結果越準確。圖5為無試樣負載時裝置的電壓駐波比結果，可以看出在0.03～1.50 GHz頻段，VSWR<1.2，可視為電磁波在同軸裝置中無損傳輸，符合標準中對測試用法蘭同軸的技術要求。

2 織物模型構建與分析

2.1 織物模型構建

圖6（a）所示的電磁屏蔽機織物由經、緯兩個方向的鍍銀長絲交織而成，在織物中形成了交叉處連通的導電網絡，具有典型的網格結構，而紗線交織處的孔洞對電磁波幾乎無屏蔽作用，因此織物的有效屏蔽結構為導電網格結構，故可以將導電網格結構作為鍍銀長絲電磁屏蔽織物的等效模型進行理論計算和仿真［9-10］。織物網格模型如圖6（b）所示，鍍銀長絲截面被簡化為理想矩形。

式中：k為孔徑率，d、t分別為截面長軸和短軸尺寸，w為相鄰紗線間距。

但當相鄰紗線的間距較小時，其耦合作用導致電磁屏蔽織物沒有出現明顯的電磁泄漏，呈現出與無孔隙的平板材料相近的屏蔽效能，且電磁泄漏與孔徑大小、深度直接相關［11］。因此，當織物孔徑率小于某一臨界值時不會顯著影響其屏蔽效能，織物結構可簡化為平板模型，即孔徑率k=0的無孔金屬板結構。

平板模型較網格模型結構更加規則，網格劃分相對簡單，因此將織物結構簡化為平板模型進行仿真可極大提高計算速度，但需明確模型的適用范圍，以確保仿真結果的準確性。

2.2 織物模型的適用范圍分析

織物中鍍銀長絲規格（長軸、短軸）的變化會改變模型孔徑大小和深度，影響對電磁波的傳輸與衰減，進而影響織物模型的適用性。在實際應用中，鍍銀長絲直徑取決于基體長絲（如滌綸、錦綸長絲）直徑，其直徑大多分布在0.05～050 mm［12］。同時，結合紗線在織物中被壓扁這一實際情況，考慮了織物中紗線壓扁系數0.65～0.80，最終定義紗線短軸尺寸t在0.03～0.50 mm、長軸尺寸d在0.08～0.80 mm。

在CST中利用Brick（立方體）工具建立不同紗線規格、不同孔徑率的網格結構模型，定義網格電導率為1.59×105 S/m，將其夾持在測試夾具之間。按照1.2對仿真條件進行設置，最后采用頻域求解器進行求解計算，得到不同紗線規格下屏蔽效能隨孔徑率k變化的仿真結果，如圖7所示。

由圖7可知，當t≤0.05 mm時，d=0.1、0.5、0.8 mm的導電網格屏蔽效能均隨k值增大而減小，且在整個孔徑率范圍內（0～1）可以根據曲線拐點k′分為2個階段：第一階段，當k≤k′時，由于相鄰導電紗之間的耦合效應較強，通過孔隙的電磁泄漏并不大，所以不同孔徑率下的導電網格屏蔽效能基本一致，且與孔徑率為0的平板結構屏蔽效能近似相等;第二階段，當k＞k′時，電磁泄漏帶來的衰減效應逐漸增加，屏蔽效能隨孔隙率增大而下降。圖7中k′點孔徑率約為0.3，故可取0.3為臨界孔徑率。仿真中，當織物孔徑率低于0.3時，織物模型可簡化為平板模型;高于0.3，織物模型則采用網格模型。

當t＞0.05 mm時，孔徑率k為0.1～0.4的不同長軸尺寸導電網格屏蔽效能均高于k=0的導電平板屏蔽效能，此時除了相鄰導電紗之間的較強耦合作用外，孔徑深度的增加也使孔的波導效應隨之增大，波導衰減貢獻的屏蔽效能SEwg見下式［13］。

式中：c為真空中的光速，m/s;f為入射波頻率，Hz;t為孔徑深度，m;a為孔徑大小，m。

由式（3）可知，當孔徑深度較大且孔徑尺寸較小時，波導衰減的影響不能忽略，使較小孔徑率的導電網格屏蔽效能在相同厚度的導電平板基礎上有所增加，故此時臨界孔徑率不存在，織物屏蔽效能的仿真等效模型僅為網格結構模型。

因此在選擇織物模型時，只需考慮織物中紗線的短軸尺寸，當t≤0.05 mm時，可取0.3為臨界孔徑率，根據織物實際孔徑率選擇平板模型或網格模型。

3 織物屏蔽效能仿真與分析

為了驗證基于法蘭同軸測試原理的織物屏蔽效能仿真模型對不同織物結構的兼容性，本文考慮了嵌織間距和織物層數兩個因素，選用電導率為1.59×105 S/m的滌綸基鍍銀長絲織物，建立等效模型，并導入同軸裝置仿真模型對其屏蔽效能進行計算。織物幾何結構參數如表1所示。

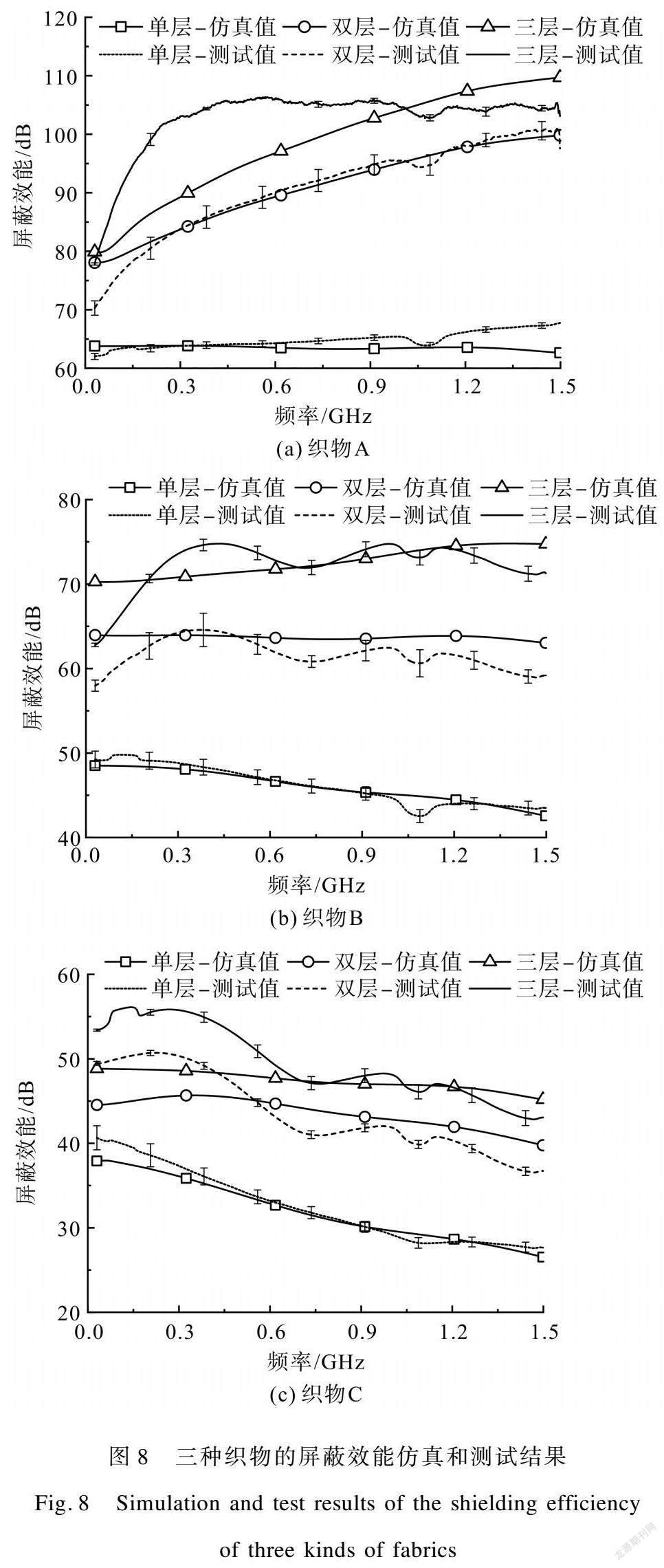
本文參考GJB 6190—2008，采用法蘭同軸裝置測試織物在0.03～1.50 GHz頻率的屏蔽效能，為了提高測試的準確性、減小誤差，對每種織物選取3塊不同位置的試樣并分別測試5次，取其平均值。圖8為仿真計算值與實際屏蔽效能對比結果。

由圖8可知，三種織物的實測屏蔽效能與仿真結果在數值和變化趨勢上基本一致，平均誤差在6%以內，并且誤差隨著層數和嵌織間距的增加而增大。誤差的主要原因有以下三方面：一是對織物模型的簡化處理，忽視了織物中紗線的屈曲波高，減少了織物內部導電紗線的含量。二是模型認為導電紗線各節點之間接觸良好（接觸電阻為0），而實際存在一定的接觸電阻。但在兩者綜合作用下，三種織物的單層實測屏蔽效能與仿真結果誤差較小，同時隨著層數增加，導電紗線含量帶來的影響增大，誤差也逐漸增大。三是多層織物的疊放位置差異，仿真中織物模型緊密接觸且層間導電網格彼此對齊;而在實驗中由于織物的柔軟性和疊放的緊密程度差異使得織物之間存在一定間隙，層數越多，產生間隙的可能性越大。另外手工操作不免使層間導電網格交錯、互相導通，且導電紗線嵌織間距越大，網格間的交錯、導通對其屏蔽效能影響越大，因此最大誤差發生在織物層數為3層、鍍銀長絲/滌綸1︰8嵌織時。

對比圖8中的數據可以發現，不同嵌織間距、不同層數電磁屏蔽織物的屏蔽效能隨頻率增大呈現出不同的變化趨勢：在單層織物中，織物A的屏蔽效能趨于穩定，而織物B、C呈下降趨勢，因為隨著織物中鍍銀長絲嵌織間距的增大，所形成的導電網格孔徑率增大，因此在較高頻率時電磁波對織物的穿透增加，屏蔽效能的下降幅度增加;在多層織物中，由于織物層數的增加，層間孔隙相互遮擋，限制了電磁波的直接通路，減少了電磁波在高頻時的穿透，同時材料整體厚度增大、吸收損耗提高，且吸收損耗與頻率正相關，因此織物A、B的屏蔽效能隨電磁波頻率增大而增大。而織物C孔徑率過大，織物層間孔隙遮擋效果不明顯，因此其屏蔽效能仍呈下降趨勢，但下降幅度明顯減小。

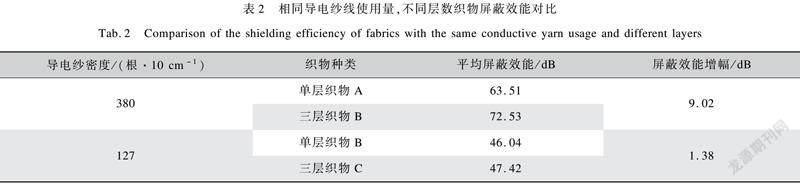
不同層數織物屏蔽效能的仿真和測試結果清晰地表明，隨著層數增加織物屏蔽效能隨之增加，但屏蔽效能的提高率逐漸降低，同時層數增加意味著導電紗線使用量增加、生產成本提高。為了進一步分析相同導電紗線使用量情況下，織物層數對屏蔽效能的影響，本文以恒定的導電紗線使用量為基準，比較了單層織物A和三層織物B、單層織物B和三層織物C的屏蔽效能仿真結果，如表2所示，仿真中三層織物B、C交錯疊放，使相鄰導電紗間距分別與織物A、B相同，以消除孔徑率的影響。由表2可知，在相同導電紗線使用量情況下，增加織物層數可以在一定程度上提高其屏蔽效能，這是由于導電紗線沿電磁波傳播方向的分布增加后，增大了材料內部的吸收損耗和多次反射衰減，因此屏蔽效能提高。同時導電紗線含量越大，層數增加帶來的屏蔽效能增幅越顯著。

4 結 論

本文基于法蘭同軸法屏蔽效能測試原理，通過CST微波工作室建立了0.03～1.50 GHz頻段織物屏蔽效能的仿真模型，解決了僅依靠設備測試容易產生較大誤差和成本的問題。在此基礎上，分析了電磁屏蔽織物的兩種等效模型的適用范圍，并對鍍銀長絲織物的屏蔽效能進行仿真，得到以下結論：

1） 織物屏蔽效能仿真計算中，采用導電網格結構作為鍍銀長絲織物的仿真等效模型，但當紗線截面短軸尺寸小于0.05 mm且孔徑率小于0.3時，織物結構可簡化為平板結構。

2） 不同嵌織比、不同層數的鍍銀長絲織物的屏蔽效能仿真和測試結果均具有較好的一致性，驗證了仿真模型對不同鍍銀長絲織物結構的兼容性。

3） 在相同導電紗線使用量情況下，增加織物層數可以提高其屏蔽效能，同時導電紗線含量越大，層數增加帶來的屏蔽效能增幅越顯著。

最后，由于本文僅以鍍銀長絲織物為例，對于使用該方法預測織物屏蔽性能是否具有普適性，還有待進一步論證。

參考文獻：

［1］閆鑫鑫， 謝春萍， 劉新金， 等. 不銹鋼纖維機織物的電磁屏蔽及力學性能［J］. 絲綢， 2018， 55（8）： 29-34.

YAN Xinxin， XIE Chunping， LIU Xinjin， et al. Electromagnetic shielding and mechanical properties of stainless steel fiber woven fabrics［J］. Journal of Silk， 2018， 55（8）： 29-34.

［2］LIU Z， WANG X C. FDTD numerical calculation of shielding effectiveness of electromagnetic shielding fabric based on warp and weft weave points［J］. IEEE Transactions on Electromagnetic Compatibility， 2020， 62（5）： 1693-1702.

［3］孫天， 張一曲， 趙曉明， 等. 緯編針織物電磁屏蔽效能CST仿真分析［J］. 材料導報， 2019， 33（18）： 3130-3134.

SUN Tian， ZHANG Yiqu， ZHAO Xiaoming， et al. CST simulation analysis of electromagnetic shielding effectiveness of weft-knitted fabric［J］. Materials Reports， 2019， 33（18）： 3130-3134.

［4］李建雄， 賈紅玉， 陳純鍇， 等. 基于各向異性織物的電磁屏蔽性能仿真計算［J］. 材料導報， 2018， 32（18）： 3235-3238.

LI Jianxiong， JIA Hongyu， CHEN Chunkai， et al. Simulation of electromagnetic shielding performance based on anisotropic fabric［J］. Materials Reports， 2018， 32（18）： 3235-3238.

［5］蘇欽城， 趙曉明， 李衛斌， 等. 基于有限積分法的機織物電磁屏蔽效能仿真分析［J］. 紡織學報， 2016， 37（2）： 155-160.

SU Qincheng， ZHAO Xiaoming， LI Weibin， et al. Simulation analysis of woven fabric electromagnetic shielding effectiveness using finite integration technique［J］. Journal of Textile Research， 2016， 37（2）： 155-160.

［6］肖紅， 唐章宏， 施楣梧， 等. 織物屏蔽效能的法蘭同軸法和屏蔽室法測試對比研究［J］. 紡織學報， 2016， 37（3）： 47-54.

XIAO Hong， TANG Zhanghong， SHI Meiwu， et al. Comparative research on electromagnetic shielding effectiveness of fabric tested by flange coaxial method and shielding chamber method［J］. Journal of Textile Research， 2016， 37（3）： 47-54.

［7］陳超嬋， 繆軼， 朱建剛， 等. 電磁屏蔽薄膜屏蔽效能的測量裝置［J］. 上海計量測試， 2018， 45（3）： 24-27.

CHEN Chaochan， MIU Yi， ZHU Jiangang， et al. Development on measurement tester of electromagnetic shielding effectiveness for electromagnetic shielding film［J］. Shanghai Measurement and Testing， 2018， 45（3）： 24-27.

［8］李美英. 屏蔽效能測量方法和一種屏蔽材料機理的研究［D］. 北京： 北京交通大學， 2021.

LI Meiying. Study on the Measurement of Shielding Effectiveness and the Mechanism of a Shielding Material［D］. Beijing： Beijing Jiaotong University， 2021.

［9］肖紅， 施楣梧， 鈔杉， 等. 機織物有效結構模型的電磁屏蔽效能影響因素［J］. 紡織學報， 2015， 36（7）： 42-49.

XIAO Hong， SHI Meiwu， CHAO Shan， et al. Influential factors of electromagnetic shielding effectiveness based on effective woven fabrics structure model［J］. Journal of Textile Research， 2015， 36（7）： 42-49.

［10］GHIDA A A， LIONE P， LAURENT D， et al. Effective electromagnetic properties of woven fiber composites for shielding applications［J］. IEEE Transactions on Electromagnetic Compatibility， 2020， 62（4）： 1082-1089.

［11］關福旺， 肖紅， 施楣梧， 等. 織物基頻率選擇表面材料的制備及應用［J］. 紡織學報， 2016， 37（2）： 141-148.

GUAN Fuwang， XIAO Hong， SHI Meiwu， et al. Fabrication and application of fabric based frequency selective surface［J］. Journal of Textile Research， 2016， 37（2）： 141-148.

［12］徐克平. 鍍銀纖維織物的防電磁輻射性能研究［D］. 天津： 天津工業大學， 2012.

XU Keping. Study on Electromagnetic Radiation Resistance of Silver-Coated Fabric［D］. Tianjin： Tiangong University， 2012.

［13］白婉欣. 周期開孔導體板的電磁屏蔽效能研究［D］. 北京： 華北電力大學， 2020.

BAI Wanxin. Research on Electromagnefic Shielding Effectiveness of the Conductor Plate with Periodic Apertures［D］. Beijing： North China Electric Power University， 2020.

Abstract： With the rapid development of information technology， the application of electronic equipment in communication， transportation， finance and other fields increases rapidly， resulting in increasingly severe electromagnetic environment in space. The electromagnetic shielding material is one of the main means to deal with the threat of electromagnetic environment. Among the commonly used electromagnetic shielding materials， the electromagnetic shielding fabric has been widely used because of its characteristics of softness， light weight and high strength. In the development process of the electromagnetic shielding fabric， the development cycle is long because of the complex fabric structure and many influencing factors. In addition， due to the softness of the fabric and the chance of manual operation， the test results will be unstable. Meanwhile， the test and evaluation of the shielding efficiency can only be carried out after the production of the fabric， which further increases the design cycle and experiment cost of the electromagnetic shielding fabric. Therefore， it has become a research hotspot to use scientific and effective simulation methods to predict the shielding efficiency in fabric design stage.

In order to guide the actual production and research， we developed a fabric shielding efficiency simulation method in the frequency range of 0.03-1.50 GHz， aiming at the testing method of flange coaxial fabric shielding efficiency with good platform performance and simple operation. Firstly， the structure model of the flange-coaxial device was constructed by CST microwave studio. Combined with the shielding efficiency test principle of the flange-coaxial method， simulation parameters were set and preliminary simulation was carried out to confirm the transmission performance of the device. Then， two equivalent models of the electromagnetic shielding fabric were established and their application range was analyzed. Finally， the shielding efficiency of silver-coated filament fabrics with different interweave spacing and layers was calculated by simulation， and the accuracy of the simulation was verified by fabric shielding efficiency tests. The results show that the simulation model can simulate the testing process of the shielding efficiency of the flange coaxial device. The mesh model can be used as the simulation equivalent model of the silver-coated filament fabric， and the fabric structure can be simplified into a flat plate model when the short axis size of the yarn section is less than 0.05 mm and the aperture ratio is less than 0.30. The test results of shielding efficiency of the silver-coated filament woven fabric with different embedding ratios and different layers are basically consistent with the simulation results， and the average error is less than 6%， which proves that the simulation model is feasible to predict the shielding efficiency of the silver-coated filament woven fabric.

In this paper， a fabric shielding efficiency simulation model based on the flange coaxial test principle is established， and it can quickly calculate the shielding efficiency of the silver-coated filament electromagnetic shielding fabric， shorten the experimental period and reduce the experimental cost for the design of this kind of electromagnetic shielding fabric. However， as the types of electromagnetic shielding fabrics also include surface metallized fabrics， metal fiber blended fabrics and conductive nonmetallic fabrics， this paper only takes silver-coated filament fabrics as an example. Whether this simulation model can be used to predict the shielding effectiveness of other types of electromagnetic fabrics needs further demonstration.

Key words： flange coaxial method; silver-coated filament fabric; electromagnetic shielding fabric; fabric model; electromagnetic simulation; shielding efficiency